Cím: Szabályos ötszög szerkesztése vonalzóval és hosszátvivővel
Szerző(k):  Strommer Gyula 
Füzet: 1989/szeptember, 245 - 249. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

D. Hilbert 1899-ben a göttingai Gauss-Weber emlékmű leleplezése alkalmából megjelent ,,Grundlagen der Geometrie'' c. híres ünnepi iratában mellesleg azokkal a szerkesztésekkel is foglalkozott, amelyek megoldásához a vonalzón kívül csak hosszátvivő, vagyis oly eszköz kell, amely tetszés szerinti vonaldaraboknak egyik egyenesről tetszés szerinti más egyenesre való átrakását teszi lehetővé, * és megmutatta, hogy minden körzővel és vonalzóval megszerkeszthető szabályos sokszög vonalzóval és hosszátvivővel is megszerkeszthető kell, hogy legyen.
A következőkben a szabályos ötszög vonalzóval és hosszátvivővel való szerkesztését mutatjuk meg.
Evégből először néhány szerkesztési alapfeladatot kell vonalzóval és hosszátvivővel megoldanunk. E feladatok a következők:

 

1. feladat. Húzzunk adott ponton át adott egyenessel párhuzamos egyenest.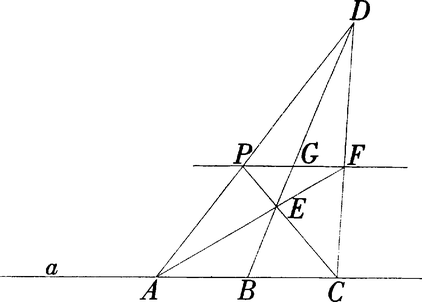
 

 
 
1. ábra
 

Megoldás: Kössük össze az adott P pontot az adott a egyenes tetszés szerinti A pontjával (1. ábra) és mérjük rá az adott egyenesre az egymással egyenlő AB és BC távolságot. Vegyünk fel AP meghosszabbításán egy D pontot és kössük össze B-vel és C-vel. Ha a CP egyenes BD-t E-ben és az AE egyenes CD-t F-ben metszi, akkor PF lesz a keresett egyenes.
Valóban, ha a BD,CD és AE egyenesek a P ponton át a-val párhuzamosan rajzolt egyenest a G,F és F' pontban metszik, akkor
PG:GF=AB:BC
és
PG:GF'=BC:AB=AB:BC,
amiből következik, hogy az F és F' pontok egybeesnek, s így a P-ből a-val párhuzamosan húzott egyenes átmegy AE és CD metszéspontján.
2. feladat. Rajzoljunk adott egyenesre merőleges egyenest.
 

Megoldás: Mérjük rá az adott egyenesre, annak egy tetszés szerinti A pontjától mindkét irányban az egymással egyenlő AB és AC távolságot (2. ábra), azután határozzuk meg az A ponton átmenő másik két egyenesen, AB-nek ugyanazon oldalán, a D és E pontokat úgy, hogy AD=AE=AB legyen. Akkor a BD és CE egyenesek metszik egymást egy F pontban, a BE és CD egyenesek pedig egy M pontban és az FM egyenes merőleges 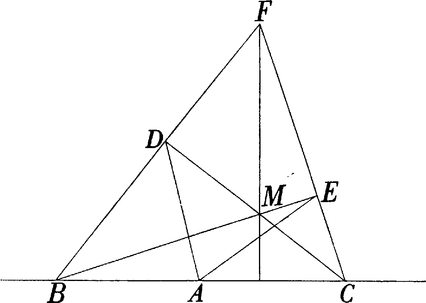AB-re.
 
 
2. ábra
 

Valóban, a BDC∢ és BEC∢, mint a BC fölé írt félkörben az átmérőn nyugvó kerületi szög, derékszög. Ennélfogva M a BCF háromszög magasságpontja, és így FM merőleges BC-re.
 
E két feladat alapján könnyen lehet adott egyenesre, ennek adott pontjában merőlegest emelni és adott egyenesre kívüle fekvő ponton át merőlegest szerkeszteni, s így távolságot is felezni.
Térjünk át ezek után a szabályos ötszög megszerkesztésére. E végből tekintsük az egységnyi oldalú szabályos tíz szöget (3. ábra), melynek csúcsait a 0, 1, 2, ..., 9 számokkal jelöljük. Az 51, 14, 42 átlók a tízszög egyik felét négy háromszögre osztják.
 
 
3. ábra
 

Az ábrán feltüntettük e háromszögek szögeinek 180∘:10=18∘-ra mint szögegységre vonatkozó mérőszámait. Ha a négy háromszöget úgy helyezzük egymásra, hogy ezen szögük szárai egybeessenek, akkor a 145, 412 és 243 háromszögeknek a közös szöggel szemben fekvő oldalai a 015 derékszögű háromszöget négy egyenlő szárú háromszögre osztják, melyeknek szárai egységnyi hosszúságúak. E háromszögek alapját az ábrán látható módon x1,x2,x3 és x4-gyel jelöljük. Az x1 és x4 alapú háromszöget az alaphoz tartozó magassága olyan derékszögű háromszögekre osztja, melyeknek átfogója egységnyi hosszúságú, egyik szöge 18∘, e szög mellett fekvő befogója x1, és a vele szemben fekvő befogója x4 felével egyenlő; az x4 alapú háromszög magassága tehát x1 felével egyenlő, és viszont. Hasonló módon láthatjuk be, hogy az x3 alapú háromszög magassága x2 felével egyenlő és viszont. Az ábra alapján továbbá
1:12x1=x1:(1+12x2),
azaz
x12=2+x2;
hasonló módon:

1:12x1=x2:12(x1+x3),x1x2=x1+x3;1:12x1=x3:12(x2+x4),x1x3=x2+x4;...x1:(1+12x2)=x2:12(x1+x3)x22=x12+x1x3-2x2=2+x4;....

Ily módon a következő szorzótáblát kapjuk:
x1   x2   x3x4x1   2+x2   x1+x3   x2+x4   x3x2   x1+x3   2+x4   x1   x2-x4x3   x2+x4   x1   2-x4   x1-x3x4   x3   x2-x4   x1-x3   2-x2   

 

Az x2 és x4 alapú háromszögekből összeállítható a 4. ábrán látható egyenlő szárú háromszög, amelyből
1+x4=x2
és így
x2-x4=1.

 
 
4. ábra
 

A szorzótáblából pedig
x2x4=x2-x4=1.

Így a másodfokú egyenlet gyökei és együtthatói közötti ismert összefüggés szerint x2 és -x4 az
x2-x-1=0
egyenlet gyökei:
x2=12+121+4,x4=-12+121+4.

A szorzótábla szerint továbbá:
x12-x22=x2-x4=1,
és így
x1=1+x22.

Adott körbe írt szabályos ötszög szerkesztése ennélfogva a következő:
 
 
5. ábra
 

Legyen O az adott kör középpontja és A0 a kör kerületének egy pontja (5. ábra). Az A0 pontban merőlegest állítunk OA0-ra és rámérjük a hosszegységnek választott OA0 körsugár felét. Az így kapott pontot O-val összekötő egyenesdarabból levágjuk a hosszegység felét; ezzel megkaptuk x4-et, amelyet rámérünk az OA0 egyenesre O-tól A0 felé. A hosszegységből és annak feléből szerkesztett derékszögű háromszög átfogóját a hosszegység felével meghosszabbítva megkapjuk x2-t, melyet rámérünk az O pontban OA0-ra emelt merőlegesre. Az így kapott pontot A0-val összekötő egyenesdarab x1-gyel egyenlő. Ha ennek felét az O-tól 12x4 távolságban OA0-ra merőlegesen húzott egyenesre OA0-tól számítva mindkét irányban rávisszük, akkor a keresett ötszög A1 és A4 csúcsát kapjuk, hiszen az OA1A4 szög koszinusza 12x1, tehát a 3. ábra szerint OA1A4∢=18∘. Az ötszög hátralevő két csúcsa, A2 és A3 az A0 pontnak az OA1 és OA4 egyenesekre vonatkozó tükörképe, amelyet meg tudunk szerkeszteni.
Szerkesztésünk annak a felismerésén alapul, hogy adott körbe írt szabályos csillagötszög oldala ugyanazon körbe írt szabályos tízszög oldalából és a kör sugarából mint befogókból szerkesztett derékszögű háromszög átfogójával egyenlő.
*Kürschák József 1902-ben a Mathematische Annalen 55. kötetében megjelent dolgozatában továbbmenve azt is megmutatta, hogy minden szerkesztési feladat, melyet vonalzóval és hosszátvivővel megoldhatunk, akkor is elvégezhető, ha a hosszátvivőt egy alapmérték-kel helyettesítjük, vagyis oly eszközzel, mely csak egy bizonyos, az eszköz által megszabott hosszúságnak (mondjuk a hosszegységnek) az átrakására alkalmas.