Kezdőlap


Cím:	A legnagyobb elem kiválasztása
Szerző(k):	Komjáth Péter
Füzet:	1989/május, 201 - 204. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hány teniszmérkőzésre van szükség, hogy $n$ játékos közül kiválasszuk a legjobbat? Kétkarú mérleg segítségével, $n$ db tárgy közül hány méréssel tudjuk kiválasztani a második legnehezebbet? Ezek a kérdések a számítógép-tudomány egyik legfontosabb fejezetének, a rendezések elméletének alapproblémái. A válaszadáshoz algoritmust, tehát tervet kell készítenünk a mérések végrehajtására, s ha az optimális algoritmust akarjuk megtalálni, arra is képesnek kell lennünk, hogy bebizonyítsuk: nincs jobb.
A programozás elmélete általában a következő modellt alkalmazza. Adva van $n$ adat, $A_{1}$ , $...$ , $A_{n}$ , amelyek valamilyen sorrendben rendezve vannak. Ez a sorrend számunkra ismeretlen, de akármikor összehasonlíthatunk bármely két adatot, ezáltal megkapva egymáshoz viszonyított elhelyezkedésüket. Cél a legnagyobb, második legnagyobb stb. elem meghatározása, a lehető legkevesebb összehasonlítással. Logikus lenne feltenni, hogy adataink valós, vagy akár természetes számok, például sportbeli megfogalmazásokban pontszámok. Ezt általában mégsem teszik fel, ugyanis az összehasonlításokból csak a sorrendre következtethetünk, a számok értékére nem. (Szigorúan véve, csak annyit tudunk, hogy adataink között van egy ismeretlen reláció, ami rendelkezik a "kisebb'' reláció szokásos tulajdonságaival, vagyis tranzitív és trichotóm.) A következő leírásokban időnként használni fogjuk a sportélet természetesen adódó kifejezéseit.

1. tétel.

n

adat közül

n - 1

összehasonlítással ki lehet választani a legnagyobbat.

2. tétel.

n

adat közül a legnagyobb kiválasztásához mindig legalább

n - 1

összehasonlításra van szükség.

Az 1. tétel bizonyítása. Két módszert is megadunk. Az elsőben (1. ábra), először

A_{1}

-et és

A_{2}

-t hasonlítjuk össze, majd a "nyertes''-t

A_{3}

-mal, és így tovább. Ez az úgynevezett "kihívásos'' módszer, amikor az egymás utáni mérkőzések során mindig a nyertes marad a (pingpong, sakk stb.) asztalnál.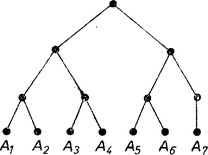

1. ábra

2. ábra

A másik módszer fordulók rendezése (2. ábra). A játszmaszám itt is

n - 1

, hiszen (ugyanúgy, mint az előbb) bármelyik résztvevő egyetlen vesztes játszma után kiesik, és a legjobbat kivéve mindenki kiesik. (A játszmák számának közvetlen, szintenkénti összeszámolása kissé nehezebb: Jelöljük

f (x)

-szel a szükséges játszmaszámot. Nyilván

f (1) = 0

. Ha

x > 1

természetes szám, és

2 ≦ x ≦ 2 y + 1

, akkor a legalsó szinten

y

játszma van, a fölötte levő szinteken pedig

x - y

játékos játszik kieséses játékokat. Tehát

f (x) = y + f (x - y)

, és ebből indukcióval könnyen igazolhatjuk

f (x) = x - 1

-et.)

A 2. tétel bizonyítása. Az eddig elmondottak után ez már igen egyszerű: a nyertesen kívüli

n - 1

játékos mindegyikének vesztenie kell valamikor (különben nem tudhatnánk biztosan, hogy nem ő a legjobb), s minden mérkőzésnek egy vesztese van.
A továbbiakhoz jelöljük

r

-rel azt a természetes számot, amire

2^{r - 1} < n ≦ 2^{r}

teljesül. Ekkor a 2. ábra

r

-fordulós rendszert ad, amiben a győztes éppen

r

-szer játszik.

3. tétel.

n

adat közül a második legnagyobb

n + r - 2

összehasonlítással megtalálható.

Bizonyítás. A 2. ábra szerinti módszerrel

n - 1

összehasonlítással megtaláljuk a legnagyobb elemet. Minden ettől különböző elem "kikapott'' valamelyiktől. A második legnagyobb csak a legnagyobbtól kaphatott ki, ő tehát a legnagyobb által közvetlenül legyőzött

r

elem valamelyike. Ezek közül kell tehát a legnagyobbat megtalálnunk, amit az 1. tétel bármelyik módszerével

r - 1

összehasonlítással megtehetünk. Ez összesen

n - 1 + r - 1 = n + r - 2

összehasonlítás.

4. tétel. Nincs olyan algoritmus, amely minden esetben

n + r - 2

-nél kevesebb összehasonlítással megtalálná a második legnagyobb elemet.

Bizonyítás. Itt már nem igaz, mint a 2. tételben, hogy minden esetben legalább ennyi összehasonlítás kellene. Ha szerencsénk van, az 1. ábra módszerével

n - 1

összehasonlítás is elég lehet (ha mindig erősebb és erősebb új játékos jön).
Tételezzük fel, hogy valamilyen eljárással, bizonyos számú összehasonlítás után meghatároztuk az

M

-mel jelölt második legnagyobb elemet. Biztosan tudjuk tehát, hogy

M

nem a legnagyobb, tehát valamelyik összehasonlításban "veszített''. De csak a (mondjuk

L

-lel jelölt) legnagyobb elemmel szemben veszíthetett, így

L

és

M

mindenképpen összehasonlításra került. Így valahogyan meggyőztük magunkat, hogy

M

a második legnagyobb, és

L > M

-et is tudjuk, tehát mindenképpen tudjuk, hogy

L

a legnagyobb. Kaptuk tehát, hogy a második legnagyobb elem meghatározásához meg kell találnunk a legnagyobb elemet is, így a 2. tétel szerint mindenképpen legalább

n - 1

összehasonlítást tennünk kellett.
Jelölje

p

azon összehasonlítások számát, amelyekben

L

részt vett. Így van

p

elem, ami

L

-től kikapott, közöttük van

M

. Az

M

-től különböző

p - 1

elemről biztosan tudjuk, hogy nem a második legjobbak. Ez csak úgy lehet, hogy ezek még valami mástól is kikaptak. Összesen tehát van

(n - 1) - (p - 1) = n - p

olyan elem, ami legalább egyszer, és

p - 1

további elem, ami legalább kétszer kikapott; így a vesztesek, tehát a játszmák száma legalább

(n - p) + 2 (p - 1) = n + p - 2

. Ha valahogy garantálni tudnánk

p ≧ r

-et, készen lennénk.
Belátjuk, hogy minden algoritmusnak van olyan lehetséges kimenetele, amiben

p ≧ r

és ezzel a bizonyítás kész. Egy algoritmus minden lépése egy

A_{i} - A_{j}

összehasonlítás, és hogy mi az

i

és a

j

, az az előző lépésektől függhet. Hogy a fentiek szerinti kívánatos kimenetelt meghatározhassuk, meg kell adnunk az összehasonlítások eredményeit. Mivel azt akarjuk, hogy a leendő nyertes lehetőleg minél több összehasonlításban vegyen részt, célszerű két játékos közül azt nyertesnek nyilvánítani, aki addig többször játszott.
A szabály tehát ez: ha

A_{i}

és

A_{j}

is veretlen, győzzön az, aki eddig többször játszott; ha egyforma sokat játszottak, győzzön bármelyik. Ha

A_{i}

veretlen, de

A_{j}

már kikapott, nevezzük ki

A_{i}

-t győztesnek, ha pedig már mindkét résztvevőnek van veresége, mindegy, hogy kit kiáltunk ki győztesnek. Önkényes kijelöléseinkkel bajba kerülhetünk, ha olyan

A_{i} - A_{j}

párost kell összehasonlítani, amelyről az előző játszmák alapján tudjuk például, hogy

A_{i} > A_{j}

. Algoritmusunkról azonban feltehetjük, hogy ilyen (új információt nem adó) lépéseket nem tesz.
Be kell még látnunk, hogy e választások garantálják

p \geq r

-et. Tegyük fel, hogy a mérkőzéssorozat elkezdése előtt minden játékos felírja egy cédulára a nevét, és első veresége alkalmából átadja a nála összegyűlt cédulákat legyőzőjének. így a torna alatt a cédulák ide-oda vándorolnak, minden pillanatban, valamilyen eloszlásban, a pillanatnyi veretlenek kezeiben vannak. A végén, minden cédula a győztes,

L

kezében lesz.
Igazoljuk, hogy a torna folyamán mindig igaz lesz a következő állítás:
Ha az

A_{i}

veretlen játékos eddig

x

-szer játszott, akkor nála legfeljebb

2^{x}

cédula van. Ezt

x

-re vonatkozó indukcióval látjuk be;

x = 0

-ra igaz, hiszen csak a saját cédulája lehet nála. Ha

A_{i}

A_{j}

-vel játszik, a nála levő cédula-kollekciót csak úgy bővítheti, ha legyőzi az

A_{j}

addig veretlen játékost. Ha

A_{j}

addig

y

-szor játszott, akkor

x ≧ y

-nak kell teljesülnie előírásaink szerint. Így

A_{j}

(az indukció miatt) legfeljebb

2^{y}

cédulát adhat át, így

A_{i}

, aki

x + 1

-szer játszott, most legfeljebb

2^{x} + 2^{y} ≦ 2^{x} + 2^{x} = 2^{x + 1}

cédulát birtokolhat. Állításunkat így indukcióval bizonyítottuk. A torna végén minden cédula a győztes,

L

kezében lesz, így fenti állításunk szerint

2^{p} ≧ n > 2^{r - 1}

, azaz

p ≧ r

adódik, s ezt akartuk belátni.
Még egy olyan érdekes eset van, amikor az optimális összehasonlítás-számot ismerjük. Legyen

x

az a természetes szám, amire

2 x + 1 ≦ n ≦ 2 x + 2

teljesül.

5. tétel.

n

adat közül

n + x - 1

összehasonlítással meghatározhatjuk a legnagyobbat és a legkisebbet is.

Bizonyítás. A 2. ábra módszerével

n - 1

összehasonlítás elég a legnagyobb meghatározására. A legkisebb adat nem lehet az 1. forduló nyertesei között, így a többi

x + 1

elem valamelyike. Közülük az 1. tétel módszerével

x

méréssel megkaphatjuk a legkisebb elemet.

6. tétel. Nincs olyan algoritmus, amely minden esetben

n + x - 1

-nél kevesebb összehasonlítással határozná meg egyidejűleg a legkisebb és a legnagyobb elemet.

Bizonyítás. A 4. tétel bizonyításához hasonlóan azt látjuk be, hogy bármelyik algoritmusnak tudjuk olyan megtörténését konstruálni, ami legalább

n + x - 1

összehasonlítást használ.
Az algoritmus, illetve a mérkőzéssorozat minden fázisához rendeljük hozzá az

\frac{1}{2} a + \frac{3}{2} b

pontszámot, ahol

a

jelöli az adott pillanatban azon játékosok számát, akik már veszítettek, de még nem nyertek játékot, vagy fordítva: nyertek, de még nem vesztettek,

b

pedig azok számát jelöli, akik veszítettek is, nyertek is.
Kezdetben ez a pontszám nyilván

0

. A játéksorozat végén tudjuk, ki a legjobb, ez csak úgy lehet, ha egy játékos kivételével mindegyik vesztett valamikor. Tudjuk ki a legrosszabb, azaz egy (másik) kivételével mindegyik nyert valamikor. Innen adódik, hogy a pontszám

\frac{1}{2} \cdot 2 + \frac{3}{2} \cdot (n - 2) = \frac{3}{2} n - 2

. Ha el tudjuk érni, hogy minden játszmánál legfeljebb eggyel nőjön ez a pontszám, akkor a játszmák száma legalább

\frac{3}{2} n - 2

lesz.

n = 2 x + 2

-re ez

3 y + 1 = n + x - 1

n = 2 x + 1

-re pedig

\frac{3}{2} n - 2 = 3 x - \frac{1}{2}

, azaz a játékok száma legalább

3 x = n + x - 1

.
A kívánt feltétel teljesíthetősége esetszétválasztással könnyen ellenőrizhető. Az érdekes esetek azok, amikor két veretlen, két nyeretlen, illetve két olyan játékos találkozik, akik még nem játszottak. Ilyenkor a pontszám eggyel nő.
Befejezésül szeretném felhívni az érdeklődő olvasók figyelmét Gács Péter és Lovász László Algoritmusok című könyvecskéjére (Műszaki Kiadó, 1978, második kiadás: Tankönyvkiadó, 1987), amely számos, a fentiekhez hasonló problémát, megoldási módszert ismertet, igen olvasmányosan. Cikkünk témakörének igen alapos elméleti, történeti elemzését adja, számos általánosítást, kiterjesztést is ismertet D. E. Knuth: A számítógép-programozás művészete 3. Keresés és rendezés című monográfiája (Műszaki Kiadó, 1988), a 226‐238. oldal között.

Megjegyzések. 1. A 3. és 4. tétel állítása szerepel Bartha G. és mások: Matematikai feladatok gyűjteménye I. Tankönyvkiadó 1988. feladatgyűjteményben, a 317/b feladatban, 410. oldal. Mivel a feladat megoldása nem nyilvánvaló, úgy éreztük a bizonyítást részletezni kell. E célból jelent meg ez a cikk.
2. Az 5. tétel

n

-ről

(n + 2)

-re történő indukcióval is bizonyítható.