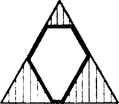Cím: Euréka! Megtalálták! (Megoldások az 1988. decemberi számban kitűzött megoldatlan problémára
Szerző(k):  Keleti Tamás ,  Rechenbach Pál ,  Zsigmond László 
Füzet: 1989/április, 153 - 155. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

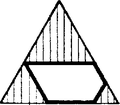
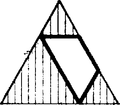
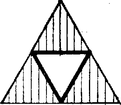
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1988 decemberi számunkban ismertettük a következő problémát, melyet a kanadai Euréka cimű folyóirat egyik régi számában közöltek :

 

(1) Bizonyítsuk be, hogy ha egy szabályos háromszöget 5 egyenlő szárú háromszögre osztunk fel, akkor a részek között csak 0,1 vagy 2 szabályos háromszög fordulhat elő.
 

A bizonyítandó állítás egyik részeként megmutattuk, hogy egy ilyen felosztásban mind az 5 háromszög nem lehet szabályos. Ily módon azt a feladatot tűztük ki, hogy ezekben a felosztásokban 3 vagy 4 szabályos háromszög sem szerepelhet.
Szerkesztőségünk legnagyobb örömére, a feltett kérdésre igen hamar választ kaptunk olvasóinktól, ennek birtokában közölhetjük, hogy a bizonyításra ajánlott sejtés igaz, (vagyis 2-nél több szabályos háromszög valóban nem fordulhat elő.)
Jelenleg 5 dolgozat beérkezéséről számolhatunk be. Lényegében valamennyien azonos módszerrel nyúltak a problémához, teljes megoldást adott Keleti Tamás, Rechenbach Pál és Zsigmond László, kissé hiányos Harcos Gergely és ifj. Kováts Péter dolgozata. Keleti Tamás és Rechenbach Pál foglalkozott a feladat általánosításával is, ezekre egy későbbi számunkban még valamilyen formában visszatérünk.
Megoldóinknak szívből gratulálunk, és további sikeres munkát kívánunk.
Az itt következő megoldás az ő dolgozataik alapján készült.
 

Az (1) állítás bizonyítása.
 

Azt kell belátnunk, hogy egy szabályos háromszöget öt egyenlő szárű háromszögre felosztva, ezek között nem lehet három (vagy annál több) szabályos háromszög. Ezt úgy is fogalmazhatjuk, hogy lennie kell legalább három olyan háromszögnek, amelyik nem szabályos.
 

*
 

A lehetséges felosztás-típusok áttekintése során több alkalommal is felhasználunk további hivatkozás nélkül néhány egészen egyszerű észrevételt. Ilyen megjegyzések a következők:
 

1) Egy egyenlő szárú háromszög pontosan akkor szabályos, ha valamelyik szöge 60 fokos.
 

2) Öt-, vagy ennél nagyobb oldalszámú sokszöget nem lehet két háromszögre bontani. Négyszöget csak valamelyik átlója bonthatja két háromszögre.
3) Konvex ötszög csak valamelyik csúcsából kiinduló két átlójával osztható fel három háromszögre.
Nevezzük az eredeti háromszög egy csúcsát (ill. a hozzátartozó szögét) osztottnak, ha a háromszög felbontása során ez a csúcs egynél több kis háromszögnek is csúcsa.
4) Osztott csúcsnál pontosan annyi kis háromszög keletkezik, ahány részre a megfelelő szöget osztottuk, és ezen háromszögek egyike sem szabályos.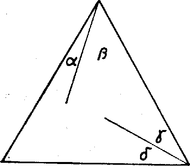
 
 
1. ábra
 

Utóbbi észrevételünk szerint elegendő a szabályos háromszög olyan felosztásait vizsgálnunk, amelyeknél a felosztott csúcsok száma legfeljebb 2, és ezek szögei is csupán két részre vannak felosztva. Tegyük fel, hogy a háromszögnek két osztott csúcsa van (1. ábra). Mivel a két osztóvonal nem esik egybe, ezért a felosztáskor keletkezett szögek közül az α,β,δ szögek három különböző kis háromszöghöz tartoznak, és azok nem szabályosak; ebben az esetben tehát a bizonyítandó állítás igaz.
A továbbiakban így csak két esetet kell megkülönböztetnünk aszerint, hogy az osztott csúcsok száma 0 vagy 1. Foglalkozzunk először az utóbbival; legyen C a felosztott csúcs. A háromszög A és B csúcsánál egy-egy szabályos kis háromszög helyezkedik el; ezek elhagyásával ötszöget vagy négyszöget kapunk (2-3. ábra). Ha a megmaradt rész ötszög (2. ábra), akkor az őt három részre osztó egyik átló biztosan C-ből indul, jelöljük CD-vel; a másik átló ekkor csak 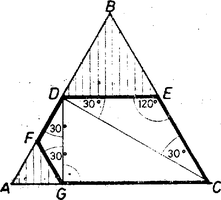DG lehet.
 
 
2. ábra
 

Mivel DFG∢=180∘-60∘=120∘, ezért a DFG egyenlő szárú háromszögben FGD∢=30∘, így DGC∢=180∘-(60∘+30∘)=90∘. Másrészt az ugyancsak 120 fokos szárszögű DEC egyenlő szárú háromszögben ECD∢=30∘, tehát DCG∢=60∘-30∘=30∘. Ez azt mutatja, hogy a DGC (derékszögű) háromszög nem egyenlő szárú, azaz ilyen felbontás nem létezik.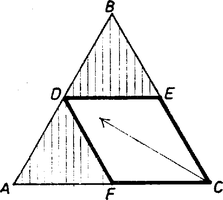
 
 
3. ábra
 

Tegyük fel ezután, hogy az A és B csúcsoknál fekvő (szabályos) kis háromszögek elhagyásával a CEDF négyszöghöz jutunk (3. ábra); CEDF láthatóan paralelogramma, szögei 60 és 120 fokosak. Ha a C-ből kiinduló osztóvonal átmegy a D ponton, akkor az egybevágó CDF és CDE háromszögek egyikét kell még tovább darabolni (az egyik csúcsán átmenő egyenessel) két, egyenlő szárú háromszögre. Ekkor szükségképpen CFD is egyenlő szárú, 120 fokos háromszög; ilyen háromszög azonban nem vágható szét két egyenlő szárú háromszögre. A C-ből kiinduló osztóvonal tehát elkerüli a D pontot, és például a DF szakaszt metszi egy belső H pontjában (4. ábra).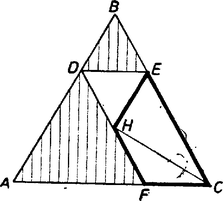
 
 
4. ábra
 

A CEDH négyszöget csak az EH átló vághatja két háromszögre, hiszen C-ből nem indul ki több osztóvonal. Vizsgáljuk meg a keletkezett szögeket! Mivel CFH egyenlő szárú háromszög és CFH∢=120∘, ezért FCH∢=FHC∢=30∘, így HCE∢=30∘. A DHE háromszög szabályos, hiszen a D-nél fekvő szöge 60∘; ezért EHC∢=180∘-(DHE∢+FHC∢)=90∘. Azt kaptuk, hogy a CHE derékszögű háromszög nem egyenlő szárú, tehát ez a felbontás sem elégíti ki problémánk feltételeit.
Nézzük végül azokat a felosztásokat, amelyeknél a háromszögnek nincs osztott csúcsa (5-8. ábra). Ha a három csúcsnál elhelyezkedő szabályos kis háromszögeket elhagyjuk, a visszamaradó sokszög oldalainak száma 6, 5, 4 vagy 3. Az első két esetben a megmaradt síkidom egyáltalán nem vágható szét két háromszögre. A harmadik esetben 60 és 120 fokos szögekkel rendelkező szimmetrikus trapézhoz jutunk; éppen ilyen a 4. ábrán szereplő EHFC trapéz, amelyről beláttuk, hogy nem rakható össze két, egyenlő szárú háromszögből.
 
5. ábra
 
6. ábra
 
7. ábra
 
8. ábra

Végül, ha a visszamaradó alakzat háromszög, akkor az szabályos. Egy ilyen háromszöget két háromszögre vágva, mindkét részben lesz 60 fokos szög, ezért egyik sem lehet egyenlő szárú; így ez a felbontás sem jöhet szóba.