Cím: Egy kétdimenziós rácsgeometriai feladat
Szerző(k):  Hausel Tamás 
Füzet: 1989/március, 104 - 107. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi probléma felvetéséhez az 1988. évi Kürschák József Matematikai Verseny 3. feladata, ill. az arra adott megoldásom vezetett.

 
Legyen e és f két, egymást O-ban metsző egyenes a síkon, és egy-egy (O-tól különböző) pontjuk A és B. Jelöljük meg e minden olyan pontját, amelynek O-tól való távolsága az OA távolság egész számú többszöröse, és hasonlóan jelöljük ki az f egyenes megfelelő tulajdonságú pontjait az OB szakasz szerint. Az e egyenes minden megjelölt pontján keresztül párhuzamost húzunk f-fel, f megjelölt pontjain keresztül pedig e-vel (1. ábra). Az így kapott egyeneseket (beleértve e-t és f-et is) rácsegyeneseknek, a rácsegyenesek metszéspontját pedig rácspontoknak nevezzük. A rácsegyenesek és rácspontok rendszerét röviden paralelogrammarácsnak hívjuk.
 
 
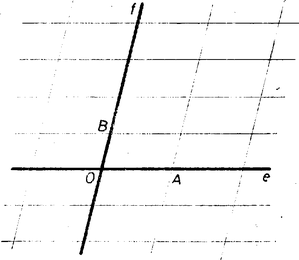1. ábra
 

 
A továbbiakban a rácsok néhány alapvető tulajdonsága közül az alábbiakra lesz szükség:
 
(1) Bármely rács önmagába megy át minden olyan eltolás során, amelyet rácspontól rácspontba mutató vektor határoz meg.
 
(2) Ha A, B, C, D, E, F rácspontok, és az ABC, DEF háromszögek üresek (azaz sem a belsejükben, sem a határukon nincs további rácspont), akkor ABC és DEF területe egyenlő.
 
(Az első állítás igen egyszerűen belátható; a második állítás bizonyítása-megtalálható pl. Hajós Gy., Neukomm Gy., Surányi J.: Matematikai versenytételek II. kötetében, az 1942/2 feladat II‐IV. megoldásában.)
A megoldani kívánt feladathoz két elnevezést vezetünk be. Tegyük fel, hogy van egy paralelogrammarácsunk. Az A, B, C rácspontokat nevezzük összefüggőnek, ha egy egyenesen helyezkednek el, és ott egymást követő rácspontok (azaz semelyik kettő között nincs további rácspont). Az M ponthalmazt tömörnek fogjuk hívni, ha minden pontja rácspont, és a konvex burkához tartozó valamennyi rácspont M-beli.
Ha M tömör halmaz és "elég sok'' pontja van, akkor úgy érezzük, hogy ezek között összefüggő ponthármasnak is lennie kell. Ennél lényegesen több is igaz:

 
(3) Ha M tömör halmaz, és pontjainak száma n, akkor létezik legalább n-4 darab M-beli összefüggő ponthármas.
 
Könnyen látható, hogy (3)-nál erősebb általános becslés nem adható az összefüggő hármasokra. Tetszőleges n (4-nél nagyobb) természetes számra ugyanis legyenek A1,A2,...,An-2 egy r rácsegyenes egymás után következő rácspontjai, és legyen An-1 és An az r-rel párhuzamos, hozzá legközelebb eső egyik rácsegyenes két szomszédos rácspontja. Az M={A1,A2,...,An}, halmaz ekkor nyilván tömör, és a pontjaiból alkotható valamennyi összefüggő ponthármas r-en van ; ezek száma tehát éppen (n-2)-2=n-4 (2. ábra).
 
 
2. ábra
 

Mivel összefüggő ponthármasokat kívánunk találni, szükségünk van olyan feltételre, amiből közvetlenül következtethetünk azok létezésére. E célból először azt vegyük észre, hogy három, egy egyenesbe eső rácspont mindegyike tagja egy-egy olyan összefüggő hármasnak, amelyek valamennyien e három pont konvex burkában helyezkednek el. Ez a konvex burok ugyanis egy szakasz, amelynek bármely három, egymásra következő rácspontja összefüggő.
A (3) állítás igazolásához ezután a következő segédtételt bizonyítjuk be :
 
(4)Tegyük fel, hogy az ABCD konvex négyszög minden csúcsa rácspont, és a négyszög A-nál és B-nél levő szögeinek összege 180∘-nál kisebb. Ekkor a négyszöglemezen van olyan összefüggő hármas, amelynek egyik pontja A vagy B.
 
 
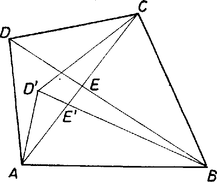3. ábra
 

Legyen E a négyszög átlóinak metszéspontja (3. ábra). Ha az AB¯, AC¯, BD¯ szakaszok valamelyikén van további rácspont is, akkor az állítás igaz. Tegyük fel tehát, hogy AB, AC és BD üresek. Tekintsük az AED háromszöget. Tételezzük fel, hogy ebben található egy további D' rácspont; ekkor az ABCD' négyszög is konvex, továbbá
D'AB∢+ABC∢<DAB∢+ABC∢<180∘.
A kapott négyszög tehát (az eredeti négyszögben van, és) szintén eleget tesz (4) feltételeinek. Jelöljük az átlóinak metszéspontját E'-vel, és az előbbihez hasonlóan vizsgáljuk meg, van-e további rácspont a CE'B háromszögben, stb. Mivel az eredeti négyszöglemez véges számú rácspontot tartalmaz, ezért a fenti lépések ismételgetésével végül eljutunk egy, a (4) feltételeit kielégítő ABC1D1 négyszöghöz, úgy, hogy abban ‐ az átlók metszéspontját E1-gyel jelölve ‐ a C1E1B és D1E1A háromszögek belsejében már nincs rácspont (4. ábra).
 
 
4. ábra
 

A korábbiakhoz hasonlóan most is elegendő azzal az esettel foglalkoznunk, amikor az AC1¯, AD1¯, BC1¯, BD1¯ szakaszok üresek. A C1E1B, D1E1A háromszögek ekkor eleget tesznek (2) feltételeinek, így a területük megegyezik.* Ebből következik, hogy az ABD1 és az ABC1 háromszögek területe is egyenlő, vagyis D1C1 párhuzamos AB-vel. Mivel az A és B csúcsnál levő szögek öszszege 180∘-nál kisebb, ezért D1C1¯<AB¯. A B pontot a C1D1¯ vektorral eltolva tehát az AB szakasz belső pontjához jutunk. Ez a pont azonban (1) szerint maga is rácspont, így A is és B is benne van egy összefüggő hármasban.
Ezután rátérünk (3) bizonyítására. A bizonyítást n szerinti teljes indukcióval végezzük; az állítás nyilvánvalóan igaz, ha n≦4. Tegyük fel, hogy (3) igaz minden olyan esetben, amikor n≦k, és legyen a tömör M halmaz pontjainak száma k+1≧5. Megmutatjuk, hogy M konvex burkának mindig van olyan csúcsa, amely benne van egy (M-beli pontokból álló) összefüggő hármasban. Ha ezt a pontot elhagyjuk M-ből, a maradék k-elemű halmaz tömör lesz, ezért az indukciós feltevés értelmében pontjaiból legalább k-4 darab összefüggő ponthármas választható ki. Ezekhez hozzátéve az elhagyott csúcsot tartalmazó hármast, M-ben legalább (k-4)+1=(k+1)-4 darab összefüggő hármashoz jutunk, és éppen ezt kellett belátni.
A bizonyítás teljessé tételéhez tehát elegendő azt igazolni, hogy a konvex burok valamelyik csúcsa benne van egy összefüggő hármasban. A konvex burok egy sokszög; ha ennek valamelyik oldala a végpontokon kívül tartalmaz még legalább egy rácspontot, akkor ennek az oldalnak bármelyik csúcsa megfelelő. A továbbiakban ezért föltesszük, hogy a konvex burok mindegyik oldala üres.
Ha M konvex burkának öt, vagy annál több oldala van, tekintsük öt egymás után következő csúcsát; legyenek ezek X, Y, Z, T, V. Mivel ZT és TV nem párhuzamosak, ezért az XYZT és az XYTV konvex négyszögek egyike biztosan nem paralelogramma, így alkalmazható rá (4).
Ha a konvex burok négyszög és nem paralelogramma, akkor (4) közvetlenül alkalmazható.
Tegyük fel, hogy M konvex burka az ABCD paralelogramma. Mivel M-nek legalább öt pontja van, és az oldalak üresek, ezért ABCD belsejében található egy Q rácspont. Ha Q rajta van valamelyik átlón , akkor annak az átlónak akármelyik végpontja megfelelő; egyébként ha Q például az ACD háromszög belsejében fekszik, akkor az ABCQ négyszög lesz az, amire felhasználhatjuk a (4) segédtételt. (Az A és B csúcsoknál levő szögek összege itt láthatóan 180∘-nál kisebb ‐ 5. ábra).
 
 
5. ábra
 

 
 
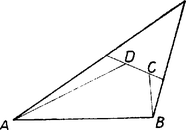6. ábra
 

Utoljára azzal az esettel foglalkozunk, amikor a konvex burok háromszög. Ennek oldalai feltételezésünk szerint üresek, így a háromszög belsejében legalább két pontja van M-nek; legyenek C és D ilyen pontok (6. ábra). Amennyiben a CD egyenes átmegy a háromszög egyik csúcsán, akkor az a csúcs hagyható el az indukciós bizonyításban. Ha nem ez a helyzet, akkor CD például az AB oldalt nem metszi. Az A, B, C, D pontok ilyenkor olyan konvex négyszöget határoznak meg, amelyben az A és B csúcsoknál levő szögek összege 180∘-nál kisebb, hiszen ezek a szögek kisebbek a háromszög megfelelő szögeinél. Ismét alkalmazhatjuk (4)-et, tehát A vagy B elhagyható.
 

 Hausel Tamás (Bp., Fazekas M. Gyak. Gimn., III. o. t.)
 

Helyesbítés: Az indoklás hibás, ugyanis E1 nem feltétlenül rácspont. A két háromszög területe azért egyezik meg, mert a C1D1B és a D1C1A rácsháromszögek belseje is és határa is egyenlő számú rácspontot tartalmaz, ezért e két háromszög ugyanannyi üres rácsháromszögre bontható fel, tehát (2) szerint a területük egyenlő. (H. P. )
*lásd helyesbítés a cikk után