|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Bizonyára sokan ismerik az 1‐25 számokból álló bűvös négyzet gyors felírására alkalmas sziámi szabályt (másképpen kínai vagy indus szabályt), Délkelet-Ázsia matematikusainak még az időszámításunk előtti időkben talált tetszetős eredményét.
Mai szemmel az tartható benne bűvösnek ‐ kifejezőbben: rejtélyesnek ‐, hogy felismerhető számtani művelet végzése nélkül olyanra sikerül az elrendezés, hogy minden sor, oszlop, átló összege ugyanannyi, az összeg 1/5 része, 65. Ez a négyzet bűvös állandója.‐ Meg is adjuk az árát ennek az igazi munka nélkül elért sikernek!
Az elrendezést az 1. ábrán idézem, bár ‐ őszintén szólva, személy szerint ‐ mindig görbe szemmel nézek rá. Ennek a "potya'' receptnek a létezése kisiklatja a probléma helyes értékelését, bénítja a fejlődést. Egészségtelen kultusz is épült rá (ritmus stb.). Miatta passzív a kérdéssel szemben a közfelfogás.
1. ábra
Olyan egyedülvalónak, utánozhatatlannak vélik sokan, mint a Kínai Nagy Fal vagy a Szaturnusz gyűrűje. Pedig félmilliónál is több megoldást lehetne fölírni az -ös problémára néhány nagyobb elv és sok kisebb fogás vegyes alkalmazásával! ‐ Kivétel is és jellemző is az az eset, hogy pár éve valaki a Bolyai Társulattól arról kért tájékoztatást, hogyan kaphatna szabadalmat "találmányára'', egy más, -ös elrendezésre. Csak néhány további példány láttán húzta elő az illető a zsebéből "titkát'', ami azután rendszeres gondolkodásról tett bizonyságot. Rejtélyek nélkül.
Nagyobbítással a sziámi szabály révén minden páratlan rendszámhoz fölírható egy bűvös négyzet az számokból, a páros rendszámokra viszont nincs ilyen egyszerű recept a "nagy bűvös szakácskönyvben''. A párosokhoz újabb elvek alkalmazásával szerkesztettek bűvös négyzeteket. (Természetesen a régi "regulák'' eredményeit is meg lehet magyarázni, miért bűvösek.) Így alakult ki a bűvösnégyzet-problémának egy "nehézség szerinti'' osztályozása: legkönnyebb a páratlanok esete, a párosok közül könnyebbek az alakú rendszámok, végül legnehezebb az alakú ("egyszerűen páros'') rendszámok esete, aminek legkisebb képviselője a 6-os. Bár valami van ebben, mégis elég sekély szempont ez, hiszen mindenki azt tartja könnyűnek, amit már tud ‐ és megfordítva.‐ Egyébként 300 éve múlt már, hogy Frénicle de Bessy francia kutató összeállította a -es megoldások teljes atlaszát, 880 elrendezést, a szimmetrikus állásokat csak egyszer számítva. Pontos létszám csak erre, és az esetre ismeretes; ez utóbbira ez a szám 1 (2. ábra), és ez ‐ a négyzet geometriai szimmetriáinak megfelelően ‐ 8 állásban szemlélhető, tükrözések és forgatások nyomán.
2. ábra
Az alább vázolandó építési elvvel a "nehéz'' -os esetet tesszük könnyűvé. "Modern elem'' benne, hogy mintegy "előgyújtást'' használ fel: úgy készít egy -edrendű bűvös négyzetet, ha valaki megad egy -edrendűt. Egyedül -edrendűt nem tud, mert természetesen senki sem tud beleadni -es megoldást.
Forrásunk szerint az elvet 1918-ban írta le egy levélben R. Strachey. Lényegében aszerint, de mégis némi tágítással és módosítással építünk ki egy -os bűvös négyzetet az 1‐36 számokból, állandója tehát 111 lesz. "Előgyújtásul'' persze a 2. ábrán látható négyzetet használjuk fel, ennek állandója 15.
A mezőt felosztjuk négy, egyenként mezős negyedre, számainkat pedig négy sorozatra, csupa egymás utáni számokból 1‐9-ig, tovább 18-ig, 27-ig, 36-ig. Előkészítésül ezekből írunk be egy-egy bűvös négyzetet, egymástól függetlenül, sorra a bal felső, a jobb alsó, a jobb felső negyedbe, a bal alsóba pedig némi korlátozással (3. ábra). Mintának a 2. ábrát vagy 7 szimmetrikus társának bármelyikét vehetjük, számait az illető sorozat szerint 9-cel, 18-cal, ill. 27-tel növelve. Itt az első három sorozatból beírt bűvös négyzet mintáját tetszőlegesen választottuk a 8 lehetőség közül, a bal alsó negyed mintájául pedig azt vettük, amelyik a fölötte álló negyedbe választott mintának a vízszintes középvonalra való tükörképe. Ezáltal a tábla bal felében a tükrös helyzetű számok különbsége mind a 9 mezőpárban . (Forrásunkban az uralkodó szokás szerint mindhárom előbbi negyed mintája ugyanaz az állás, mi viszont nem akarunk ilyen fétiseket, formabontásunkkal mindjárt a variációs lehetőségekre is fel akarjuk hívni a figyelmet. Ezt értettük az említett tágításon.)
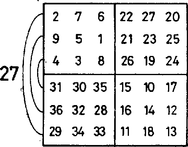 3. ábra
Ez az ábra máris "majdnem bűvös''. Oszlopai bűvösek, sorainak, átlóinak összegei pedig rendszeres eltéréseket mutatnak az állandótól. Ezeket fogjuk megszüntetni rendszeres cserékkel. Az egyes negyedek állandói a 15-höz képest sorra -tel növekednek, a jobb alsóban 42, majd 69, 96. A felső 3 sor összegei hiányt mutatnak, az alsókéi többletet, az átlók pedig 2-szer ekkorát, 54-et, a főátló (a jobbra lejtő) hiányt, a mellékátló többletet. Ezt "a nagybani leltárt'' vázolja a 4. ábra.
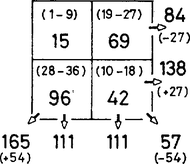 4. ábra
A tábla bal felében végzett 3 szimmetrikus csere útján mindezek az eltérések megszűnnek. Egy-egy cserét végzünk az 1. és 6. sorok között, valamint a további 2 szimmetrikus sorpár között, de úgy, hogy két csere átlóbeli számokkal, a harmadik pedig átlón kívüliekkel történjék. Az 5. ábrán csak a cserélt számok láthatók. Az oszlopösszegek nem változtak, tehát a további 30 mező számait az előbbiből átmásolva kész is a bűvös négyzet.
 5. ábra
Természetesen a következő kérdés az, hogy hány kitöltéshez juthatunk ezzel a módszerrel. A példát, önmagát is beleértve, -féleképpen lehet utánozni. A 8-as tényezők az első három negyed számára a 2. ábra állásának megválasztásaiból származnak, a pedig az 5. ábra mintájára szóba jövő "cserélési térképek'' száma: -féleképpen választható az átlókból cserélő két számpár (ti. annak egyik tagja), és 2-féleképpen a még nem korrigált sorpárból az átlóba nem tartozó szám (ami az 5. ábrán a 36‐9 pár). Mindezek az elrendezések lényegesen különbözők, a négyzet semmiféle szimmetriája nem viszi őket egymásba. ‐ Az eddigi teljesítményt később még majd növekedni látjuk.
Itt említjük meg, hogy az eredetiben csak 2-féle cserélő térképről lehetett szó. Ugyanis Strachey mindegyik negyedbe ugyanazt az állását ajánlotta a 2. ábrának, ezért nála a 27-es különbözetű számpárok nem tengely-tükrösen állnak, hanem három mezővel függőlegesen eltolódva. Emiatt a negyedátlókat külön-külön kellett javítani két-két számpárral. Mindig cserélni kellett a negyedek középszámait, amelyek mindkét átlóba beletartoznak. A két térképet a 6. ábrán vázoltuk. ‐ Ezeket értettük az elv föntebb említett módosításán, vagyis, hogy eltolás helyett tükrözéssel alakítottuk ki a csereképes számpárokat a több variáció érdekében.
 6. ábra
Forrásunk csak a páratlan rendszámok megduplázására ajánlja Strachey eljárását. Bizonyára nem tartották érdekesnek kimondani, hogy az elv a párosokra is használható. (Valóban, csak annak érdemes ezekkel is foglalkoznia, aki ‐ mint egy bélyeggyűjtő ‐ a különböző elvek alapján készült bűvös négyzeteket külön is gyűjti. Másrészt a föntebbi "osztályozás'' szerint azok úgyis könnyebbnek minősültek.) ‐ A nagyobb rendszámok megduplázásakor az előkészítés jobb oldali negyedei is szerephez jutnak, sőt, szükség is van rájuk, mert ott 3-szor kisebb a cserélő számok különbsége. Például esetében a sorpárok eltérése az állandótól le- és fölfelé , az átlóké 250, és egy bal oldali csere -tel tud javítani, aminek sem a 125, sem a 250 nem többszöröse. Besegít viszont a jobb oldali cserék "aprópénznek'' számító 25-ös különbsége. Ilyenkor persze már az is szükséges, hogy jobbról is egyezzék a két negyed mintája, illetve könnyebb, ha azok egymás tükörképei, a bal oldali negyedek közös mintájától viszont ilyenkor is függetlenek.
Mármost a -es rendszám duplázásakor sorpáronként a bal féltáblán , a jobb oldalin számpár cserél úgy, hogy balról , jobbról sor egy cserélője tartozzék bele az átlóba. A -rendű négyzetek megduplázása valóban jóval egyszerűbb: sorpáronként mindkét oldalon számpár cseréljen, és az átlókba is mindkét oldalon pár tartozzék bele. Vagyis itt az előkészített számoknak éppen a fele cserél helyet (a páratlan esetben majdnem a fele). Megjegyzendő, hogy az "aprópénz'' a sorpárokban ellene dolgozik a bal oldali cseréknek, az átlókban viszont egy irányban hatnak az eltérések megszüntetésében. (-tól kezdve csökkenteni lehet a végzendő cserék számát lásd 9. ábra).
Minderről az általános esetben is könnyen meggyőződhetünk. A 4. ábra mintájára ugyanis -nak legfeljebb 3-adfokú polinomjait kapjuk azokban a kifejezésekben, amelyek a negyedek és a nagy négyzet állandóira, továbbá a deficit‐többletekre, ill. az egy cserével elérhető javításokra adódnak. Aki mindezt átgondolja vagy végigszámolja, nagyobb élményt szerez magának, mintha sziámi módon végigszlalomoz akár egy -es négyzetet! És azt is tudni fogja, miért bűvösek új négyzetének a vonalai!
"Modern technikával'' további bűvös négyzeteket nyerhetünk a fönti eljárásból, ha megpróbálunk válaszolni a következő kérdésre: "mit lehetne még mellőzni az előkészítés sok szabályszerűségéből?'' A gazdaságosság elvét mindjárt az ezt vizsgáló ábrába is belevisszük. Következő -os négyzetünket a 0‐35 számkészletből építjük, így a bűvös állandó 105 lesz, a mintákban pedig az 1-esekkel csökkentett 0‐8 számokból 12.
Beírandó számainkat két-két tagra bontjuk, egyik a -as mintából származó "kisebb rész'', a másik a 9-es, 18-as, 27-es növelésekből a "nagyobb rész'', ami az előkészítésben negyedenként még ugyanaz. Ezután a részeket "szétírjuk'' egy-egy külön négyzetbe, az eredeti négyzet komponenseibe (összetevőibe). 7. ábránkon a nagy részek komponensében az óriási 9-es, 18-as azt jelzi, hogy közös mind a kilenc számra. A nagy komponensben már végrehajtottunk 3 cserét valamelyik térkép szerint. Mondhatjuk, hogy a kicsiben is, hiszen ez a felbontás azt mutatja, hogy a kisebb részek komponense "észre sem veszi'' a cseréket, pl. az 1. és a 6. sor 6-osainak a cseréjét a 2. oszlopban ‐ éppen így választottuk meg ugyanis a mintákat.
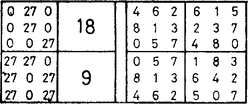 7. ábra
És most bevalljuk: a kis komponens három negyedéből kiloptuk annak a (3-tagú) kis átlónak a bűvösségét, amelyik úgysem tartozik bele a nagy négyzet átlójába: balról fönt és lent egyformán 0+1+2 nem 12, jobbról fönt 6+3+0 sem az, dehát a 3. ábrában sem érvényesült az, hogy 22+23+24 annyi, mint pl. 22+27+20. A jobb alsó negyedben hagytuk meg hírmondónak a 3+4+5=12-es mellékátlót csak azért, hogy lássuk, a kiirtás sem kötelező.
Egybeírva a két komponenst, azaz összeadogatva a részeket, "visszakapjuk'' azt, ami igazában még nem is volt együtt. A felső sor ez lesz: .
Itt is összeszámlálhatjuk a módszerünkkel nyerhető különböző kitöltéseket, de ezt már az érdeklődő Olvasóra hagyjuk.
A kis komponens tulajdonképpen olyan bűvös négyzet, amelyben a 0‐8 számok 4-szer fordulnak elő, és bűvösnek megkívánt vonalain az összeg 24. A nagy komponensről hasonlót mondhatunk, 81-es összegekkel. Lényegében a 9-alapú számrendszerbe átírt alakjukból építettük föl számaink bűvös elrendezését. ‐ Hasonlóan az 5-ös számrendszerbeli alakok használatával lehet "szépen'' belátni az 1. ábra bűvösségét is, ha előzőleg minden számát 1-gyel csökkentjük.
Annyira XX. századi ez az elv, hogy továbbfejlesztve még önmaga sikereit is képes "megrongálni''. Egy másik szép elvvel kombinálva ugyanis kiderül, hogy még gyengébb előkészítésből is adhat bűvös négyzetet. Ezt azonban itt nem ismertetjük.
 8. ábra
9. ábra
Befejezésül a 8‐9. ábrát ajánljuk a kutatásra hajlamos Olvasónak, ezek is a Strachey-elv távoli származékai; a 9. ábra egy 12-edrendű bűvös négyzetnek a felső fele. Reméljük, hogy egy Olvasónk sem értelmezi a fentieket a "ponyvairodalom'' nyelvén, hogy bűvös négyzetet " így kell'' csinálni, hanem helyesen, hogy így is lehet. És persze másképpen is.
Rouse Ball ‐ Coxeter : Mathematical Recreations (11. kiadás, 1963, London, Macmillan). |
 PDF | MathML
PDF | MathML