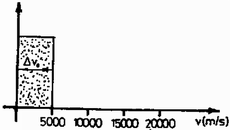Kezdőlap


Cím:	Az 1988. évi (19.) Nemzetközi Fizikai Diákolimpia elméleti feladatainak megoldása
Szerző(k):	Gnädig Péter
Füzet:	1988/november, 397 - 405. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Részecskék sebességének spektroszkópiai vizsgálata Doppler-eltolódás segítségével.
Bevezetés: Az atomok fotonkibocsátása, illetve fotonelnyelése megfordítható folyamat. Erre példa a gerjesztés, majd az azt követő visszatérés az alapállapotba. Így lehetőség nyílik arra, hogy a fotonok elnyelődését a későbbi spontán fotonkibocsátás észlelése révén vizsgáljuk (fluoreszcencia). Modern vizsgálatokban ezt a jelenséget használják fel az atomi részecskék észlelésére és azonosítására, továbbá az atomi részecskenyalábok sebességeloszlásának meghatározására.
Az 1. ábrán látható idealizált kísérleti elrendezésben egyszeresen töltött ionok $v$ sebességgel mozognak egy lézersugárral szemben. A lézer $λ$ hullámhossza változtatható. A nyugalomban levő részecskék $(v = 0)$ $λ_{1} = 600 nm$ hullámhosszal gerjeszthetők. A mozgó részecskék gerjesztéséhez ettől eltérő hullámhossz szükséges a Doppler-effektusnak megfelelően.

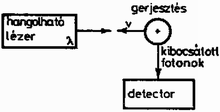1. ábra

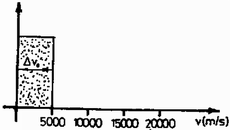2. ábra

Az ionok sebességeloszlása egyenletes

v_{1} = 0

és

v_{2} = 6000 m/s

értékek között. (A 2. ábra a részecskeszámot ábrázolja a részecskesebesség függvényében.) Oldjuk meg a következő

3

részfeladatot:

1.1. A. feladat: Milyen hullámhossz-határok között kell a lézert megváltoztatni ahhoz, hogy minden ion gerjesztődjön? Vázoljuk föl az újrakibocsátott fotonok számának eloszlását a lézer hullámhosszának függvényében!

Megjegyzés: Ebben a részfeladatban a klasszikus Doppler-eltolódás képletével számoljunk!

1.1. B. feladat: Az előző feladat pontos tárgyalásához a Doppler-eltolódás relativisztikus kifejezése szükséges:

\begin{matrix} ν' = ν \sqrt[]{\frac{1 + v / c}{1 - v / c}} . \end{matrix}

Adjuk meg, hogy a klasszikus formula használata milyen nagyságrendű hibához vezet!

1.2. feladat: Tegyük fel, hogy az ionok gerjesztésük előtt

U

nagyságú gyorsító elektrosztatikus potenciálkülönbségen haladnak keresztül. Mi a matematikai kapcsolat a sebességeloszlás szélessége és a gyorsítófeszültség nagysága között? Kiszélesíti vagy elkeskenyíti a feszültség a sebességeloszlást?

1.3. feladat: Egy

e / m = 4 \cdot 10^{6} C/kg

fajlagos töltésű ionnak két állapota van, az ezeknek megfelelő hullámhosszak

λ_{1} = 600 nm

{\bar{λ}}_{1} = λ_{1} + 10^{- 3} nm.

Mutassuk meg, hogy az összes ion gerjesztésekor a lézer két hullámhossz-tartománya átfedésben van, ha nem alkalmazunk gyorsítófeszültséget. Megválasztható-e a gyorsítófeszültség értéke oly módon, hogy ne legyen átfedés a tartományok között? Ha igen, számítsuk ki az ehhez szükséges minimális feszültség értékét!

Megoldás. 1.1A: A fény hullámhossza és frekvenciája között fennálló

λ \cdot ν = c

összefüggés, valamint a

ν' = ν (1 \mp \frac{v}{c})

klasszikus Doppler-képlet felhasználásával az álló részecskék gerjesztési frekvenciájára

ν_{1} = c / λ = 3 \cdot 10^{8} \frac{m}{s} / 6 \cdot 10^{- 7} m = 5 \cdot 10^{11} Hz

,
a leggyorsabban mozgó részecskékre pedig

ν' = ν_{2} \cdot (1 + \frac{v_{2}}{c}) = ν_{1} = 5 \cdot 10^{11} Hz

ismeretében

ν_{2} = \frac{ν_{1}}{1 + \frac{v_{2}}{c}} \approx ν_{1} (1 - \frac{v_{2}}{c})

adódik. Ez annyit jelent, hogy akkor tudjuk valamennyi iont gerjeszteni, ha a lézer frekvenciája

\begin{matrix} ν_{1} - ν_{2} = ν_{1} \cdot \frac{v_{2}}{c} = 5 \cdot 10^{11} Hz \cdot \frac{6000}{3 \cdot 10^{8}} = 10^{7} Hz, \end{matrix}

hullámhossza pedig a

\begin{matrix} λ_{2} - λ_{1} = \frac{c}{ν_{2}} - \frac{c}{ν_{1}} = \frac{c (ν_{1} - ν_{2})}{ν_{1} \cdot ν_{2}} \approx \frac{3 \cdot 10^{8} \frac{m}{s} \cdot 10^{7} \frac{1}{s}}{{(5 \cdot 10^{11} \frac{1}{s})}^{2}} = 12 nm \end{matrix}

intervallumban változtatható. Mivel az ionok sebesség szerinti eloszlása egyenletes, az általuk kibocsátott fény intenzitása (a fotonok száma) is konstans függvény lesz a fentebb kiszámított hullámhossz-tartományban (3. ábra).

3. ábra

1.1B: A pontos relativisztikus képlet szerint

\begin{matrix} \frac{ν'}{ν} = \sqrt[]{\frac{1 + v / c}{1 - v / c}} . \end{matrix}

Mivel

ε = v / c = 2 \cdot 10^{- 5} ≪ 1

, alkalmazhatjuk az

{(1 + ε)}^{n} \approx 1 + n \cdot ε

közelítést:

\begin{matrix} \frac{ν'}{ν} = (1 + \frac{v}{c}) \cdot {(1 - \frac{v^{2}}{c^{2}})}^{- \frac{1}{2}} \approx (1 + \frac{v}{c}) (1 + \frac{1}{2} \frac{v^{2}}{c^{2}}) . \end{matrix}

Az eredmény első tényezője éppen a klasszikus Doppler-képletnek felel meg, az elkövetett (relatív) hiba tehát

\frac{1}{2} \cdot \frac{v^{2}}{c^{2}} = 2 \cdot 10^{- 10}

nagyságrendű.

1.2: Egy

e

töltésű,

m

tömegű részecske

v

nagyságú sebessége

U

potenciálkülönbség hatására

\begin{matrix} v' = \sqrt[]{v^{2} + 2 e U / m} \end{matrix}

értékre nő. A kezdeti sebességeloszlás szélső pontjainak megfelelő

v_{1} = 0

, illetve

v_{2} = 5000 m/s

sebességgel mozgó részecskék sebessége a gyorsítás után

\begin{matrix} v_{1}^{'} = \sqrt[]{2 \cdot e \cdot U / m}, illetve \\ v_{2}^{'} = \sqrt[]{v_{2}^{2} + 2 \cdot e \cdot U / m}, \end{matrix}

a sebességeloszlás szélessége tehát

\begin{matrix} v_{2}^{'} - v_{1}^{'} = \sqrt[]{v_{2}^{2} + 2 e U / m} - \sqrt[]{2 \cdot e \cdot U / m} \end{matrix}

értékre változik. Könnyű belátni, hogy ez kisebb, mint

v_{2}

, a sebességeloszlás tehát a gyorsítófeszültség hatására összeszűkül. (Szorozzuk meg a fenti egyenletet a két négyzetgyökös kifejezés összegével, majd fejezzük ki a sebességeloszlás gyorsítás utáni, illetve eredeti szélességének arányát!)

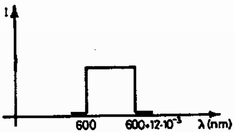
1.3: Ha egy álló iont

λ_{1}

hullámhosszúságú lézerfénnyel lehet gerjeszteni, akkor a különböző sebességgel mozgó ionok halmaza ‐ mint láttuk ‐ a

λ_{1}

és

λ_{2} = λ_{1} + 12 nm

hullámhosszak között hangolható lézerrel gerjeszthető. Hasonlóan a

λ_{1}

(nyugalmi) hullámhossznak is egy bizonyos

(λ_{1}, λ_{2})

intervallum felel meg (4. ábra). A két gerjesztési spektrum akkor fedi át egymást, ha a Doppler-eltolódásból adódó

λ_{2} - λ_{1}

szélesség nagyobb, mint az ion két különböző kvantumállapotának megfelelő

{\bar{λ}}_{1} - λ_{1}

hullámhossz-különbség. A jelen esetben ez valóban fennáll!

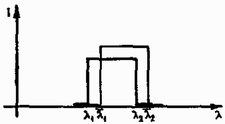4. ábra

Ha az ionokat elektromos erőtérrel gyorsítjuk, sebességük, s a Doppler-effektus miatt az őket gerjeszteni képes lézerfény hullámhossza is megváltozik. Jelöljük ezeket a megváltozott hullámhosszakat

λ^{'}

-vel! A két gerjesztési spektrum átfedése akkor szűnik meg, ha

{\bar{λ}}_{1}' > λ_{2}^{'}

. Mivel

\begin{matrix} \bar{λ}'_{1} = (λ_{1} + 10^{- 3} nm) (1 + \frac{\sqrt[]{2 e U / m}}{c}) \approx λ_{1} + 10^{- 3} nm + λ_{1} \frac{\sqrt[]{2 e U / m}}{c} \end{matrix}

(hiszen

λ_{1} ≫ 10^{- 3} nm

és

\sqrt[]{2 e U / m} ≪ c

), valamint

\begin{matrix} λ'_{2} = λ_{1} (1 + \frac{v'_{2}}{c}) = λ_{1} (1 + \frac{\sqrt[]{v_{2}^{2} + 2 e U / m}}{c}), \end{matrix}

az átfedés megszűntének feltétele

\begin{matrix} \sqrt[]{v_{2}^{2} + 2 e U / m} - \sqrt[]{2 e U / m} < c \cdot 10^{- 3} nm / λ_{1} . \end{matrix}

Bevezetve az

x = 2 e U / m

v_{2}^{2} = a

és

c \cdot 10^{- 3} nm / λ_{1} = b

jelöléseket, a

\begin{matrix} \sqrt[]{a + x} - \sqrt[]{x} < b \end{matrix}

egyenlőtlenséget kapjuk, amelynek megoldása

\begin{matrix} x > \frac{{(b^{2} - a)}^{2}}{4 b^{2}}, \end{matrix}

azaz

U > 150 V

. Ekkora gyorsítófeszültség képes a Doppler-kiszélesedés miatt átfedésbe került spektrumvonalakat szétválasztani.

2. feladat: Maxwell-korong

Bevezetés: Egy

M = 0,40 kg

tömegű,

R = 0,060 m

sugarú,

d = 0,010 m

vastag egyenletes tömegeloszlású hengeres korongot két egyenlő hosszúságú fonálra függesztünk fel. A fonalak egy

r

sugarú, a korong középpontján átmenő tengelyhez csatlakoznak (a fonalak tömege és vastagsága, valamint a tengely tömege elhanyagolható). A fonalakat a tengelyre felcsévélve a korongot (a tömegközéppontját)

H = 1,0 m

magasságba emeljük, majd elengedjük, hogy letekeredjen (5. ábra). A korong pályájának legalsó pontját elérve újra emelkedni kezd. Oldjuk meg a következő feladatokat azzal az egyszerűsítő feltevéssel, hogy az

A

pillanatnyi forgástengely mindig a

P

felfüggesztési pont alatt helyezkedik el, vagyis a fonalak mindig függőlegesek maradnak (6. ábra).

5. ábra

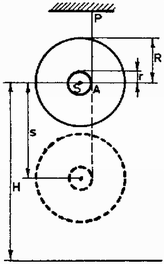6. ábra

Oldjuk meg az alábbi

5

részfeladatot!

2.1. feladat: Mekkora

ω

szögsebességgel rendelkezik a forgó korong az

S

tömegközéppont

s

nagyságú süllyedése után?

2.2. feladat: Mekkora a korong

E_{trans}

haladási (transzlációs) mozgási energiája

s = 0,50 m

süllyedés után? Határozzuk meg számszerűen, hogy ez az energia hogyan aránylik a feladatban szerepet játszó többi energiákhoz ebben a pillanatban, ha a tengely sugara

r = 0,0030 m

2.3. feladat: Határozzuk meg az egyes fonalakban ható

T_{1}

feszítőerőt a korong leereszkedése közben!

2.4. feladat: Számítsuk ki a korong

ω'

szögsebességét a

Φ

elfordulási szög függvényében a 7. ábrán látható átfordulási fázisban! Ábrázoljuk (legalább kvalitatíven) a korong tömegközéppontjának elmozdulás- és sebességösszetevőit (alkalmasan választott Descartes-féle derékszögű koordinátarendszerben) a

Φ

elfordulási szög függvényében!

7. ábra

2.5. feladat: A fonál legfeljebb

T_{m} = 10 N

feszítőerőt bír ki. Mekkora lehet maximálisan a fonalak

s_{m}

lecsavarodási hossza, hogy ne következzék be szakadás az átfordulási fázisban?

Megoldás: 2.1: Az energiamegmaradás tétele szerint

\begin{matrix} M g H = M g (H - s) + \frac{1}{2} Θ ω^{2} + \frac{1}{2} M r^{2} ω^{2}, \end{matrix}

ahol

Θ

a korong tehetetlenségi nyomatéka. Innen

\begin{matrix} ω = \sqrt[]{\frac{2 M g s}{Θ + M r^{2}}} . \end{matrix}

2.2: A test helyzeti energiájának változása az induláshoz képest

\begin{matrix} E_{h} = M g s \approx 2 J . \end{matrix}

A forgási energiája

\begin{matrix} E_{f} = \frac{1}{2} Θ \cdot ω^{2} = \frac{1}{4} M \cdot R^{2} \cdot ω^{2}, \end{matrix}

a haladó mozgás energiája pedig

\begin{matrix} E_{t} = \frac{1}{2} M v^{2} = \frac{1}{2} M \cdot r^{2} \cdot ω^{2}, \end{matrix}

ezek aránya tehát

\begin{matrix} \frac{E_{t}}{E_{f}} = 2 {(\frac{r}{R})}^{2} = \frac{1}{200} . \end{matrix}

Mivel

E_{t} + E_{f} = E_{h}

E_{t} = E_{h} / 201 \approx 10^{- 2} J

és

\frac{E_{f}}{E_{h}} = \frac{200}{201}

2.3: A korong tömegközéppontjának gyorsulását

a

-val, a szöggyorsulást

β

-val, a fonalakban ébredő teljes erőt pedig

T

-vel jelölve a mozgásegyenletek:

\begin{matrix} M g - T = M a, \\ T r = Θ β, \\ a = β \cdot r . \end{matrix}

Innen

Θ = M R^{2} / 2

felhasználásával

\begin{matrix} T = \frac{M g}{1 + 2 {(r / R)}^{2}} . \end{matrix}

Az egyes fonalakat

T / 2 = 1,95 N

erő feszíti.

2.4: Mindenekelőtt meg kell jegyezzük, hogy a feladat szövegében szereplő egyszerűsítő feltevés a korong átfordulása alatt nem teljesülhet. Ha ugyanis a felfüggesztő fonalak mindvégig függőlegesek maradnának, akkor a korongra nem hatna vízszintes irányú erő, s Newton II. törvénye értelmében a tömegközéppontja nem gyorsulhatna vízszintes irányban. Márpedig az egyszerűsítő feltétel szükségszerűen együttjár egy ilyen gyorsulás feltételezésével! A tényleges mozgás során a korong tömegközéppontja majdnem pontosan függőlegesen mozog. Az átfordulás alatt a fonál ,,átcsapódik'' a tengely túlsó oldalára, s mivel a függőlegestől csak nagyon kicsit tér el, számottevő vízszintes erőt nem képes kifejteni. (Sajnálatos módon a diákolimpián a Nemzetközi Zsűri ennek az átcsapódási folyamatnak a részletes végiggondolását túlságosan nehéznek ítélte, és ehelyett a hibás, a Newton-egyenleteknek ellentmondó feltevés alapján történő számítást várta el a versenyzőktől.)
A fonál

P

felfüggesztési pontját választva a koordinátarendszer kezdőpontjának és az

x

-tengelyt vízszintesen, az

y

-tengelyt pedig függőlegesen lefelé irányítva a tömegközéppont koordinátái az átfordulási fázisban:

\begin{matrix} s_{x} = - r cos Φ, \\ s_{y} = H + r sin Φ . \end{matrix}

Az energia-tétel szerint a forgás szögsebessége

\begin{matrix} ω = \sqrt[]{\frac{2 M g (H + r \cdot sin Φ)}{Θ + M r^{2}}}, \end{matrix}

de mivel

H ≫ r sin Φ

és

Θ ≫ M \cdot r^{2}

, az átfordulás alatt a szögsebesség jó közelítéssel

\begin{matrix} ω (Φ) \approx \sqrt[]{\frac{2 M g H}{Θ}} = állandó \end{matrix}

értéknek vehető. Így

Φ = ω \cdot t

, azaz

\begin{matrix} S_{x} = - r cos ω t, \\ S_{y} = H + r sin ω t, \end{matrix}

melyek deriválásából, vagy az egyenletes körmozgás hasonló képleteire való hivatkozással a sebességeket is felírhatjuk:

\begin{matrix} v_{x} = r \cdot ω sin ω t = r \cdot ω \cdot sin Φ, \\ v_{y} = r \cdot ω \cdot cos ω t = r \cdot ω \cdot cos Φ . \end{matrix}

(Ha ismételt deriválással a tömegközéppont gyorsulását is kiszámítanánk, rögtön nyilvánvaló lenne, hogy ellentmondásba kerülünk a dinamika alaptörvényével. A valóságban csak a függőleges elmozdulásra, illetve sebességkomponensre vonatkozó összefüggések fogadhatók el (nagyon jó közelítéssel), az

s_{x}

-re és

v_{x}

-re felírt egyenletek hibásak!)

2.5: Az átfordulás alatt a korong ,,ránt'' egyet a fonálon. Az erőlökés nagyságát durván az impulzusváltozás nagyságából és az átfordulás idejéből becsülhetjük meg:

\begin{matrix} M g - T_{átlag} = \frac{Δ p_{y}}{Δ t} = - \frac{2 \cdot M \cdot r \cdot ω}{π / ω}, \end{matrix}

ahonnan

\begin{matrix} T_{átlag} = M \cdot g + \frac{2}{π} \cdot M r ω^{2} . \end{matrix}

Pontosabb számolással meghatározhatjuk a fonalakat feszítő legnagyobb erőt is. A tömegközéppont gyorsulása a pálya legalsó pontján maximális:

\begin{matrix} a_{max} = r \cdot ω^{2}, \end{matrix}

ahonnan az egyes fonalakat feszítő legnagyobb erő:

\begin{matrix} T_{max} = \frac{1}{2} M g + \frac{1}{2} M \cdot r \cdot ω^{2} . \end{matrix}

Ez akkor nem haladja meg a megengedett

10 N

-os értéket, ha

\begin{matrix} s_{m} ≦ (\frac{2 \cdot T_{max}}{M g} - 1) \cdot \frac{R^{2}}{4 r} = 0,72 m. \end{matrix}

3. feladat: Rekombinációs folyamatok gázkisülésben.

Bevezetés. Elegendően magas hőmérsékletű gázkisülési cső különböző fajtájú ionokat tartalmaz. Vannak közöttük olyan ismeretlen

Z

rendszámú atomok, amelyek egy kivételével valamennyi elektronjukat elvesztették. Ezeket a továbbiakban

A^{(Z - 1) +}

módon jelöljük.

\begin{matrix} ε_{0} = 8,854 \cdot 10^{- 12} As/Vm, \\ e \end{matrix}