Cím: 1988. évi fizika OKTV
Szerző(k):  Vermes Miklós 
Füzet: 1988/október, 321 - 327. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A verseny három kategóriában folyt le. Az I. kategóriában a szakközépiskolai tanulók versenyeztek. A II. kategóriába tartozott minden III. osztályos tanuló (kivéve a speciális és komplex tantervű osztályokat), továbbá azok a IV. osztályos tanulók, akik fizikából semmiféle fakultáción sem vettek részt. A III. kategóriába tartoztak a fizikából fakultáción részt vevő IV. osztályos tanulók, továbbá a speciális és komplex tantervű III. és IV. osztályos tanulók. A II. és III. kategóriában a feladatok ugyanazok voltak. A verseny első fordulója január 4-én, második fordulója március 9-én, harmadik fordulója április 22-én folyt le.

 
EBBEN AZ ÉVBEN VALAMENNYI FELADAT DR. NAGY LÁSZLÓTÓL SZÁRMAZOTT, AKI TAVALY HUNYT EL ÉS AKI ÉVEKEN ÁT SOKAT TETT A TANULMÁNYI VERSENYEK SIKERÉÉRT.
 
Az I. forduló feladatai a II. és III. kategóriában

 
1. Egy 76cm hosszú Torricelli-cső helyzete 30∘- os, félig tölti meg a higany (1. ábra). A hőmérséklet 0∘C. A légköri levegő nyomása 76cm-es higanyoszlop nyomásával egyenlő.
a) Milyen magasan tölti meg a higany a csövet, ha azt függőlegesre állítjuk?
b) Ezután hány fokos hőmérsékleten lesz a higany felső szintje 19cm magasan?
 

Megoldás. A nyomás mértékéül a higanyoszlop magasságát, a térfogat mértékéül a légoszlop hosszát vehetjük. A Boyle-Mariotte-törvény szerint:
(76-19)⋅38=(76-x)⋅(79-x),
innen x=29,46cm.
 
 
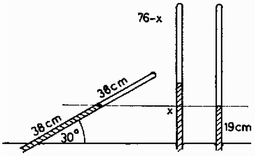1. ábra
 

Az általános gáztörvény szerint:
(76-19)⋅(76-19)T=(76-29,46)⋅(76-29,46)273;
innen T=1,5⋅273K=409,5 K, t=136,5∘C.
 
2. Kondenzátor nagy területű lemezeinek távolsága d=3 cm (2. ábra). A lemezek közötti feszültségkülönbség U=60000 volt. Mekkora v sebességgel kell egy Q=4⋅10-3 coulomb töltésű, m=5⋅10-6 kg tömegű apró testet vízszintesen, d lemeztávolság fele magasságában a homogén térbe belőni, hogy az egyik kondenzátorlemezt h=12 cm távolságban érje el?
 
 
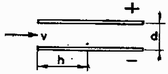2. ábra
 

Megoldás. A térerő E=60000V/0,03  m=2  ⋅106   V/m=2  ⋅106   N/C. Az apró testre ható erő F=QE=8000 newton. Az erővonalak irányában létrejövő gyorsulás a=F/m=1,6⋅109  m/s2. Az erővonalak irányában megteendő távolság 0,015=1,6⋅109⋅t2/2. A mozgás ideje innen t=4,33⋅10-6s. A vízszintesen megteendő távolság 0,12m=v⋅4,33⋅10-6s. A keresett sebesség: v=27714  m/s.
 
3. Az 1 méter hosszú, mindkét végén zárt csőben 0,5 méter hosszú higanyoszlop van (3. ábra). Amikor a cső nyugalomban van, akkor a jobb oldali 0,5 méter hosszú részben 105 Pa nyomású levegő van. A higany sűrűsége 13,6g/cm3.
a) Hol helyezkedik el a higany a csőben, amikor az vízszintes síkban az OO függőleges tengely körül 1,154s-1 fordulatszámmal forog? b) Vizsgáljuk meg az egyensúlyi helyzet stabilitását!
 
 
 
3.a ábra
 

 
 
3.b ábra
 

Megoldás. x jelenti a higanyoszlop eltolódását méterben számítva. Az Am2 alapterületű, 0,5 m hosszú higanyoszlop tömege 0,5⋅A⋅13600kg. Forgáskor a levegő nyomása pPa, a levegő térfogata (0,5-x)Am3. ω=2π⋅1,154=7,247s-1. A higany közepes távolsága a tengelytől (x+0,25) méter. A higanyt a körpályára kényszerítő erő:
F1=0,5⋅A⋅13600⋅ω2⋅(x+0,25).
Az elzárt levegőre alkalmazva Boyle-Mariotte törvényét:
105⋅0,5⋅A=p(0,5-x)A.
Az elzárt levegő nyomóereje:
F2=Ap=0,5⋅105⋅A0,5-x.
Ha x=0, akkor F1=89280⋅A kisebb, mint F2=105⋅A. Következésképpen az x=0 egy egyensúlyi helyzet, amely F1<F2 miatt stabil. Ha x>0, akkor F1=F2 jelent egyensúlyt:
0,5⋅A⋅13600⋅ω2⋅(x+0,25)=0,5⋅105⋅A0,5-x.
Rendezve: 0,5⋅x2-0,125⋅x+0,0075=0. Megoldása: x1=0,15 méter, x2=0,1 méter.
 
 
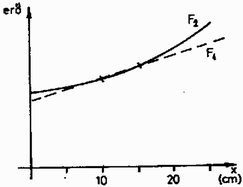4. ábra
 

A körmozgáshoz szükséges erő a távolsággal lineárisan növekszik (4. ábra): 3,57⋅105⋅A⋅x+0,893⋅105⋅A. A levegő nyomóereje hiperbola-függvény szerint változik: 0,5⋅105⋅A0,5-x.
Az egyensúlyi helyzeteket az egyenes és a hiperbola metszéspontjai jelentik. Az x1=0,1 méter labilis egyensúlyi helyzetet jelent, mert ha a higany például kifelé mozdul el, akkor a levegő nyomása kisebb, mint ami a szükséges erő a körmozgás számára, a higany tovább megy kifelé, amíg el nem éri az x2=0,15 méternél a stabilis egyensúlyi helyzetet. Amennyiben a szögsebesség nagyobb, az egyenes emelkedik. ω=7,67s-1 esetében a labilis egyensúlyi helyzet x1=0, a stabilis x2=0,25m. Kisebb szögsebességnél ω=7,231s-1 esete érdekes. Ekkor az egyenes érinti a hiperbolát, egyetlen egyensúlyi helyzet van x=0,125 méternél. Ez az egyensúlyi helyzet kifelé történt elmozdulás esetében stabilis, befelé történő elmozdulás esetében labilis, a higany benyomódik a tengelyig. Még kisebb szögsebesség esetében a higany ott marad a tengelynél. Ezért az x=x2 egyensúlyi helyzet úgy nem jöhet létre, hogy a csövet nyugalmi állapotból kiindulva kezdjük mindig gyorsabban forgatni, ilyenkor a higany az x=0 egyensúlyi helyzetben marad.
 
4. Egy r=1 méter sugarú, m=5kg tömegű abroncs kerületére ugyancsak m=5 kg tömegű nehezéket erősítettünk (5. ábra). Az abroncsot vízszintes síkra helyezzük. A súrlódás elhanyagolható. g=10m/s2. Kezdő helyzetben a nehezék legfelül van. Ekkor az abroncsot elengedjük.
a) Mekkora az abroncs középpontjának a gyorsulása, amikor a nehezék a középponttal egyező magasságban van?
b) Mekkora erővel nyomja ekkor az abroncs a talajt?
 
 
5. ábra
 

 
 
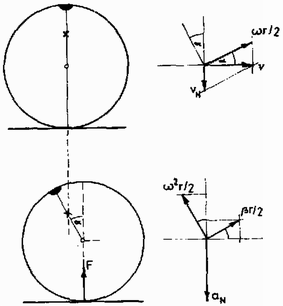6. ábra
 

Megoldás. A súlypont a rádiusz felében van (6. ábra). A súlypont függőleges egyenes mentén mozog lefelé, sebessége vN, gyorsulása aN (mindkettő függőleges irányban). A középpont sebessége v, gyorsulása a (mindkettő vízszintes irányban). A szögsebesség ω, a szöggyorsulás β. A pillanatnyi sebességek α függvényében:
vN=ω⋅r2⋅sinα,v=ω⋅r2⋅cosα.
A súlypont körüli tehetetlenségi nyomaték Θ=1,5⋅m⋅r2. Az energiamegmaradás törvénye szerint:
2mg⋅r2(1-cosα)=2mvN22+12⋅ω2⋅Θ.
Ezekből az egyenletekből megkapjuk a sebességeket mint a szög függvényét:
vN=sinα=gr(1-cosα)4-cos2α,v=cosαgr(1-cosα)4-cos2α,ω=4g(1-cosα)r(4-cos2α).


A forgás törvénye szerint: F⋅r2⋅sinα=βΘ, a súlypont lineáris mozgására nézve: 2maN=2mg-F1, a súlypont függőleges gyorsulása: aN=ω2⋅r2⋅cosα+r2⋅β⋅sinα. Az egyenletrendszer megoldása:
F=2mg⋅3(4-2cosα+cos2α)(4-cos2α)2,
β=Fsinα3mr,aN=g-F2m.
A feladatban szereplő hat mennyiségnek α szögtől való függését mutatja a 7. ábra.
 
 
7. ábra
 

A feladat kérdéseire megkapjuk a választ, ha α helyébe 90∘-ot helyettesítünk:
a=-5m/s2,F=75newton;
továbbá α=90∘-hoz tartozóan ω=10s-1=3,16s-1, β=1,25s-2, v=0, vN=10/2m/s=1,58m/s, aN=2,5m/s2.
Ha csak a feladat numerikus kérdéseire akarunk válaszolni, akkor sokkal hamarabb érünk célt, ha azonnal a 90∘-hoz tartozó értékekkel írjuk fel az egyenleteket.
 
A II. forduló feladatai a II. és III. kategóriában
 

1. Egy rugó nyújtatlan hossza L0=0,6 méter, rugóállandója D=80 N/m (8. ábra). A rugó alsó végét a talajon fekvő m=2 kg tömegű testhez erősítjük, felső végét a test felett tartjuk a rugó nyújtatlan állapotában 0,6 méter magasan. Ezután a rugó felső végét v0=0,5 m/s állandó sebességgel emeljük. g=10 m/s2.
a) Milyen magasan van a test 1,75 másodperc múlva?
b) Mennyi munkát végeztünk ez alatt?
c) A teljesítmény az idő milyen függvénye szerint változik?
 
 
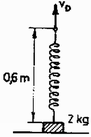8. ábra
 

Megoldás. A test 0,5 s múlva válik el a talajtól, ekkor lesz a rugóerő 20 newton. Most a megnyúlás 0,25 méter. A kéz magassága mint az idő függvénye (9.ábra):
S=0,6+0,5⋅t.

 
 
9. ábra
 

0,5 másodperckor egy rezgés indul meg, szögsebessége ω=D/m=40=6,32s-1, rezgésideje T≈1 s. A rezgés legnagyobb sebessége 0,5=ωr, innen az amplitúdó r=0,5/ω=40/80=1040=0,079 m.
A 0,5 s múlva érvényes függvények:
a test magassága: s=0,5(t-0,5)-1040sin[40(t-0,5)],
a rugó hossza: H=S-s=0,85+1040sin[40(t-0,5)],
a rugó nyúlása: N=H-L0=0,25+1040sin[40(t-0,5)],
a test sebessége: v=0,5-0,5⋅cos[40(t-0,5)].
a) Az s képletébe való behelyettesítéssel, t=1,75 s-kor s=0,546 méter.
b) t=1,75 s-kor a test sebessége v=0,53 m/s, a rugó megnyúlása N=0,329 méter.
Az emelés munkája mgs=10,92 joule. A rugónyújtás munkája DN2/2=4,33 joule. A mozgási energia megszerzéséhez szükséges mv2/2=0,28 joule. A teljes munkavégzés ezek összege: 15,53 joule.
c) A pillanatnyi teljesítmény P=v0F. 0,5 s-ig csak rugónyújtás van, ekkor az erő F=Ds=Dv0t, a teljesítmény P=Dv02t=20t. 0,5 s után az erő F=DN. A teljesítmény: P=10+10sin[40(t-0,5)].
 
2. Adva van egy kettős dugattyúrendszer a 10. ábra szerinti elrendezésben. A falak és a dugattyúk hőszigetelők. Kezdetben a három térrész mindegyikében a levegő nyomása 20 N/cm2, a hőmérséklet 0∘ C. A bal oldali térrészben elhelyezett izzószálat rövid ideig fűtjük, ennek következtében a dugattyúk 5 cm-rel jobbra tolódnak.
a) Mekkorák a kialakult új nyomások?
b) Mennyi hőt adott át az izzószál?

A levegő sűrűsége normál állapotban 1,3dm3, fajhője állandó térfogaton 0,7J/gK, állandó nyomáson 0,98 J/gK.
 
 
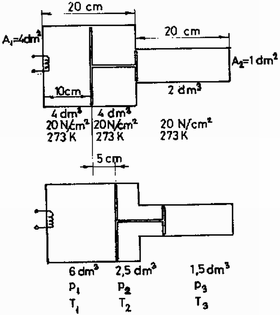10. ábra
 

Megoldás. A fajhőhányados 0,98/0,7=1,4=κ. Az adiabatikus változás törvénye szerint a nyomások a jobb oldali részben:
p3=20⋅(21,5)1,4=29,92N/cm2,
a középső részben
p2=20⋅(42,5)1,4=38,62N/cm2.
A bal oldali rész nyomását a dugattyúrendszer egyensúlyából kell kiszámítani, mert itt a változás nem adiabatikus:
p1⋅4+38,62⋅1=38,62⋅4+29,92⋅1,
innen
p1=36,44N/cm2.

A hőmérsékleteket az általános gáztörvényből számítjuk ki:
T1=273⋅36,44⋅620⋅4=746,11K,    T2=273⋅38,62⋅2,520⋅4=329,48 K,
T3=273⋅29,92⋅1,520⋅2=306,31K.
A gázok tömegei: m1=4⋅2⋅1,3=10,4 gramm, m2=4⋅2⋅1,3=10,4 gramm, m3=2⋅2⋅1,3=5,2 gramm.
A hőfokváltozások: ΔT1=746,11-273=473 K, ΔT2=329,48-273=56,48 K, ΔT3=306,31-273=33,31 K. Az energianövekedések: 0,7⋅10,4⋅473,11=3444,2 joule, 0,7⋅10,4⋅56,48=411,2 joule, 0,7⋅5,2⋅33,31=121,2 joule. Az összes levegő belső energiájának növekedése ezek összege:
ΔE=344,2+411,2+121,2=3976,6joule.
Mivel nincs munkavégzés, ezért ennyi hőt kellett beadni:
ΔQ=3976,6joule.

 
3. A AB=0,02 tesla indukciójú homogén mágneses térben ugyanazon az erővonalon két pont van egymástól XY¯=L=10 cm távolságban (11. ábra). Az X ponton 800 volt feszültséggel felgyorsított elektron halad át, sebessége az erővonalakkal α szöget zár be. Mekkora legyen az α szög, hogy az elektron Y ponton is áthaladjon? Az elektron töltése 1,6⋅10-19 coulomb, tömege 9⋅10-31 kg.
 
 
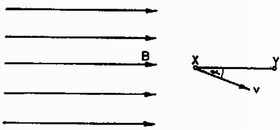11. ábra
 

Megoldás. Az elektron sebessége QU=mv2/2 alapján v=1,686⋅107m/s. A BQvsinα Lorentz-erő biztosítja a körpályán tartáshoz szükséges mv2sin2α/r erőt:
BQvsinα=mv2sin2α/r,
innen a kör sugara:
r=mvsinαBQ.
Az elektron vsinα sebességgel ezt a kört T=2πm/BQ=1,766⋅10-9s alatt futja körül, akármerre indul is.
Az L távolság megtevésének ideje L/vcosα, ez T-nek egész számú többszöröse kell, hogy legyen.
Lvcosα=n⋅2πmBQ,
innen
cosα=1n⋅BQL2πmv=3,358n.
Az α=0 triviális esetet kivéve legalább 4 körülfordulásnak kell végbemennie:
n=4,cosα=0,8395,α=32,91∘,n=5,cosα=0,6716,α=47,81∘stb.  



 
A III. forduló
 
A harmadik (kísérleti) fordulóban a versenyzőknek megfigyelésük alapján meg kellett becsülni azt az áramerősséget, amely a szupravezető anyagmintában folyik, amikor egy kis, 0,05 gramm tömegű mágnest tart lebegve.
 
Az 1988. évi verseny eredménye

 
II. kategória

 
1. díj: Drasny Gábor (Budapest, Fazekas M. G. IV. o. t., tanára: Horváth Gábor)
2. díj: Keleti Tamás (Budapest, Fazekas M. G. IV. o. t., tanára: Horváth Gábor)
3. díj: Andrejkovics István, (Debrecen, Tóth Árpád G. IV. o. t., tanára: Kovács Miklós)
 

A további helyezettek: 4. Bartucz János (Budapest, I. István G. IV. o. t., t.: Cseh Géza). 5. Bordás Ferenc (Szeged, Radnóti M. G. III. o. t., t.: Dudás Zoltánné és Győri István). 6. Asztalos Balázs (Budapest, I. István G. IV. o. t., t.: Cseh Géza). 7. Tavaszi Gábor (Miskolc, Földes F. G. IV. o. t., t.: Dolák Gabriella és Zsudel László). 8. Lencse Gábor (Győr, Révai M. G. III. o. t., t.: Jagudits György és Takács István). 9. Késmárki Szabolcs (Kecskemét, Bányai J. G. III. o. t., t.: Borsos Ferenc).
Elsőfokú dicséretet 7, másodfokú dicséretet 24 versenyző kapott.
 

III. kategória

 
1. díj: Miskolczi Norbert (Pécs, Leöwey K. G. IV. o. t., t.: Simai Margit)
2. díj; Hauer Tamás (Budapest, Apáczai Cs. J. G. IV. o. t., t.: Kelemen László)
3. díj: Csáki Csaba (Budapest, Apáczai Cs. J. G. IV. o. t., t.: Kelemen László)
 
A további helyezettek: 4. Walkensdorfer Péter (Székesfehérvár, József A. G. IV. o. t., t.: Perepatitsné Majorovics Margit). 5. Kullai Gábor (Budapest, Apáczai Cs. J. G. IV. o. t., t.: Zsigri Ferenc). 6. Rösner Vilmos (Budapest, Apáczai Cs. J. G. IV. o. t., t.: Kelemen László). 7. Bodrogi Péter (Miskolc, Földes F. G. IV. o. t., t.: Zámborszky Ferenc és Szepessy Zoltánné). 8. Kégl Balázs (Budapest, Apáczai Cs. J. G. IV. o. t., t.: Zsigri Ferenc). 9. Lakó Sándor (Kecskemét, Katona J. G. IV. o. t., t.: Szablics Bálint). 10. Kiss Tamás (Budapest, József A. G. IV. o. t., t.: Tóth Eszter).
Elsőfokú dicséretet 10, másodfokú dicséretet 18 versenyző kapott.