Kezdőlap


Cím:	Erők egyensúlya - energia minimuma (Megjegyzések B. J. Kogan cikkéhez)
Szerző(k):	Gnädig Péter
Füzet:	1988/január, 38 - 39. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

B. J. Kogan fenti cikke a geometria és a fizika bizonyos területei közt fennálló érdekes kapcsolatra hívja fel a figyelmet. Az általa felsorolt példák a háromszög bizonyos nevezetes vonalainak egy ponton való áthaladását "bizonyítják'' a fizika módszereivel. Ez a gondolatmenet azonban továbbvihető s egészen más jellegű geometriai feladatok is megoldhatók a mechanika törvényeinek alkalmazásával.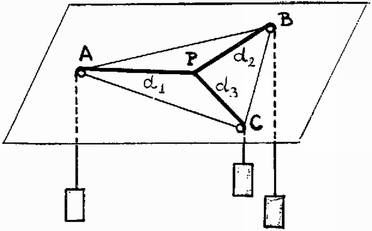
Ismeretes, hogy egy tömegpont csak olyan helyen lehet stabil egyensúlyi helyzetben, ahol a rá ható (konzervatívnak feltételezett) erőkhöz tartozó helyzeti energia minimális. Ha ugyanis lenne a vizsgált pontok közelében egy olyan hely, ahol még kisebb a test helyzeti energiája, akkor oda "szívesen'' menne, s a két energia különbségéből még mozgási energiára ‐ vagy a súrlódás legyőzésére ‐ is futná. Természetesen a minimumfeltétel csak a test által ténylegesen elérhető helyek összehasonlítását engedi meg. Ha kényszerek korlátozzák a test mozgását (például egy lejtős felületen mozoghat csak, vagy egy fonál nyújthatatlansága miatt egy adott ponttól mért távolsága meghatározott értékű kell legyen), akkor csak a kényszerek által meghatározott helyek közül választhatja ki a legkisebb helyzeti energiájú állapotot.
Másrészt viszont az egyensúlyi helyzetben a testre ható erők eredője, vagyis a vektori összege nulla kell legyen. Az egyensúly feltételének kétféle megfogalmazása lehetőséget kínál arra, hogy bizonyos geometriai szélsőértékfeladatokat más, néha egyszerűbb problémára vezessünk vissza. (Természetesen a fordított út is elképzelhető; a fizika nagyon sok törvénye megfogalmazható minimumfeladatként is.)
Itt most egyetlen példát mutatunk be az ilyen típusú feladatok széles választékából. Határozzuk meg egy általános háromszög azon belső pontját, amelyre a háromszög csúcspontjaitól mért távolságok összege minimális! Diszkutáljuk a megoldhatóság feltételét is.

1. ábra

Olyan fizikai helyzetet kell teremtenünk, amelyben valamilyen rendszer teljes helyzeti energiája arányos lesz azzal a mennyiséggel, amelynek minimumát keressük. Jelen esetben ezt úgy érhetjük el, hogy a háromszög csúcsaiba csigákat helyezünk, s ezeken keresztül három azonos tömegű testet lógatunk le. A fonalak egyik végét az ábrán látható módon összekötjük, a háromszöget (pontosabban a háromszöget realizáló testet) pedig vízszintes helyzetben rögzítjük. Amennyiben az egyes fonalak hossza

l_{1}

l_{2}

és

l_{3}

, a

P

pontnak a csúcsoktól mért távolsága pedig

d_{1}, d_{2}

és

d_{3}

, úgy a rendszer teljes helyzeti energiája (a háromszög síkjához képest)

\begin{matrix} E_{helyezeti} = - m g (l_{1} - d_{1}) - m g (l_{2} - d_{2}) - m g (l_{3} - d_{3}) = \\ = állandó + állandó \cdot (d_{1} + d_{2} + d_{3}) . \end{matrix}

A rendszer energiája akkor a legkisebb, ha a

d_{1} + d_{2} + d_{3}

minimális. Másrészt a fonalakat egyenlő nagyságú erők feszítik, s ezen erők csak úgy adhatnak nulla eredőt a

P

pontban, ha a fonalak

120^{\circ}

-os szöget zárnak be egymással. Ennek felismerése után a

P

pont tényleges helyzetének meghatározása nem nehéz; egy-egy

120^{\circ}

-os látószögű körív metszéspontja kijelöli a keresett pontot (2. ábra). Látható, hogy hegyesszögű háromszög esetén a feladat mindig egyértelműen megoldható, tompaszögű háromszögnél viszont elképzelhető, hogy a

120^{\circ}

-os látószögnek megfelelő körívek a háromszögön kívül metszik egymást. Ez akkor fordulhat elő, ha a háromszög egyik szöge

120^{\circ}

-nál nagyobb. Ilyenkor a minimumfeltételnek a háromszög tompaszögű csúcsa tesz eleget.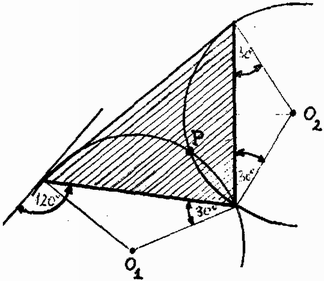

2. ábra

A feladat könnyen általánosítható. Amennyiben olyan pontot keresünk, melyre a csúcspontoktól mért távolságok súlyozott összege minimális, úgy nyilván különböző tömegű súlyokat kell a fonalak végeire akasztanunk s ezek egyensúlyának feltételét vizsgálnunk. Elemi geometriai úton meglehetősen bonyolult lenne a probléma megoldása.