Kezdőlap


Cím:	A mechanika alkalmazása a geometriában (Részlet)
Szerző(k):	B. J. Kogan
Füzet:	1988/január, 33 - 38. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ebben a cikkben néhány, a háromszögek geometriájához tartozó állítást igazolunk, mégpedig oly módon, hogy a bizonyításokban a statika alapfogalmaira, axiómáira, szabályaira támaszkodunk. Feltételezzük, hogy az Olvasó előtt ismeretes az erővektor fogalma és tulajdonságai; a merev testre ható erők összegzésének módja; egy test egyensúlyának feltétele; ... Ennek ellenére ‐ a későbbiekben játszott szerepére tekintettel ‐ kiemeljük, hogy
ha egy merev testre három, nem párhuzamos, egy síkban fekvő erő hat, és ezek egymással egyensúlyt tartanak, akkor hatásvonalaik egy pontban metszik egymást.

Bizonyításainkban lényegében ezt a megállapítást alkalmazzuk.

1. A háromszög szögfelezőire vonatkozó tétel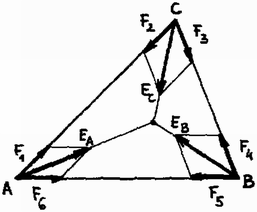

1. ábra

Tekintsük az 1. ábra szerint felvett, az

A B C

háromszög oldalegyenesei mentén ható, egyenlő nagyságú

F_{1}

F_{2}

...

F_{6}

erőket! Mivel ezek az erők nyilvánvalóan egyensúlyban vannak, eredőik, az ábrán látható

E_{A}

E_{B}

E_{C}

erők szintén egyensúlyban lesznek. Ezek az eredők viszont ‐ a háromszög csúcsainál keletkező rombuszok alapján ‐ a háromszög szögeinek belső szögfelezőire illeszkednek; következésképpen a háromszög belső szögfelezői egy pontban metszik egymást. Hasonló gondolatmenet alapján az Olvasó maga is könnyen beláthatja, hogy a háromszög két külső és egy belső szögfelezője egy ponton halad át.

2. A háromszög magasságaira vonatkozó tétel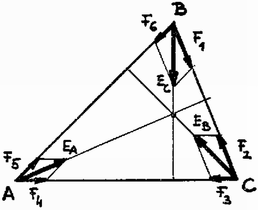

2. ábra

A 2. ábrán látható

A B C

háromszög oldalain úgy helyeztük el az

F_{1}

F_{2}

...

F_{6}

erőket, hogy egy tetszőleges

F

erő választása után az

\begin{matrix} \begin{matrix} F_{1} = F_{2} = F cos A \\ F_{3} = F_{4} = F cos B \\ és & F_{5} = F_{6} = F cos C \end{matrix}} \end{matrix}

(1)

összefüggések teljesüljenek, vagyis erőrendszerünk egyensúlyban legyen, azaz az erők páronként alkotott eredői egy ponton haladjanak át. Határozzuk meg ezen eredők irányát! Adjuk össze például a

B

csúcsban támadó

F_{1}

és

F_{6}

erőket! E célból bontsuk mindkettőt két összetevőre úgy, hogy ezek egyike az

A C

oldallal párhuzamosan, a másik rá merőlegesen helyezkedjen el!

3. ábra

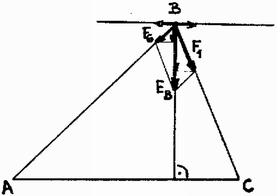A 3. ábra alapján látható, hogy

F_{1} A C

-vel párhuzamos összetevője

F_{1} cos C

-vel,

F_{6}

azonos állású összetevője pedig

F_{6} cos A

-val egyenlő. De az (1) összefüggésből következik, hogy

\begin{matrix} \frac{F_{1}}{F_{6}} = \frac{cos A}{cos C}, (derékszögű háromszögnél ez nem igaz) \end{matrix}

ahonnan

F_{1} cos C = F_{6} cos A

. Így

F_{1}

és

F_{6}

A C

-vel párhuzamos összetevői azonos nagyságúak és ellentétes irányúak, ezért összegük

0

. Ebből az következik, hogy

F_{1}

és

F_{6}

eredője az

A C

oldalra merőleges; ilyen módon az

E_{B}

erő hatásvonala az

A C

oldalhoz tartozó magassággal egyezik meg. Hasonló módon kaphatjuk, hogy az

E_{A}

és

E_{C}

erők hatásvonala a háromszög másik két magasságvonalával esik egybe; következésképpen a háromszög magasságvonalai egy pontban metszik egymást.

3. A háromszög súlyvonalaira vonatkozó tétel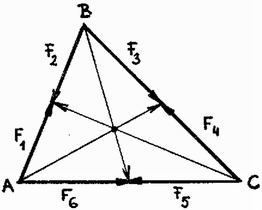

4. ábra

Tekintsük a 4. ábrán látható módon elhelyezett

F_{1}

F_{2}

...

F_{6}

erőket! Legyen mindegyik erővektor hossza a megfelelő háromszögoldal fele! Ekkor az

F_{1}

és

F_{6}

erők eredője a

B C

F_{2}

és

F_{3}

erők eredője az

A C, F_{4}

és

F_{5}

erőké pedig az

A B

oldalhoz tartozó súlyvonal mentén hat (lásd a megfelelő erőparalelogrammákat). Mivel pedig

F_{1}

F_{2}

...

F_{6}

egyensúlyban vannak, a háromszög súlyvonalai egy pontban metszik egymást.

4. A belső szögfelezőkre vonatkozó tétel általánosítása
Az

A B C

háromszögben vegyük fel az

A

szöget

α_{1}

és

α_{2}

részekre osztó

a

, a

B

szöget

β_{1}

és

β_{2}

részekre osztó

b

és a

C

szöget

γ_{1}

és

γ_{2}

részekre osztó

c

egyenest (5. ábra) !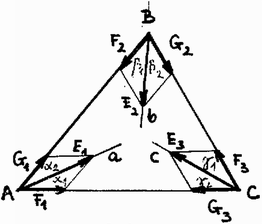

5. ábra

Helyezzünk el az

A

csúcsnál egy tetszőleges nagyságú,

a

-val azonos hatásvonalú

E_{1}

erőt, majd bontsuk fel a háromszög oldalai mentén

F_{1}

és

G_{1}

összetevőkre! Járjunk el hasonló módon a háromszög

B

és

C

csúcsánál is, ezzel együtt azonban

E_{2}

-t válasszuk úgy, hogy

F_{2}

egyenlő legyen

G_{1}

-gyel,

E_{3}

-at pedig úgy, hogy

F_{3}

nagysága egyenlő legyen

G_{2}

-vel! Így az

E_{1}

E_{2}

E_{3}

erőrendszerrel ekvivalens

F_{1}

G_{3}

rendszerhez jutunk.

Tekintsük a

\frac{sin α_{1}}{sin α_{2}}

\frac{sin β_{1}}{sin β_{2}}

és

\frac{sin γ_{1}}{sin γ_{2}}

arányokat!

A

B

és

C

csúcsoknál keletkezett paralelogrammák alapján

\begin{matrix} \frac{sin α_{1}}{sin α_{2}} = \frac{G_{1}}{F_{1}}, \frac{sin β_{1}}{sin β_{2}} = \frac{G_{2}}{F_{2}} valamint \frac{sin γ_{1}}{sin γ_{2}} = \frac{G_{3}}{F_{3}}, \end{matrix}

és ezért

\begin{matrix} \frac{sin α_{1}}{sin α_{2}} \cdot \frac{sin β_{1}}{sin β_{2}} \cdot \frac{sin γ_{1}}{sin γ_{2}} = \frac{G_{1}}{F_{1}} \cdot \frac{G_{2}}{F_{2}} \cdot \frac{G_{3}}{F_{3}} = \frac{G_{3}}{F_{1}} . \end{matrix}

(2)

A továbbiakban két eset lehetséges:
I.

\begin{matrix} \frac{sin α_{1}}{sin α_{2}} \cdot \frac{sin β_{1}}{sin β_{2}} \cdot \frac{sin γ_{1}}{sin γ_{2}} = 1, \end{matrix}

(3)

ekkor

F_{1} = G_{3}

, azaz az

F_{1}

és

G_{3}

erők, s így a velük ekvivalens

E_{1}

E_{2}

E_{3}

erők is egyensúlyban vannak, és ebből következik, hogy az

a

b

és

c

egyenesek egy pontban metszik egymást.
II.

\begin{matrix} \frac{sin α_{1}}{sin α_{2}} \cdot \frac{sin β_{1}}{sin β_{2}} \cdot \frac{sin γ_{1}}{sin γ_{2}} \neq 1, \end{matrix}

ekkor (2) szerint

F_{1} \neq G_{3}

. Belátjuk, hogy ebben az esetben az

a

b

és

c

egyenesek nem metszhetik egy pontban egymást. Tegyük fel ennek ellenkezőjét!
Ebben az esetben az

E_{1}

E_{2}

és

E_{3}

erőket hatásvonaluk közös

O

pontjába helyezve megkereshetjük eredőjüket

(E)

, amely ekvivalens kell legyen

F_{1}

és

G_{3}

eredőjével. Ez azonban nem lehetséges, mert az

F_{1}

és a

G_{3}

erők eredője az

A C

egyenesen fekszik,

E

hatásvonala pedig biztosan különbözik ettől, hiszen

O

nem eleme ennek az egyenesnek. A kapott ellentmondás azt mutatja, hogy az

a

b

és

c

egyenesek nem egy ponton haladnak át.
Ezek szerint az 5. ábrán látható egyenesek csak akkor metszik egymást egy pontban, ha fennáll a (3) összefüggés. Másképpen szólva: annak, hogy

a

b

és

c

egyenesek egy pontban messék egymást, szükséges és elégséges feltétele, hogy (3) teljesüljön. Ezt az állítást a belső szögfelezőkre vonatkozó tétel általánosításának tekinthetjük, hiszen ott nem csak (3) bal oldala, hanem a

\frac{sin α_{1}}{sin α_{2}}

\frac{sin β_{1}}{sin β_{2}}

\frac{sin γ_{1}}{sin γ_{2}}

arányok bármelyike is 1-gyel egyenlő.
Eredményünkből levezethető a háromszög magasságaira mondott tétel is; javasoljuk, hogy ezt az Olvasó végezze el önállóan.

5. A súlyvonalakra vonatkozó tétel általánosítása, Ceva tétele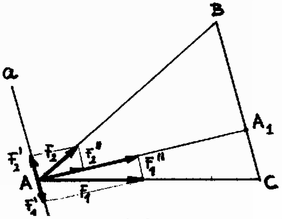

6. ábra

Tekintsük az

A B C

háromszöget! Legyen

F_{1}

és

F_{2}

erők hatásvonala

A B

és

A C

, eredőjük hatásvonala pedig

A A_{1}

(6. ábra)! Vegyük fel a

B C

oldallal párhuzamos,

A

-n áthaladó

D E

egyenest, és bontsuk fel az

F_{1}

erőt

F'_{1}, F''_{1}

; az

F_{2}

erőt

F'_{2}

és

F''_{2}

összetevőkre! Az ábra alapján

\begin{matrix} \frac{F'_{1}}{F_{1}} = \frac{A_{1} C}{A C} és \frac{F'_{2}}{F_{2}} = \frac{B A_{1}}{A B}, \end{matrix}

ahonnan

\begin{matrix} F'_{1} = F_{1} \cdot \frac{A_{1} C}{A C} és F'_{2} = F_{2} \cdot \frac{B A_{1}}{A B} . \end{matrix}

Mivel

F_{1}

és

F_{2}

erők eredőjének hatásvonala megegyezik

A A_{1}

-gyel,

F'_{1} = F'_{2}

. Következésképpen

\begin{matrix} F_{1} \cdot \frac{C A_{1}}{C A} = F_{2} \cdot \frac{B A_{1}}{A B} vagy \frac{F_{1}}{F_{2}} = \frac{C A}{A B} \cdot \frac{B A_{1}}{C A_{1}} . \end{matrix}

(4)

7. ábra

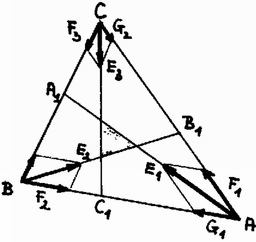Vegyük most az

A B C

háromszög oldalain az

A_{1}

B_{1}

C_{1}

pontokat, és kössük össze őket a szemközti csúcsokkal (7. ábra)! Helyezzük el az

A

B

és

C

pontokban támadó

E_{1}

E_{2}

és

E_{3}

erőket úgy, hogy hatásvonalaik az

A A_{1}

B B_{1}

és

C C_{1}

egyenesek legyenek, majd bontsuk fel őket olyan összetevőkre, melyek a háromszög oldalaira esnek! Mindemellett

E_{1}

-et válasszuk tetszőlegesen, az

E_{2}

és

E_{3}

erőket pedig úgy, hogy

\begin{matrix} F_{2} = G_{1} és F_{3} = G_{2} \end{matrix}

(5)

teljesüljön! Továbbá (4) szerint

\begin{matrix} \frac{F_{1}}{G_{1}} = \frac{C A}{A B} \cdot \frac{B A_{1}}{A_{1} C}, \frac{F_{2}}{G_{2}} = \frac{A B}{B C} \cdot \frac{C B_{1}}{B_{1} A} és \frac{F_{3}}{G_{3}} = \frac{B C}{C A} \cdot \frac{A C_{1}}{C_{1} B} . \end{matrix}

Ezen egyenlőségek szorzatát képezve kapjuk, hogy

\begin{matrix} \frac{F_{1}}{G_{1}} \cdot \frac{F_{2}}{G_{2}} \cdot \frac{F_{3}}{G_{3}} = \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} \cdot \frac{A C_{1}}{C_{1} B}, \end{matrix}

majd a tényezők sorrendjének változtatásával és (5) figyelembe vételével kapjuk, hogy:

\begin{matrix} \frac{A C_{1}}{C_{1} B} \cdot \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} = \frac{F_{1}}{G_{3}} . \end{matrix}

(6)

Vizsgáljuk az alábbi két esetet:
I.

\begin{matrix} \frac{A C_{1}}{C_{1} B} \cdot \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} = 1. \end{matrix}

(7)

Ekkor

F_{1} = G_{3}

, azaz ezek az erők egyensúlyban vannak; következésképpen

E_{1}

E_{2}

és

E_{3}

is, tehát az

A A_{1}

B B_{1}

és

C C_{1}

egyenesek egy pontban metszik egymást.
II.

\begin{matrix} \frac{A C_{1}}{C_{1} B} \cdot \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} \neq 1. \end{matrix}

Ekkor (6) szerint

F_{1}

és

G_{3}

különbözőek. Az előző tétel bizonyításakor említett gondolatmenet alapján arra a következtetésre juthatunk, hogy az

A A_{1}

B B_{1}

és

C C_{1}

egyenesek nem haladhatnak át egy ponton.
Így annak, hogy az

A A_{1}

B B_{1}

és

C C_{1}

egyenesek egy pontban messék egymást, szükséges és elégséges feltétele, hogy fennálljon a (7) egyenlőség. Most bizonyított tételünk Ceva nevét viseli, és ennek valóban speciális esete a súlyvonalakról szóló tétel, hiszen abban az esetben

\begin{matrix} \frac{A C_{1}}{C_{1} B} = \frac{B A_{1}}{A_{1} C} = \frac{C B_{1}}{B_{1} A} = 1. \end{matrix}

Ceva tétele, csakúgy, mint az előző pontban bizonyított tétel, kiterjeszthető arra az esetre, amikor a vizsgált egyenesek a háromszögön kívül metszik egymást.
A mechanika geometriai alkalmazásait érintő kirándulásunkat ezzel befejeztük, csupán az érdekesség kedvéért megemlítjük, hogy szintén statikai megfontolásokkal igazolható többek között Pitagorász-tétele vagy a körlemez egy pontján áthaladó szelőkre vonatkozó tétel.