Cím:	Az 1988. évi Arany Dániel Matematiaki Verseny feladatai
Füzet:	1988/november, 356 - 359. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. forduló   Kezdők (legfeljebb I. osztályosok)   1. Ábrázolja derékszögű koordináta-rendszerben azoknak a pontoknak a halmazát, melynek koordinátáira $||x-3|-1|<y\leqq 2$ teljesül.   2. Hosszabbítsa meg egy szabályos hatszög minden oldalát a saját hosszával (egy meghatározott körüljárási irányt tartva). A végpontok összekötésével nyert új hatszög területe hányszorosa az eredetinek?   3. Adott három, különböző pozitív számjegy. Képezze e három számjegyből az összes lehetséges ‐ különböző számjegyekből álló ‐ egy, két és háromjegyű számot, és adja ezeket össze. Lehet-e az összeg a) $1988$; b) $2000$?   4. Melyik nagyobb: $\begin{array}{c}{\displaystyle {1988}^{1988}\text{ vagy }{1987}^{1987}+{1988}^{1987}+{1987}^{1988}?}\end{array}$   5. Adott a síkon két egymásra merőleges egyenes, $e$ és $f$, egy $C$ pont és egy $d$ távolság. Szerkesszen olyan derékszögű háromszöget, melynek derékszögű csúcsa a $C$ pont, átfogója $d$ hosszúságú és az átfogó egy-egy végpontja az $e$, illetve $f$ egyenesen van.   6. Gondoltam egy számot. Ha $7$-tel osztom, a maradék $6$; ha $4$-gyel osztom, a maradék $1$. Mennyi a maradék, ha $28$-cal osztom?   7. Oldja meg az $\left[||\left[x\right]|-\left[|x|\right]|\right]=0$ egyenletet! ($\left[z\right]$ a $z$ szám egészrészét jelenti, azt a legnagyobb egész számot, ami nem nagyobb $z$-nél.)   8. Legyen $n$ (tízes számrendszerben) legalább $k$ jegyű természetes szám. Igazolja, hogy az alábbi állítások ekvivalensek! a) $n^4$ utolsó $k$ db jegye azonos $n$ utolsó $k$ db jegyével. b) $n^2$ utolsó $k$ db jegye azonos $n$ utolsó $k$ db jegyével.   Haladók (II. osztályosok)   1. Határozzuk meg a valós számok halmazának azt a legbővebb részhalmazát, amelyen az $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{\sqrt[]{\sqrt[]{2}x-x\sqrt[]{x-2}}}{\sqrt[]{\sqrt[]{x}-2}+1}}\end{array}$ függvény értelmezhető.   2. Van-e olyan háromszög, melynek két oldala $1$ és $4\text{cm}$, valamely két magassága pedig $3$ és $4\text{cm}$ hosszú? 3. Hány téglalap jelölhető ki a rajzon látható $4\times 10$-es rács vonalaival?     4. A $p$ prímszám (a tízes számrendszerben felírva) páros sok jegyet tartalmaz. Ha a $p$ számot fordított sorrendben írjuk fel, visszakapjuk saját magát. Határozzuk meg $p$-t.   5. Az $ABC$ derékszögű háromszögbe írt négyzet két csúcsa az $AB$ átfogón, másik két csúcsa pedig a befogókon van. Mekkora a befogók aránya, ha a négyzet $K$ középpontjára igaz, hogy $CAB\sphericalangle =ABK\sphericalangle$?   6. Legyenek $x$ és $y$ valós számok. Tudjuk, hogy az $x+y$, $x-y$, $xy$, $\frac{x}{y}$ számok egyike sem $0$ és közülük három racionális. Mutassuk meg, hogy $x$ és $y$ racionális számok.   7. Tetszőleges számú egységnyi, illetve két egységnyi oldalú négyzet áll rendelkezésünkre. Bizonyítsuk be, hogy kiválasztható $1987$ darab úgy, hogy belőlük ki lehessen rakni egy négyzetet (hézagtalanul és egyrétűen); viszont bárhogyan is választunk ki $1988$ darabot, azokból sohasem állítható elő négyzet.   8. Az $a$, $b$, $c$ valós számok olyanok, hogy $|a{x}^2+bx+c|\leqq 1$, ha $|x|\leqq 1$. Mutassuk meg, hogy$|x|\leqq 1$ esetén $|c{x}^2-bx+a|\leqq 4$ is teljesül.   II. forduló   Kezdők (legfeljebb I. osztályosok)   A szakközépiskolások feladatai   1. A $2bx+b=3cx+c$ egyenletben $b$ is és $c$ is az $1;2;\text{...};9$ értékeket veheti fel. Melyik $b$, $c$ számpárokra lesz az egyenlet gyöke pozitív?   2. Szerkessze meg az $ABCD$ paralelogrammát, ha adott az $AC$ átló, valamint a sík egy adott $P$ pontjának a csúcsoktól mért távolsága ($PA$, $PB$, $PC$, $PD$).   3. Adja meg bármely $n$ pozitív egész számra az $1^n+2^n+3^n+4^n$ szám utolsó számjegyét.   Az általános tantervű osztályok feladatai   1. Az $ABC$ hegyesszögű háromszög $A$-hoz tartozó magasságának talppontja $A\text{'}$, $B$-hez tartozó magasságának talppontja $B\text{'}$, a magasságpont $M$. Bizonyítsa be, hogy az $MC$, $B\text{'}A\text{'}$, $AB$ szakaszok felezőpontjai egy egyenesre esnek!   2. Egy hálózat $6$ pontból és $10$ élből áll. A hat pont egy szabályos ötszög öt csúcsa és középpontja. Az élek az ötszög oldalélei valamint a középpontból a többi csúcsba vezető sugarak. Minden ponthoz egy-egy valós számot rendelünk. Egy él teljesítményének nevezzük az él két végpontjába írt számok különbségének a négyzetét. Legyen a középpontba írt szám $0$, egy másik pontba írt szám $1$. Határozza meg a fennmaradó négy pontba írt számot úgy, hogy a tíz él teljesítményének összege minimális legyen.   3. $a_1<a_2<\text{...}<a_n<\text{...}$ pozitív páratlan számok. Bizonyítsa be, hogy van olyan négyzetszám $\left(k^2\right)$, amelyre $\begin{array}{c}{\displaystyle a_1+a_2+\text{...}+a_n\leqq k^2\leqq a_1+a_2+\text{...}+a_n+a_{n+1}!}\end{array}$   A speciális matematika tantervű osztályok feladatai   1. Osszuk fel a síkot egy körvonallal, egy téglalappal és egy háromszögvonallal a lehető legtöbb tartományra! Hány rész érhető el?   2. $a_1<a_2<\text{...}<a_n<\text{...}$ pozitív páratlan számok. 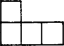Bizonyítsa be, hogy van olyan négyzetszám $\left(k^2\right)$, amelyre $\begin{array}{c}{\displaystyle a_1+a_2+\text{...}+a_n\leqq k^2\leqq a_1+a_2+\text{...}+a_n+a_{n+1}!}\end{array}$ 3. Milyen téglalap alakú sakktáblák fedhetők le egyrétűen az ábrán látható egybevágó alakzatokkal?       Haladók (II. osztályosok)   A szakközépiskolások feladatai   1. Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle x-x^3+x^5-x^7+x^9-x^{11}+x^2-x^4+x^6-x^8+x^{10}=1.}\end{array}$ 2. A különböző sugarú $k_1$ és $k_2$ körök az $A$ és $B$ pontokban metszik egymást. A körökön kívüli $P$ pontot összekötöttük az $A$ és $B$ pontokkal. A $PA$ és $PB$ egyenes a köröket további $C$, $D$, $E$ és $F$ pontokban metszi (lásd az ábrát). Bizonyítsuk be, hogy $PC\cdot PD\cdot P{A}^2=PE\cdot PF\cdot P{B}^2$. ($PC$, $PD$ stb.... a szakaszok hosszát jelöli.)     3. Az $n$ természetes szám olyan, hogy $2n+1$ és $3n+1$ is négyzetszám. Bizonyítsuk be, hogy $n$ osztható $8$-cal.   Az általános tantervű osztályok feladatai   1. Az $ABC$ háromszög magasságpontja $M$. Tudjuk, hogy $AB=CM$. Mekkora lehet a háromszög $C$ csúcsnál levő szöge?   2. Az $x^2+p_{1}x+q_1=0$ és az $x^2+p_{2}x+q_2=0$ másodfokú egyenletek együtthatói egészek. Tudjuk, hogy az egyenleteknek van olyan közös gyöke, amely nem egész szám. Bizonyítsuk be, hogy $p_1=p_2$, $q_1=q_2$.   3. Egy gulyában két falu $65$ tehene legel, vörösek, fehérek, feketék és tarkák. Igazoljuk, hogy ha nincsen öt különböző korú, azonos színű tehén a gulyában, akkor található három azonos színű és egyidős tehén ugyanabból a faluból.   A speciális matematika tantervű osztályok feladatai   1. Bizonyítsuk be, hogy minden $x$ pozitív valós számra teljesül az $\begin{array}{c}{\displaystyle {\left(\frac{1}{2^x}\right)}^{1+\frac{2}{x}}+{\left(1-\frac{1}{2^{x+1}}\right)}^{1+\frac{2}{x}}<1}\end{array}$ egyenlőtlenség.   2. Az $ABC$ hegyesszögű háromszög $M$ magasságpontjának az $A$, $B$, $C$ csúcsoktól vett távolsága rendre $x$, $y$, $z$. Bizonyítsuk be, hogy $abc=ayz+xbz+xyc$, ahol $a$, $b$, $c$ rendre a háromszög $A$, $B$, $C$ csúcsaival szemközti oldalainak hosszát jelöli.   3. Adott a síkon véges sok párhuzamos oldalú téglalap úgy, hogy bármely $k+1$ között található két olyan, melynek van közös pontja. Mutassuk meg, hogy megadható $k^2$ darab pont, melyek közül bármely téglalap tartalmaz legalább egyet.