1. $a$, $b$, $c$, $d$ különböző pozitív egész számok, amelyekre teljesül az

1,5;2,,3 számpárok megfelelnek a feltételeknek.

 

Megjegyzés. Miután megállapítottuk, hogy $a=1$, érdekes befejezés a következő: az

$\begin{array}{c}{\displaystyle 1+b=cd\mathrm{,}b=c+d}\end{array}$

egyenlőségekből a másodikat $c$-vel szorozva és az elsőt felhasználva

$\begin{array}{c}{\displaystyle bc=c^2+1+b\mathrm{.}}\end{array}$

Az egyenlőséget $4$-gyel szorozva így alakítjuk át:

$\begin{array}{c}{\displaystyle 4c^2-4bc+b^2+8=b^2-4b+\mathrm{4,}\text{ azaz }{\left(2c-b\right)}^2+8={\left(b-2\right)}^2\mathrm{.}}\end{array}$

A négyzetszámok közül csak az $1$ és a $9$ különbsége $8$, tehát $|2c-b|=1$, $|b-2|=3$, és innen ismét megkapjuk az előbbi két számpárt.

 

IV. megoldás. A feltételi egyenletekből következik, hogy

$\begin{array}{c}{\displaystyle \frac{ab}{a+b}=\frac{c+d}{cd}\mathrm{.}}\end{array}$

Mind a két tört pozitív , s így vagy $\frac{ab}{a+b}$ is, $\frac{c+d}{cd}$ is $1$, vagy az egyik, mondjuk az első, kisebb $1$-nél, a második nagyobb nála. Az első esetben $ab=a+b$, amiből $\left(a-1\right)\left(b-1\right)=1$, s így ‐ pozitív egész számokról lévén szó ‐ $a=b=2$. Ezek azonban nem különbözők.
A második esetben $ab<a+b$, és mivel egész számokról van szó,

$\begin{array}{c}{\displaystyle ab\le a+b-\mathrm{1,}\text{ azaz }\left(a-1\right)\left(b-1\right)\le 0.}\end{array}$

A bal oldal nem lehet negatív, tehát $0$ az értéke, vagyis az egyik szám, mondjuk $a=1$.
Ekkor

$\begin{array}{c}{\displaystyle cd=1+b=1+1\cdot b=1+c+d\mathrm{,}}\end{array}$

amiből $c$-t kifejezve

$\begin{array}{c}{\displaystyle c=\frac{d+1}{d-1}=1+\frac{2}{d-1}\mathrm{.}}\end{array}$

Mivel $c$ egész, így $d$ csak $2$ vagy $3$ lehet, $c$ megfelelő értékei pedig $3$ ill. $2$. Ezzel ismét az $\mathrm{1,}5$ és $\mathrm{2,}3$ számpárokhoz jutottunk.

 

2. Van-e a térben olyan ponthalmaz, amelynek minden síkon van pontja, de egyetlen síkon sincs végtelen sok pontja?

 

I. megoldás: Van ilyen ponthalmaz és nagyon sokféleképpen lehet ilyent megadni. Egy derékszögű koordinátarendszerben a pont koordinátáit $x$, $y$, $z$-vel jelölve minden sík egyenlete írható

$\begin{array}{c}{\displaystyle ax+by+cz+d=0}\end{array}$

alakban, ahol $a$, $b$, $c$ közt van $0$-tól különböző. A ponthalmazt úgy adjuk meg, hogy minden valós $t$ értékhez hozzárendeljük azt a pontot, amelyiknek koordinátái

$\begin{array}{c}{\displaystyle x=f\left(t\right)\mathrm{,}y=g\left(t\right)\mathrm{,}z=h\left(t\right)\mathrm{.}}\end{array}$

Az $f$, $g$, $h$ függvényeket úgy kell választanunk, hogy az

$\begin{array}{c}{\displaystyle af\left(t\right)+bg\left(t\right)+ch\left(t\right)+d=0}\end{array}$

egyenletnek legyen legalább egy gyöke, ha $a$, $b$, $c$ közül legalább az egyik nem $0$, de mindig csak véges sok gyöke legyen.
Kézenfekvő polinomokat választani, mert tudjuk, hogy egy polinomnak csak véges sok gyöke lehet: legfeljebb annyi, mint a foka, kivéve természetesen a $0$ polinomot. Azt is tudjuk továbbá, hogy (valós együtthatós) páratlan fokú polinomnak mindig van legalább egy (valós) gyöke. Ezek alapján az $x=t^5$, $y=t^3$, $z=t$ összefüggésekkel jellemzett ponthalmaz megfelel. Ezt írhatjuk kicsit egyszerűbben

$\begin{array}{c}{\displaystyle x=z^5\mathrm{,}y=z^3}\end{array}$

alakban is. Valóban, az

$\begin{array}{c}{\displaystyle a{z}^5+b{z}^3+cz+d=0}\end{array}$

egyenlet a mondott feltételek mellett mindig páratlan: $5$-öd-, $3$-ad- vagy elsőfokú, így a ponthalmaznak minden síkkal legalább egy és legfeljebb $5$ közös pontja van.

 

Megjegyzések. 1. Mint a megoldás is utal rá, $f$, $g$, $h$-nak bármilyen három különböző, páratlan fokú polinomot választhatunk. Használhatunk páros fokú polinomot is alkalmas előjel-megállapodásokkal kombinálva. Könnyű látni pl., hogy a következő ponthalmaznak:

$\begin{array}{c}{\displaystyle z=x^3\mathrm{,}y=\{{\displaystyle \begin{array}{c}\hfill {\displaystyle x^2\mathrm{,}\text{ ha }x\ge \mathrm{0,}}\\ \hfill {\displaystyle -x^2\text{ ha }x<0}\end{array}}}\end{array}$

szintén van pontja minden síkon és mindegyiken csak véges számú. Belátható, hogy ennek is legfeljebb $5$ pontja lehet egy síkon. Ennek igazolását az olvasóra bízzuk.

 

2. A megadott ponthalmazok pontjai térbeli görbét alkotnak. Az előző megjegyzésben szereplő görbéhez eljuthatunk úgy, hogy az $x$- és $z$-tengely síkjában megrajzoljuk a $z=x^3$ egyenletű görbét, és tekintjük az ennek a pontjain át az $y$ tengellyel párhuzamosan húzott egyenesek alkotta (általános) hengerfelületet; az $y$- és $x$-tengely síkjában pedig az origóban érintkező, első, ill. harmadik negyedben futó két félparabolaívből álló görbe pontjain át a $z$-tengellyel párhuzamosan húzott egyenesek alkotta hengerfelületet képezzük. A két felület metszésvonala adja a szóban forgó görbét ( 1. a, b, c ábra).

 

 

1.a ábra

 

 

 

1.b ábra

 

 

 

1.c ábra

 

3. Használhatók polinomok helyett más függvények is. Erre mutat példát a következő megoldás.

 

II. megoldás. Három térbeli görbe vonalat adunk meg, amelyek egyesítésére teljesülnek a követelmények. Ezek szemléletesen így származtathatók. Egy $2\pi$ szélességű végtelen sáv középvonala legyen az ordinátatengely. Ábrázoljuk a $\text{tg<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}$ függvényt a $-\pi <\phi <\pi$ számközben ( 2.a ábra), majd hajlítsuk össze a sávot egy (egységnyi sugarú) hengerré. A henger három példányát helyezzük el úgy, hogy a tengelyük rendre az $x$-, $y$-, $z$-tengely legyen, a sáv ($\mathrm{0,0}$) pontja pedig az $y$-, $z$-, illetőleg $x$-tengely egységpontjába kerüljön. (A 2.b ábra a harmadik hengert ábrázolja.)

 

 

2.a ábra

 

 

 

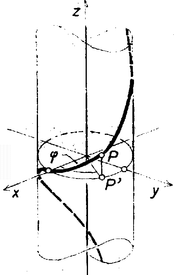2.b ábra

 

A feltételek teljesülésének igazolásához célszerű a pontok koordinátáit formulákkal megadni. A $z$-tengely körüli henger egy pontja legyen $P$, vetülete az $x$, $y$ koordinátasíkon $P\text{'}$, az ehhez mutató vektornak az $x$-tengely pozitív felével bezárt szöge $\phi$. Ekkor az ($1$, $0$, $0$) ponttól $P\text{'}$-ig terjedő körív hossza is $\phi$, így a $P$ pont koordinátái:

$\begin{array}{c}{\displaystyle x=\text{cos}\phi \mathrm{,}y=\text{sin}\phi \mathrm{,}z=\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>.}}\end{array}$

A másik két görbe pontjainak koordinátái:
${\displaystyle \begin{array}{c}\hfill {\displaystyle x=\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>, y=<span style="font-weight: normal;font-style: normal;">cos</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>, z=<span style="font-weight: normal;font-style: normal;">sin</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>, ill.<br> x=<span style="font-weight: normal;font-style: normal;">sin</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>, y=}\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>, z=<span style="font-weight: normal;font-style: normal;">cos</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>; }}\hfill \end{array}}$

$\phi$ mindhárom esetben $-\pi$ és $\pi$ közti szöget jelent (radiánban mérve).
Egy tetszés szerinti sík egyenlete

$\begin{array}{c}{\displaystyle ax+by+cz+d=0}\end{array}$

(1)

alakú, ahol $a$, $b$, $c$ közt van $0$-tól különböző. Ennek a harmadik görbével való metszéspontjai azok a pontok, amelyek koordinátái az

$\begin{array}{c}{\displaystyle a\text{cos}\phi +b\text{sin}\phi +c\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>+d = 0}}\end{array}$

egyenletnek eleget tévő $\phi$ értékekhez az első egyenlethármassal meghatározott értékek.
Az egyenlet $t=\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}$-re vonatkozó algebrai egyenletté alakítható a következő összefüggések felhasználásával:
${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}\phi =\frac{2\text{sin}\frac{\phi }{2}\text{cos}\frac{\phi }{2}}{\text{sin}{}^2\frac{\phi }{2}+\text{cos}{}^2\frac{\phi }{2}}=\frac{2t}{t^2+1};}\hfill \\ \hfill {\displaystyle \text{cos}\phi =\frac{\text{cos}{}^2\frac{\phi }{2}-\text{sin}{}^2\frac{\phi }{2}}{\text{sin}{}^2\frac{\phi }{2}+\text{cos}{}^2\frac{\phi }{2}}=\frac{1-t^2}{1+t^2}\mathrm{.}}\hfill \end{array}}$

Ezeket beírva, a törteket eltávolítva és az egyenletet rendezve kapjuk, hogy:

$\begin{array}{c}{\displaystyle c{t}^3+\left(d-a\right)t^2+2bt+a+d=0.}\end{array}$

(2)

Ennek legfeljebb $3$ megoldása van (a valós számok körében), kivéve, ha az azonosan $0$ polinomról van szó, vagyis ha

$\begin{array}{c}{\displaystyle b=c=d-a=a+d=0.}\end{array}$

Ekkor azonban $a$ és $d$ is $0$, s így az (1) egyenlet minden ($x$, $y$, $z$) számhármasra teljesül, nem sík egyenlete. Mivel $\text{tg<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>φ</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}$ a $-\pi <\phi <\pi$ számközben minden valós értéket felvesz, és mindegyiket csak egyszer, így a síknak a görbével legfeljebb $3$ közös pontja lehet.
Ugyanígy adódik, hogy egy síknak a másik két görbével is legfeljebb $3$-$3$ közös pontja lehet, az egész ponthalmazzal tehát legfeljebb $9$.
Az is világos, hogy minden síknak van közös pontja a halmazzal, mert ha pl. $c\ne 0$, akkor a (2) egyenlet harmadfokú és így van valós gyöke.

 

Megjegyzések. 1. Szemléletesen a hengert elmetszettük egy síkkal, és azt kérdezzük, hogy ha a hengerfelületet egy alkotója mentén felvágjuk és a síkba terítjük, a metszésvonal hány pontban metszi a tangensgörbe képét. Belátjuk, hogy ha a sík metszi a henger tengelyét, de nem merőleges rá, akkor a metszésvonal a síkba terítve egy szinuszvonalat ad.
Valóban, a henger egy tetszés szerinti pontjának koordinátái $x=\text{cos}\phi$, $y=\text{sin}\phi$, $z$ alakban írhatók, így az (1) síkkal való metszéspontokat azok a $\phi$ értékek szolgáltatják, amelyekre

$\begin{array}{c}{\displaystyle a\text{cos}\phi +b\text{sin}\phi +cz+d=0.}\end{array}$

A síkra kimondott feltételek akkor teljesülnek, ha $c$, továbbá $a$ és $b$ közül legalább az egyik nem $0$. Ekkor egyenletünk így alakítható át:

$\begin{array}{c}{\displaystyle z=-\frac{a}{c}\text{cos}\phi -\frac{b}{c}\text{sin}\phi -\frac{d}{c}=\frac{\sqrt[]{a^2+b^2}}{c}\text{sin}\left(\phi -\alpha \right)-\frac{d}{c}\mathrm{,}}\end{array}$

ahol $\alpha$-t a

$\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{-a}{\sqrt[]{a^2+b^2}}\mathrm{,}\text{cos}\alpha =\frac{b}{\sqrt[]{a^2+b^2}}}\end{array}$

összefüggések határozzák meg. Ezzel a kimondott állítást igazoltuk. A fenti meggondolás azt a szemléleti megfigyelést igazolja, hogy a két vonalnak legfeljebb $3$ metszéspontja lehet.

 

2. Megfelelő ponthalmazok számtalan más elgondolás alapján is elkészíthetők, és merült is fel sok további példa a dolgozatokban. Többen állították azonban azt is, egyesek indokolni is próbálták, hogy a kívánt tulajdonságú ponthalmaz nem létezik.

 

3. A felmerült példák mindegyikében volt olyan sík, amelyik a ponthalmaznak legalább $5$ pontját tartalmazta. Kézenfekvő kérdés, hogy nem adható-e meg olyan ponthalmaz, amelyiknek minden síkon $5$-nél kevesebb pontja van. Nem csökkenthető ez a szám $3$ alá, hiszen a halmaz bármely $3$ pontján át fektethető sík. Mély halmazelméleti módszerekkel bebizonyítható, hogy létezik olyan ponthalmaz is, amelyiknek minden síkon pontosan $3$ pontja van. Ez a bizonyítás azonban csupán a ponthalmaz létezését adja, előállításához vagy egyáltalán az elképzeléséhez sem ad semmilyen támpontot.
Megmutatható, hogy egy folytonos vonalnak, ha kielégíti a feltételeket, mindig van $5$ egy síkban lévő pontja.

 

3. Egy $3n+1$ tagú társaság bármely két tagja vagy teniszezni, vagy sakkozni, vagy pingpongozni szokott egymással. Mindegyiküknek $n$ tenisz-, $n$ sakk- és $n$ pingpongpartnere van.
Bizonyítsuk be, hogy van a társaságban három olyan ember, akik egymás között mind a három játékot játsszák.

 

I. megoldás. Mindenki mindenkivel csak egyféle játékot játszik, hiszen mindenkinek $3n$ partnere van és összesen ennyi játszmában vesz részt.
Három embert összesen

$\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{3n+1}{3}\right)}\end{array}$

-féleképpen lehet kiválasztani a társaságból. Számoljuk össze, hány olyan hármas lehet maximálisan, amelyiknek a tagjai legfeljebb kétféle játékot játszanak egymás közt! A társaság egy $A$ tagja $n$ emberrel pingpongozik, így $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ olyan hármasban van benne, amelyiknek mind a két másik tagjával pingpongozik. Ugyanennyi olyan hármasban van benne, amelyikben mindkét partnerrel sakkozik, illetőleg amelyikben mindkettővel teniszezik, tehát $3\cdot \left(\genfrac{}{}{0ex}{}{n}{2}\right)$ olyan hármas van, amelyikben ő csak egyféle játékot játszik. Ez igaz a társaság bármelyik tagjára, tehát az olyan hármasok száma, amelyeknek tagjai legfeljebb kétféle játékot játszanak egymás közt, nem több, mint

$\begin{array}{c}{\displaystyle 3\left(\genfrac{}{}{0ex}{}{n}{2}\right)\left(3n+1\right)\mathrm{,}}\end{array}$

az olyan hármasokat ugyanis, ha vannak, amelyeken belül csak egyféle játékot játszanak, többször vettük számba. Az olyan hármasok száma tehát, amelyeken belül mind a három játékot játsszák, legalább

$\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{3n+1}{3}\right)-3\left(\genfrac{}{}{0ex}{}{n}{2}\right)\left(3n+1\right)=\frac{\left(3n+1\right)3n\left(3n-1\right)}{6}-3\frac{n\left(n-1\right)}{2}\cdot \left(3n+1\right)=3n^2+n\mathrm{.}}\end{array}$

A feladat állítása tehát igaz.

 

Megjegyzés. A bizonyítás alsó korlátot is adott a feladat követelményeit kielégítő hármasok számára, nem adott viszont eljárást ilyen hármasok kiválasztására, csak létezésüket bizonyítja.

 

II. megoldás. A feladat állításának helyességét indirekt úton bizonyítjuk. Legyen $A$ a társaság egy tagja, $\text{P}$ azoknak a csoportja, akik $A$-val pingpongoznak, $\text{S}$ azoké, akik sakkoznak vele és $\text{T}$ az $A$-val teniszezőké. Tegyük fel, hogy nincs a feladat állításának megfelelő hármas. Ekkor egy $\text{P}$-beli és egy $\text{S}$-beli nem teniszezhet, egy $\text{S}$-beli és egy $\text{T}$-beli nem pingpongozhat, egy $\text{T}$-és egy $\text{P}$-beli pedig nem sakkozhat, mert különben $A$-val megfelelő hármast alkotnának.
Megszámoljuk kétféleképpen azoknak a hármasoknak a számát, amelyekben mindegyik csoportnak egy tagja szerepel. Mindegyik csoportból $n$-féleképpen választhatunk egy embert, tehát a lehetséges hármasok száma $n^3$. Mivel egyik hármas tagjai sem játsszák mind a három játékot egymás közt, így valaki mindkét partnerével ugyanazt a játékot játssza. Egy ilyen hármas $\text{P}$-beli tagja mindkét partnerével csak pingpongot játszhat fenti megállapításaink szerint. Ha $\text{S}$-ből $j$ emberrel pingpongozik, $\text{T}$-ből pedig $k$-val, akkor $jk$ olyan hármasnak tagja, amelyiken belül két pingpongozó pár van. Egyrészt tudjuk, hogy összesen $n$ pingpongpartnere van, így^{${}^{*}$} $j+k\le n$, másrészt a mértani és számtani közép közti egyenlőtlenség szerint

$\begin{array}{c}{\displaystyle jk\le {\left(\frac{j+k}{2}\right)}^2\le {\left(\frac{n}{2}\right)}^2\mathrm{.}}\end{array}$

Mivel a $\text{P}$ csoportnak $n$ tagja van, tehát legfeljebb $n^3/4$ olyan hármas van, amelyikben két pingpongozó pár szerepel. Ugyanez igaz az olyan hármasok számára is, amelyekben két sakkozó, ill. amelyekben két teniszező pár szerepel. Ez azonban összesen is csak $3n^3/4$ hármast ad, kevesebbet, mint az összes tekintetbe vett hármasok száma. Indirekt feltevésünk tehát helytelennek bizonyult, kell olyan hármasnak lennie, amelyiknek tagjai mindegyik játékot játsszák egymás közt.

 

III. megoldás. Tekintsük ismét a társaságnak az előző megoldásban szereplő felbontását csoportokra. Becsüljük meg felülről azoknak a hármasoknak a számát, amelyekben szerepel $A$, és amelyek nem felelnek meg a feladat állításában szereplő feltételnek. Csak olyan hármasok jönnek tekintetbe, amelyekben $A$-n kívül két különböző csoportbeli ember szerepel. Az ilyen hármasok száma $3n^2$. Azt is láttuk az előző megoldásban, hogy egy ilyen hármas akkor nem megfelelő, ha benne egy pingpongozó pár egyike $\text{P}$-ből való, vagy egy sakkparti egyik résztvevője $\text{S}$-ből, vagy egy teniszező pár egyike $\text{T}$-ből való. Egy $\text{P}$-beli $P$ személy $\text{S}$-ből és $\text{T}$-ből együtt legfeljebb $n-1$ emberrel pingpongozik, mert egyik pingpongpartnere $A$. A tekintetbe vett hármasok közül azok száma, amelyekben a $\text{P}$-beli $n$ ember valamelyike pingpongozik a harmadik társsal, legfeljebb $n\left(n-1\right)$. Ugyanez mondható az olyan hármasok számáról, amelyekben egy $\text{S}$-beli egyén sakkozik a harmadikkal és azokéról, amelyekben olyan $\text{T}$-beli szerepel, aki teniszezik a harmadikkal. A $3n^2$ számba vett hármas közül tehát legfeljebb $3n^2-3n$ az, amelyikre nem teljesül a feladat állítása; legalább $3n$ hármasra tehát teljesül.

 

Megjegyzések. 1. Ha a meggondolást a társaság mind a $3n+1$ tagjára megismételjük, akkor minden számba jövő hármast háromszor veszünk tekintetbe. Ennek alapján a társaságból kiválasztható összes olyan hármasok száma, amelyekben mind a három játékot játsszák egymás közt, legalább $n\left(3n+1\right)$. Ugyanazt a becslést nyertük, mint az első megoldásban. Szoros rokonságban is van a két megoldás, amennyiben az utóbbiban is olyan hármasok számának becslése útján jutottunk célhoz, amelyekben csak kétféle játékot játszanak.
A fenti megoldásban azokat a hármasokat vettük számba, amelyekben szerepel $A$, de a két társával ugyanazt a játékot játszó személy $\text{P}$-ben, $\text{S}$-ben, vagy $\text{T}$-ben van.

 

2. A nyert korlát $n=1$, $2$, $3$, $4$ esetén pontos. Ezt az első három esetben leolvashatjuk a 3. ábráról, amelyen a pontok a társaság tagjait képviselik, a folytonos vonallal összekötöttek a pingpongozó párokat jelölik, a szaggatott vonalak a sakkpartikat, a pontozott összekötések pedig a teniszezőket.

 

 

3.a ábra

 

 

 

3.b ábra

 

 

 

3.c ábra

 

Az $n=4$ esetben a $13$ embert körbe állítva mindenki a két szomszédjával és a harmadik szomszédjaival pingpongozik, a második és az ötödik szomszédjaival sakkozik, a negyedik és a hatodik szomszédjaival pedig teniszezik. Az ezt feltüntető ábrát bonyolultsága miatt jobb, ha az olvasó magának nagyban és esetleg színes vonalakkal rajzolja meg.
Nagyobb $n$-ekre már mindig nagyobb a megfelelő hármasok száma az itt nyert értéknél.^{${}^{*}$}

 

IV. megoldás. Eljárást adunk egy kívánt tulajdonságú hármas megkeresésére. Ismét a társaság előző megoldásokban szereplő csoportosításából indulunk ki. A $\text{P}$ csoport egy $P_1$ tagja sakkozik másik csoportbeli emberrel, mert $\text{P}$-ben rajta kívül $n-1$ ember van, tehát ennél több sakkpartnere sem lehet. Ha van sakkpartnere $\text{T}$-ben, akkor azzal és $A$-val a feladat követelményének megfelelő hármast alkotnak. Ha nincs, akkor egy $\text{S}$-beli $S_1$ sakkpartnerét véve, annak van teniszpartnere $\text{S}$-en kívül. Ha teniszezik $\text{P}$-beli társsal, akkor ismét megfelelő hármast alkotnak $A$-val. Ha nem, akkor egy $\text{T}$-beli $T_1$ teniszpartnerről ismét feltehetjük, hogy $\text{T}$-n kívüli pingpongpartnerei $\text{P}$-ben vannak. Egyet kiválasztva az eljárást folytathatjuk, míg el nem jutunk vagy egy olyan párhoz, akik $A$-val együtt megfelelő hármast alkotnak, vagy olyan valakihez, aki már korábban is szerepelt. Utóbbi esetben egy kört kapunk, amelyikben egy-egy $\text{P}$-, $\text{S}$-, $\text{T}$-beli személy követi egymást periodikusan, és mindenki olyan játékot játszik a rákövetkezővel, amilyent az utóbbi $A$-val játszik. Ha ez a kör három emberből áll, akkor ők megfelelő hármast alkotnak.
Megmutatjuk, hogy ha a kör ennél hosszabb, akkor kihagyható belőle három egymás utáni ember úgy, hogy a kör leírt szerkezete megmaradjon, vagy találunk egy megfelelő hármast. Legyen $S$, $T$, $P\text{'}$, $S\text{'}$, $T\text{'}$ a kör öt egymás utáni tagja. Ha $P\text{'}$ és $T\text{'}$ sakkozik, akkor $A$-val, ha pedig pingpongozik, akkor $S\text{'}$-vel alkotnak megfelelő hármast. Az az eset vizsgálandó tovább, ha teniszeznek. Ha $P\text{'}$ és $S$ teniszezik, akkor $A$-val, ha sakkoznak, akkor $T$-vel alkotnak megfelelő hármast; marad az az eset, ha pingpongoznak. Nézzük ekkor $S$-et és $T\text{'}$-t. Ha pingpongoznak, akkor $A$-val, ha sakkoznak, akkor a vizsgált esetben $P\text{'}$-vel alkotnak megfelelő hármast. Ha viszont $S$ és $T\text{'}$ teniszezik, akkor $T$, $P\text{'}$ és $S\text{'}$ kihagyása után is megmarad a kör föntebb leírt szerkezete. Így az eljárás véges számú ismétlésével eljutunk a feladat állításának megfelelő hármashoz.

 

Megjegyzések. 1. A társaság tagjait pontokkal, a köztük zajló különböző játékokat különböző fajta vonalakkal ábrázolva, ahogyan azt a 3. ábrán is tettük, gráf keletkezik. A vonalakat ‐ a gráf éleit ‐ megkülönböztethetjük különböző színek használatával. Az olyan gráfot, amelyikben minden pontot mindegyik másikkal összeköt egy él, teljes gráfnak nevezik. Gráfok nyelvén fogalmazva és csekély általánosítással a következő tételt nyerjük: Ha $m\geqq 3$ és egy $m$ szögpontú teljes gráf éleit $3$ színnel színezzük úgy, hogy az egy-egy szögpontból induló különböző színű élek száma legfeljebb eggyel különbözzék, akkor van a gráfban olyan $3$ pont, amelyeket különböző színű élek kötnek össze. A fenti megoldások az általánosabb esetben is célra vezetnek.

 

2. Láttuk, hogy az adott feltételek mellett nem csak létezik kívánt tulajdonságú hármas, de elég szép számban van. Kérdés, hogy nem lazíthatnánk-e a színeloszlás egyenletességének követelményén úgy, hogy a következmény még érvényes legyen. Nem elegendő-e például azt megkívánni, hogy bármelyik pontból induló egyszínű élek száma legalább az összes élek $\mathrm{0,3}$ része legyen?
Annyi biztos, hogy ez az arányszám nem vihető $1/4$ alá. Ez így látható be: vegyünk $4$, egyenként $n$ pontból álló ponthalmazt. Az egy halmazon belüli élek legyenek pirosak, azok, amelyek első és második halmazbeli pontokat vagy harmadik és negyedik halmazbelieket kötnek össze, kékek, a többi él legyen zöld. Ekkor minden pontból $n-1$ piros él indul ki, $n$ kék és $2n$ zöld, és könnyen látható, hogy nincs háromszínű háromszög. Felmerül a kérdés, hol van a kritikus határ $1/3$ és $1/4$ közt. Lapzártakor értesültünk, bizonyítást nyert, hogy az $1/4$ érték az.

---

^{${}^{*}$}Valójában $j+k\le n-1$ is fennáll, mert az illető egyik pingpongpartnere $A$.

^{${}^{*}$}Erre a kérdésre lapunkban visszatérünk (szerk.).