Kezdőlap


Cím:	Megjegyzések az 1987. évi Kürschák József matematikai tanulóverseny 3. feladatához
Szerző(k):	Surányi László
Füzet:	1988/november, 337 - 346. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi cikkben egy olyan gráfelméleti problémával foglalkozunk, amely szorosan kapcsolódik a címben említett feladathoz.^{$^{*}$} Úgy érezzük, mind a felmerülő kérdések, mind a megválaszolásukhoz használt módszerek jó betekintést nyújthatnak abba, hogyan jut el a gráfelmélet egy egyszerű feladat kis ,,megcsavarásával'', feltételeinek élesítésével a maga mély problémáihoz és azok megoldásához. A használt ötletek: egy adott tulajdonság szempontjából maximális v. minimális pont kiválasztása, egy adott tulajdonságra nézve ,,tömör'' rész keresése (Ramsey-típusú tételek), binomiális együtthatók összegének becslése, egyszerű szélsőérték-feladatok megoldása ,,többszörös leszámolással'' ‐ mind tipikus gráfelméleti ötletek. A cikk megértéséhez szinte alig kell valamit tudni, de aki nem látja át a szereplő kifejezések ,,nagyságrendjeit'' ( $n^{2}$ -es, vagy $n^{3}$ -ös-e pl. egy kifejezés), annak első olvasáskor célszerűbb ,,elhinnie'' a számolásokat, mint ,,elveszni'' a részletekben. Végül még egy tanács: aki most ismerkedik a gráfelmélet nehezebb kérdéseivel, annak ajánljuk, hogy először nézze át a II. tételt (ez jó példa a többszörös leszámolásra), az ott szereplő Ramsey-tétel bizonyítását, és próbálja magától bebizonyítani a (8) összefüggést^{$^{*}$}; ha pedig nem megy, nézze először át annak rövid bizonyítását. Ha ezt jól érti, a többi, hosszadalmasabb bizonyítással sem lesz gondja. ‐ Mindenekelőtt definiáljuk a fogalmakat, melyeket használni fogunk.
Cikkünkben a megoldás ismertetése után felvetett kérdésekkel foglalkozunk. Célszerű ehhez a gráfelmélet nyelvét használni. Először tehát röviden definiáljuk a fogalmakat. Egy $m$ pontú gráf teljes, ha bármely két pontját él köti össze. A gráfot $k$ -színűnek nevezzük, ha minden éléhez hozzá van rendelve $k$ szín valamelyike. (Tehát minden élnek pontosan egy színe van és összesen legfeljebb $k$ szín fordul elő.) A színeket általában egyszerűen sorszámmal jelöljük: $1$ . szín, $2$ . szín, stb. Egy $m$ pontú színezett teljes $G$ gráf minden ponthármasa három élű részgráfot (a továbbiakban röviden: hármast) határoz meg; ezek mindegyike egy-, kettő-, vagy háromszínű lehet. Az egyszínű hármasok számát $e_{G}$ -vel, a kétszínűekét $k_{G}$ -vel, a három-színűekét $h_{G}$ -vel jelöljük.
1.§ A feladatban olyan $3 n + 1$ pontú, háromszínű teljes gráf szerepel, amelyben minden pontból $n$ db $1$ ., $n$ db $2$ . és $n$ db $3$ . színű él indul. Az ilyen gráfot egyenletesen $3$ -színezett gráfnak nevezzük. A feladat azt állítja, hogy ilyen egyenletesen $3$ -színű gráfokban van háromszínű hármas, azaz $h_{G} > 0$ .
A feladat ismertetett megoldásai közül az I. és a III. megoldás ennél többet bizonyít, nevezetesen azt, hogy

\begin{matrix} h_{G} ≧ (3 n + 1) n . \end{matrix}

(1)

Felvethető a kérdés, vajon ,,jó becslés"-e ez

h_{G}

-re. Az összes hármasok száma ugyanis

\begin{matrix} (\binom{3 n + 1}{3}) = (3 n + 1) n \cdot \frac{3 n - 1}{2}, \end{matrix}

a kapott becslés tehát annyit mond, hogy a háromszínű hármasok száma az összes hármasnak legalább

\frac{2}{3 n - 1}

- edrésze. Ez az arány azonban az

n

növekedésével tetszőlegesen kicsi lehet,

{lim}_{n \to \infty}^{} \frac{2}{3 n - 1} = 0.

De valóban ilyen elenyésző-e a háromszínű hármasok száma az összes hármasokhoz képest? Cikkünk első részében megmutatjuk, hogy nem. Be fogjuk bizonyítani a következőt:

I. tétel. Létezik olyan

c

pozitív állandó, amelyre igaz, hogy egy

3 n + 1

pontú, egyenletesen háromszínű teljes gráfban

\begin{matrix} h_{G} > c \cdot (\binom{3 n + 1}{3}) . \end{matrix}

(2)

Első lépésben azt látjuk be, hogy

c

választható

1 / 340

-nek, vagyis az összes hármasnak majdnem a

3

ezreléke háromszínű. Később aztán megmutatjuk, hogy bármely

c < 1 / 36

szám is megfelel, tehát az összes hármasnak több mint

2,7 %

-a háromszínű. Másrészt megmutatható, hogy minden

n

-re van olyan egyenletes

3

-színezés, ahol csak

\frac{1}{6} (\binom{3 n + 1}{3})

háromszínű hármas van. Nyitott kérdés, hogy hol az igazság

1 / 36

és

\frac{1}{6}

között.
A tétel bizonyítása azon az észrevételen alapszik, hogy a közölt I. megoldás még (1)-nél is többet bizonyít. Nézzük végig tehát e megoldás gondolatmenetét.
Először is minden

m

-pontú

3

-színű teljes gráfban igaz a következő összefüggés:

\begin{matrix} h_{G} + k_{G} + e_{G} = (\binom{m}{3}) . \end{matrix}

(3)

Valóban: a jobb oldalon az összes hármasok száma áll, másrészt minden hármas egy-, kettő- vagy háromszínű, így e szám egyenlő

h_{G} + k_{G} + e_{G}

-vel.
Legyen most

G

egy

3 n + 1

pontú, egyenletesen

3

-színű teljes gráf, s legyen

x

egy tetszőleges pontja. Számoljuk meg, hogy

x

hány olyan

(x, y, z)

hármasban szerepel, ahol az

x y

és

x z

élek azonos színűek. Ez a szín háromféle lehet, és ha már rögzítettük, akkor

n

db olyan szomszédja van

x

-nek, amellyel a választott színű él köti össze. Ezekből kettőt

(\binom{n}{2})

-féleképp választhatunk ki, ami adott

x

-re összesen

3 (\binom{n}{2})

hármast jelent. Végül magát az

x

pontot

(3 n + 1)

-féleképpen választhatjuk ki. Összesen tehát

3 (3 n + 1) (\binom{n}{2})

hármast számoltunk össze. Eközben háromszínű hármasokat nem számoltunk, a kétszínűeket egyszer (az ,,egyszínű'' csúcspontjuknál), az egyszínűeket pedig mindegyik csúcspontjuknál, tehát háromszor is számbavettük.
Ezek szerint

\begin{matrix} k_{G} + 3 e_{G} = 3 (3 n + 1) (\binom{n}{2}) . \end{matrix}

(4)

Ha most (3)-ba beírjuk, hogy

m = 3 n + 1

, s kivonjuk belőle a (4) egyenletet, azt kapjuk, hogy

\begin{matrix} h_{G} = (3 n + 1) n + 2 e_{G} . \end{matrix}

(5)

Az I. tétel bizonyításához elég tehát belátnunk a következőt:

II. tétel. Ha

n ≧ 6

, akkor egy

3 n + 1

pontú, egyenletesen

3

-színű teljes gráfban

\begin{matrix} e_{G} ≧ \frac{1}{680} \cdot (\binom{3 n + 1}{3}) . \end{matrix}

Ebből ugyanis az I. tétel

c = 1 / 340

választással már következik, ha

n ≧ 6

. Másrészt

n = 1, 2, 3, 4, 5

-re

\begin{matrix} \frac{1}{340} \cdot (\binom{3 n + 1}{3}) ≦ \frac{1}{340} (\binom{16}{3}) < 4, \end{matrix}

holott (1)-ből

h_{G} ≧ 4

is következik. (Az I. tétel a

c = 1 / 340

állandóval csak

\frac{3 n - 1}{2} ≧ 340

, azaz

n ≧ 227

esetén ad jobb eredményt (1)-nél.)
Első pillanatban nem világos, miért lenne könnyebb a II. tételt bizonyítani, mint az I.-et. Miért lehetne könnyebben becsülni az egyszínű hármasok számát, mint a háromszínűekét? A válasz az, hogy általában, ha a színezésre nem kötünk ki semmit, akkor egy háromszínű

m

-pontú teljes gráfban nem feltétlenül van háromszínű hármas. (Ha pl. az egyik színt egyáltalán nem használjuk, biztos nincs, s a feladat ismertetése után^{$^{*}$} szerepelt olyan

m = 4 n

pontú teljes gráf, amelyben minden pontból minden színből legalább

n - 1 = \frac{1}{4} m - 1

él indul ki, s mégsincs benne háromszínű hármas (1. ábra).) Ezzel szemben egyszínű hármas minden ,,elég nagy'' ‐ legalább

17

pontú ‐ háromszínű teljes gráfban van.

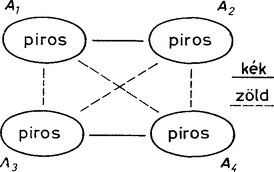1. ábra

Ez az alábbi, ún. Ramsey-típusú^{$^{*}$} tétel speciális esete:

n_{K} = [e \cdot K!] + 1 = K! (1 + \frac{1}{1!} + \frac{1}{2!} + ... + \frac{1}{K!}) + 1

, akkor egy

K

színű,

n_{K^{''}}

pontú teljes gráfban mindig van egyszínű hármas.
(A tétel bizonyítása megtalálható a Középiskolai Matematikai Versenyek 1977‐79. 261. oldalán.)

K = 3

-ra

n_{3} = 17

K = 2

-re

n_{2} = 6

, s a kapott állítás (minden hatpontú, kétszínű teljes gráfban van egyszínű háromszög) az 1947. évi Kürschák-verseny 2. feladata volt, más szöveggel.
A II. tétel bizonyítása innen már egyszerűen adódik. Ekkor ugyanis bármely

m ≧ 17

pontú háromszínű gráfban van egyszínű háromszög, méghozzá nem is kevés: minden

17

pontja tartalmaz legalább egyet. Ez összesen legalább

(\binom{m}{17})

egyszínű háromszög, így azonban mindegyiküket többször is megszámoltuk, nevezetesen

(\binom{m - 3}{14})

-szer, hiszen egy adott hármashoz a többi

m - 3

pontból ennyiféleképpen lehet még

14

pontot hozzávenni. Ez azt jelenti, hogy a gráfban legalább

\begin{matrix} \frac{(\binom{m}{17})}{(\binom{m - 3}{14})} = \frac{m!}{17! (m - 17)!} \cdot \frac{14! (m - 17)!}{(m - 3)!} = \frac{m (m - 1) (m - 2)}{17 \cdot 16 \cdot 15} = \\ = \frac{1}{(\binom{17}{3})} \cdot (\binom{m}{3}) = \frac{1}{680} (\binom{m}{3}) \end{matrix}

különböző egyszínű hármas van. Beláttuk tehát, hogy igaz a

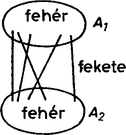
II'. tétel. Ha

m ≧ 17

, és

G

háromszínű,

m

-pontú teljes gráf, akkor

\begin{matrix} e_{g} ≧ \frac{1}{680} (\binom{m}{3}) . \end{matrix}

Ebből pedig a II. tétel

m = 3 n + 1

helyettesítéssel már következik és így az I. tétel bizonyítása is teljes. (Ha

n ≧ 6, m = 3 n + 1 ≧ 17

.) Természetes a kérdés, hogy mennyire pontos ez az

\frac{1}{680}

állandó. Az 1. ábrán látható gráfban kevesebb, mint

\frac{1}{16} \cdot (\binom{m}{3})

egyszínű háromszög van. A 2. ábra gráfján kevesebb, mint

\frac{1}{25} \cdot (\binom{m}{3})

egyszínű hármas van. Érdekes és nem teljesen tisztázott kérdés, hogy hol az igazság

\frac{1}{680}

és

\frac{1}{25}

között. (Az

\frac{1}{680}

-as szorzót később

\frac{1}{144}

-re fogjuk javítani.)

2. ábra

2.§ Bebizonyítottuk tehát az I. tételt

c = 1 / 340

állandóval. Felvetettük azt a kérdést is, hogy a II. tételhez hasonlóan nem lehet-e elhagyni az I. tételben is a színezés egyenletességére vonatkozó kikötést. Az 1. ábra gráfja mutatja, hogy ,,elég sok'' él kell minden színből. Erdős Pál vetette föl a következő kérdést:
Nevezzük egy

m

-pontú teljes gráf

3

-színezését

a

-egyenletesnek, ha minden pontjából legalább

a (m - 1)

1

. színű, s legalább ugyanennyi

2

. ill.

3

. színű él indul ki. (Nyilván csak

a ≦ \frac{1}{3}

esetén képzelhető el ilyen színezés, hiszen az egy pontból induló élek száma

m - 1

, s ez nem lehet kevesebb

3 a (m - 1)

-nél. Ha

a = \frac{1}{3}

, akkor

m = 3 n + 1

alakú, s a színezés egyenletes.) Kérdés:

a

milyen értékeire igaz, hogy minden

a

-egyenletesen háromszínű,

m

-pontú teljes gráfban van háromszínű hármas?^{$^{*}$}
Az első ötletünk az, hogy keressük meg (5) megfelelőjét

a

-egyenletes színezésekre, hiszen ennek segítségével vezettük vissza a háromszínű hármasok számának kérdését az egyszínűekére. Evégett még egyszer áttekintjük az (5)-öt bizonyító gondolatmenetünket.
Legyen

G

egy háromszínű,

m

-pontú teljes gráf, s legyen

x

egy tetszőleges pontja. Jelölje rendre

d_{1} (x), d_{2} (x)

és

d_{3} (x)

x

-ből induló

1

2.

és

3

. színű élek számát. Ekkor nyilván

\begin{matrix} d_{1} (x) + d_{2} (x) + d_{3} (x) = m - 1. \end{matrix}

(6)

Az egyenletes színezésnél

m = 3 n + 1

és

d_{1} (x) = d_{2} (x) = d_{3} (x) = n

volt. Megszámoltuk, hogy az

x

hány olyan

(x, y, z)

hármasban van benne, ahol

x y

és

x z

színe azonos. Ezt most is megtehetjük: az

x y

és

x z

él színe pontosan akkor lesz az

i

. szín, ha

y

-t és

z

-t az

x

-nek azon

d_{i} (x)

szomszédja közül választjuk, amellyel

i

. színű él köti össze. Ilyen

(y, z)

pár tehát

(\binom{d_{i} (x)}{2}) = \frac{d_{i}^{2} (x) - d_{i} (x)}{2}

van. Az

x

pont tehát

\begin{matrix} (\binom{d_{1} (x)}{2}) + (\binom{d_{2} (x)}{2}) + (\binom{d_{3} (x)}{2}) = \frac{1}{2} (d_{1}^{2} (x) + d_{2}^{2} (x) + d_{3}^{2} (x)) - \frac{m - 1}{2} \end{matrix}

olyan hármasban van benne, ahol

x y

és

x z

színe azonos. (Az egyenletes színezésnél ez a szám

3 (\binom{n}{2})

.) Ha most összeadjuk a

G

gráf minden

x

csúcsára így kiszámolt értékeket, akkor a kétszínű hármasokat pontosan egyszer, az egyszínűeket pedig háromszor számoljuk (a háromszínűeket egyszer sem). Így a következő összefüggést kapjuk:

\begin{matrix} k_{G} + 3 e_{G} = \frac{1}{2} \sum_{x \in G}^{} (d_{1}^{2} (x) + d_{2}^{2} (x) + d_{3}^{2} (x) - \frac{m - 1}{2}) . \end{matrix}

(4')

Ez a képlet (4) megfelelője tetszőleges háromszínű teljes

G

gráfnál. (Az összegzés a

G

pontjaira történik.) Ha ezt (3)-ból kivonjuk, megkapjuk (5) megfelelőjét:

\begin{matrix} h_{G} = 2 e_{G} + (\binom{m}{3}) - \frac{1}{2} \sum_{x \in G}^{} (d_{1}^{2} (x) + d_{2}^{2} (x) + d_{3}^{2} (x) - (m - 1)) . \end{matrix}

(5')

A talált eredmény egyelőre nem túl áttekinthető. De ha meggondoljuk, hogy mi a célunk vele, rögtön könnyebben kezelhető lesz. A háromszínű hármasok

h_{G}

számát akarjuk ‐ rögzített

m

mellett ‐ az egyszínűek

e_{G}

számával alulról becsülni, éspedig

a

-egyenletes színezések esetén. Ehhez viszont elég a

d_{1}^{2} (x) + d_{2}^{2} (x) + d_{3}^{2} (x)

összeget felülről becsülni.

d_{i} (x)

számokra több kikötésünk is van: összegük (6) szerint

m - 1

, és

d_{i} (x) ≧ a (m - 1)

, mert a színezés

a

-egyenletes. Bevezetve az

a_{i} = \frac{d_{i} (x)}{m - 1}

jelölést:

\begin{matrix} a_{1} + a_{2} + a_{3} = 1, a_{1} ≧ a, a_{2} ≧ a, a_{3} ≧ a, \end{matrix}

(7)

s e feltételek mellett keressük

\begin{matrix} d_{1}^{2} (x) + d_{2}^{2} (x) + d_{3}^{2} (x) = (a_{1}^{2} + a_{2}^{2} + a_{3}^{2}) {(m - 1)}^{2}, \end{matrix}

tehát

a_{1}^{2} + a_{2}^{2} + a_{3}^{2}

maximumát. Az

x^{2}

függvény konvexitásából könnyen biztosítható az alábbi

Lemma: A (7) feltételek mellett

a_{1}^{2} + a_{2}^{2} + a_{3}^{2}

akkor és csak akkor maximális, ha két

a_{i}

értéke

a

, a harmadiké

1 - 2 a

. Ez esetben az összeg értéke

2 a^{2} + {(1 - 2 a)}^{2} = 6 a^{2} - 4 a + 1

. (ld. a F. 2686. feladatot e szám 371. oldalán.)
Térjünk most vissza (5') képletünkhöz! A jobb oldalon szereplő összeg minden tagjáról tudjuk most már, hogy legföljebb

\begin{matrix} (6 a^{2} - 4 a + 1) {(m - 1)}^{2} - (m - 1) = (6 a^{2} - 4 a + 1) (m - 1) (m - 2) - (4 a - 6 a^{2}) (m - 1) < \\ < (6 a^{2} - 4 a + 1) (m - 1) (m - 2), \end{matrix}

mert

0 < a ≦ \frac{1}{3}

esetén

4 a - 6 a^{2} > 0

. így (5') jobb oldalán az

m

tagú összeg minden tagja legföljebb ennyi, tehát azt kapjuk, hogy

\begin{matrix} h_{G} > 2 e_{G} - \frac{1}{2} m (m - 1) (m - 2) (6 a^{2} - 4 a + 1) + (\binom{m}{3}) = \\ = 2 e_{G} - (\binom{m}{3}) (3 (6 a^{2} - 4 a + 1) - 1) = 2 (e_{G} - {(1 - 3 a)}^{2} (\binom{m}{3})) . \end{matrix}

Vagyis tetszőleges

m

-pontú,

a

-egyenletesen háromszínű teljes

G

gráfban igaz, hogy

\begin{matrix} h_{G} > 2 (e_{G} - {(1 - 3 a)}^{2} (\binom{m}{3})) . \end{matrix}

(5'')

Sikerült tehát az

a

-egyenletes színezésre az (5)-höz hasonló, egyszerű becslést kapnunk a háromszínű hármasok számára.
A becslés természetesen annál ,,rosszabb'', minél kevésbé egyenletes a színezés, tehát minél kisebb az

a

. (Ne felejtsük, hogy

a > \frac{1}{3}

nem lehetséges!) Az

a = \frac{1}{3}

esetre még

h_{G} > 2 e_{G}

adódik belőle, ami nem lényegesen rosszabb (5)-nél. Ez azt mutatja, hogy a becslés ,,elég pontos'', legalábbis

a = \frac{1}{3}

közelében. (Valójában minden

a

-ra elég erős a becslésünk.)
Nézzük, mire használható. A II' tétel szerint tetszőleges háromszínezésre

e_{G} ≧ \frac{1}{680} (\binom{m}{3})

(ha

m ≧ 17

). Ebből viszont következik, hogy ha

{(1 - 3 a)}^{2} < \frac{1}{680}

, tehát ha

\frac{1}{3} - \frac{1}{3 \sqrt[]{680}} < a ≦ \frac{1}{3}

, akkor (5'') jobb oldalán pozitív (

m

-től független) szám áll a zárójelben. Tehát

\frac{1}{3} ≧ a > \frac{1}{3} - \frac{1}{3 \sqrt[]{680}} \sim 0,32 055

esetén nemcsak hogy van háromszínű hármas, hanem az összes hármasok ,,pozitív százaléka'' háromszínű:

III. tétel. Ha

\frac{1}{3} ≧ a > \frac{1}{3} - \frac{1}{3 \sqrt[]{680}}

és

m ≧ 17

, akkor minden

m

-pontú,

a

-egyenletesen háromszínű teljes gráfban van háromszínű hármas. A háromszínű és az összes hármasok aránya egy rögzített (

m

-től független) pozitív szám,

\frac{1}{680} - {(1 - 3 a)}^{2}

fölött van.
3.§ Most szeretnénk csökkenteni az

a

-ra kapott

(\frac{1}{3} - \frac{1}{3 \sqrt[]{680}})

alsó korlátot. (5'') szerint ehhez

e_{G}

-re kellene az

\frac{1}{680} (\binom{m}{3})

-nál jobb alsó becslést találnunk. Ha meggondoljuk, erre is van kilátásunk, hiszen ezt az alsó becslést tetszőleges színezésre kaptuk, de most elég volna az

a

-egyenletes színezések esetén javítani rajta.
A következő észrevételből indulunk ki: ha

x

egy

a

-egyenletesen színezett teljes gráf egy pontja, akkor ,,elég sok''

1

. színű él indul belőle, ezek végpontjai tehát önmagukban is nagy ‐ legalább

a (m - 1)

pontú ‐ teljes részgráfot alkotnak. Ha e teljes részgráf minden éle

1

. színű, akkor máris van

(\binom{a (m - 1)}{3}) \sim a^{3} (\binom{m}{3}) 1

. színű háromszögünk. Ha viszont egyáltalán nincs benne

1

. színű él, akkor egy kétszínű nagy teljes részgráfunk van, amelyben várhatóan megint sok lesz az egyszínű háromszög. Általában e két szélsőséges eset valamilyen keverékét kell megpróbálnunk jellemezni. Ezt a következőképp tesszük: legyen

D_{i}

azon pontok halmaza, amelyeket

i

-színű él köt össze

x

-szel. (

D_{i}

-nek ekkor

D_{i} (x)

pontja van.) A

D_{i}

pontjai között futó

i

-színű élek számát jelölje

e_{i}

. Ekkor az

x

pontosan

e_{i}

darab

i

-színű, egyszínű hármasban van benne. Tekintsük most a

D_{i}

pontjai által alkotott részgráfot, s változtassuk meg ebben az

e_{i}

i

-színű él színét a másik két szín egyikére. Az így kapott

d_{i} (x)

pontú teljes gráf már csak kétszínű.
Szükség volna tehát egy kétszínű teljes gráf egyszínű hármasai számának alsó becslésére, majd meg kell gondolnunk, hogy az ilyen egyszínű hármasoknak csak egy része jöhetett létre a színezés megváltoztatásával. Próbálkozhatnánk a II' tétel bizonyításakor követett módszerrel (Ramsey-típusú tételre való hivatkozás), de ez most igen durva eredményhez vezet. Vegyük észre, hogy (5') most is használható, és pontosabb becslést ad. Egy kétszínű, teljes gráf ugyanis olyan háromszínű teljes gráfnak is tekinthető, amelyben a

3

. szín nem szerepel, tehát minden

x

pontra

d_{3} (x) = 0

. Ekkor persze háromszínű hármas egyáltalán nincsen,

h_{G} = 0

. Így (5') alapján pontos értéket nyerünk az egyszínű hármasok számára:

\begin{matrix} 4 e_{G} = \sum_{x \in G}^{} (d_{1}^{2} (x) + d_{2}^{2} (x) - (m - 1)) - 2 (\binom{m}{3}) . \end{matrix}

Az összegzés

G

minden pontjára történik.

d_{1} (x) + d_{2} (x) = m - 1

, így a négyzetes és számtani közép közötti összefüggés alapján

d_{1}^{2} (x) + d_{2}^{2} (x) ≧ \frac{{(m - 1)}^{2}}{2}

. A jobb oldalon az összegnek

m

tagja van, így az legalább

\begin{matrix} m (\frac{{(m - 1)}^{2}}{2} - (m - 1)) = \frac{m (m - 1) (m - 3)}{2} = 3 \cdot (\binom{m}{3}) \cdot \frac{m - 3}{m - 2} . \end{matrix}

Az egész jobb oldal így legalább

(\binom{m}{3}) (1 - \frac{3}{m - 2})

, tehát egy kétszínű,

m

-pontú teljes gráfban

\begin{matrix} e_{G} ≧ \frac{1}{4} (\binom{m}{3}) (1 - \frac{3}{m - 2}) = \frac{1}{4} (\binom{m}{3}) - \frac{1}{4} (\binom{m}{2}) = \frac{1}{4} (\binom{m - 1}{3}) - \frac{1}{4} (m - 1) . \end{matrix}

(8)

Az összes hármasoknak tehát majdnem az

1 / 4

-e egyszínű. (Ez a becslés nagyjából pontos:

m = 2 n

esetén a 3. ábrán látható kétszínű,

m

-pontú gráfban

\frac{1}{4} (\binom{m}{3}) (1 - \frac{3}{m - 1})

egyszínű hármas van.)

3. ábra

Térjünk most vissza a

D_{i}

. részgráfunkhoz, amelyben

e_{i}

db él színezését megváltoztattuk, hogy kétszínű legyen. (8) szerint most legalább

\frac{1}{4} (\binom{d_{i} - 1}{3}) - \frac{1}{4} (d_{i} - 1)

egyszínű hármas van benne. (

d_{i} (x)

helyett mostantól röviden

d_{i}

-t írunk, ez nem fog félreértésre okot adni.)
Ha most az

e_{i}

db átfestett élnek visszaadjuk eredeti színét, akkor ezzel legföljebb

e_{i} (d_{i} - 2)

hármas színezését változtatjuk meg, hiszen

D_{i}

-ben egy él összesen

d_{i} - 2

hármasban van benne. Így legföljebb

e_{i} (d_{i} - 2)

egyszínű hármas színezése romlik el, tehát

D_{i}

-ben még mindig marad legalább

\begin{matrix} \frac{1}{4} (\binom{d_{i} - 1}{3}) - \frac{1}{4} (d_{i} - 1) - e_{i} d_{i} + 2 e_{i} \end{matrix}

egyszínű hármas. (Ez akkor is igaz, ha az így kapott szám negatív volna.) Ha ezt

D_{1}

-re,

D_{2}

-re,

D_{3}

-ra végigcsináljuk, a gráf egyszínű hármasainak számára az

\begin{matrix} e_{G} > \frac{1}{4} ((\binom{d_{1} - 1}{3}) + (\binom{d_{2} - 1}{3}) + (\binom{d_{3} - 1}{3}) - (m - 4)) - (e_{1} d_{1} + e_{2} d_{2} + e_{3} d_{3}) \end{matrix}

(9)

becslést kapjuk. (A

2 (e_{1} + e_{2} + e_{3})

tagról nyugodtan elfelejtkezhetünk, az a kivonandó mellett ,,nem rúg labdába''.)

A kapott becslés most sem túl áttekinthető. De az

(\binom{x}{3}) = \frac{{(x - 1)}^{3} - (x - 1)}{6}

képlet alapján a harmadik hatványközép és a számtani közép közötti egyenlőtlenség segítségével a jobb oldali binomiális együtthatók összege becsülhető alulról:

\begin{matrix} (\binom{d_{1} - 1}{3}) + (\binom{d_{2} - 1}{3}) + (\binom{d_{3} - 1}{3}) = \frac{1}{2} \frac{{(d_{1} - 2)}^{3} + {(d_{2} - 2)}^{3} + {(d_{3} - 2)}^{3}}{3} - \frac{m - 7}{6} ≧ \\ ≧ \frac{1}{2} {(\frac{m - 7}{3})}^{3} - \frac{m - 7}{6} . \end{matrix}

Mármost ellenőrizhető, hogy ha

m ≧ 3

, akkor a kapott egyenlőtlenség jobb oldalára

\begin{matrix} \frac{1}{2} {(\frac{m - 7}{3})}^{3} - \frac{m - 7}{6} > \frac{1}{9} (\binom{m}{3}) (1 - \frac{18}{m - 2}) + (m - 4), és így \\ (\binom{d_{1} - 1}{3}) + (\binom{d_{2} - 1}{3}) + (\binom{d_{3} - 1}{3}) - (m - 4) > \frac{1}{9} (\binom{m}{3}) (1 - \frac{18}{m - 2}) . & (10) \end{matrix}

Még a (9)-ben szereplő

e_{1} d_{1} + e_{2} d_{2} + e_{3} d_{3}

-ra kell találnunk egy felső becslést. Vegyük észre, hogy eddig nem használtuk ki a színezés

a

-egyenletességét (egyébként ezért is nem adja gondolatmenetünk a lehető legjobb eredményt). Most viszont kihasználjuk, méghozzá abban a formában, hogy

i = 1, 2, 3

-ra

d_{i} ≦ (1 - 2 a) (m - 1)

, ami

d_{i} ≧ a (m - 1)

és

d_{1} + d_{2} + d_{3} = m - 1

-ből következik. Ezért

\begin{matrix} e_{1} d_{1} + e_{2} d_{2} + e_{3} d_{3} ≦ (e_{1} + e_{2} + e_{3}) (1 - 2 a) (m - 1) . \end{matrix}

(11)

Most

(e_{1} + e_{2} + e_{3})

-at kell még felülről becsülnünk. Mint láttuk,

e_{1} + e_{2} + e_{3}

éppen az olyan egyszínű hármasok száma, amelyek tartalmazzák

x

-et. Összesen

e_{G}

db egyszínű hármas van, és minden hármasban három pont, egy pont tehát átlagosan

\frac{3 e_{G}}{m}

egyszínű hármasban van benne. S miután

x

-ről eddig nem tettünk fel semmit, most feltehetjük, hogy (az egyik) olyan pont, amelyik minimális számú egyszínű hármasban fordul elő. Ez a minimum legföljebb

\frac{3 e_{G}}{m}

és

\begin{matrix} e_{1} + e_{2} + e_{3} ≦ \frac{3 e_{G}}{m} . \end{matrix}

Ezt (11)-gyel összevetve

\begin{matrix} e_{1} d_{1} + e_{2} d_{2} + e_{3} d_{3} ≦ 3 e_{G} (1 - 2 a) \frac{m - 1}{m} < 3 e_{G} (1 - 2 a) . \end{matrix}

Ezt, valamint (10)-et (9)-be beírva :

\begin{matrix} e_{G} > \frac{1}{36} (\binom{m}{3}) (1 - \frac{18}{m - 2}) - (3 - 6 a) e_{G}, \end{matrix}

ahonnan azt kapjuk, hogy egy

a

-egyenletesen háromszínű,

m

pontú teljes

G

gráfban

\begin{matrix} e_{G} > \frac{1}{36 (4 - 6 a)} (\binom{m}{3}) (1 - \frac{18}{m - 2}) . \end{matrix}

(12)

(Ha

a = 0

, akkor a színezésre nincs kikötés. Ez esetben a II' tétel élesítését kapjuk: egy

m

-pontú, háromszínű teljes gráfban az összes hármasnak legalább

\frac{1}{144} (1 - \frac{18}{m - 2})

-d része egyszínű. Nagy

m

-ekre az

1 - \frac{18}{m - 2}

szorzó egyre közelebb van az

1

-hez, így az összes hármasnak majdnem az

\frac{1}{144}

-edrésze egyszínű. Ez azonban még mindig messze van a legjobb eredménytől.)
Most már nincs más dolgunk, mint összevetni (12)-t (5'')-vel:

IV. tétel. Ha

G

m

-pontú,

a

-egyenletesen háromszínű teljes gráf, akkor

\begin{matrix} e_{G} > \frac{1}{36 (4 - 6 a)} (\binom{m}{3}) (1 - \frac{18}{m - 2}), és így \\ h_{G} > 2 (\frac{1}{36 (4 - 6 a)} (1 - \frac{18}{m - 2}) - {(1 - 3 a)}^{2}) (\binom{m}{3}) . \end{matrix}

Ha tehát

\frac{1}{36 (4 - 6 a)} > {(1 - 3 a)}^{2}

, akkor ‐ legalábbis elég nagy

m

-ekre ‐ a zárójelben pozitív szám áll, s így igaz az alábbi

Következmény: Ha

1 > (4 - 6 a) {(1 - 3 a)}^{2} \cdot 36

, ha tehát pl.

a > 0,2961

, akkor minden elég nagy

m

-re az

m

-pontú teljes gráf bármely

a

-egyenletes háromszínezésében van háromszínű hármas, sőt az ilyenek és az összes hármasok számának az aránya egy csak az

a

-tól függő szám fölött marad.
Valóban: ha

b = \frac{1}{36 (4 - 6 a)} - {(1 - 3 a)}^{2} > 0

, akkor elég nagy

m

-re

\frac{1}{36 (4 - 6 a)} \times \frac{18}{m - 2} < \frac{b}{2}

, s így elég nagy

m

-re

h_{G} > b (\binom{m}{3})

.
Megjegyezzük még, hogy (9)-ben a kisebbítendőt a

d_{1} = d_{2} = d_{3} = \frac{1}{3} (m - 1)

értékkel becsültük, míg a kivonandót a

d_{1} = d_{2} = a (m - 1), d_{3} (1 - 2 a) (m - 1)

értékkel. Ha kicsit óvatosabban járnánk el, és a kisebbítendőt és kivonandót hasonlóan becsülnénk, valamivel jobb becsléseket kapnánk.

^{$^{*}$} A feladatot lásd a KÖMAL 1988/2 számának 56‐57. oldalán.

^{$^{*}$}Vagyis azt, hogy ha egy $n$ pontú teljes gráf minden élét fehérre vagy feketére színezzük, a hármasoknak ,,durván'' legalább a negyede egyszínű lesz.

^{$^{*}$}Lásd a KÖMAL 1988/2 számának 57. oldalán a 2. megjegyzést.

^{$^{*}$}A Ramsey-típusú tételek olyan állítások, amelyek azt mondják ki, hogy egy ,,elég nagy'' $K$ -színű gráfban van egy előre megadott típusú egyszínű részgráf (a mi esetünkben háromszög).

^{$^{*}$} Kostoczka, lengyel matematikus a közelmúltban megmutatta, hogy a $a ≧ \frac{1}{4}$ esetén mindig létezik $3$ -színű hármas, egyébként nem feltétlenül.