Cím: Egy Kürschák-feladat általánosítása
Szerző(k):  Kós Géza 
Füzet: 1988/április, 145 - 153. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bevezetés

 

Az 1986. évi Kürschák-versenyen szerepelt az alábbi feladat:
 

A és B a következő játékot játssza: Az első 100 pozitív egész közül véletlenszerűen kiválasztanak k darabot és ha ezek összege páros, akkor A, egyébként pedig B nyer. A k milyen értékeire lesz egyenlő A és B nyerési esélye?
 

A válasz: páratlan k esetén a nyerési esélyek egyenlők, páros k esetén pedig nem: ha k/2 páros, akkor A, ha pedig k/2 páratlan, akkor B nyerési esélye nagyobb.
A KÖMAL 1987/2 számában közölt I. megoldás akkor is alkalmazható, ha valamilyen páros n-re A és B nem az első 100, hanem az első n pozitív egész közül választ ki k darabot (érdemes meggondolni, mit ad a módszer páratlan n-re).
Természetesnek tűnt a következő általánosítás: mit mondhatunk akkor, ha nem kettő, hanem m játékos játszik, úgy, hogy az m valamilyen n többszörösére az első n pozitív egész közül véletlenszerűen kiválasztanak k darabot, ezek összegét maradékosan elosztják m-mel, és a maradék határozza meg a nyertes személyét: 0 maradék esetén az első, 1 maradék esetén a második és általában, r maradék esetén az (r+1)-edik játékos nyer?
 

Egy speciális eset
 

Viszonylag könnyű volt megtalálnom a választ akkor, ha az m prímszám: ebben az esetben a játék pontosan akkor igazságos, ha a k nem osztható m-mel, azaz (k,m)=1.
Osszuk be ugyanis az első n pozitív egészt n/m darab m elemű ,,blokkba'': (1,2,...,m),(m+1,...,2m),...,(n-m+1,...,n), és tekintsük azokat a k-asokat, amelyek mindegyikéhez található olyan blokk, amelynek a k-as tartalmazza legalább egy, de nem az összes elemét. Az ilyen k-asokat m elemű osztályokra fogjuk bontani úgy, hogy egy-egy osztályban a k-asok elemeinek összegei minden lehetséges maradékot kiadnak m-mel osztva.
Úgy kapjuk meg egy k-ashoz a vele egy osztályban levő további (m-1) darabot, hogy megkeresve a legelső olyan blokkot, amelynek legalább egy, de nem az összes elemét kiválasztottuk, az adott k-asnak az ebbe a blokkba eső elemeit minden lehetséges módon ,,elforgatjuk'': azaz mindegyiküket növeljük ugyanazzal a 0 és m-1 közé eső egésszel, majd azokat az elemeket, amelyek ezáltal kikerülnek a blokkból, m-mel csökkentjük, hogy visszakerüljenek. Tegyük fel, hogy a kiinduló k-as a blokkból d darab elemet tartalmaz (1≤d<m) és e k-asban az elemek összege S. Ekkor a k-ast tartalmazó osztályban a k-asok összegei m-mel osztva az S,S+d,S+2d,...S+(m-1)d számokkal egyenlő maradékokat adnak, hiszen ha a d darab blokkbeli elem mindegyikéhez i-t adunk (0≤i<m), majd néhányat m-mel csökkentünk, egy S+id-vel kongruens számot kapunk (modm). Ez az m darab szám pedig csupa különböző maradékot ad m-mel osztva, mert ha S+id≡S+jd(modm), akkor m osztója (i-j)d-nek, ami -m<i-j<m és 1≤d<m miatt csak úgy lehetséges, ha i-j=0, azaz i=j, hiszen az m prím. Mivel pedig a lehetséges maradékok száma éppen m, valóban előáll az összes lehetséges maradék. Az eddig vizsgált (nem üres ‐ nem teli blokkokat tartalmazó) k-asokon játszva tehát igazságos a játék.
A fennmaradó k-asok azok, amelyek minden blokknak vagy mind az m elemét tartalmazzák, vagy egyet sem; ilyenek csak akkor vannak, ha m, a blokk mérete osztója a k-as elemszámának, azaz k-nak. Az ilyen k-asokban az elemeket m-mel osztva minden lehetséges maradékot egyaránt k/m esetben kapunk, így az elemek összege kongruens
(0+1+2+...+(m-1))⋅k/m=k(m-1)2-vel(modm).

Ez viszont azt jelenti, hogy az ilyen k-asok összegei m-mel osztva ugyanazt a maradékot adják, az m darab játékos közül tehát egynek nagyobb a nyerési esélye a játékban, annak, aki a fenti maradéknál nyer.
Ha tehát m nem osztója a k-nak, akkor a játék igazságos, egyébként pedig nem.
A bizonyítás m=2 esetén megegyezik az eredeti feladat megoldásával.
Most már könnyű volt megadni a játék igazságosságának egy szükséges feltételét az általános esetre: az m-nek és a k-nak relatív prímnek kell lennie. Tegyük fel ugyanis, hogy a játék igazságos, de m-nek és k-nak mégis van egy közös p prímosztója. Osszuk be a játékosokat p csapatba úgy, hogy az i-edik csapatba az i-edik, a (p+i)-edik, (2p+i)-edik, ...,(m-p+i)-edik játékos kerüljön (i=1,2,...,p). Ekkor minden csapatban m/p játékos lesz.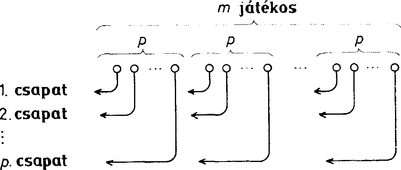
 
 
1. ábra
 

Játsszák most a játékot úgy, hogy ne egy játékos nyerjen, hanem az a csapat, amelyiknek tagja az illető játékos. Mivel feltevésünk szerint az ,,egyéni'' játék igazságos és minden csapat ugyanannyi játékosból áll, a játék a csapatok között is igazságos.
Ugyanakkor azt, hogy melyik csapat nyer, az dönti el, hogy milyen maradékot ad a kiválasztott k darab szám összege p-vel osztva: a i-edik csapat ugyanis akkor nyer, ha az összeg m-mel osztva i-1,p+i-1,...,m-2p+i-1,m-p+i-1, azaz p-vel osztva i-1 maradékot ad. Láttuk viszont, hogy az ilyen játék nem lehet igazságos ‐ mert k osztható p-vel ‐, és így az eredeti egyéni játék sem az.
Azt sem volt nehéz bebizonyítani, hogy a kapott szükséges feltétel elégséges is: ha k és m relatív prímek, akkor a játék igazságos: az m=prím esetben talált ,,forgatásos'' bizonyítás ugyanis most is működik, ennek végiggondolását az Olvasóra hagyjuk.
 

Hogyan tovább?
 

Ezután természetesen azzal kezdtem foglalkozni, mit mondhatunk akkor, ha nem kötjük ki, hogy m, a játékosok száma, osztója legyen n-nek. '87 februárjában sikerült bebizonyítanom a következőket:
‐ ha m prímszám, akkor a játék igazságosságának szükséges és elégséges feltétele,
 hogy k adjon m-mel osztva nagyobb maradékot, mint n ad m-mel osztva;
 (a már vizsgált m∣n esetben ez a talált m∤k feltételt jelenti)
‐ ha m=pα, ahol p prímszám és α pozitív egész, akkor a feltétel az, hogy
 minden 1≤i≤α-ra k adjon pi-nel osztva nagyobb maradékot,mint n ad pi
 -nel osztva.
 

Ezekből az általános esetre is kaptam egy szükséges feltételt: ha a játék igazságos, akkor minden olyan p prímszámra és i pozitív egészre, amelyre pi osztója m-nek, k nagyobb maradékot kell, hogy adjon pi-nel osztva, mint n (a bizonyítást a csapatba rendezéses módszerrel gondolja meg az Olvasó).
A továbbiakban jelöljük egy a szám b-vel való osztásakor kapott maradékát a(modb)-vel.
A fenti feltétel nem elégséges: például ha m=10,n=6 és k=3, akkor teljesül, hiszen 3(mod2)=1>6(mod2)=0 és 3(mod5)=3>6(mod5)=1, a játék viszont nem igazságos: az első 6 pozitív egészből kiválasztható számhármasok összegét 10-zel elosztva rendre 3,3,3,2,1,1,1,1,2,3 esetben kapunk 0,1,...,9 maradékot.
 

A valódi feltétel és az elégségesség bizonyítása
 

A prímhatvány m-ekre kapott feltétel lényegibb általánosításának látszott, ha a maradékok nagyságviszonyára vonatkozó előírást nem csak az m prímhatvány osztóira kötjük ki, hanem az összes 1-nél nagyobb osztóra:
,,Az m minden 1-nél nagyobb d osztójára adjon a k nagyobb maradékot d-vel osztva, mint az n, azaz legyen k(modd)>n(modd).''
A vizsgált példán ez a d=m=10 esetre nem teljesül, hiszen 3(mod10)==3<6(mod10)=6.
Sikerült bebizonyítanom, hogy ez a feltétel elegendő, de azt akkor még nem, hogy valóban szükséges. A szükségességet csupán arra az esetre tudtam visszavezetni, ha n<m; elég lett volna igazolni, hogy ha ilyenkor nem teljesül, akkor a játék nem igazságos. Ez csak több, mint fél év múlva sikerült.
Nyáron megbeszéltem Reiman tanár úrral, hogy előadom az addigi eredményeket az Ifjúsági Matematikai Körben. Szerencsére sikerült megtalálnom a hiányzó bizonyítást ‐ két nappal (!) az előadás előtt. Ehhez a komplex számokat használtam fel, és később ezek segítségével új bizonyítást találtam arra, hogy a feltétel szükséges és elégséges. Ezeket a cikknek egy későbbi számban megjelenő második részében írom le.
És most következzék a feltétel elégségességének bizonyítása!
 

A továbbiakban azt a játékot, melynek során m játékos az első n pozitív egész közül véletlenszerűen kiválaszt k darabot (k≤n), ezek összegét maradékosan elosztják m-mel, és a maradék dönti el a nyertes személyét, J(m,n,k)-val fogom jelölni. (Az eredeti Kürschák-feladatbeli játék eszerint J(2,100,k).)
Megengedjük az olyan elfajuló játékokat is, amikor m=1, vagy k=0, esetleg n=k=0. Az m=1 esetben a játékot igazságosnak tekintjük.
 

ÁLLÍTÁS:    A J(m,n,k) játék igazságos, ha teljesül a következő
 

FELTÉTEL: Ha d az m-nek egy 1-nél nagyobb osztója, akkor k nagyobb
  maradékot ad d-vel osztva, mint n, azaz k(modd)>n(modd).
 

A bizonyítást m ‐ a játékosok száma ‐ szerinti teljes indukcióval végezzük. Ha m=1, akkor a játék igazságos, a feltétel pedig ekkor semmitmondó: mindig teljesül, mert az m-nek nincs 1-nél nagyobb osztója.
Legyen az m egy 1-nél nagyobb egész szám és tegyük fel, hogy az állítást már igazoltuk minden olyan J(m',n',k') játékra, amikor m'<m. Most bebizonyítjuk, hogy ha a Feltétel teljesül a J(m,n,k) játékra, akkor az igazságos.
Most is osszuk be az első n pozitív egészt [n/m] darab m elemű és egy darab n-m⋅[n/m]=n0 elemű blokkra:
{1,2,...,m},{m+1,...,2m},...,{[n/m]m-m+1,...,[n/m]m},{[n/m]m+1,[n/m]m+2,...,n}



Az m elemű blokkokat ,,teljes'', az utolsó, n0 eleműt pedig ,,csonka'' blokknak nevezzük. Ha m osztója az n-nek, akkor a csonka blokk természetesen üres. A teljes blokkokat megszámozzuk: az i-edik teljes blokk az im-m+1,im-m+2,...,im számokból áll.
Tekintsünk egy tetszőleges k-ast. Azt állítjuk, hogy ha a Feltétel teljesül, akkor található hozzá olyan teljes blokk, amellyel valódi metszete van, tehát nem üres és nem is az egész blokk.
Ha nincs ilyen blokk, akkor a kiszemelt k-as minden teljes blokkból 0 vagy m elemet tartalmaz és így
k(modm)≤n0=(modm).
Ezt viszont a Feltétel kizárja (d=m).
 

Most is osztályokba rendezzük a k-asokat, mégpedig úgy, hogy egy adott k-as ‐ hívjuk mintának ‐ azokkal a k-asokkal legyen egy osztályban, amelyeket úgy kaphatunk, hogy a mintának
‐ a legkisebb sorszámú teljes blokkban, legyen ez a b-edik ‐ amelyből legalább
 egy elemet tartalmaz, de nem az összeset ‐ levő elemeit elforgatjuk;
‐ a magasabb sorszámú blokkokban lévő ‐ tehát a bm-nél nagyobb ‐ elemeit
 tetszés szerint megváltoztatjuk arra vigyázva, hogy bm-nél nagyobbak marad-
 janak.
 

Ha megmutatjuk, hogy bármelyik ilyen osztályban a k-asok összegét m-mel maradékosan elosztva a 0,1,...,m-1 maradékok mindegyikét ugyanannyiszor kapjuk meg, készen vagyunk: ugyanez igaz lesz az összes k-asra is.
Hívjuk egész számok egy véges H halmazát modd egyenletesnek, ha minden, a H elemeit d-vel osztva fellépő maradék ugyanannyiszor fordul elő, és teljesen egyenletesnek, ha a 0,1,...,d-1 maradékok mindegyike ugyanannyiszor fordul elő. Ha pl. H minden eleme egyenlő és d>1, akkor H egyenletes, de nem teljesen egyenletes modd. Így azt kell megmutatnunk, hogy az egy osztályba eső k-asok összegeinek halmaza teljesen egyenletes modm.
Tartalmazzon a minta T darab elemet a b-edik blokkból (0<T<m), a b-nél nagyobb sorszámú blokkokban pedig legyen összesen k' eleme (0<k'<k). Szükségünk lesz az m és a T legnagyobb közös osztójára ‐ legyen ez q ‐ és a relatív prím p=T/q és t=m/q mennyiségekre. Jelölje még n' a b-edik blokk utáni blokkok elemszámának összegét, azaz legyen 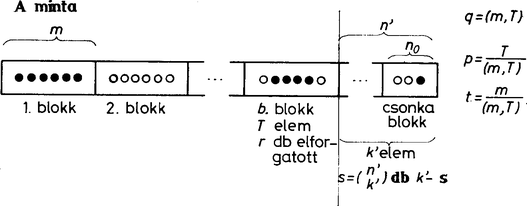n'=n-bm.
 
 
2. ábra
 

A minta bm-nél nagyobb k' darab elemét (n'k')=S féleképpen rendezhetjük át, ezekben az elemek összegei legyenek y1,y2,...,yS.
Mivel q osztója m-nek, ezért n'≡n(modq). Másfelől az első b darab blokk mindegyikében 0,m vagy T ‐ azaz q-val osztható ‐ a minta elemeinek száma, ezért k'≡k(modq). Így n'(modq)=n(modq) és k'(modq)=k(modq).
 

A minta osztályában a b-edik blokk utáni elemeken tulajdonképpen egy másik játék zajlik: itt n' szomszédos egész közül választunk ki minden lehetséges módon k' darabot. Azt állítjuk, hogy ez a játék q résztvevő között igazságos, azaz az {y1,y2,...,yS} halmaz teljesen egyenletes modq.
Ehhez nyilván elég megmutatnunk hogy a J(q,n',k') játék igazságos, ami viszont az indukciós feltevésből következik. Ez alkalmazható, mert q≤T<m, másrészt a J(q,n',k') játékra teljesül a Feltétel: ha d a q-nak 1-nél nagyobb osztója, akkor a q|m miatt d|m, így a J(m,n,k) játékra felírt Feltételből k(modd)>n(modd). Másfelől d|q -ból és n≡n'(modq)-ból
n(modd)=n'(modd)
és hasonlóan k≡k'(modq)-ból
k(modd)=k'(modd)
adódik, vagyis valóban
k'(modd)>n'(modd)
A játéknak a b-edik blokk utáni q személyes részére tehát valóban teljesül a feltétel, így az igazságos, és vegyük észre, hogy megszabadultunk a kellemetlen csonka blokktól.
 

Nézzük ezután az egy osztályba eső k-asoknak az első b blokkba eső részét. Ha a minta b-edik blokkbeli elemeinek r darab elforgatott képe van (r≤m), akkor ezeket előállítják a 0,1,2,...,(r-1) mértékű forgatások. Azt állítjuk, hogy ekkor p=T/(m,T) osztója r-nek.
Ha az i mértékű forgatás után a bm-nél nem nagyobb elemek összege xi (i=0,1,2,...,r-1), akkor az elforgatás tulajdonságai alapján
xi≡x0+iT=x0+itq(modm).
Mivel pedig az r mértékű elforgatás eredeti állapotába viszi a b-edik blokkot, x0≡x0+rtq(modm), azaz m=pq osztója rtq-nak, vagyis p osztója rt-nek. Mivel p és t relatív prímek, ezért valóban p|r.
Hogyan írhatjuk fel ezután egy, a mintával egy osztályban lévő k-as elemeinek az összegét? A bm-nél nem nagyobb elemek összege a b-edik blokk elforgatásai révén x0,x1,...,xr-1 valamelyike, a bm-nél nagyobbak összege pedig y1,y2,...,yS valamelyike. A k-asok összegei tehát az xi+yj(i=0,1,..., ...,r-1,j=1,2,...,S) alakú összegek lesznek, mert teljesen függetlenül választhatjuk i-t és j-t.
Az állítást ezzel a következő segédtételre vezettük vissza:
 

Egy segédtétel
 

Ha m=pq,r,S,t pozitív egészek, p és t relatív prímek, p osztója r-nek, x0,x1,...,xr-1 olyan egész számok, amelyekre xi≡x0+itq(modm) ‐ tehát valamennyien ugyanazt a maradékot adják q-val osztva ‐ végül az {y1,y2,...yS} teljesen egyenletes modq, akkor az xi+yj(i=0,1,...,r-1;j=1,2,...,S) alakú összegek halmaza is teljesen egyenletes modm
A segédtétel csak első ránézésre tűnik ijesztőnek. Először is vegyük észre, hogy az {x0,x1,...,xr-1} halmaz is egyenletes modm.
Tudjuk ugyanis, hogy p|r, osszuk be tehát az r darab xi-t p elemű csoportokba: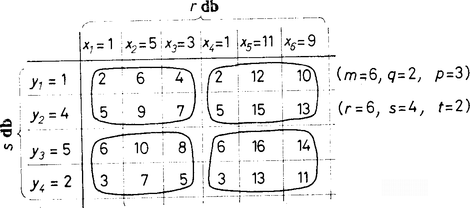
(x0,x1,...,xp-1),(xp,xp+1,...,x2p-1),...(xr-p,...,xr-1),
Mivel xi≡x0+itq(modm),m=pq, ezért az
xi≡xj(modm)
feltételből a q-val való osztással
it≡jt(modp)
adódik. Ez utóbbi pedig (t,p)=1 miatt akkor és csak akkor igaz, ha i≡ ≡j(modp). Az egyes csoportokon belül így nincsenek egyenlő maradékok, ezek p-esével ismétlődnek, így minden fellépő maradék annyiszor fordul elő, ahány csoport van: r/p-szer.
 
 

Vegyük szemügyre ezután a táblázatot. Itt négy (Sq⋅rp) darab teljes maradékrendszer elemei állnak mod6(m=6). Ezeket úgy kapjuk, hogy az y-okból egy-egy teljes modq maradékrendszer elemeihez ‐ az {y1,y2,...,yS} halmaz Sq darab ilyenre bontható ‐ hozzáadjuk az m szerint különböző maradékot adó x-ek egy-egy p elemű csoportjának az elemeit ‐ ilyen csoport r/p darab van.
Elég tehát belátnunk, hogy ha a q elemű Y halmaz teljes maradékrendszer modq, a p elemű X halmaz elemei pedig valamennyien ugyanazt a maradékot adják q-val osztva, de m-mel osztva bármely kettő különböző maradékot ad, akkor az x+y(x∈X,y∈Y) alakú összegek teljes maradékrendszert alkotnak modm.
Mivel összesen p⋅q=m darab ilyen összeg van, ezért azt kell megmutatnunk, hogy semelyik kettő nem adhat ugyanolyan maradékot m-mel osztva.
Ez viszont nyilvánvaló, hisz ha
x'+y'≡x''+y''(modm),(*)
akkor m=pq miatt a fenti kongruencia (modq) is fennáll, és mivel bármely két x ugyanazt a maradékot adja q-val osztva,
y'≡y''(modq),
ami csak úgy lehet, ha y'=y'', hiszen az y-ok teljes maradékrendszert alkottak modq. Ekkor viszont (*)-ból
y'≡y''(modm)
adódik, ami az x-ek kiválasztása miatt (modm különböző maradékot adtak) csak az x'=x'' esetben lehetséges.
Ezzel a felhasznált segédtételt bebizonyítottuk és így a Feltétel elégséges voltának bizonyítása teljes.
 

Kísérlet a megfordításra
 

Most visszavezetjük a Feltétel szükségességét arra az állításra, hogy ha n<m esetén nem teljesül, akkor J(m,n,k) nem igazságos (kivéve, ha m=1).
Ideje kimondani egy apró segédtételt, amit tulajdonképpen már ismerünk és a csapatokba rendezés módszerével be is bizonyítottunk:
Ha J(m,n,k) igazságos és m' osztója m-nek, akkor J(m',n,k) is igazságos.
Tegyük fel ezután, hogy a J(m,n,k) játékra nem teljesül a Feltétel. Legyen m' az m legkisebb 1-nél nagyobb osztója, amely a feltételt elrontja, tehát amellyel osztva a k legfeljebb akkora maradékot ad, mint az n. A fenti segédtétel alapján ekkor elég bebizonyítani, hogy J(m',n,k) nem igazságos.
Az m' kiválasztása miatt ha 1<d<m' és d osztója m'-nek (tehát m-nek is), akkor k a d-vel osztva már nagyobb maradékot ad, mint az n, ezért elég a következőt igazolni:
Ha az m minden d osztójára, amelyre 1<d<m, a k nagyobb maradékot ad d-vel osztva, mint az n, de az m-re ez már nem igaz, tehát k(modm)≤n (modm), akkor J(m,n,k) nem igazságos.
Bontsuk fel az első n pozitív egészet m-elemű blokkokra úgy, mint az elégségesség bizonyításánál tettük és tekintsük azokat a szám k-asokat, amelyekhez találhatók olyan teljes blokkok, amelyekből legalább egy, de legfeljebb m-1 elemet tartalmaznak.
Az indukciós lépéshez teljesen hasonlóan kapjuk, hogy ezekben az elemek összegét m-mel elosztva minden lehetséges maradék ugyanannyiszor fordul elő, így ezeken a játék igazságos.
A többi k-as ezután olyan, hogy minden teljes blokkból vagy az összes elemet tartalmazza, vagy egyet sem. Legyen egy ilyen k -asnak k0 eleme az n0 elemű csonka blokkban. Ekkor k0≡k(modm), mert k-k0 osztható m-mel (a teljes blokkban lévő elemek száma), másrészt k0≤n0<m, ami csak úgy lehet, hogy k0 az a maradék, amelyet k ad m-mel osztva.
A fennmaradó k-asok tehát olyanok, hogy a teljes blokkok közül [k/m]-et tartalmaznak, a csonka blokkból pedig k0 elemet.
A teljes blokkban levő elemek összege m-mel osztva mindig ugyanannyi maradékot ad; legyen ez r.
Az ilyen k-asokon zajló játékot úgy is felfoghatjuk, mintha az csak a csonka blokkon belül folyna, innen kellene k0 elemet kiválasztani. (Az eredeti játékban k0 ilyen elem összegéhez még r-et hozzá kell adnunk és minden ilyen k0-ast ([n/m][k/m])-féleképpen ki kell egészítenünk [k/m] teljes blokkal, de ez a játék igazságos voltán nem változtat, J(m,n,k) akkor és csak akkor igazságos, ha a ,,csonka blokkban'' zajló J(m,n0,k0) az.
Elég tehát J(m,n0,k0)-ról bebizonyítani, hogy nem igazságos, ebben pedig valóban n0<m.
Ha m=pα, ahol p prím és α pozitív egész, akkor a bizonyítás könnyen befejezhető egy ismert számelméleti eredmény felhasználásával:
Ha pα|(nk), akkor pα≤n.
Ha ugyanis ilyenkor J(pα,n,k) igazságos, akkor az (nk) darab k-asban az elemek összegét pα-val osztva minden maradék ugyanannyiszor fordul elő, így pα osztója (nk)-nak. Mivel pedig ez nem teljesülhet, ha n<pα, ilyenkor J(pα,n,k) valóban nem igazságos.
A módszer az általános esetben ezen a ponton (n<m) elakad: nem látni reményt, hogy tovább lehetne lépni vele.
Jelenlegi alakjában is alkalmas viszont más számelméleti feladatok megoldására:
 

Egy következmény
 

Ha n=nSnS-1...n1n0¯ és k=kSkS-1...k1k0¯
egy p alapú számrendszerben felírva, ahol p prímszám, akkor
(nk)≡(n0k0)(n1k1)...(nSkS)(modp),
ahol az (ab) binomiális együtthatóban megengedjük a b>a esetet is; ilyenkor (ab)=0.
Az eredmény Lucas lemma néven ismert és messzemenő általánosítása annak az F. 2597. feladat megoldásában kimondott állításnak (KÖMAL 1987/3 108. o.), mely szerint (nk) akkor és csak akkor páratlan, ha az n-et és a k-t kettes számrendszerben felírva mindazokon a helyiértékeken, ahol a k-ban 1-es áll, az n-ben is 1 áll.
A bizonyításhoz nyilván elég megmutatni, hogy
(nSnS-1...n1n0kSkS-1...k1k0¯)≡(nSnS-1...n1kSkS-1...k1¯)⋅(n0k0)(modp).

Ha k0>n0, akkor J(p,n,k) igazságos és így p|(nk), valamint (n0k0)=0 miatt az állítás igaz. Ha k0≤n0, akkor (nk) kongruens modulo p azoknak a J(p,n,k)-beli szám k-asoknak a számával, amelyek az nSnS-1...n1¯=[n/p] teljes blokk közül [k/p]=kSkS-1...k1¯ darabot teljes egészében, az n0 elemű csonka blokkból pedig k0 darab elemet tartalmaznak. A többi k-asokon, mint láttuk, a játék igazságos, így azok száma osztható p-vel.
Az ilyen k-asok száma pedig éppen
(nSnS-1...n1kSkS-1...k1¯)⋅(n0k0).

Ezzel az állítást igazoltuk.