Cím:	Osztójátékok
Szerző(k):	Varga Tamás
Füzet:	1988/január, 2 - 7. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. OSZTÓJÁTÉK${}^{*}$ Kezd már átmenni a köztudatba, hogy tanulás és játék között nincs olyan merev határvonal, mint régebben hittük. Mondjuk inkább így: nem kellene olyan merev határvonalnak lennie, mint amilyent ma is gyakran húzunk köztük. A tanulás és a játék éles szétválasztása, sőt szembeállítása olyanféle elképzelésekből táplálkozik, hogy a gyerek nem szeret tanulni, de rá kell szorítani, hogy tanuljon. Miután eleget tett kellemetlen kötelességének, arra is sor kerülhet, hogy valami kedve szerint valóval foglalkozzon: játsszon. A korszerű pedagógia sok területen igyekszik összekapcsolni a tanulást és a játékot. Annak a sok energiának egy részét, amit a hagyományos pedagógia a játékosság elfojtására fordított, az új pedagógia inkább a játékosságnak a tanulás szolgálatába állításával hasznosítja. A tárgykörtől és a gyerekek életkorától függően sokféle játékkal lehet előrevinni és egyben a gyerek számára kedvesebbé tenni a matematika tanulását. Kisebb gyerekek tanításában ez rendszerint munkaeszközökkel végzett manuális tevékenységet jelent, nagyobb gyerekeknél egyre inkább szavak vagy jelek közegében folyó, nagyobb mértékben gondolati játékokat. Az utóbbiakra látunk most egy példát. Ez a játék az osztó, többszörös, oszthatóság, törzsszám stb. fogalmak elmélyítésére szolgál. Alkalmas arra, hogy a gyerekek általános összefüggéseket vegyenek észre a segítségével (egy szám törzstényezős alakjának típusai). Önmagában is érdekes, mint játék, amellett játékelméleti érdekessége is van, mint arról később lesz szó. A játékot ketten játsszák. A két játékos megállapodik egy (pozitív egész) számban. Ezt felírják, pl. $\begin{array}{c}{\displaystyle \begin{array}{|c|}\hline \text{26}\\ \hline\end{array}\mathrm{.}}\end{array}$ Ennek a számnak az osztóit a két fél felváltva írja, például $\begin{array}{c}{\displaystyle \mathrm{1,}\mathrm{13,}\mathrm{2,}26.}\end{array}$ Veszít, aki már nem tud más osztót mondani, mint magát az először felírt számot, itt a $26$-ot. Ez így eddig túl egyszerű játék volna. Ha páros számú osztója van egy számnak (mint ahogy a $26$-nak négy osztója van), akkor elvben mindig a kezdő nyerne; ha páratlan, akkor a másik, és a játék semmi más ügyességet vagy tudást nem kívánna, csak a felírt szám osztóinak ismeretét. A játék igazi érdekességét a következő szabály adja meg: az addigi számok osztóit nem szabad írni. Ez persze a játék elején felírt számra nem vonatkozik, csak azokra, amiket játék közben felváltva írtak. Az először felírt számnak éppenhogy minden szám, amit a játék közben írnak,osztója kell hogy legyen. A többinek viszont nem lehet osztója olyan szám, amit utána valamikor írnak, akár közvetlenül utána, akár később. A közös játék szakaszában kiindulhatunk először egy sok osztójú számból, mint pl. $60$, hogy mindjárt először lássanak meg valamit a játék bonyodalmaiból és így érdekességéből. Nem fogadjuk el a módszereskedő pedagógiának azt az alapelvét, hogy mindig az egyszerűtől a bonyolult felé kell haladnunk! Az olyan bonyodalmat, ami nem ijeszt el, hanem kedvet csinál, nem kerüljük. Ahhoz azonban, hogy a játék lehetőségeit ki tudják elemezni, stratégiákat tudjanak kidolgozni, később mégis jó bizonyos egyszerű típusokat elővenni. Lássuk pl. a játékot $6$-tal: $\begin{array}{c}{\displaystyle \begin{array}{|c|}\hline \text{6}\\ \hline\end{array}\mathrm{2,}\mathrm{3,}6.}\end{array}$ Most a kezdő vesztett. Pedig, ha ügyes, nyerhetett volna: $\begin{array}{c}{\displaystyle \begin{array}{|c|}\hline \text{6}\\ \hline\end{array}\mathrm{1,}\mathrm{3,}\mathrm{2,}6.}\end{array}$ Ha $1$-et ír, akkor a másik akár $2$-t ír, akár $3$-at, ő írja a másikat és nyert, mert akkor már csak $6$-ot lehet írni. Az ilyen alakú, általánosan kifejezve $pq$ alakú számoknak mindig $4$ osztójuk van, és mindig a kezdő nyer bennük. A nyerő stratégia mindig az, hogy $1$-gyel kezdik, és ha ellenfelük az egyik törzsszámosztót mondja, ők erre a másikkal válaszolnak, $p$-re $q$-val, $q$-ra $p$-vel. Ellenfelüknek akkor nem marad más, mint $pq$, és elvesztette a játékot. A legegyszerűbb eset: a törzsszámok ($p$ típus). A játék ennyiből áll például: $\begin{array}{c}{\displaystyle \begin{array}{|c|}\hline \text{7}\\ \hline\end{array}\mathrm{1,}7.}\end{array}$ A kezdő $1$-et mond, és már meg is nyerte. Egy másik egyszerű típus: törzsszámok $1$-nél nagyobb kitevőjű hatványai ($p^n$ típus). Ebben a típusban az eddigiekhez képest az az új, hogy nem az $1$-gyel való kezdés a legjobb lépés. A $p$ és a $pq$ típusnál ugyanis $1$-gyel érdemes kezdeni. A $p^n$ típusnál viszont mindig az eggyel alacsonyabb hatvány,$p^{n-1}$ a jó kezdés. Lehet, hogy már előbb, a törzsszámokkal kapcsolatban eszébe jut valakinek, hogy mi van akkor, ha $\begin{array}{|c|}\hline \text{1}\\ \hline\end{array}$ a kiindulás. Ez a játék újabb adalékot szolgáltat ahhoz, hogy $1$ másképpen viselkedik, mint a törzsszámok; nem érdemes törzsszámnak tekinteni. Ha a felírt szám törzsszám, akkor aki $1$-et ír, nyer. Ha azonban a felírt szám $1$, akkor a kezdő nem írhat mást, csak $1$-et és veszített. Ehhez a típushoz meg lehet próbálni úgy elvezetni a gyerekeket, hogy alkalmas pillanatban felvetjük a kérdést, ki tud olyan számot javasolni, aminél a kezdő veszít. Fogalmazhatja a tanár így is: "Most én szeretnék kezdeni. Mondjátok meg, mit írjunk föl. Tudnátok-e olyan számot mondani, hogy biztosan ti nyerjétek meg a játékot?'' (Lehet, hogy a gyerekek nem az $1$-et mondják, hanem más számmal próbálkoznak. Még az is lehet, hogy sikerül minket ilyen módon megverniük. Látni fogjuk később, hogy ebben a játékban az, aki kezd, ha elég ügyes, mindig megnyerheti a játékot, kivéve, ha az alapul vett szám az $1$.) Ezek a példatípusok és néhány spontán felmerülő bonyolultabb típusú példa időszerűvé teheti a számok osztóinak a hálóelméletből ismert Hasse-féle diagrammal való szemléltetését. Legfölülre írjuk azt a számot, amelynek az osztóiról szó van, legalulra az $1$-et. A közbülső "emeleteken'' helyezkednek el a szám valódi osztói. Az első emeleten lesznek a prímtényezők (az osztók közül a törzsszámok). Azt mondhatjuk, hogy az "első emeleti számokat'' a "földszinti számból'' (az $1$-ből) törzsszámmal való szorzás útján kapjuk. A "második emeleten'' azok a számok lesznek, amelyeket az "első emeleti'' számokból kapunk törzsszámmal való szorzás útján. És így tovább. Azokat a számokat, amelyek egymásból törzsszámmal való szorzás (illetve osztás) útján keletkeznek, vonallal kötjük össze. Egy példa az 1. ábrán látható.     1.a ábra 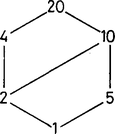      1.b ábra   Ez az ábrázolási mód szemléletessé teszi, hogy az egyforma típusú számoknál miért ugyanaz a nyerő stratégia. $12$ és $20$ ‐ mint az ábrák is mutatják ‐ egyforma típusúak. Típusuk $p^{2}q$. ($12=2^2\cdot 3$, $20=2^2\cdot 5$.) Mindkét esetben $1$ a jó kezdés. Utána az ellenfél bármelyik számot mondja (persze nem a $12$-t vagy $20$-at), mi ugyanazon az emeleten levő másik számmal válaszolunk. Ezt mindig megtehetjük, és végül ellenfelünk veszít. Ez a stratégia $p^{n}q$ esetben mindig biztosítja a győzelmet, nemcsak $p^{2}q$ esetben. Ha ettől a stratégiától eltér a kezdő fél, ellenfele megnyerheti a játékot. Ha például $1$ helyett valami mást írunk, akkor ellenfelünk ennek a párját írja, és attól kezdve követi ezt a stratégiát, amit különben mi követtünk volna. Ugyanígy akkor is, ha később térünk el a stratégiától. Ez mindig igaz: ha az egyik fél eltér a helyes stratégiától, akkor a másik azonnal átveheti ugyanazt a stratégiát, és ha csak ő is nem hibázik a játékban, nyerhet. Ez egyszerű esetekben egészen világos. Ha például prímszám hatványáról van szó, akkor a Hasse-diagram egyetlen szálból áll. Ha a kezdő fél elfoglalja az utolsó előtti emeletet, akkor nyert. Ha nem, akkor ellenfele foglalja el, és ő nyert. A $p^n$ és $p^{n}q$ típusoknál a helyes stratégiát egyszerűen le lehet írni. Más esetekben különféle bonyodalmak lépnek fel. Már a $p^2{q}^2$ eset (például $36=2^2\cdot 3^2$, $100=2^2\cdot 5^2$) sem egészen egyszerű. A stratégiáról általánosságban csak annyit mondhatunk: a kezdőnek mindig van nyerő stratégiája (kivéve, ha $1$ az eredeti szám), de hogy miben áll ez a stratégia, azt esetenként kell eldöntenie. Honnan lehet tudni, hogy az, aki kezd, ha elég ügyes, mindig nyerhet? Először is gondoljuk meg, hogy vagy a kezdőnek, vagy a másodszor lépőnek biztosan van nyerő stratégiája, vagyis a játék elvben már el is dőlt, mihelyt felírták a számot, és megállapodtak abban, hogy ki kezd. Nemcsak erre a játékra láthatjuk be, hogy kezdéskor elvben már el is dőlt, hanem minden olyan játékra, amelyben két játékos felváltva lép, mindig véges számú lépés közül választhat, és a játék véges számú lépés után mindig befejeződik egy olyan játékhelyzettel, amely vagy az egyik, vagy a másik játékos számára győzelmet jelent. (Ha döntetlen helyzetek is lehetnek, mint például a sakkban, akkor azt bizonyíthatjuk be, hogy vagy a kezdő számára, vagy a másodszor lépő számára van nyerő stratégia, vagy pedig bármelyik számára van olyan stratégia, amelynek segítségével döntetlent érhet el. Ez azt jelenti, hogy minden sakkparti is elvben eldőlt abban a pillanatban, amikor kiderült, hogy melyik játékos kezd, "csak éppen'' nem ismerjük azt a stratégiát, amellyel valamelyik fél győzhetne, vagy döntetlent érhetne el, sőt még azt sem tudjuk, hogy győzelmet lehet-e elérni feltétlen biztonsággal, vagy csupán döntetlent és ha győzelmet, akkor melyik színnel. Az alábbi gondolatmenetet csak kevéssel kell módosítani, hogy az ilyen játékokra is alkalmazható legyen.) Tudjuk, hogy minden véghelyzet vagy a kezdő számára (nevezzük világosnak), vagy a másodszor lépő számára (nevezzük sötétnek) nyerőhelyzet. Be akarjuk látni, hogy minden más helyzetről is ugyanezt mondhatjuk, a kezdőhelyzetet is beleértve; vagyis minden játékhelyzetről eldönthető vagy az, hogy a világos, vagy az, hogy a sötét győzelmet érhet el, bármiket lép a másik. Nézzük először azokat a helyzeteket, amelyekből egy lépés után bármit lépünk is, véghelyzethez jutunk. Ha egy ilyen helyzetben az, akin a lépés sora van, el tud érni számára nyerő helyzetet, akkor ez is nyerőhelyzet. Ugyanígy visszafelé haladva, azokról a helyzetekről is el tudjuk dönteni, hogy a világos vagy sötét számára nyerőhelyzetek-e, amelyekből egy lépésben ugyan nem jutunk feltétlenül véghelyzethez, de két lépésben igen. És így tovább. Így végül a kezdőhelyzetről is eldől, hogy melyik számára jelent nyerőhelyzetet. Ez a bizonyítás konstruktív bizonyítás: megmondtuk, hogyan lehet eldönteni a véghelyzetekből kiindulva, hogy a kezdőhelyzet melyik fél számára nyerőhelyzet. (Más kérdés, hogy ezt az eljárást az esetek nagy száma miatt a gyakorlatban végre tudjuk-e hajtani.) Térjünk vissza az eredeti számelméleti játékhoz. Eddig elemzett speciális eseteiben (egy kivételével) világosnak mindig volt nyerő stratégiája. A fenti tétel alapján ezt így is mondhatjuk: mindig a világosnak volt nyerő stratégiája, hiszen azt már tudjuk, hogy valamelyiknek kellett, hogy legyen. Azt állítjuk, hogy minden más esetben is a világosnak van nyerő stratégiája. Tegyük fel, hogy valamilyen $N$ szám esetében a sötétnek volna nyerő stratégiája, vagyis bármivel kezd is a világos, és bárhogyan lép is később, a sötét mindig tudja úgy folytatni, hogy végül a világos kénytelen kimondani $N$-et. Tegyük fel, hogy abban az esetben, ha a világos $1$-gyel kezd, a sötét stratégiájának nyerő lépése (vagy egyik nyerő lépése) egy bizonyos $n$ szám kimondása. Ezzel azonban máris találtunk egy nyerő stratégiát a világos számára, ő kezd ezzel az $n$-nel, és továbbra is a sötét előbbi stratégiája szerint folytatja a játékot. Abból a feltételezésből, hogy a sötétnek van nyerő stratégiája, ellentmondásra jutottunk, hiszen nem lehet mindkettőnek nyerő stratégiája. A kezdőhelyzet ennélfogva a világos számára nyerőhelyzet, hiszen kettőjük közül valamelyiknek biztosan van nyerő stratégiája. Bizonyításunk a világos nyerő stratégiáját nem adja meg, csak a létezését igazolja azzal, hogy az ellenkező feltevésből ellentmondást vezet le. Ez a bizonyítás nem konstruktív bizonyítás, hanem ún. tiszta egzisztencia-bizonyítás. Ezt az eléggé nehéz, absztrakt gondolatmenetet szemléletessé tehetjük egy új ábrázolásmód segítségével. Egy-egy játék összes játéklehetőségeit "fával'' ábrázoljuk. A fa alul annyifelé ágazik, ahány kezdő lépés van. Minden ága annyifelé ágazik tovább, ahányfélét az ellenfél válaszként léphet arra és így tovább. Ha valakinek a lépésére a másik már semmit sem tud lépni, akkor az ág véget ér. Minden ilyen ágvégződés a játék egy lehetséges befejezését jelenti, és a fa aljától odáig vezető (egyetlen!) vonal a játék menetét jellemzi. Minden befejezésről ─ és így minden játékról ─ a játékszabályok alapján tudjuk, hogy melyik fél számára jelent győzelmet. Ezt az ágvégződésnél feltüntetjük. (Az osztójátéknál ez nem feltétlenül szükséges, mert a szabályai olyanok, hogy aki utoljára lépett, az vesztett. Más játékoknál vagy fordítva van, vagy nem ez, hanem valami más szempont dönti el, ki nyert.) A fa felfelé menő ágai felváltva a világos és a sötét lépéseit jelentik. Ábráinkon jobb áttekinthetőség kedvéért $v$ és $s$ betű jelzi, hogy adott magasságokban levő ágak a világos vagy a sötét lépéseit jelentik-e. Ábrázoljuk így a $6$ kiindulású osztójátékot. Négy kezdő lépés lehetséges: $\mathrm{1,}\mathrm{2,}\mathrm{3,}6$. Aki annyira értelmetlen, hogy $6$-ot lép, az már el is veszítette a játékot, ellenfele győzött. A többi esetben folytatódik a játék. A legalsó ágakat a 2. ábra mutatja.     2. ábra   Sötét karikával jelképezzük azt, hogy a negyedik esetben a sötét győzelmével véget ért a játék. Az $1$-re háromféle válaszlépés lehetséges $(2$, $3$, $6)$, a $2$-re kétféle ($3$ és $6$), a $3$-ra is ($2$ és $6$), a $6$-ra már egy sem. Az utolsó eset mindenütt a játék végét, de most a világos győzelmét jelenti (világos karikák, 3. ábra).     3. ábra   A következő lépésben megint tovább megy az elágazás, és két esetben még egy-egy lépés lehetséges (4. ábra).     4. ábra   Látjuk, hogy összesen $10$ ágvégződés van, és mindegyikhez egy pontosan meghatározott úton juthatunk el legalulról fölfelé haladva. Ezek az ágvégződések és egyúttal ezek az utak ennek a játéknak tízféle lehetséges lefolyását ábrázolják. A gyakorlatban ezek nem szoktak mind előfordulni, hiszen aki egy kicsit is megértette a játékszabályokat, az nem tesz olyan értelmetlenséget, hogy ha nem kell, $6$-ot ír. A teljesség kedvéért most mégis minden esetet feltüntettünk, ezeket is. Ábráink alapján nyomon követhetjük annak a bizonyítását, hogy a játék sorsa a játék kezdetekor már eldőlt. A "színezett'' végpontokból visszafelé haladva a többi csomópontot is színezzük a következő elv alapján: 1. Ha nincs elágazás, akkor a karika színe ugyanaz, mint a következő karikáé. 2. Ha elágazás van, de a lehetséges folytatásokban mindenütt ugyanolyan színű karika van, akkor szintén "nincs mit tenni'', marad a szín. 3. Ha azonban többféle szám között lehet választani, akkor az éppen soron levő játékos a számára kedvezőbb lehetőséget választja, vagyis ha a világos lép, világos lesz a karika, ha a sötét lép, akkor sötét. Ennek alapján mechanikusan végigszínezhetjük a csomópontokat az ágak végpontjaiból a fa tövéig. A játszma kezdetéhez (alulra) világos karikát írtunk, mert fölülről lefelé haladva kiderült, hogy aki kezd, akármit lép is a másik, tud úgy lépni, hogy végül is ő nyerjen (világos karikához jussunk). A helyes kezdő lépést nyíl mutatja. 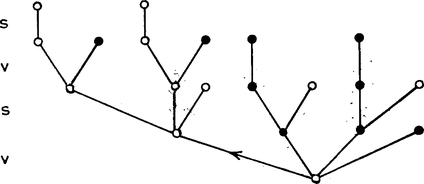    5. ábra   A most bevezetett ábrázolásmódot más játékok ábrázolására is felhasználhatjuk. Persze, csak egészen egyszerű játékokat tudunk így ábrázolni, különben a "fa'' áttekinthetetlenül bonyolult lesz. Például a sakkjátékban $20$ kezdőlépés van, vagyis a fának $20$ főága; mindegyikre $20$ válaszlépés, vagyis mind a $20$ ág még $20$ felé ágazik ($400$ ág már a második lépésnél). A pontos ábrázolás ilyenkor gyakorlatilag keresztülvihetetlen. Viszont azok a gondolatok, amelyek egyszerű játéktípusok ábrázolásakor megformálódnak a gyerekekben, a bonyolult játékokra is alkalmazhatók, és segítik a megértést. ${}^{*}$Az Élő matematika (Tankönyvkiadó, Budapest, 1975.) című kiadványban megjelent tanulmány rövidített változata.