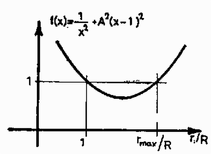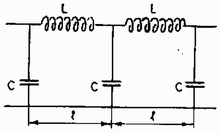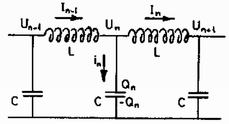Cím:	Az 1987. évi (18.) Nemzetközi Fizikai Diákolimpia feladatai
Szerző(k):	Gnädig Péter
Füzet:	1987/november, 401 - 413. oldal	PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Elméleti feladatok   1. feladat. Nedves levegő adiabatikusan áramlik át egy hegyláncon (lásd az 1. ábrát!). 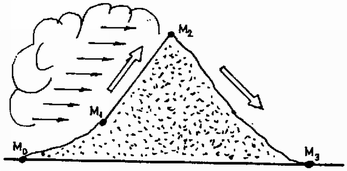    1. ábra   Az $M_0$ és $M_3$ meteorológiai állomásokon 100 kPa légnyomást mérnek, míg az $M_2$ állomáson a nyomás 70 kPa. A levegő hőmérséklete $M_0$-nál $20{}^{\circ }$C. Miközben a levegő emelkedik, $84\mathrm{,}5\text{ kPa}$-nál felhőképződés indul meg. A hegyen felfelé emelkedő nedves levegő mennyiségét úgy írhatjuk le, hogy megadjuk: minden négyzetméter földfelület fölött 2000 kg nedves levegő található. A nedves levegő 1500 másodperc alatt éri el a hegygerincet (az $M_2$ állomást). Az emelkedés alatt minden kilogram levegőből $2\mathrm{,}45\text{ g}$ mennyiségű víz válik ki eső formájában.   1. Határozd meg a felhőképződés magasságához tartozó $T_1$ hőmérsékletet!   2. Mekkora a felhőképződés kezdetének $h_1$ magassága az $M_0$ állomáshoz képest? (Tételezzük fel, hogy a légkör sűrűsége a magassággal lineárisan csökken!)   3. Mekkora $T_2$ hőmérsékletet mérnek a hegygerincen?   4. Számítsd ki, hogy mennyi (milyen magas vízoszlopnak megfelelő) eső esik 3 óra alatt, feltéve hogy az eső egyenletesen esik az $M_1$ és $M_2$ pontok között!   5. Mennyi a hegylánc mögötti $M_3$ állomáson mérhető $T_3$ hőmérséklet? Diszkutáld, hogy mennyiben más a légkör állapota az $M_3$ állomásnál az $M_0$-beli állapothoz képest!   Útmutatások és adatok: A légkör ideális gáznak tekinthető. Hanyagoljuk el a vízgőz befolyását a fajhőre és a levegő sűrűségére, továbbá ne vegyük figyelembe a párolgáshő hőmérsékletfüggését se. A hőmérsékleteket 1 K-es pontossággal, a felhőképződés helyét 10 m-es pontossággal, a lehulló eső mennyiségét pedig $0\mathrm{,}1$ mm-es pontossággal határozzuk meg! A légkör fajhője a vizsgált hőmérséklettartományban: $\begin{array}{c}{\displaystyle c_p=1005\text{ J}\cdot {\text{kg}}^{-1}\cdot {\text{K}}^{-1}\mathrm{.}}\end{array}$ Az $M_0$ állomáson a légkör sűrűsége $p_0$ és $T_0$ értékeknél: $\begin{array}{c}{\displaystyle {\varrho }_0=1\mathrm{,}189\text{ kg}\cdot {\text{m}}^{-3}\mathrm{.}}\end{array}$ A víz párolgáshője a felhőben: $\begin{array}{c}{\displaystyle q_v=2500\text{ kJ}\cdot {\text{kg}}^{-1}\mathrm{,}}\end{array}$ továbbá Megoldás.   1. Az adiabatikus tágulás során a nyomás és a térfogat között a $\begin{array}{c}{\displaystyle p_0\cdot V_0^{\varkappa }=p_1\cdot V_1^{\varkappa }}\end{array}$ összefüggés áll fenn. Emellett igaz, hogy $\begin{array}{c}{\displaystyle \frac{p_0{V}_0}{T_0}=\frac{p_1{V}_1}{T_1}\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle T_1=T_0{\left(\frac{p_1}{p_0}\right)}^{1-\frac{1}{\varkappa }}=239\text{ K}\cdot 0\mathrm{,}{845}^{0\mathrm{,}286}=279\mathrm{,}4\text{ K}\mathrm{.}}\end{array}$ 2. A légnyomás változása $h_1$ magasságig $\begin{array}{c}{\displaystyle p_0-p_1=\overline{\varrho }\cdot g\cdot h_1\mathrm{,}}\end{array}$ ahol $\overline{\varrho }$ az átlagsűrűséget jelöli. Mivel a légkör sűrűsége a feltevésünk szerint a magassággal lineárisan változik, $\begin{array}{c}{\displaystyle \overline{\varrho }=\frac{{\varrho }_0+{\varrho }_1}{2}\mathrm{,}}\end{array}$ ahol $\begin{array}{c}{\displaystyle {\varrho }_1={\varrho }_0\cdot \frac{p_1}{p_0}\cdot \frac{T_0}{T_1}=1\mathrm{,}054{\text{ kg/m}}^3\mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle \overline{\varrho }=1\mathrm{,}122{\text{ kg/m}}^3\mathrm{,}}\end{array}$ végül $\begin{array}{c}{\displaystyle h_1=\frac{p_0-p_1}{\overline{\varrho }\cdot g}=1408\text{ m}\mathrm{.}}\end{array}$ 3. A hegygerincen mérhető hőmérséklet nagyságát kétféle hatás befolyásolja. Egyrészt az emelkedés miatt a hőmérséklet lecsökken bizonyos $T_x$ értékre, másrészt a víz kicsapódásakor felszabaduló hő valamekkora $\Delta T$ értékkel felmelegíti a levegőt. $T_x$ az adiabatikus változás egyenletéből számolható ki: $\begin{array}{c}{\displaystyle T_x=T_1\cdot {\left(\frac{p_2}{p_1}\right)}^{1-\frac{1}{\varkappa }}=264\mathrm{,}8\text{ K}\mathrm{.}}\end{array}$ $\Delta T$-t a következőképpen határozhatjuk meg. A kondenzáció során a levegő minden kilogrammjában $q_v\cdot m$ hő szabadul fel, s ez $c_p\cdot \Delta T$-vel egyezik meg, ahol $m$ az 1 kg levegőből kiváló víz tömegét jelöli. Innen $\begin{array}{c}{\displaystyle \Delta T=\frac{q_v\cdot m}{c_p}=\frac{2500\text{ kJ/kg}\cdot 2\mathrm{,}45\text{ g/kg}}{1005\frac{\text{J}}{\text{kg}\cdot \text{K}}}=6\mathrm{,}1\text{ K}\mathrm{,}}\end{array}$ tehát végül $\begin{array}{c}{\displaystyle T_2=T_x+\Delta T=270\mathrm{,}9\text{ K}\approx 271\text{ K}\mathrm{.}}\end{array}$ 4. Mivel minden négyzetméter földfelület fölött 2000 kg nedves levegő található, ebben kilogrammonként $2\mathrm{,}45\text{ g}$ a víz, s ez a vízmennyiség 1500 s alatt esik le, másodpercenként $\begin{array}{c}{\displaystyle 2000\cdot 2\mathrm{,}45\text{ g/1500 s}=3\mathrm{,}27\text{ g}\mathrm{,}}\end{array}$ három óra alatt pedig összesen $\begin{array}{c}{\displaystyle 3\cdot 3600\text{ s}\cdot 3\mathrm{,}27\text{ g/s}=35\mathrm{,}3\text{ kg}}\end{array}$ eső esik. Tekintve, hogy 1 mm eső $1{\text{ kg/m}}^3$ vízmennyiségnek felel meg, az eső mennyisége $35\mathrm{,}3\text{ mm}$.   5. A hegy mögött a ‐ most már száraz ‐ levegő adiabatikusan áramlik, igaz tehát, hogy $\begin{array}{c}{\displaystyle T_3=T_2\cdot {\left(\frac{p_3}{p_2}\right)}^{1-\frac{1}{\varkappa }}=300\text{ K}\mathrm{.}}\end{array}$ Diszkusszió: Az $M_3$ állomásnál melegebb a levegő, mint a hegygerinc előtt fekvő $M_0$ állomásnál, bár a légnyomás mindkét helyen ugyanakkora. A hegyen átáramló nedves levegő szárazabb és melegebb lett; a hőmérsékletemelkedést a víz kicsapódása során felszabaduló hő okozta. Hasonló körülmények között áramló száraz levegőnél a hőmérséklet nem változna meg.   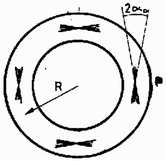2. feladat. Egy pontszerű $P$ elektronforrás elektronnyalábot bocsájt ki, amely egy toroid tekercs $\text{<span style="font-weight: bold;">B</span>}$ mágneses mezőjébe jut, az erővonalakkal megegyező irányban (2. ábra).     2. ábra   A nyaláb széttartásának szöge $2{\alpha }_0$, amelyről feltehető, hogy kicsiny (${\alpha }_0\ll 1$). Az elektronok $V_0$ gyorsítófeszültség alkalmazása után a toroid $R$ átlagos sugaránál jutnak be a tekercs belsejébe. $\text{<span style="font-weight: bold;">B</span>}$ nagyságát állandónak tekinthetjük, és az egyes elektronok közötti elektrosztatikus kölcsönhatást elhanyagolhatjuk.   1. Annak érdekében, hogy az elektronnyalábot a toroid belsejében tartsuk, bizonyos ${\text{<span style="font-weight: bold;">B</span>}}_1$ homogén mágneses eltérítő mezőt kell alkalmaznunk. Számítsd ki azt a $B_1$ értéket, amely ahhoz szükséges, hogy egy elektron $R$ sugarú körpályán mozogjon a toroidban!   2. A toroid terében négy, egymáshoz képest $\pi /2$-vel eltolt helyzetű fókuszpontot akarunk létrehozni az elektronnyalábban. Határozd meg, mekkora $B$ érték szükséges ehhez!   Megjegyzés: Az elektron pályájának vizsgálata során tekintsünk el a mágneses mező görbültségétől!   3. Ha a ${\text{<span style="font-weight: bold;">B</span>}}_1$ eltérítő mezőt kikapcsoljuk, akkor az elektronnyaláb nem képes megmaradni a toroidban, hanem az ábra síkjára merőleges irányú szisztematikus mozgással (drift) elhagyja azt.   a) Mutasd meg, hogy az elektronok sugárirányban csak véges mértékben térnek el a bebocsátási helyhez tartozó sugártól!   b) Határozd meg a drift-sebesség irányát!   Megjegyzés: Az elektronnyaláb széttartásának szögét elhanyagolhatjuk. Használjuk fel az energia- és a perdületmegmaradás törvényét!   Adatok: ${\displaystyle \begin{array}{c}\hfill {\displaystyle e/m=1\mathrm{,}76\cdot {10}^{11}\text{ C/kg}\mathrm{,}}\hfill \\ \hfill {\displaystyle V_0=3\text{ kV}\mathrm{,}}\hfill \\ \hfill {\displaystyle R=50\text{ mm}\mathrm{.}}\hfill \end{array}}$ Megoldás.   1. A $V_0$ gyorsítófeszültség hatására az $e$ töltésű, $m$ tömegű elektronok $v_0$ sebességre tesznek szert. Ennek a sebességnek a nagyságát a munkatételből kaphatjuk meg: $\begin{array}{c}{\displaystyle \frac{m}{2}{v}_0^2=e\cdot V_0\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle v_0=\sqrt[]{\frac{2\cdot e\cdot V_0}{m}}=3\mathrm{,}25\cdot {10}^7\text{ m/s}\mathrm{.}}\end{array}$ (Ez a sebesség sokkal kisebb, mint a fénysebesség, jogosan számoltunk tehát a klasszikus mechanika energia-képletével. Relativisztikus hatásokat, például a tömegnövekedést csak sokkal nagyobb gyorsítófeszültségek esetén kellene figyelembe vennünk.) A $v_0$ sebességgel $R$ sugarú körpályán keringő elektron mozgásegyenlete: $\begin{array}{c}{\displaystyle \frac{m\cdot v_0^2}{R}=e\cdot v_0\cdot B_1\mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle B_1=\frac{v_0}{R}\cdot \frac{m}{e}=3\mathrm{,}69\cdot {10}^{-3}{\text{ Vs/m}}^2\mathrm{.}}\end{array}$ 2. A mágneses térben körpályán mozgó elektronok szögsebessége a fenti képlet szerint $\begin{array}{c}{\displaystyle {\omega }_1=\frac{v_0}{R}=\frac{e}{m}\cdot B_1\mathrm{.}}\end{array}$ Bontsuk fel a $P$ pontból majdnem párhuzamosan induló elektronok sebességét egy $\text{<span style="font-weight: bold;">B</span>}$-vel párhuzamos ${\text{<span style="font-weight: bold;">v</span>}}_{\parallel }$ és egy arra merőleges ${\text{<span style="font-weight: bold;">v</span>}}_{\perp }$ összetevőre. Az $\text{<span style="font-weight: bold;">F</span>}=-e\left(\text{<span style="font-weight: bold;">v</span>}\times \text{<span style="font-weight: bold;">B</span>}\right)$ Lorentz-erő a sebességnek csak a $\text{<span style="font-weight: bold;">B</span>}$-re merőleges komponensét változtatja meg. $\text{<span style="font-weight: bold;">B</span>}$-re merőleges síkban a mozgás egy $\begin{array}{c}{\displaystyle \omega =\frac{e}{m}\cdot B}\end{array}$ szögsebességű körmozgás, míg a sebesség $\text{<span style="font-weight: bold;">B</span>}$-vel párhuzamos összetevője $\begin{array}{c}{\displaystyle v_{\parallel }\approx v_{\parallel 0}\approx v_0\cdot \text{cos}{\alpha }_0\approx v_0}\end{array}$ valamennyi elektronra azonos nagyságú, ${\omega }_1$ szögsebességgel változó irányú vektor. Ha azt akarjuk elérni, hogy az elektronnyaláb a $\text{<span style="font-weight: bold;">B</span>}$-vel párhuzamos irányban egy negyedkört megtéve fókuszálódjék, vagyis ezalatt valamennyi elektron egy teljes kört tegyen meg a $\text{<span style="font-weight: bold;">B</span>}$-re merőleges irányban, akkor az $\omega =4\cdot {\omega }_1$ feltételt kell biztosítanunk. Ez $\begin{array}{c}{\displaystyle B=4B_1=1\mathrm{,}48\cdot {10}^{-2}{\text{ Vs/m}}^2}\end{array}$ esetén teljesül. 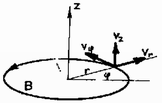3. A toroid belsejében a mágneses erővonalak kör alakúak, a körök középpontja a toroid tekercs szimmetriatengelyére ($z$ tengelyre) esik. A feladat szimmetriája azt sugallja, hogy célszerű a $z$-tengelyre merőleges síkban $r$ és $\phi$ polárkoordinátákat használnunk (3. ábra), s az előforduló vektorokat (sebesség, mágneses indukció, Lorentz-erő) is ilyen irányú összetevőkre felbontanunk.     3. ábra   Mivel az elektronnyaláb széttartása kicsiny, elegendő egyetlen elektron pályáját vizsgálnunk, egy olyanét, amelyik $R$ sugárnál $v_0$ kezdősebességgel érintő irányban lép be a tekercsbe. Állandó mágneses térben a mozgási energia megmaradó mennyiség: $\begin{array}{c}{\displaystyle E=\frac{m}{2}\left(v_r^2+v_{\phi }^2+v_z^2\right)=\frac{m}{2}\cdot v_0^2\mathrm{.}}\end{array}$ Az is igaz továbbá, hogy a Lorentz-erőnek nincsen $\phi$ irányú összetevője (hiszen merőleges $\text{<span style="font-weight: bold;">B</span>}$-re), s emiatt forgatónyomatéka sincsen a $z$ tengelyre vonatkoztatva. Következésképpen az elektronnak a $z$ tengely körüli perdülete (impulzusnyomatéka) időben állandó, megmaradó mennyiség: $\begin{array}{c}{\displaystyle m\cdot v_{\phi }\cdot r=m\cdot v_0\cdot R\mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle v_{\phi }=v_0\cdot \frac{R}{r}\mathrm{.}}\end{array}$ Írjuk fel még az elektron $z$ tengelyirányú mozgásegyenletét! Mivel a Lorentz-erő megfelelő komponense: $\begin{array}{c}{\displaystyle F_z=-eB{v}_r}\end{array}$ (a negatív előjel az elektron negatív töltésére utal), a mozgásegyenlet: $\begin{array}{c}{\displaystyle \frac{\Delta v_z}{\Delta t}=-\frac{e}{m}\cdot B\cdot \frac{\Delta r}{\Delta t}\mathrm{.}}\end{array}$ Mivel $B$ időben állandó, a fenti egyenlet azt fejezi ki, hogy $v_z$ megváltozása pillanatról pillanatra arányos az $r$ koordináta megváltozásával, s ez nem csak kicsiny $\Delta t$, hanem véges nagyságú időtartamokra is igaz. Figyelembe véve, hogy kezdetben $v_z\left(t=0\right)=0$ és $r\left(t=0\right)=R$, később fenn kell álljon, hogy $\begin{array}{c}{\displaystyle v_z=-\frac{e}{m}\cdot B\cdot \left(r-R\right)\mathrm{.}}\end{array}$ Vizsgáljuk meg, milyen határok között mozoghatnak az elektronok sugárirányban! Az $r$ irányú mozgásban a fordulópontokat nyilvánvalóan az jellemzi, hogy $v_r=0$. Az egyik ilyen fordulópont a $P$ pont, itt $r=R$, $v_{\phi }=v_0$ és $v_r=v_z=0$. Kérdés, hogy vannak-e további fordulópontok. Helyettesítsük be $v_{\phi }$ és $v_z$ fentebb kapott kifejezéseit az energiamegmaradást kifejező összefüggésbe, s $v_r$ helyébe írjunk nullát! Azt kapjuk, hogy $\begin{array}{c}{\displaystyle {\left(\frac{R}{r}\right)}^2+A^2\cdot {\left(\frac{r}{R}-1\right)}^2=\mathrm{1,}}\end{array}$ ahol $A=\frac{e}{m}\cdot \frac{R}{v_0}\cdot B=$ állandó. A fenti egyenlet gyökei megadják azokat az $r$ értékeket, ahol az elektron sugárirányú sebessége előjelet vált, vagyis a sugárirányú mozgás visszafordul. Az egyik ilyen hely a már ismert: $r=R$. Ábrázoljuk a fenti egyenlet bal oldalát az $x=r/R$ változó függvényében (4. ábra), s nézzük meg, hogy hol vesz fel ez a függvény 1-es értéket! Az ábráról leolvashatjuk, hogy $r=R$ mellett még egy ilyen hely (még egy sugár) létezik: $r=r_{\text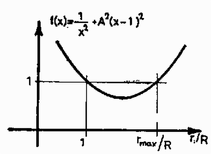{max}}>R$.     4. ábra   Az elektron tehát sugárirányban két véges érték között mozog, ilyen irányban nem léphet ki a tekercsből. (Természetesen feltételeztük, hogy $r_{\text{max}}$ még a tekercs belső pontjára utal.) Mivel a mozgás során mindvégig $r\geqq R$, ebből $v_z\leqq 0$ következik, tehát a driftmozgás a negatív $z$ tengely irányába indul meg.   3. feladat. Ha egy végtelen $LC$-láncban (5. ábra) szinuszos hullámok terjednek, két egymást követő kondenzátor váltófeszültségének fázisa $\phi$-vel különbözik egymástól. 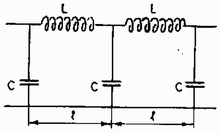    5. ábra   a) Határozd meg, hogyan függ $\phi$ az $\omega$ körfrekvenciától, $L$-től és $C$-től?   b) Határozd meg a hullámok terjedési sebességét, ha az egyes cellák hossza $l$!   c) Állapítsd meg, milyen feltételek esetén igaz, hogy a hullámok terjedési sebessége csak kis mértékben függ $\omega$-tól, és határozd meg ebben az esetben a sebességet!   d) Javasolj olyan egyszerű mechanikai modellt, amely analóg a fenti áramkörrel, és vezess le olyan egyenleteket, amelyek igazolják a modell érvényességét!   Kifejezések: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{cos}\alpha -\text{cos}\beta }& {\displaystyle =-2\cdot \text{sin}\left(\frac{\alpha +\beta }{2}\right)\cdot \text{sin}\left(\frac{\alpha -\beta }{2}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}\alpha -\text{sin}\beta }& {\displaystyle =2\cdot \text{cos}\left(\frac{\alpha +\beta }{2}\right)\cdot \text{sin}\left(\frac{\alpha -\beta }{2}\right)\mathrm{.}}\hfill \end{array}}$ Megoldás.   a) Válasszunk ki önkényesen egy "kezdőpontot'' a lánc mentén, s jelöljük az innen számított $n$-edik kondenzátor töltését $Q_n$-nel, feszültségét $U_n$-nel, az $n$-edik tekercsen átfolyó áramot pedig $I_n$-nel (6. ábra). 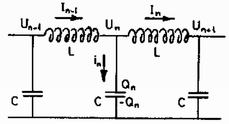    6. ábra   A kondenzátor töltése: $\begin{array}{c}{\displaystyle Q_n=C{U}_n\mathrm{,}}\end{array}$ a kondenzátor "feltöltődési árama'' pedig $\begin{array}{c}{\displaystyle i_n=\frac{\Delta Q_n}{\Delta t}=C\frac{\Delta U_n}{\Delta t}\mathrm{.}}\end{array}$ (1) A csomóponti törvény értelmében $\begin{array}{c}{\displaystyle I_{n-1}-I_n=i_n\mathrm{.}}\end{array}$ Az $n$-edik tekercsben indukált feszültség meg kell egyezzék a végpontjain mérhető feszültségek különbségével: $\begin{array}{c}{\displaystyle -L\cdot \frac{\Delta I_n}{\Delta t}=U_{n+1}-U_n\mathrm{,}}\end{array}$ s ugyanezt felírhatjuk az ($n-1$)-edik tekercsre is $\begin{array}{c}{\displaystyle -L\frac{\Delta I_{n-1}}{\Delta t}=U_n-U_{n-1}\mathrm{.}}\end{array}$ A fenti két egyenletet egymásból kivonva és a csomóponti törvény egyenletébe helyettesítve $\begin{array}{c}{\displaystyle L\frac{\Delta i_n}{\Delta t}=U_{n+1}+U_{n-1}-2\cdot U_n}\end{array}$ (2) adódik. Az (1) és (2) egyenletek (melyek az $U_n\left(t\right)$ és $i_n\left(t\right)$ függvényekre vonatkozó differenciálegyenletek) megoldása megadná az $LC$-lánc feszültség- és áramviszonyainak legáltalánosabb leírását. Ezt az általános megoldást azonban ‐ szerencsére ‐ nem kell megkeresnünk, hiszen a feladat szövege megadja, hogy a láncon egy szinuszos hullám fut végig, cellánként $\phi$ fáziskülönbséggel. Válasszuk a kezdőpontként kijelölt $n=0$ jelzésű kondenzátor váltófeszültségének fázisát $t=0$ pillanatban nullának, s jelöljük a hullám amplitúdóját $A$-val, akkor $\begin{array}{c}{\displaystyle U_n\left(t\right)=A\cdot \text{sin}\left(\omega t+n\phi \right)\mathrm{.}}\end{array}$ (3) Ezt a függvényt (1)-be helyettesítve a töltőáramra $\begin{array}{c}{\displaystyle i_n\left(t\right)=A\cdot C\cdot \omega \text{cos}\left(\omega t+n\phi \right)\mathrm{,}}\end{array}$ a megváltozására pedig $\begin{array}{c}{\displaystyle L\frac{\Delta i_n}{\Delta t}=-A\cdot L\cdot C\cdot {\omega }^2\cdot \text{sin}\left(\omega t+n\phi \right)}\end{array}$ (4) adódik. (A fentiek számításánál kihasználtuk, hogy az $f\left(x\right)=\text{sin}x$ függvény "változási sebessége'' $\text{cos}x$, a $\text{cos}x$ függvényé pedig $-\text{sin}x$.)   Helyettesítsük be (3)-at és (4)-et a (2) egyenletbe: $\begin{array}{c}{\displaystyle -LC{\omega }^2\cdot \text{sin}\left(\omega t+n\phi \right)=\text{sin}\left(\omega t+n\phi +\phi \right)+\text{sin}\left(\omega t+n\phi -\phi \right)-2\cdot \text{sin}\left(\omega t+n\phi \right)\mathrm{,}}\end{array}$ és alkalmazzuk a jobb oldal első két tagjára a $\begin{array}{c}{\displaystyle \text{sin}\alpha +\text{sin}\beta =2\cdot \text{sin}\left(\frac{\alpha +\beta }{2}\right)\cdot \text{cos}\left(\frac{\alpha +\beta }{2}\right)}\end{array}$ azonosságot! A közös $\text{sin}\left(\omega t+n\phi \right)$ tényezővel egyszerűsíthetünk (ezáltal az időfüggés eltűnik az egyenletből, ami azt mutatja, hogy az minden időpillanatban kielégíthető, tehát a megadott "próbamegoldás'' megfelelő), s csupán a $\phi$ fáziskülönbség és az $\omega$ körfrekvencia között kapunk megszorítást: $\begin{array}{c}{\displaystyle -LC{\omega }^2=2\text{cos}\phi -\mathrm{2,}}\end{array}$ ami némi átalakítással $\begin{array}{c}{\displaystyle \frac{\omega }{2{\omega }_0}=\text{sin}\frac{\phi }{2}}\end{array}$ alakra hozható, ahol ${\omega }_0=1/\sqrt[]{LC}$ a rezgőkörökre jellemző Thomson-féle körfrekvenciát jelöli. 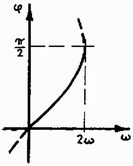    7. ábra   A 7. ábrán felrajzoltuk a keresett függvénykapcsolatot. Látható, hogy az $\omega \leqq 2{\omega }_0$ feltételnek teljesülnie kell; a $2/\sqrt[]{LC}$ értéknél nagyobb körfrekvenciájú jelek nem képesek csillapítás nélkül terjedni a láncban.   b) A hullám fázisa egy adott helyen $t_0=\phi /\omega$ idő alatt változik annyit, amennyi két szomszédos kondenzátor között a fáziskülönbség. Ennyi idő alatt a $v$ sebességgel haladó hullámnak éppen $l$ utat kell megtennie: $l=v{t}_0$. Ezen két összefüggésből a hullám sebességére $\begin{array}{c}{\displaystyle v=\frac{l\cdot \omega }{\phi }=2\cdot l\cdot {\omega }_0\cdot \frac{\text{sin}\phi /2}{\phi }}\end{array}$ (5) adódik, amelyet $\begin{array}{c}{\displaystyle v=\frac{l\cdot \omega }{2\cdot \text{arc}\text{sin}\frac{\omega }{2{\omega }_0}}}\end{array}$ (6) alakba is írhatunk.   c) A (6) formula azt mutatja, hogy az $LC$-láncban terjedő hullámok sebessége (az azonos fázisú pontok terjedési sebessége, tehát a "fázissebesség'') általában függ a körfrekvenciától. (Ez a jelenség hasonló ahhoz, hogy az anyagok (üveg, víz stb.) törésmutatója függ a fény frekvenciájától (színétől), s emiatt a különböző frekvenciájú monokromatikus fénykomponensek különböző sebességgel haladnak át a közegeken.) Ha viszont $\omega \ll {\omega }_0$, akkor a $\text{sin}x\approx x$ és $\text{arc}\text{sin}x\approx x$ közelítő összefüggések miatt fennáll, hogy $\begin{array}{c}{\displaystyle v\approx l{\omega }_0=\frac{l}{\sqrt[]{LC}}=\text{állandó}\mathrm{.}}\end{array}$ Ez a formula csak a kis frekvenciájú, az $L$ és $C$ elemekből építhető rezgőkör rezgésidejénél sokkal nagyobb periódusidejű hullámokra érvényes!   d) A vizsgált $LC$-lánccal analóg (tehát hasonló módon viselkedő) mechanikai rendszer például egy "végtelen hosszú'' lineáris lánc, amely egyforma erősségű rugókkal összekapcsolt azonos tömegű tömegpontokból épül fel. Az analógiát a rendszer mozgásegyenleteinek felírásával és az $LC$-lánc megfelelő egyenleteivel való összehasonlításával igazolhatjuk. Jelöljük az $n$-edik tömegpont elmozdulását $x_n$-nel, az impulzusát pedig $p_n$-nel! (Feltételezzük, hogy a részecskék csak a lánc mentén tudnak elmozdulni.) A rugók megnyúlásából származó eredő erő: $\begin{array}{c}{\displaystyle F_n=k\left(x_{n+1}-x_n\right)-k\left(x_n-x_{n-1}\right)=k\left(x_{n+1}+x_{n-1}-2x_n\right)\mathrm{,}}\end{array}$ tehát a mozgásegyenletek ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\Delta p_n}{\Delta t}=k\left(x_{n+1}+x_{n-1}-2\cdot x_n\right)\mathrm{,}}\hfill & \text{(<mn>7</mn>)}\\ \hfill {\displaystyle p_n=m\cdot \frac{\Delta x_n}{\Delta t}\mathrm{.}}\hfill & \text{(<mn>8</mn>)}\end{array}}$ Hasonlítsuk össze ezeket az egyenleteket (1)-gyel és (2)-vel! Könnyen felismerhetjük az egyenletek alaki azonosságát, ha a változók, illetve a paraméterek között az ${\displaystyle \begin{array}{c}\hfill {\displaystyle x_n\leftrightarrow U_n\mathrm{,}}\hfill \\ \hfill {\displaystyle p_n\leftrightarrow i_n\mathrm{,}}\hfill \\ \hfill {\displaystyle m\leftrightarrow C\mathrm{,}}\hfill \\ \hfill {\displaystyle k\leftrightarrow 1/L}\hfill \end{array}}$ megfeleltetést létesítjük. Az egyenletek alaki azonossága lehetőséget nyújt arra, hogy az $LC$-láncnál talált matematikai megoldást a megfelelő átjelölések után az analóg mechanikai rendszerben terjedő hullámok leírására is felhasználhatjuk. Kiszámíthatjuk például az $\omega$ körfrekvenciájú rugalmas hullámok terjedési sebességét, s leolvashatjuk, hogy ez a sebesség általában frekvenciafüggő, csupán alacsony frekvenciájú határesetben (amikor a hullámhossz sokkal nagyobb, mint a részecskék, az "atomok'' közötti távolság) válik állandóvá. Az analógia segítségével meghatározhatjuk, hogy mi a kapcsolat a longitudinális hullámok terjedési sebessége, valamint $m$, $k$ és $l$ között; ez utóbbiak kapcsolatba hozhatók a modellezni kívánt anyag sűrűségével és Young-moduluszával. Természetesen az itt leírt mechanikai modellen kívül sok más mechanikai rendszer kapcsolatba hozható a vizsgált $LC$-lánccal (például torziós rugókkal összekapcsolt korongok végtelen lánca, vagy transzverzális rezgésekre képes tömegpontok lineáris lánca), sőt még egy adott modell esetén is többféle módon "oszthatjuk ki a szerepeket'', különbözőképpen feleltethetjük meg egymásnak az elektromos és a mechanikai mennyiségeket.   Kísérleti feladat   Határozd meg egy prizma $n_p$ és egy folyadék $n_f$ törésmutatóját! (A diszperzió elhanyagolható.)   a) Egyetlen prizma felhasználásával határozd meg a prizma $n_p$ törésmutatóját kétféleképpen, két elvileg különböző módszer alkalmazásával! Illusztráld a megoldás elvét pontos ábrákkal és a szükséges matematikai összefüggések levezetésével számítsd ki a törésmutatót!   Eszközök: egy prizma ${30}^{\circ }$-os, ${60}^{\circ }$-os és ${90}^{\circ }$-os szögekkel; milliméterpapírok, vonalzó, papírok, kör alakú asztal és ceruza.   b) Két egyforma prizma felhasználásával határozd meg egy adott folyadék $n_f$ törésmutatóját, melyre fennáll, hogy $n_f<n_p$. Illusztráld a megoldás elvét pontos ábrákkal és a szükséges matematikai összefüggések levezetésével számítsd ki a törésmutatót!   Eszközök: két prizma ${30}^{\circ }$-os, ${60}^{\circ }$-os és ${90}^{\circ }$-os szögekkel; milliméterpapírok, vonalzó, papírok, kör alakú asztal, ceruza és egy üvegedényben folyadék.   Megjegyzések:   1. A prizma opálos oldalára szabad ceruzával jelzést rajzolni.   2. A mellékelt lámpát szükség esetén felhasználhatod.   Trigonometriai összefüggés: $\begin{array}{c}{\displaystyle \text{sin}\left(\alpha \pm \beta \right)=\text{sin}\alpha \cdot \text{cos}\beta \pm \text{cos}\alpha \cdot \text{sin}\beta \mathrm{.}}\end{array}$   Megoldás. a) A prizma törésmutatójának meghatározása. 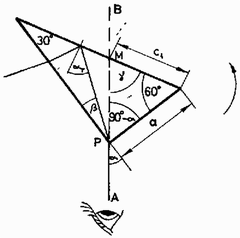    8. ábra   Első módszer. Húzzunk egy fehér papírlapon egy egyenes vonalat ($A$‐$B$), s legyen ez a "látóvonalunk'' (8. ábra). Helyezzük a prizmát a vízszintes papírlapra oly módon, hogy a derékszögű éle a felénk eső oldalra kerüljön, s a $P$ pont illeszkedjék az $A$‐$B$ egyenesre! Forgassuk ezek után a prizmát a nyíllal jelzett irányban mindaddig, míg a teljes visszaverődés sötét határvonala ‐ melyet a prizma rövidebb lapján figyelhetünk meg ‐ egybe nem esik a ${90}^{\circ }$-os éllel. Jelöljük meg ebben a helyzetben a prizma felső, opálos lapján ceruzával az $M$ pontot, majd mérjük meg vonalzóval az ábrán $c_1$-gyel jelölt távolságot! Mérjük meg továbbá a prizma legrövidebb lapjának $a$ oldalélét! A következő összefüggések érvényesek: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}{\alpha }_T=1/n_p\mathrm{,}}\hfill & \text{(<mn>9</mn>)}\\ \hfill {\displaystyle \frac{\text{sin}\alpha }{\text{sin}\beta }=n_p\mathrm{,}}\hfill & \text{(<mn>10</mn>)}\\ \hfill {\displaystyle \beta ={60}^{\circ }-{\alpha }_T\mathrm{,}}\hfill & \text{(<mn>11</mn>)}\\ \hfill {\displaystyle \gamma ={30}^{\circ }+\alpha \mathrm{,}}\hfill & \text{(<mn>12</mn>)}\\ \hfill {\displaystyle \frac{\text{sin}\gamma }{\text{sin}\left({90}^{\circ }-\alpha \right)}=\frac{a}{c_1}\mathrm{.}}\hfill & \text{(<mn>13</mn>)}\end{array}}$ Az utóbbi egyenletből (12) és az addíciós formula felhasználásával $\begin{array}{c}{\displaystyle \frac{a}{c_1}\text{cos}\alpha =\text{sin}\left({30}^{\circ }+\alpha \right)=\frac{1}{2}\text{cos}\alpha +\frac{\sqrt[]{3}}{2}\text{sin}\alpha }\end{array}$ adódik, ahonnan $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{2a-c_1}{2\cdot \sqrt[]{a^2-a\cdot c_1+c_1^2}}\mathrm{.}}\end{array}$ A versenyzők olyan prizmákat kaptak, melyekre $a$ és $c_1$ a kb. 1 mm-es mérési hibahatáron belül egyenlő nagynak adódott, vagyis a kiszámítható $\alpha$ szögre $\text{sin}\alpha =1/2$. Másrészt a (9), (10) és (11) egyenletekből az következik, hogy $\begin{array}{c}{\displaystyle \text{sin}\alpha =n_p\cdot \text{sin}\left({60}^{\circ }-{\alpha }_T\right)=\frac{n_p}{2}\left(\sqrt[]{3}\text{cos}{\alpha }_T-\text{sin}{\alpha }_T\right)\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{1}{2}\left(\sqrt[]{3}\cdot \sqrt[]{n_p^2-1}-1\right)\mathrm{,}}\end{array}$ végül $\begin{array}{c}{\displaystyle n_p=\sqrt[]{\frac{1}{3}{\left(2\cdot \text{sin}\alpha +1\right)}^2+1}\mathrm{.}}\end{array}$ Behelyettesítve $\text{sin}\alpha$ fentebb számított értékét, a prizma törésmutatójára $\begin{array}{c}{\displaystyle n_p=1\mathrm{,}53}\end{array}$ adódik.   Második módszer. Helyezzünk egy fehér papírlapot az asztalra és állítsuk mellé a prizmát oly módon, hogy az a ${30}^{\circ }$-os szöggel szemközti lapján feküdjön és a 9. ábrán látható $C$ ponton átmenő, az ábra síkjára merőleges éle illeszkedjék a papírlap $A$ jelű széléhez. 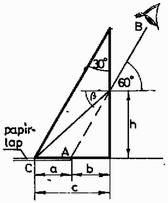    9. ábra   Nézzünk a prizmára ferdén fölülről úgy, hogy a "látóvonalunk'' éppen súrolja a prizmának a ${90}^{\circ }$-os szöggel szemközti oldalát, az "átfogóját''. Toljuk ezek után a prizmát óvatosan a papírlapra mindaddig, míg a prizma $C$ élének képe egy vonalba nem kerül a papírlap $A$ élének prizmán kívül eső részével; a 9. ábra éppen ezt a helyzetet mutatja. Vigyázzunk arra, hogy a szemünk ne mozduljon el a prizma mozgatása közben, vagyis továbbra is a vízszinteshez képest ${60}^{\circ }$-os szögben látszódjék a papírlap széle. Mérjük meg vonalzóval az ábrán $b$-vel és $c$-vel jelölt távolságokat, és vegyük figyelembe, hogy a következő összefüggések érvényesek: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{tg}\beta =h/c\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{tg}{60}^{\circ }=\sqrt[]{3}=h/b\mathrm{,}}\hfill \end{array}}$ ahonnan $\begin{array}{c}{\displaystyle b\sqrt[]{3}=\frac{c\cdot \text{sin}\beta }{\sqrt[]{1-\text{sin}{}^2\beta }}\mathrm{.}}\end{array}$ Másrészt a törési törvényből $\begin{array}{c}{\displaystyle \text{sin}\beta =\text{sin}{60}^{\circ }\cdot \frac{1}{n_p}\mathrm{,}}\end{array}$ melyet az előbbi egyenletbe helyettesítve és $n_p$-t kifejezve $\begin{array}{c}{\displaystyle n_p=\frac{1}{2}\sqrt[]{{\left(\frac{c}{b}\right)}^2+3}}\end{array}$ adódik. A rendelkezésre álló prizmán a távolságmérések eredménye kb. 0,5‐1 mm pontossággal: $c=29$ mm, $b=11\mathrm{,}5$ mm, s ezekből kiszámítható volt, hogy $n_p=1\mathrm{,}53$. Mindkét módszernél a távolságmérés hibája szabta meg a törésmutató mérési hibáját. A bírálók az $1\mathrm{,}49$ és $1\mathrm{,}57$ közé eső eredményeket tekintették elfogadhatónak. Az itt ismertetett két módszer mellett természetesen más, azoktól elvben különböző módszerrel is meg lehet határozni az üveg törésmutatóját. Ha például egy meghatározott pontszerű tárgyat nézünk a prizmán keresztül, s a prizmát lassan elforgatjuk, a tárgy képe elmozdul. Annál a helyzetnél, melynél a sugármenet szimmetrikus a prizma törőszögének szögfelezőjére, a tárgy képe (kicsiny elforgatások esetén) mozdulatlan marad. Ennek az a magyarázata, hogy a szimmetrikus sugármenethez tartozik a legkisebb eltérülési szög. Távolságok mérésével meghatározhatjuk ezt a minimális eltérülési szöget, ${\delta }_{\text{min}}$-t, s könnyen levezethetjük, hogy a prizma törésmutatója és $\phi$ törőszöge, valamint ${\delta }_{\text{min}}$ között fennáll: $\begin{array}{c}{\displaystyle n_p=\text{sin}\left(\frac{\phi +{\delta }_{\text{min}}}{2}\right)\text{sin}\frac{\phi }{2}\mathrm{.}}\end{array}$ Ez az eljárás azonban sokkal pontatlanabbul adja meg $n_p$ értékét, mint a korábbiak.   b) A folyadék törésmutatójának meghatározása két prizma segítségével. 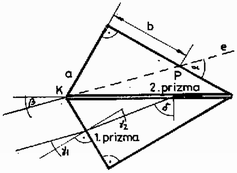    10. ábra   A mérést célszerű a teljes visszaverődés jelenségére alapozni. Cseppentsünk egy kevés folyadékot az egyik prizma "átfogójára'' (vagyis a ${90}^{\circ }$-os szöggel szemközti lapjára), majd szorítsuk hozzá a másik prizmát a 10. ábrán látható módon. A két üveg között egy vékony folyadékfilm alakul ki, s mivel a vizsgálandó folyadék törésmutatója kisebb, mint az üvegé, bizonyos irányú fénysugaraknál teljes visszaverődés játszódik le. Az 1. prizma rövidebb oldalára nézve ezt oly módon érzékeljük, hogy bizonyos irányokból sok fény jut a szemünkbe (ha a 2. prizmából a folyadékhártyán keresztül tud jutni a fény), más irányokból viszont csak kevés fényt kapunk, annyit, amennyi az 1. prizmán áthaladva eljut a szemünkig. Emiatt az 1. prizma rövid oldalán egy éles határvonallal elválasztott sötétebb és világosabb részt látunk. A határvonal helyzetét a 10. ábrán látható ${\gamma }_1$ szög jellemzi, amely ${\gamma }_2$-n keresztül kapcsolatba hozható a teljes visszaverődés $\delta$ határszögével: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\text{sin}{\gamma }_1}{\text{sin}{\gamma }_2}=n_p\mathrm{,}}\hfill & \text{(<mn>14</mn>)}\\ \hfill {\displaystyle \delta ={60}^{\circ }+{\gamma }_2\mathrm{,}}\hfill & \text{(<mn>15</mn>)}\end{array}}$ valamint $\begin{array}{c}{\displaystyle \text{sin}\delta =\frac{n_f}{n_p}\mathrm{.}}\end{array}$ (16) A fenti egyenletek azt mutatják, hogy ${\gamma }_1$ precíz mérésével némi számolás után meghatározhatjuk a folyadék törésmutatóját. A gyakorlatban ezt a következőképpen tehetjük meg. Az összeérintett prizmákat a folyadékot tartalmazó tálkába helyezzük, s megvárjuk, vagy a prizmák óvatos mozgatásával elősegítjük, hogy kialakuljon a folyadékfilm. Ezután keresünk egy jól megfigyelhető, kis kiterjedésű tárgyat (például egy jól megvilágított falfelület valamelyik jellegzetes pontját), s a tekintetünket arra a pontra meresztve kitűzzük az $e$ "látóvonalat'' (11. ábra). 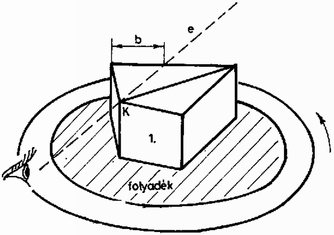    11. ábra   A prizmákat úgy helyezzük el, hogy $e$ áthaladjon a $K$ ponton, továbbá majdnem súrolja a 2. prizma felső vízszintes lapját. Az 1. prizma felénk eső lapján ekkor megfigyelhetjük a teljes visszaverődés határvonalát. Forgassuk most a tálka segítségével a prizmákat a nyíllal jelzett irányban mindaddig, míg a sötét és világos tartományt elválasztó határvonal el nem éri a $K$ pontot, vagyis a prizmák ${60}^{\circ }$-os szöghöz tartozó élét. Ügyeljünk arra, hogy a forgatás közben a $K$ pont rajta maradjon a látóvonalunkon! A kívánt helyzet elérése után ceruzával jelöljük meg azt a $P$ pontot, ahol az $e$ egyenes eléri a 2. prizma hátsó lapjának tetejét, majd vonalzóval mérjük le a 10. ábrán $b$-vel, illetve $a$-val jelölt távolságokat! A mért adatokból kiszámíthatjuk az $\alpha$ szöget: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{a}{b}\mathrm{,}}\end{array}$ majd ebből $\beta =\alpha -{30}^{\circ }$,  ${\gamma }_1={30}^{\circ }-\beta ={60}^{\circ }-\alpha$ ismeretében (14), (15) és (16) segítségével eljutunk a keresett $n_f$ törésmutatóhoz. A versenyzők 1 mm pontossággal $b=1\mathrm{,}9$ cm és $a=2\mathrm{,}8$ cm értékeket mérhettek, s ebből $n_f=1\mathrm{,}33$ számított érték adódott. (Az ismeretlen folyadék víz volt.) A bírálók $1\mathrm{,}30$ és $1\mathrm{,}38$ közötti végeredményt fogadták el helyes mérési eredménynek. Az itt ismertetett eljárás képezi az úgynevezett Abbe-féle refraktométer elvi alapját. Ennek a műszernek a segítségével ‐ ha megfelelő hőmérséklet-stabilizálást biztosítunk ‐ akár 4 tizedesjegy pontossággal is meg lehet határozni a folyadékok törésmutatóját, de már az egyszerűbb változata is alkalmas arra, hogy a törésmutató mérésén keresztül különböző oldatok (például borok) cukortartalmát, vagy akkumulátor-folyadék savkoncentrációját határozhassuk meg.