,,A csoda, a matematika nyelvének alkalmas volta a fizika törvényeinek megfogalmazására. varázslatos adomány, amelyet nem értünk és nem is érdemlünk meg.''
Wigner Jenő

Bevezetés^{${}^{*}$}

v=5i  m/s egyenlőséget bizonyára őrültségnek tartották volna, a kvantumelmélet (más néven hullámmechanika) megszületése óta azonban már nem nevetik ki azt, aki ilyen ,,vad'' dolgokat állít. A képzetes sebesség fizikai jelentésének tárgyalására nem térhetünk ki, elégedjék meg az Olvasó azzal, hogy nem feltétlenül irreális, fizikailag értelmetlen ez a fogalom.

 

Többértékű megoldások

 

Egy $H$ magasságú toronyból $t=0$ pillanatban $v_0$ kezdősebességgel a vízszinteshez képest $\alpha$ szögben elhajítunk egy testet. Milyen messze és mennyi idő múlva ér földet (1.  ábra)?

 

 

1. ábra

 

A mozgásegyenletek általános alakja:

$\begin{array}{c}{\displaystyle x=v_0\cdot t\cdot \text{cos}\alpha \mathrm{,}}\end{array}$

(3)

$\begin{array}{c}{\displaystyle y=-\frac{\text{g}}{2}{t}^2+v_0\cdot t\cdot \text{sin}\alpha +H\mathrm{.}}\end{array}$

(4)

A földet érés azon $t=T$ pillanatban következik be, amikor $y=0$ teljesül, vagyis

$\begin{array}{c}{\displaystyle -\frac{\text{g}}{2}{T}^2-v_0\cdot T\cdot \text{sin}\alpha +H=0.}\end{array}$

(5)

Ennek a másodfokú egyenletnek két megoldása van:

$\begin{array}{c}{\displaystyle T_{\mathrm{1,2}}=\frac{v_0}{\text{g}}\text{sin}\alpha \pm \sqrt[]{\frac{v_0^2\text{sin}{}^2\alpha }{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>g</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}}+\frac{2H}{\text{g}}}\mathrm{,}}\end{array}$

s az ezekhez tartozó vízszintes irányú elmozdulások:

$\begin{array}{c}{\displaystyle d_{\mathrm{1,2}}=\frac{v_0^2\cdot \text{sin}\alpha \cdot \text{cos}\alpha }{\text{g}}\cdot \left(1\pm \sqrt[]{\frac{2\text{g}H}{v_0^2\text{sin}{}^2\alpha }}\right)\mathrm{.}}\end{array}$

Hogyan lehetséges az, hogy az esési időre, illetve a hajítási távolságra kétféle megoldást kaptunk? Az eldobott tárgy ‐ hacsak nem törik ketté, ‐ nem érhet két különböző helyen földet! Melyik a jó megoldás, s a másik, ha nem jelent semmit, akkor hogyan került a képletünkbe?
A két megoldás közül nyilván a pozitív négyzetgyökhöz tartozó felel meg az 1. ábrán látható $A$ pont adatainak. A másik gyökpár negatív: $T_2<0$ és $d_2<0$; ezeknek a számoknak semmi köze nincsen a keresett $A$ pont jellemzőihez. Ennek ellenére nem állítjuk, hogy $d_2$ és $T_2$ semmiféle fizikai jelentéssel nem rendelkező hamis gyökök, hiszen az értelmük elég könnyen kideríthető. A megoldásunk ugyanis arra ,,épült'', hogy a ferde hajítást végző test pályáján olyan pontot kerestünk, amely a talajszinten található, vagyis amelynek az $y$ koordinátája nulla. Az általunk vizsgált mozgásnál egyetlen ilyen tulajdonságú pont létezik, az $A$ pont. Ha viszont úgy képzeljük el a mozgást hogy az nem a $t=0$ pillanatban kezdődött, hanem már korábban, méghozzá oly módon, hogy $t=0$-kor éppen $y=H$ magasságba jutott el a test és a sebessége pontosan azt az a szöget zárta be a vízszintessel, amelyiket előre megadtunk, akkor a (3) és (4) egyenletek továbbra is érvényesek, s az (5) feltételnek most már nem csupán az $A$, hanem a $B$ pont is eleget tesz.
A másodfokú egyenlet másik, az eredeti feladat szempontjából érdektelen gyöke tehát egy újabb ‐ az eredetivel rokon, de attól mégis különböző kérdésre ad választ: egy $H$ magasságú torony tövétől milyen távolról és mikor kell eldobjunk egy testet, ha azt akarjuk, hogy egy megfelelő pillanatban (mondjuk $t=0$-kor) éppen a torony tetejénél legyen, és a sebessége egy megadott irányba mutasson.
Ez a példa tehát arra tanít bennünket, hogy egy fizikai probléma helyesen megfogalmazott egyenleteinek gondos matematikai megoldása, illetve a megoldás diszkussziója néha olyan, a kitűzöttnél általánosabb probléma megoldását is a kezünkbe adja, melyet eredetileg esetleg fel se vetettünk, meg se fogalmaztunk. Ilyen helyzetekben olyan érzésünk támadhat, hogy egyenleteinkből több ,,fizika'' jön ki, mint amennyit a feladat megfogalmazásakor, az egyenletek felállításakor ,,beleraktunk'', tehát a természet viselkedése, a megfigyelhető jelenségek szabályszerűsége pusztán matematikai megfontolásokkal ,,kitalálható''. Ez így nyilván nem igaz, inkább arról van szó, hogy az általunk felírt és alkalmazott fizikai törvények sokkal többet ,,tudnak'', sokkal több fizikai tartalommal rendelkeznek, mint amennyit első ránézésre nekik tulajdonítottunk.

 

Árulkodó képletek

 

Egy fizikai probléma megoldása során adódó végeredmény különböző okok miatt lehet hibás. Elképzelhető, hogy rosszul emlékeztünk az alaptörvények alakjára, vagy kifelejtettünk egy állandót, de az is lehetséges, hogy az egyenletek megoldása során vétünk valahol egy matematikai jellegű hibát. Bármi legyen is a hiba oka, egy rossz képlet sok bajt okozhat (épületek dőlhetnek össze, tv készülékek gyulladhatnak ki, vagy egyetemi felvételi vizsgák eredménye változhat meg egy-egy számolási hiba miatt). Jó lenne valamilyen ellenőrző mechanizmus, vagy a számítógépek önműködő hibajelző kódjához hasonló eljárás, amely ‐ ha nem is mindig és minden körülmények között, de legalább bizonyos esetekben ‐ figyelmeztet: Vigyázz, amit számoltál, az biztosan nem lehet jó!
Az egyik leghatékonyabb hibajelzés a dimenziópróba. A fizikai mennyiségek általában nem puszta számok, hanem különféle mértékegységgel, dimenzióval rendelkeznek. Ha egy képlet dimenzióra nem helyes, akkor egészen biztosan hibás kell legyen. Sajnos fordítva nem igaz; ha a mértékegységek rendben vannak, akkor még mindig nagyon sokféle hiba lehet a számolásban.
Egy másik ‐ talán kevésbé ismert ‐ hibakeresési eljárás az, amely a végeredmény, a végképlet matematikai szerkezetének vizsgálatára épül, tehát a megoldás diszkusszióján alapszik. Megvizsgálhatjuk például azt, hogy formulában szereplő adatok, paraméterek milyen értékénél, vagy értékeinél ,,bolondul meg'' a képlet, válik szingulárissá a megoldás. Ha ez a megbolondulás fizikailag reális, tehát ténylegesen megvalósítható, beállítható adatok mellett történik, ilyen esetben válik valamelyik mennyiség végtelen naggyá, vagy éppen komplex számmá, akkor erről bizonyára nem a természet, hanem mi magunk tehetünk, s legjobb lesz, ha rögtön nekilátunk az egész számítás gondosabb megismétléséhez.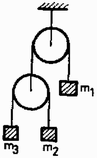

 

 

2. ábra

 

Tekintsük például a 2. ábrán látható csigarendszert, melynél az egyes testek gyorsulását szeretnénk kiszámítani. (A szokásos elhanyagolásokkal élünk: a csigák és a kötelek tömegét, valamint a súrlódást és a légellenállást nem vesszük számításba.) Tegyük fel, hogy az $m_1$ tömegű test gyorsulására ‐ a Newton-egyenletek felírása, bonyolult kényszerfeltételek figyelembe vétele, majd hosszas számolás után ‐ az alábbi összefüggést kapjuk:

$\begin{array}{c}{\displaystyle a_1=\frac{m_1\cdot m_2+m_1\cdot m_3-4m_2\cdot m_3}{m_1\cdot m_2-m_1\cdot m_3+4m_2\cdot m_3}g\mathrm{.}}\end{array}$

(6)

Ez a képlet dimenzióra helyes, ennek ellenére már ránézésre látszik, hogy hibás kell legyen. Miért? A nevezőben pozitív számok összege, illetve különbsége szerepel, s semmi akadálya nincsen annak, hogy történetesen olyan $m_1$, $m_2$ és $m_3$ tömegértékeket válasszunk, amelyeknél a nevező nullává válik (pl. $m_1=6\text{kg}\mathrm{,}{m}_2=1\text{kg és }{m}_3=3\text{ kg})\mathrm{.}$ Mivel ugyanezekkel az adatokkal számolva a számláló egy véges (nullától különböző) érték, a (6) képlet alapján számolt gyorsulás értelmetlenné (,,végtelen naggyá'') válik. Valóban, ha átnézzük a számításunkat, előbb-utóbb rájövünk, hogy a képlet hibás, hiszen a jó eredmény:

$\begin{array}{c}{\displaystyle a_1^{\text{(helyes)}}=\frac{m_1\cdot m_2+m_1\cdot m_3-4\cdot m_2\cdot m_3}{m_1\cdot m_2+m_1\cdot m_3+4\cdot m_2\cdot m_3}g\mathrm{.}}\end{array}$

Ebben a formulában a nevező sohasem válhat nullává, hiszen a tömegek mindegyike pozitív számértékű, tehát az így számolt gyorsulás semmilyen körülmények között nem lesz szinguláris.
Természetesen ez a hibakeresési eljárás sem tökéletes, mindig és minden körülmények között hatásos ,,csodagyógyszer''. Ha például a számolási hiba mindössze annyi, hogy a végképlet elé tévedésből egy 2-s szorzó kerül (fölöslegesen), ezt sem a dimenzió-vizsgálat, sem pedig a szingularitás-próba nem képes kimutatni. Ilyen jellegű hibák felkutatására olyan határesetek megvizsgálása adhat reményt, melyeknél számszerűen tudjuk a végeredményt. (Példánkban ha $m_1$ sokkal nagyobb, mint $m_2$ és $m_3$, akkor az 1 jelű test lényegében szabadon esik, gyorsulása tehát $a_1=g$ kell legyen.)

 

Végtelen ‐ fizikai jelentéssel

 

Az előző pontban leírtak azt sugallják, hogy egy képlet ok nélkül (értsd: fizikailag megvalósítható körülmények között) nem válhat szingulárissá, nem adhat végtelen nagy értéket eredményként. Mint az alábbi példa mutatja, ez azért nem ilyen egyszerű!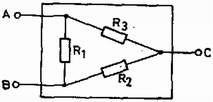

 

 

3. ábra

 

Valaki egy ,,fekete dobozba'' három ellenállást rejtett a 3. ábrán látható kapcsolásban. Hogyan tudnánk meghatározni a doboz kinyitása nélkül az $R_1$, $R_2$ és $R_3$ ellenállásértékeket? Nyilván megtehetjük, hogy egy feszültségmérő és egy árammérő műszerrel rendre megmérjük az $AB$, $BC$ és $AC$ pontok közötti ellenállást, s mondjuk 1 k$\Omega$, 2 k$\Omega$ és 3 k$\Omega$ értékeket kapunk. Ezek után felírhatjuk a sorosan, illetve párhuzamosan kapcsolt ellenállások eredőjét megadó képleteket (tehát lényegében a Kirchhoff-egyenleteket), s így az alábbi összefüggéseket kapjuk:

${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{1}{R_1}+\frac{1}{R_2+R_3}=\frac{1}{1\text{k<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>}}\mathrm{,}}\\ \hfill {\displaystyle \frac{1}{R_2}+\frac{1}{R_1+R_3}=\frac{1}{2\text{k<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>}}\mathrm{,}}\\ \hfill {\displaystyle \frac{1}{R_3}+\frac{1}{R_1+R_2}=\frac{1}{3\text{k<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>}}\mathrm{.}}\end{array}}$

Mivel pontosan annyi ismeretlen mennyiséget szeretnénk meghatározni, ahány egyenletünk van, a feladat matematikai szempontból határozottnak látszik. Az egyenletrendezés során azonban kiderül, hogy nem ilyen egyszerű a helyzet: bizonyos képletekben nullával kellene osztanunk, s ez értelmetlen matematikai művelet (minden valamirevaló számítógép ilyen feladat láttán hibajelzéssel leáll). No, de akkor mekkorák az $R_i$ ellenállások? Egy egyenlet (vagy egyenletrendszer) matematikai szempontból lehet ellentmondásos, tehát megoldhatatlan, de a Természetet leíró egyenletek ezt a luxust ,,nem engedhetik meg maguknak'' ‐ gondolhatjuk, s nem is teljesen alaptalanul. A Természet ugyanis valahogyan biztosan viselkedik, valami mindig történik, s ha a jelenségeket, folyamatokat leíró egyenletek (természetesen valamilyen keretek között) helyesen írják le a valóságot, akkor ennek az egyenletek matematikai szerkezetében, az egyenletek megoldhatóságában is tükröződni kell.
Visszatérve az ellenálláshálózat problémájához, megpróbálkozhatunk azzal, hogy nem a ténylegesen mért 1, 2 és 3 k$\Omega$-os értékekkel, hanem általánosan $R_{AB}$, $R_{BC}$ és $R_{AC}$ paraméterértékekkel oldjuk meg az egyenletrendszerünket, s csak a legvégén helyettesítjük be a konkrét számadatokat. Ezzel persze nem kerülhetjük el, csupán halogathatjuk a nullával való osztás kérdését. Az általános megoldásból kiderül, hogy csupán akkor válik szingulárissá a feladat, ha a mért ellenállások nem tesznek eleget a háromszög egyenlőtlenségnek, vagyis ha nem igaz az, hogy bármelyik kettő összege nagyobb, mint a harmadik érték. Jelen esetben éppen a határon vagyunk $1\text{k<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>+ 2 }\text{k<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>=3 }\text{k<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>}$, ezért éppen megoldhatatlan (pontosabban kiszámíthatatlan) a feladat. Amennyiben a harmadik ellenállásmérés eredménye nem pontosan 3 k$\Omega$-t adott volna, hanem annál egy picivel kevesebbet, mondjuk $\left(3-\epsilon \right)$ k$\Omega$-t, ahol $\epsilon$ egy nagyon kicsi szám, akkor a feladat már megoldható lenne, s azt is látnánk, hogy az $R_3$ ellenállás számított értéke arányos lenne $\frac{1}{\epsilon }$-nal. Mit jelent ez? Mivel végtelen pontos mérés elképzelhetetlen, nyugodtan mondhatjuk, hogy ténylegesen $\left(3-\epsilon \right)$ k$\Omega$ a harmadik mérés eredménye, s ebből az következik, hogy az $R_3$ ellenállás nagyon nagy, a többiekhez viszonyítva ,,végtelen''. Mivel az ellenállás fogalmát a fizikában a feszültség és az áramerősség hányadosaként értelmezhetjük, a végtelen nagy ellenállás nem irreális fogalom, hanem egyszerűen csak azt fejezi ki, hogy a vizsgált ágban nem folyik áram, szakadás található.
Hasonló példákat találhatunk a fizika más területein is; a legkülönbözőbb fizikai mennyiségeknek lehet végtelen nagy az értéke ‐ reális, megvalósítható körülmények között. Így például a szupravezető állapotban levő fémek elektromos vezetőképessége végtelen, a szuperfolyékony héliumnak a viszkozitása nulla, tehát az ennek reciprokával arányos ,,áramlóképessége'' végtelen nagy. Ugyancsak végtelen nagy egy közönséges fém dielektromos állandója, hiszen tetszőleges kicsiny külső elektromos mező hatására számottevő mértékben polarizálódik. Egy párhuzamos határfalú üveglap (planparalel lemez) olyan lencsének tekinthető, melynek végtelen nagy a fókusztávolsága, a Naprendszerből éppen kiszökő űrszonda pályája pedig egy olyan ellipszisnek, amelynek végtelen nagy a nagytengelye. Más kérdés az, hogy az említett példákban a ,,végtelen nagy'' mindig annyit jelent csupán, hogy ,,nagyon nagy'' a vizsgált jelenségkörben szereplő többi mennyiséghez viszonyítva, a ,,végtelen kicsi'', azaz nulla pedig annyit, hogy valami a többi (hozzá hasonló dimenziójú) mennyiséghez képest nagyon kicsi; ennek részletesebb elemzése egy külön előadást igényelne.

---

^{${}^{*}$} Elhangzott a 44. Téli Ifjúsági Fizikai Ankéton.