1. Bizonyítsuk be. hogy három egy pontból induló félegyenes akkor és csak akkor tartalmazhatja egy téglatest három lapátlóját, ha a félegyenesek páronként hegyesszöget zárnak be és ezek összege ${180}^{\circ }\mathrm{.}$

 

1. ábra

 

2. ábra

AB',CD';B'C,D'A;AC,B'D' szembenfekvő élpárok a tégla két-két szembenfekvő lapjának egy-egy átlója ; ezek a lapok egybevágó téglalapok és a téglalap két átlója egyenlő hosszú.
Ekkor egybevágók a következő háromszögek : $AC{D}^{\text{'}}\mathrm{,}CA{B}^{\text{'}}\mathrm{,}{D}^{\text{'}}{B}^{\text{'}}A$ és igy

$\begin{array}{c}{\displaystyle CA{B}^{\text{'}}\sphericalangle =ACD\text{'}\sphericalangle \mathrm{,}{B}^{\text{'}}A{D}^{\text{'}}\sphericalangle =C{D}^{\text{'}}A\sphericalangle \mathrm{.}}\end{array}$

A jobb oldali szögek az $AC{D}^{\text{'}}$ háromszög belső szögei, tehát a három lapátló közti szögek összege :

$\begin{array}{c}{\displaystyle B^{\text{'}}AC\sphericalangle +CA{D}^{\text{'}}\sphericalangle +D^{\text{'}}A{B}^{\text{'}}\sphericalangle =D^{\text{'}}AC\sphericalangle +CA{D}^{\text{'}}\sphericalangle +A{D}^{\text{'}}C\sphericalangle ={180}^{\circ }\mathrm{.}}\end{array}$

Ezzel beláttuk a feladatban szereplő feltételek szükséges voltát.

 

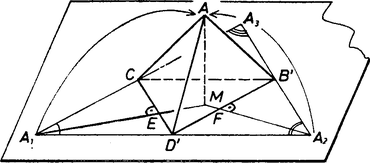3. ábra

 

Teljesüljön az $\alpha \mathrm{,}\beta \mathrm{,}\gamma$ hegyesszögekre az $\alpha +\beta +\gamma ={180}^{\circ }$ összefüggés. Rajzoljunk $A_1{A}_2{A}_3$ háromszöget, amelyiknek ekkorák a szögei. Jelöljük az
$A_2{A}_3\mathrm{,}{A}_3{A}_1\mathrm{,}{A}_1{A}_2$ oldalak felezőpontját rendre $B^{\text{'}}\mathrm{,}C\mathrm{,}{D}^{\text{'}}$-vel (3. ábra). (Így maradunk összhangban az eddigi jelölésekkel.) A $C{A}_1{D}^{\text{'}}$ háromszöget a $C{D}^{\text{'}}$ oldala körül, a $B^{\text{'}}{A}_2{D}^{\text{'}}$ háromszöget pedig a $B^{\text{'}}{D}^{\text{'}}$ oldala körül forgatva az $A_1$ és $A_2$ pontok találkoznak a tér egy $A$ pontjában. Az $A_1$ pont vetülete ugyanis az $A_1$-ből $C{D}^{\text{'}}$-re állított merőlegesen mozog. Ez merőleges $A_2{A}_3$-ra is, tehát az $A_1{A}_2{A}_3$ háromszög magasságvonala. Metszéspontját $C{D}^{\text{'}}$-vel jelöljük $E$-vel. Ez felezi a magasságot. Hasonlóan $A_2$ vetülete a $B^{\text{'}}{D}^{\text{'}}$-re merőleges egyenesen mozog a forgatás során. Ez a háromszög $A_2$-ből húzott magasságvonala, a háromszögbe eső szakaszát a $B^{\text{'}}{D}^{\text{'}}$-vel való $F$ metszéspont felezi.
A két egyenes $M$ metszéspontja a háromszög magasságpontja. Ez a háromszög belsejében van, mert a háromszög hegyesszögű. Az említett felezési tulajdonságok miatt

$\begin{array}{c}{\displaystyle A_{1}E>EM\text{és}{A}_{2}F>FM\mathrm{.}}\end{array}$

Ennek folytán az a kör, amelyiken $A_2$ mozog, az $M$ pontban a háromszög síkjára merőlegesen álló egyenest metszi. A metszéspont legyen $A\mathrm{.}$ Erre

$\begin{array}{c}{\displaystyle A{D}^{\text{'}}=A_1{D}^{\text{'}}=D^{\text{'}}{A}_2\mathrm{,}}\end{array}$

így ugyanebbe a pontba jut a forgatás közben $A_2$ is. Az $A$ pontra teljesülnek az

$\begin{array}{c}{\displaystyle AC=C{A}_1=C{A}_3\text{és}A{B}^{\text{'}}=B^{\text{'}}{A}_2=B^{\text{'}}{A}_3}\end{array}$

egyenlőségek, tehát az $A{B}^{\text{'}}C$ háromszög egybevágó $A_3{B}^{\text{'}}C$-vel. Az $A{B}^{\text{'}}\mathrm{,}AC$ és $A{D}^{\text{'}}$ félegyenesek közti szögek tehát az adott hegyesszögekkel egyenlők, az $A{B}^{\text{'}}C{D}^{\text{'}}$ tetraéder pedig egyenlő oldalú.

 

4. ábra

 

Olyan téglatestet kell még szerkesztenünk, amelyiknek az $A$ csúcsból induló élek lapátlói. Húzzunk $A{B}^{\text{'}}$ felezőpontján át olyan $D^{\text{'}}C$-vel egyenlő és egy irányban párhuzamos $A^{\text{'}}B$ szakaszt, amelyet a pont szintén felez, és hasonlóan $C{D}^{\text{'}}$ felezőpontján át $B^{\text{'}}A$-val egyenlő, párhuzamos és egyirányú $C^{\text{'}}D$ szakaszt, amelyet a pont szintén felez (4. ábra). Ekkor $A{A}^{\text{'}}{B}^{\text{'}}B$ és $C{C}^{\text{'}}{D}^{\text{'}}D$ párhuzamos oldalú és egybevágó téglalapok, mert átlóik egyenlők és felezik egymást, tehát $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ paralelepipedon. Ekkor azonban téglalapok a többi lapjai is, mert

$\begin{array}{c}{\displaystyle BD=B^{\text{'}}{D}^{\text{'}}=AC=A^{\text{'}}{C}^{\text{'}}\text{és}B{C}^{\text{'}}=A{D}^{\text{'}}=C{B}^{\text{'}}=D{A}^{\text{'}}\mathrm{,}}\end{array}$

mivel a tetraéder szemben fekvő élei egyenlők. A paralelepipedon tehát téglatest. Ezzel a feladatot megoldottuk.

 

Megjegyzések. 1. A megoldásból látható, hogy tetszés szerinti $A{B}^{\text{'}}C{D}^{\text{'}}$ tetraéderhez megszerkeszthető az $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ paralelepipedon, a tetraéder ún. bennfoglaló paralelepipedonja. Erre vonatkozóan lényegében azt láttuk be, hogy a bennfoglaló paralelepipedon akkor és csak akkor téglatest, ha a tetraéder egyenlőoldalú. Hozzátehetjük ‐ ez könnyen látható ‐, hogy akkor és csak akkor kocka, ha a tetraéder szabályos.

 

2. Az előző megjegyzésnek és a feladat állításának az összevetéséből azt is kapjuk, hogy az egyenlőoldalú tetraéder élei közti szögek hegyesszögek. Nem igaz viszont a megfelelő állítás a lapok közti szögekre. A fenti megoldásban felhasználtuk, hogy az $M$ magasságpont az $A_1{A}_2{A}_3$ háromszög belsejében van, mert az hegyesszögű. Nem kell azonban a $B^{\text{'}}C{D}^{\text{'}}$ középháromszögben lennie. Ha pl. a $D^{\text{'}}{A}_2{B}^{\text{'}}$ háromszögbe esik (5. ábra), akkor az $A{B}^{\text{'}}{D}^{\text{'}}$ és $B^{\text{'}}C{D}^{\text{'}}$ lapok szöge tompaszög.

 

5. ábra

 

III. megoldás. Fektessünk az $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ téglatest $A$ csúcsán át az $AC$ lapátlóra merőleges síkot (6. ábra). Ennek a téglával az $A{A}^{\text{'}}$ éle közös, a test a sík egyik oldalán fekszik. Ennélfogva az $A{B}^{\text{'}}$ és $A{D}^{\text{'}}$ félegyenesek hegyesszöget zárnak be a síkra merőleges $AC$ félegyenessel. Hasonlóan látható be, hogy az utoljára említett két félegyenes is hegyesszöget zár be.

 

6. ábra

 

 

7. ábra

 

Tükrözzük a téglatestet az $A{A}^{\text{'}}{D}^{\text{'}}D$ és $B{B}^{\text{'}}{C}^{\text{'}}C$ lapok középpontján átmenő tengelyre (7. ábra). Ekkor a $B^{\text{'}}A{D}^{\text{'}}\sphericalangle$ és a $C{D}^{\text{'}}A\sphericalangle$ egymásba megy át, tehát ezek egyenlők. Az $ABCD$ és $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ lapokra merőleges tengelyen át tükrözve kapjuk a $D^{\text{'}}CA\sphericalangle$ és $B^{\text{'}}AC\sphericalangle$ egyenlőségét. Az $A{B}^{\text{'}}\mathrm{,}AC\mathrm{,}A{D}^{\text{'}}$ lapátlók közti szögek tehát az $AC{D}^{\text{'}}$ háromszög belső szögeivel egyenlők, s így összegük ${180}^{\circ }\mathrm{.}$ Ezzel a feltételek szükséges voltát beláttuk.
Legyen most $\alpha \mathrm{,}\beta \mathrm{,}\gamma$ három hegyesszög, amelyek összege ${180}^{\circ }\mathrm{.}$ Rajzoljunk a síkban $\gamma$ szöget bezáró $e$ és $f$ félegyenest, majd egy $\alpha$ nyílásszögű körkúpot $e$ tengellyel és egy $\beta$ nyílásszögűt $f$ tengellyel. Ezek metszik egymást. Legyen ugyanis a kúpok metszésvonala $e$ és $f$ síkjával $g_1\mathrm{,}{h}_1$ és $g_2\mathrm{,}{h}_2\mathrm{,}$ akkor ezek közül kettő, mondjuk $h_1$ és $h_2\mathrm{,}$ egymás meghosszabbítása, mert a szögek összege ${180}^{\circ }$ (8. ábra). A $g_1\mathrm{,}{h}_1$ és $g_2\mathrm{,}{h}_2\mathrm{,}$ félegyenesek közti szögtartomány nyílásszöge $2\alpha \mathrm{,}$ ill. $2\beta \mathrm{.}$ Mivel

$\begin{array}{c}{\displaystyle 2\alpha +2\beta ={360}^{\circ }-2\gamma >{180}^{\circ }\mathrm{,}}\end{array}$

így a két szögtartomány átfedi egymást. Közös részük mindkét kúpban benne van, azok tehát valóban metszik egymást. Egyik metszésvonalukat $g$-vel jelölve, az $e\mathrm{,}f\mathrm{,}g$ félegyenesek közti szögek $\gamma \mathrm{,}\beta$ és $\alpha \mathrm{.}$

 

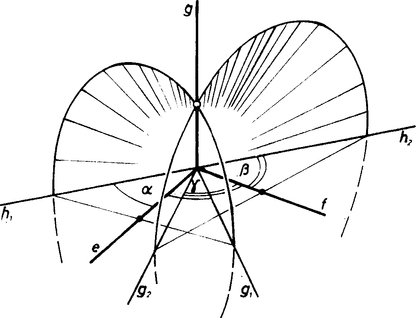8. ábra

 

 

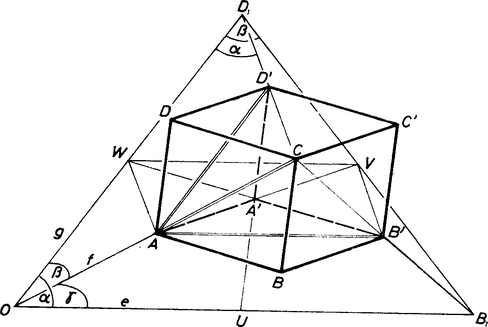9. ábra

 

Jelöljük a félegyenesek közös kezdőpontját $0$-val. Legyen $g$ egy ettől különböző pontja $D_1\mathrm{.}$ Húzzuk meg $D_1$-ből az $O{D}_1$-gyel $e$ és $g$ síkjában $\left(f\mathrm{,}g\right)\sphericalangle \left(=\beta \right)$ és $f$ és $g$ síkjában $\left(e\mathrm{,}g\right)\sphericalangle \left(=\alpha \right)$ szöget bezáró egyenest (9. ábra). Az előbbinek $e$-vel, ill. az utóbbinak $f$-fel való metszéspontja legyen $B_1\mathrm{,}$ ill. $C\mathrm{.}$ Ekkor az $O{B}_1{D}_1$ és a $D_{1}CO$ háromszög egybevágó, mert a közös $O{D}_1=D_{1}O$ oldalukon levő szögek egyenlők. Így $O{B}_1=D_{1}C$ és $B_1{D}_1=CO\mathrm{.}$ Ekkor viszont a $B_{1}OC$ háromszög is egybevágó az előbbiekkel, mert

$\begin{array}{c}{\displaystyle B_{1}OC\sphericalangle =\gamma =O{B}_1{D}_1\sphericalangle \mathrm{,}}\end{array}$

és a megfelelő szögszárakon levő oldalak egyenlők. Így viszont a $C{D}_1{B}_1$ három-szög is egybevágó az előbbiekkel, mert az utolsó egybevágóságból következik, hogy $C{B}_1=O{D}_1$ és így pl. az $O{B}_1{D}_1$ háromszöggel megfelelő oldalaik egyenlők. Az $O{B}_{1}C{D}_1$ tetraéder tehát egyenlőoldalú.
Jelöljük a $CO\mathrm{,}C{B}_1\mathrm{,}C{D}_1\mathrm{,}O{B}_1\mathrm{,}{B}_1{D}_1\mathrm{,}{D}_{1}O$ élek felezőpontját rendre
$A\mathrm{,}{B}^{\text{'}}\mathrm{,}{D}^{\text{'}}\mathrm{,}U\mathrm{,}V\mathrm{,}W$-vel. Ekkor $A\mathrm{,}{B}^{\text{'}}\mathrm{,}V\mathrm{,}W$ egy rombusz csúcsai, mert $A{B}^{\text{'}}$ és $WV$ párhuzamos $O{B}_1$-gyel és fele akkora, miután az $OC{B}_1\mathrm{,}$ ill. $O{D}_1{B}_1$ háromszög középvonala. Így egy síkban vannak és egy paralelogramma csúcsai. Ezen felül $AW$ a $CO{D}_1$ háromszög középvonala, tehát félakkora, mint $C{D}_1\mathrm{,}$ ami meg $O{B}_1$-gyel egyenlő. Így a paralelogramma valóban rombusz, tehát $AV$ és$B^{\text{'}}W$ átlói merőlegesek és felezik egymást. Hasonlóan látható, hogy $AUV{D}^{\text{'}}$ és $B^{\text{'}}{D}^{\text{'}}WU$ is rombusz, így $AV\mathrm{,}{B}^{\text{'}}W$ és $D^{\text{'}}U$ páronként merőlegesek és felezőpontjuk közös; jelöljük ezt $A^{\text{'}}$-vel.
Az $A^{\text{'}}$ pontból az $A{B}^{\text{'}}{D}^{\text{'}}$ háromszög oldalai derékszögben látszanak. Legyen $B\mathrm{,}{C}^{\text{'}}\mathrm{,}$ ill. $D$ az a pont, amire $A{A}^{\text{'}}{B}^{\text{'}}B\mathrm{,}{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}\mathrm{,}$ ill. $A{A}^{\text{'}}{D}^{\text{'}}D$ paralelogramma. Mivel ezek a paralelogrammák téglalapok, az $ABCD{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ paralelepipedon téglatest, Ennek $A{B}^{\text{'}}\mathrm{,}AC\mathrm{,}A{D}^{\text{'}}$ lapátlói rendre $O{B}_1\mathrm{,}OC\mathrm{,}O{D}_1$-gyel párhuzamosak, így a köztük levő szögek az adott szögek. Ezzel a feladatot megoldottuk.

 

Megjegyzések. 1. Azok a versenyzők, akik számolásmentes utat követtek a feladat megoldásában, az elégségesség bizonyításánál többnyire adottnak tekintettek három egy pontból induló, nem egy síkban fekvő félegyenest, amelyek közti szögek hegyesszögek és összegük ${180}^{\circ }\mathrm{.}$ Ekkor nem is használták azt a feltételt, hogy a szögek hegyesszögek. Valójában ez éppen annak a belátásához kell, hogy tetszés szerinti három hegyesszöghöz, amelyek összege ${180}^{\circ }\mathrm{,}$ van három olyan félegyenes, amelyek éppen ekkora szöget zárnak be. Emögött pedig az rejlik, hogy egy háromél élei közti szögek közül bármelyik kettő összege nagyobb a harmadiknál.
2. A megoldás gondolatmenetével tetszés szerinti tetraéderre belátható, hogy a szemközti élpárok felezőpontjait összekötő szakaszoknak ‐ a tetraéder középvonalainak ‐ közös a felezőpontja. A középvonalak a tetraéder bennfoglaló paralelepipedonjának egy csúcsból induló éleivel párhuzamosak és egyenlők. Így akkor és csak akkor merőlegesek páronként, ha a tetraéder egyenlőoldalú.

 

2. Legyen az $n$ a kettőnél nagyobb pozitív egész szám. Melyik az a legnagyobb $h$ érték, és melyik az a legkisebb $H$ érték, amelyekre igaz, hogy

$\begin{array}{c}{\displaystyle h<\frac{a_1}{a_1+a_2}+\frac{a_2}{a_2+a_3}+\text{...}+\frac{a_n}{a_n+a_1}<H}\end{array}$

(1)

bármilyen pozitív számok legyenek is $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}{a}_n?$

 

I. megoldás. Nézzük két egymás utáni tag összegét:

$\begin{array}{c}{\displaystyle \frac{a_i}{a_i+a_{i+1}}+\frac{a_{i+1}}{a_{i+1}+a_{i+2}}\mathrm{,}}\end{array}$

itt az utolsó tag utánin az elsőt értve. Ennek megfelelően $a_{n+1}\mathrm{,}{a}_{n+2}$ jelentsen $a_1$-et, ill. $a_2$-t. A két tag összege legalább $\mathrm{1,}$ ha $a_{i+2}\leqq a_i\mathrm{,}$ és legfeljebb $\mathrm{1,}$ ha $a_{i+2}\geqq a_i\mathrm{.}$
Válasszuk $i$-t úgy, hogy $a_{i+2}$ az előforduló legkisebb érték legyen. Ekkor a kiszemelt két tag összege legalább $1.$ A többi tag mind pozitív, és feltétel szerint van még legalább egy tag, így az összeg mindig nagyobb, mint $1.$ Ha viszont $i$-t úgy választjuk, hogy $a_{i+2}$ az előforduló legnagyobb érték legyen, akkor a kiválasztott két tag összege legfeljebb $1;$ miután a további $n-2$ tag mindegyike kisebb $1$-nél, igy azt kapjuk, hogy az összeg mindig kisebb, mint

$\begin{array}{c}{\displaystyle 1+n-2=n-1.}\end{array}$

Megmutatjuk, hogy az összeg mind a két korláthoz tetszés szerint közel kerülhet, ha az $a_i$ sorozatot alkalmasan választjuk. Az

$\begin{array}{c}{\displaystyle a_i=q^{i-1}\mathrm{,}i=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}n}\end{array}$

pozitív $q$ hányadosú mértani sorozathoz tartozó $S_q$ összeg :

$\begin{array}{c}{\displaystyle S_q=\frac{n-1}{1+q}+\frac{q^{n-1}}{q^{n-1}+1}\mathrm{.}}\end{array}$

Becsüljük ezt felülről. Bármilyen (kis) pozitív szám is $p\mathrm{,}$

$\begin{array}{c}{\displaystyle S_q<\frac{n-1}{1+q}+1<1+\frac{n-1}{q}<1+p\mathrm{,}\text{ha}q>\frac{n-1}{p}\mathrm{.}}\end{array}$

Másrészt alulról becsülve $S_q$-t

$\begin{array}{c}{\displaystyle S_q>\frac{n-1}{1+q}=n-1-\frac{q\left(n-1\right)}{1+q}>\left(n-1\right)-\left(n-1\right)q>n-1-p\mathrm{,}\text{ha}q<\frac{p}{n-1}\mathrm{.}}\end{array}$

Ezzel beláttuk, hogy a feladatban kérdezett értékek : $h=\mathrm{1,}H=n-1.$

 

Megjegyzések. 1. A vizsgált összeg felvesz minden értéket 1 és $n-1$ között. Ez igaz már a mértani sorozathoz tartozó $S_q$ összegre, hiszen ez pozitív $q$-kra $q$-nak folytonos függvénye, amelyik felvesz $n-1$-hez tetszés szerint közeli értékeket is és $1$-hez tetszés szerint közelieket is, tehát minden közbenső értéket is.
2. A további megoldásokban csak azt bizonyítjuk, hogy a kérdéses összeg $1$ és $n-1$ közé esik. Az, hogy ezek a korlátok nem javíthatók, ugyanúgy látható be, mint az I. megoldásban.

 

II. megoldás. Fel fogjuk használni, hogy ha $x/y<\mathrm{1,}$ és $x\mathrm{,}y$ pozitív, továbbá $z$ is pozitív szám, akkor

$\begin{array}{c}{\displaystyle \frac{x}{y}<\frac{x+y}{y+z}\mathrm{.}}\end{array}$

Valóban

$\begin{array}{c}{\displaystyle \frac{x}{y}=\frac{x}{y}\left(y+z\right)\frac{1}{y+z}=\left(x+\frac{x}{y}z\right)\frac{1}{y+z}<\frac{x+z}{y+z}\mathrm{.}}\end{array}$

Jelöljük a rövidség kedvéért az $a_1+a_2+\text{...}+a_n$ összeget $S$-sel. Egyfelől csökkentjük az $i$-edik törtet, ha a nevezőjéhez hozzáadjuk az $S-a_i-a_{i+1}$ összeget, másfelől növeljük, ha ezt az összeget a számlálóhoz is, a nevezőhöz is hozzáadjuk. Így a következő kettős egyenlőtlenséget kapjuk:

$\begin{array}{c}{\displaystyle \frac{a_i}{S}<\frac{a_i}{a_i+a_{i+1}}<\frac{S-a_{i+1}}{S}\mathrm{.}}\end{array}$

Itt $a_{n+1}$ ismét $a_1$-et jelent. Összeadva az egyenlőtlenségpárokat $i=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}n$-re a bal oldalon $1$-et, a jobb oldalon $n-1$-et kapunk, vagyis a kívánt egyenlőtlenséget.

 

III. megoldás. Jelöljük $T_n$-nel a feladatban szereplő összeget és az
$a_n\mathrm{,}{a}_{n-1}\mathrm{,}\text{...}\mathrm{,}{a}_1$ fordított sorrendben vett sorozathoz tartozót $T_n^{\text{'}}$-vel. Mind a két összeg törtjeiben ugyanazok a nevezők lépnek fel, és a két összeg azonos nevezőjű törtjeinek az összege $\mathrm{1,}$ így

$\begin{array}{c}{\displaystyle T_n+T_n^{\text{'}}=n\mathrm{.}}\end{array}$

Így ha megmutatjuk, hogy a szóban forgó összeg mindig nagyobb, mint $\mathrm{1,}$ akkor ez igaz $T_n^{\text{'}}$-re is, tehát

$\begin{array}{c}{\displaystyle T_n=n-T_n^{\text{'}}<n-1.}\end{array}$

Teljes indukcióval bizonyítjuk, hogy $1$ alsó korlát. Az $n=3$ esetben közös nevezőre hozva az összeget, és számlálót, nevezőt tagokra bontva a nevező minden tagja előfordul a számlálóban is legalább akkora együtthatóval. A számításokat elvégezve:

$\begin{array}{c}{\displaystyle T_3=1+\frac{a_1{a}_2{a}_3+a_1^2{a}_2+a_2^2{a}_3+a_3^2{a}_1}{\left(a_1+a_2\right)\left(a_2+a_3\right)\left(a_3+a_1\right)}>1.}\end{array}$

Tegyük most fel, hogy az $n$ pozitív számból képezett összegek mindig $1$-nél nagyobbak, ahol $n\geqq 3.$ Ekkor elég azt megmutatnunk, hogy az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_{n+1}$ számokból képezett $T_{n+1}$ összeg nagyobb az első $n$ számból képezettnél. De

${\displaystyle \begin{array}{c}\hfill {\displaystyle T_{n+1}-T_n=\frac{a_n}{a_n+a_{n+1}}+\frac{a_{n+1}}{a_{n+1}+a_1}-\frac{a_n}{a_n+a_1}=}\hfill \\ \hfill {\displaystyle =\frac{a_n}{a_n+a_{n+1}}+\frac{a_{n+1}}{a_{n+1}+a_1}+\frac{a_1}{a_1+a_n}-1>\mathrm{0,}}\hfill \end{array}}$

mert a három tört összege az $a_n\mathrm{,}{a}_{n+1}\mathrm{,}{a}_1$ számokból képezett összeg, és erről már beláttuk, hogy mindig nagyobb $1$-nél. Így, felhasználva az indukciós feltevést is,

$\begin{array}{c}{\displaystyle T_{n+1}>T_n>\mathrm{1,}}\end{array}$

és ezt kellett bizonyítanunk.

 

Megjegyzések. 1. Az utolsó bizonyítást lényegesen egyszerűsíthettük volna egyrészt azzal az észrevétellel, hogy $T_{n+1}$ nem változik meg, ha a számokat ciklikusan cseréljük. Így választhatjuk a sorrendet úgy, hogy $a_{n+1}$ az előforduló legkisebb érték legyen. Ekkor a $T_{n+1}-T_n$ különbségben az első tag nem kisebb a kivonandónál, a különbség tehát pozitív. Másrészt képezhető a szóban forgó összeg két számból is és az értéke $\mathrm{1,}$ így minden $2$-nél nagyobb $n$-re már $1$-nél nagyobb. Ezzel elkerülhető minden számolás.
A fenti megoldás viszont azt mutatja, hogy az indukciós bizonyítás minden további fogás nélkül is célra vezet. így viszont a $3$ tag esetére nem lett volna érdemes elkerülni a kiszámolást, mert azt a megoldás második részében is fel tudtuk használni.
2. A vizsgált összeg valójában csak az $a_{i+1}/a_i$ hányadosoktól függ. Jelöljük ezeket $b_i$-vel $i=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}n-1$-re és legyen $b_n=a_n/a_1\mathrm{.}$ Ekkor a vizsgált összeg az

$\begin{array}{c}{\displaystyle \frac{1}{1+b_1}+\frac{1}{1+b_2}+\text{...}+\frac{1}{1+b_n}}\end{array}$

alakot ölti, és itt

$\begin{array}{c}{\displaystyle b_1{b}_2\text{...}{b}_n=1.}\end{array}$

Vonjuk össze az utolsó két tagot:

$\begin{array}{c}{\displaystyle \frac{1}{1+b_{n-1}}+\frac{1}{1+b_n}>\frac{1+b_{n-1}+b_n}{1+b_{n-1}{b}_n+b_{n-1}+b_n}>\frac{1}{1+b_{n-1}{b}_1}}\end{array}$

a II. megoldásban alkalmazott megjegyzés alapján. Ezt beírva az összegbe a $b_1\mathrm{,}\text{...}\mathrm{,}{b}_{n-2}\mathrm{,}{b}_{n-1}{b}_n$ számokból képezett $n-1$-tagú összeget kapjuk, és a számok szorzata továbbra is $1.$ Ennek alapján újabb teljes indukcíós bizonyítást nyerhetünk.

 

3. $A$ és $B$ a következő játékot játssza: az első 100 pozitív egész közül véletlenszerűen kiválasztanak $k$ darabot és ha ezek összege páros, akkor $A$ nyer, egyébként pedig $B\mathrm{.}$ A $k$ milyen értékeire lesz egyenlő $A$ és $B$ nyerési esélye?

 

I. megoldás. Az első $100$ pozitív egész szám közül kiválasztható $k$-asok közül úgy választunk ki csoportokat, ameddig tudunk, hogy egy-egy csoportban ugyanannyinak az összege legyen páros, mint amennyié páratlan. Válasszuk ki először azokat, amelyekben szerepel vagy az $1$ vagy a $\mathrm{100,}$ de nem mind a kettő. Ezeket párokba állíthatjuk úgy, hogy az első $98$ szám közül kiválasztott egy-egy $k-1$-eshez egyszer az $1$-et, egyszer a $100$-at vesszük $k$ -adiknak. Ekkor minden pár egyik $k$-asának az összege páros, a másiké páratlan.
A maradó $k$-asok közül vegyük azokat, amelyek a $2$ és a $99$ közül az egyiket tartalmazzák, a másikat nem. Ezek közül is ugyanannyinak az összege páros, mint amennyié páratlan, az előbbi gondolatmenet szerint. Az eljárást tovább ismételjük a $\mathrm{3,}\mathrm{98,}$ a $\mathrm{4,}\mathrm{97,}\text{...}\mathrm{,}$ az $\mathrm{50,}51$ párral. Ezután már csak olyan $k$-asok maradnak meg, amelyek a kiválasztáshoz használt párok közül bizonyosaknak mindkét eleméből tevődnek össze. Ilyenek csak páros $k$ esetén vannak, tehát páratlan $k$ esetén $A$-nak és $B$-nek egyenlő esélye van a nyerésre.
Páros $k$ esetén azok a $k$-asok maradnak meg, amelyek az említett $50$ pár közül $k/2$-nek mindkét eleméből állnak. Mivel mindegyik pár két elemének összege $\mathrm{101,}$ tehát páratlan szám, így mindegyik fennmaradt k-as elemeinek összege páros, ha $k/2$ páros és páratlan, $k/2$ páratlan. Ezek szerint $A$-nak nagyobb a nyerési esélye, ha $k$ osztható $4$-gyel, ha viszont $k4$-gyel osztva $2$ maradékot ad, akkor $B$ esélye nagyobb a nyerésre.

 

Megjegyzések. 1. Az elmondottak alapján ki is számíthatjuk, ki hány esetben nyer. A kiválasztható $k$-asok száma $\left(\genfrac{}{}{0ex}{}{100}{k}\right)$ és, ha $k$ páros, akkor $\left(\genfrac{}{}{0ex}{}{50}{k/2}\right)$-vel több esetben nyer az egyik játékos, mint a másik. Így páratlan $k$ esetén mindegyikük

$\begin{array}{c}{\displaystyle \frac{1}{2}\left(\genfrac{}{}{0ex}{}{100}{k}\right)}\end{array}$

esetben nyer, páros $k$ esetén pedig az egyikük és másikuk számára kedvező esetek száma

$\begin{array}{c}{\displaystyle \frac{1}{2}\left(\left(\genfrac{}{}{0ex}{}{100}{k}\right)-\left(\genfrac{}{}{0ex}{}{50}{k/2}\right)\right)\mathrm{,}\text{ill.}\frac{1}{2}\left(\left(\genfrac{}{}{0ex}{}{100}{k}\right)+\left(\genfrac{}{}{0ex}{}{50}{k/2}\right)\right)\mathrm{.}}\end{array}$

2. Az eljárás alkalmazható akkor is, ha $100$ helyett bármilyen páros $N$ számot mondunk. A válasz ekkor is ugyanaz, mint a $100$ esetében volt. Ha páratlan $N$ számot veszünk $100$ helyett, akkor már sohasem egyenlők a nyerési esélyek. Ilyenkor $1$ és $N-\mathrm{1,}$ majd $2$ és $N-\mathrm{2,}3$ és $N-3$ és így tovább, ismét használhatók egyenlő esélyt adó $k$-asok kiválasztására. A fennmaradó $k$-asok közül külön kell foglalkozni azokkal, amelyekben előfordul az $N\mathrm{.}$ A részletek végiggondolását az olvasóra bízzuk. $B$-nek nagyobb a nyerési esélye, ha $k4$-gyel osztva $1$ vagy $2$ maradékot ad, különben $A$-nak.

 

II. megoldás. Vizsgáljuk az $\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}2N$ számok közül kiválasztható $k$-asokat. Jelöljük $D\left(N\mathrm{,}k\right)$-val a páros, illetve a páratlan összegű $k$-asok számának a különbségét. Erre a függvényre állapítunk meg egy rekurzív összefüggést. Legyen $k\leqq 2N-2.$ Csoportosítsuk a $k$-asokat aszerint, hogy hány számot tartalmaznak a $\left(2N-\mathrm{1,}2N\right)$ párból. Az első csoportba tartozzanak azok a $k$-asok, amelyek tartalmazzák mind a kettőt, a másodikba azok, amelyek egyiket sem tartalmazzák, a harmadikba pedig azok, amelyek az egyiket tartalmazzák, a másikat nem.
A harmadik csoportbeli $k$-asoknak $k-1$ eleme nem nagyobb $2N-2$-nél, és minden ilyen $k-1$-es a $2N-1$-gyel és a $2N$-nel is $k$-assá egészíthető ki. Az elemek összege a két $k$-as közül az egyikben páros, a másikban páratlan. A harmadik csoportban tehát ugyanannyi páros összegű $k$-as van, mint páratlan összegű, így ezek járuléka $D\left(N\mathrm{,}k\right)$ értékéhez $0.$
A második csoport $k$-asai csupa $2N-2$-n él nem nagyobb számból állnak, ezek tehát $D\left(N-\mathrm{1,}k\right)$-t adnak $D\left(N\mathrm{,}k\right)$ értékéhez.
Az első csoport minden $k$-asa $k-2$ elemet tartalmaz, amelyek nem nagyobbak $2N-2$-nél, továbbá a $2N-1$-et és a $2N$-et. Az első $k-2$ elem összegét tekintve a vizsgált különbség $D\left(N-\mathrm{1,}k-2\right)\mathrm{.}$ A $k$-asokban még $2N-1+2N\mathrm{,}$ tehát páratlan szám adódik az összeghez, így annak párossága az ellenkezőjére változik. Az első csoport $k$-asai, tehát $-D\left(N-\mathrm{1,}k-2\right)$-vel járulnak hozzá $D\left(N\mathrm{,}k\right)$ értékéhez. Ezzel a következő összefüggést kaptuk:

$\begin{array}{c}{\displaystyle D\left(N\mathrm{,}k\right)=D\left(N-\mathrm{1,}k\right)-D\left(N-\mathrm{1,}k-2\right)\mathrm{.}}\end{array}$

(3)

Az összefüggés $k=2N-1$-re és $k=2N$-re is helyes, ha megállapodunk abban, hogy ha $k>2N\mathrm{,}$ akkor $D\left(N\mathrm{,}k\right)$ jelentsen $0$-t.
Ennek alapján teljes indukcióval igazoljuk a következő állítást: $D\left(N\mathrm{,}k\right)$ pozitív, ha $k$ osztható $4$-gyel, negatív, ha $k$ páratlan szám kétszerese, és $\mathrm{0,}$ ha $k$ páratlan. Belátjuk először, hogy ez $k=\mathrm{1,}\mathrm{2,}3$ és $4$-re igaz. ($2N$ tetszőleges, $k$-nál nem kisebb páros szám.)
$k=1$-re $N$ páros szám van az adottak közt és $N$ páratlan, így $D\left(N\mathrm{,}1\right)=0.$ Párokat választva ki, akkor lesz az összeg páros, ha vagy mind a két szám páros, vagy mind a kettő páratlan, és akkor lesz páratlan, ha az egyik szám páros, a másik páratlan. Az előbbi és az utóbbi típusú párok száma $2\left(\genfrac{}{}{0ex}{}{N}{2}\right)=N\left(N-1\right)\mathrm{,}$ ill. $N^2\mathrm{,}$ tehát $D\left(N\mathrm{,}2\right)=-N<0.$ Ezek az értékek $N=1$-re is helyesek.
Három szám összege páros, ha mindegyik szám páros, vagy egyikük páros, a másik kettő páratlan; viszont páratlan az összeg, ha mindegyik szám páratlan, vagy ha egyikük páratlan, a másik kettő pedig páros. Mivel a páros és páratlan számok száma egyenlő, így a kétféle hármasok száma is megegyezik, tehát

$\begin{array}{c}{\displaystyle D\left(N\mathrm{,}3\right)=0.}\end{array}$

Ha $k=\mathrm{4,}$ akkor páros összeget kapunk, ha mind a $4$ páros, vagy mind a $4$ páratlan, vagy közülük $2$ páros, $2$ páratlan. Páratlan lesz az összeg, ha a $4$ szám között $1$ páratlan van, vagy ha $1$ páros van. Az egyik-, ill. másikféle esetek száma

${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\left(\genfrac{}{}{0ex}{}{N}{4}\right)+{\left(\genfrac{}{}{0ex}{}{N}{2}\right)}^2}& {\displaystyle =\frac{N\left(N-1\right)\left(N-2\right)\left(N-3\right)}{12}+\frac{N^2{\left(N-1\right)}^2}{4}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{N\left(N-1\right)\left(2N^2-4N-3\right)}{6}\mathrm{,}}\hfill \end{array}}$

illetőleg

$\begin{array}{c}{\displaystyle 2N\left(\genfrac{}{}{0ex}{}{N}{3}\right)\frac{N^2\left(N-1\right)\left(N-2\right)}{3}=\frac{N\left(N-1\right)\left(2N^2-4N\right)}{6};}\end{array}$

$N=2$ esetén az esetek száma $\mathrm{1,}$ ill. $0.$ Eszerint

$\begin{array}{c}{\displaystyle D\left(N\mathrm{,}4\right)=\frac{n\left(N-1\right)}{2}>0.}\end{array}$

A vizsgált $k$ értékek esetén tehát minden szóba jövő $N$-re igaz az állítás. Ekkor egyszersmind $N=1$ és $N=2$-re minden szóba jövő $k$ esetén igaz az állítás.
Tegyük most fel, hogy $M>\mathrm{2,}K>4$ és igaz az állítás, ha $k<K\mathrm{,}$ továbbá az $M$-nél kisebb $N$-ekre tetszés szerinti szóba jövő $k$ mellett. A (3) összefüggés szerint

$\begin{array}{c}{\displaystyle D\left(M\mathrm{,}K\right)=D\left(M-\mathrm{1,}k\right)-D\left(M-\mathrm{1,}K-2\right)\mathrm{.}}\end{array}$

Ha $K$ páratlan, akkor $K-2$ is, így feltevés szerint a jobb oldal mindkét tagja $\mathrm{0,}$ tehát $D\left(M\mathrm{,}K\right)$ is az. Ha $K$ páros, akkor $K-2$ is, és feltevés szerint $D\left(M-\mathrm{1,}K\right)\mathrm{,}$ ha nem $0$ (ti. ha $M=K$), ellenkező előjelű, mint $D\left(M-\mathrm{1,}K-2\right)\mathrm{.}$ Az indukciós feltételből az is következik, hogy $D\left(M-\mathrm{1,}K-2\right)$ nem $0.$ Azt kaptuk tehát, hogy $D\left(M\mathrm{,}K\right)$ sem $\mathrm{0,}$ és ellenkező előjelű, mint $D\left(M-\mathrm{1,}K-2\right)\mathrm{.}$ Ez azonban azt jelenti, hogy az állítás helyessége öröklődik $M$ és $K$-ra. A kimondott állítás tehát minden szóba jövő $N\mathrm{,}k$ értékpárra igaz.

 

Megjegyzések. 1. Felesleges volt $D\left(N\mathrm{,}3\right)$ és $D\left(N\mathrm{,}4\right)$ kiszámítása, mert az indukciós bizonyítás már ezekre is adja az állítás helyességét. Jónak láttuk azonban mind a $4$ lehetséges esetre bemutatni egy-egy példát. Aki nem tartja erőszakoltnak a $k=0$ eset megengedését, ezt tekintheti a $k=2$ helyett további egyszerűsítésként.
2. A teljes indukciónak itt egy ritkábban előforduló esetével találkoztunk, a két változó szerint egyidejűleg futó teljes indukcióval, hiszen mikor $M$-re és $K$-ra bizonyítottuk az öröklődést, fel kellett használnunk azt is, hogy $M-1$-re és ugyanerre a $K$-ra igaz az állítás. Így tulajdonképpen a $k=2$ eset után $k=3$-ra és minden $N$-re, majd $K=4$-re és így tovább adódik az állítás helyessége. Ehhez viszont kell az, hogy a legkisebb $N$ értékre minden szóba jövő $k$ esetén igaz legyen az állítás. Esetünkben ez mindössze az $N=\mathrm{1,}k=\mathrm{1,}2$ eseteket jelentette. Annyiban is speciális volt ez a bizonyítás, hogy $M$-re a $K$-nál kisebb $k$-kra nem volt szükséges felhasználnunk az indukciós feltevést.

 

III. megoldás. Az előző megoldásban bevezetett jelöléssel $D\left(\mathrm{50,}k\right)$-t kapcsolatba hozhatjuk az

$\begin{array}{c}{\displaystyle 1+{\left(-1\right)}^{c}x\mathrm{,}c=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}100}\end{array}$

elsőfokú polinomok szorzatával. Ebben úgy kapjuk a $k$-adfokú tagokat, hogy $k$ tényezőből az $x$-es tagot vesszük, a többiből az $1$-et, ezeket összeszorozzuk és az összes ilyen tagot összeadjuk. Egy-egy ilyen tagban $x^k$ együtthatója $-1$-nek a $c_1+c_2+\text{...}+c_k$-adik hatványa, ahol az összeadandók különböző, $100$-nál nem nagyobb egészek. Az együttható tehát $\mathrm{1,}$ ha az összeg páros, $-\mathrm{1,}$ ha az összeg páratlan. Eszerint $x^k$ együtthatója a szorzatban éppen $D\left(\mathrm{100,}k\right)\mathrm{.}$
A szorzat másfelől felváltva $1+x$ és $1-x$ tényezők szorzata, vagyis

$\begin{array}{c}{\displaystyle {\left(1-x^2\right)}^{50}=1-50x^2+\text{...}+{\left(-1\right)}^j\left(\genfrac{}{}{0ex}{}{50}{j}\right)x^{2j}+\text{...}+x^{100}\mathrm{.}}\end{array}$

Eszerint egyenlők a nyerési esélyek, ha $k$ páratlan, $\left(\genfrac{}{}{0ex}{}{50}{j}\right)$-vel több esetben nyer $A\mathrm{,}$ mint $B\mathrm{,}$ ill. $B\mathrm{,}$ mint $A\mathrm{,}$ ha $k=2j$ és $j$ páros, ill. páratlan.

 

Megjegyzés. Az $F\left(k\right)=D\left(\mathrm{100,}k\right)$ függvényt úgy sikerült meghatároznunk, hogy hozzárendeltük az

$\begin{array}{c}{\displaystyle F\left(x\right)=1+f\left(1\right)x+f\left(2\right)x^2+\text{...}+f\left(100\right)x^{100}}\end{array}$

polinomot, amit sikerült más alakba írni és abból $f$ értékeit meghatározni. $F$-et az $f$ generátor függvényének nevezzük. A generátorfüggvény gondolata és számos érdekes alkalmazása Leonhard Euler (1707 ‐ 1783) rendkívül termékenynek bizonyult felfedezése, ami a matematika számos ágában alapvető szerepet kapott. Feladatunkban alkalmazható $100$ helyett tetszés szerinti $N$ számra, és az I. megoldáshoz fűzött 2. megjegyzésben kimondott eredményre vezet. A számolás elvégzését az olvasóra bízzuk.
Surányi János

Helyesbítés

Az 1985/86-os évi pontverseny iskolák szerinti összesítéséből (1986/10. szám, 455 ‐ 456. oldal) sajnálatos módon kimaradt a Landler Jenő Gimnázium (Budapest, XIX.) tanulóinak eredménye. Az iskolából 3 tanuló (dr. Marosvári Péter tanár tanítványai) összesen 260 pontot szerzett.
Ezúton kérjük az érintettek szíves elnézését.
A szerkesztőség

---

^{${}^{*}$}Lásd: Hajós Gy. ‐Neukomm Gy. ‐ Surányi J. : Matematikai versenytételek, II. köt., 2. kiad. (Tankönyvkiadó, Budapest, 1965.) 65 - 66. old.