Kezdőlap


Cím:	Háromjegyű kódok és irányított gráfok (fordította Kende Gábor)
Szerző(k):	Gerver, M. L.
Füzet:	1987/december, 433 - 439. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi cikk a Kvant M 1002-es feladatának megoldásával foglalkozik. A feladat szövege :
a) Egy szórakozott matematikus elfelejtette lakása biztonsági zárának három jegyű kódját. (A záron a $0, ..., 9$ számjegyek találhatók, s ha ezek közül sikerül a három megfelelőt a helyes sorrendben megnyomnia, az ajtó kinyílik, függetlenül a megelőző, sikertelen próbálkozásoktól.) Így most sorra nyomkodja a gombokat ─ másodpercenként egyet-egyet. Meg van győződve arról, hogy még abban a legkedvezőtlenebb esetben sem kényszerül $16$ perc $42$ másodpercnél (ami $1002$ másodperc) hosszabb várakozásra, ha a helyes kombinációt próbálná utoljára. Igaza van-e? Milyen módszerrel nyithatja ki leggyorsabban az ajtót?
Hogyan módosítható az állítás, ha
b) csak az $1, 2, 3$ -as gombok fordulhatnak elő a kódban?
c) a matematikus emlékszik, hogy a kód három különböző számjegyből állt?

(Ennek a feladatnak a nyomán készült a Gy. 2398. gyakorlat, amelynek megoldása a KÖMAL 1987. novemberi számának 391. oldalán olvasható. Szerk.)

Megjegyzések a feladat feltételeihez

Mindhárom részfeladatban két kérdésre kell válaszolnunk:
1. mennyi idő szükséges ‐ a legkedvezőtlenebb esetben ‐ a zár kinyitásához?
2. milyen módszerrel csökkenthető a próbálkozások ideje a legrövidebbre?
Ebben a cikkben megadjuk a választ az első kérdésre; a második, mint majd látni fogjuk, még pontosításra szorul: mindenesetre mutatunk egy módszert a szórakozott matematikus kisegítésére, és az is kiderül, milyen értelemben kellene javítani rajta.

A megoldás ötlete

A szóba jöhető háromjegyű kódok száma nyilván ezer. Mindegyiküket kipróbálva előbb vagy utóbb rábukkanunk az elfelejtett kódra, de ez akár 3000 másodpercig is eltarthat, ami majdnem háromszorosa a tervezett 1002 másodpercnek!
Hogyan lehet hát elég az 1002 másodperc? És elég-e egyáltalán?
Vegyük észre, hogy ha például sorra megnyomjuk az 1-es, 2-es, ..., majd a
9-es gombot, akkor nem három kombinációt próbáltunk ki (123, 456, 789), hanem
hetet (123, 234, 345, 456, 567, 678, 789). A kapott kódok egy láncot alkotnak:
mindegyikük utolsó két jegye megegyezik a következő hármas első két jegyével.
Ahhoz, hogy 1002 másodperc alatt kinyithassuk a zárat, ilyen láncra kellene
fűznünk az ezer háromjegyű kódot: az első másodpercben kezdhetnénk az első
kombináció kipróbálását, a másodikban a másodikét, ... az 1000.-ben az ezredikét.
Innen egyébként látható, hogy 1002 másodpercnél kevesebb nem lenne elegendő: abban az esetben, ha minden kombinációt végig akarunk próbálni, az utolsóhoz nem kezdhetünk hozzá az ezredik másodpercnél korábban.
A cél világos : sorba kellene rendeznünk az összes háromjegyű kódot úgy, hogy mindegyikük az előző hármas második két jegyével kezdődjék. De vajon elérhető-e?
Az alábbi esetben például ‐ bár a helyzet a feladatbelihez hasonló ‐ a fenti cél nem érhető el:
Tegyük fel, hogy a kód jegyei különbözőek, és csak az 1, 2, 3 számok közül kerülhetnek ki. Most tehát az 123, 132, 213, 231, 312, 321 hármasokat kell végigpróbálnunk. (Lényegében ez volt a KÖMAL Gy. 2398. gyakorlata. Szerk.) Ha találunk hozzájuk láncot, akkor 8 másodperc alatt mindenképpen végzünk. Csakhogy most ilyen lánc nincsen! Ezek a számhármasok két láncot határoznak meg (melyek ezek?), így a próbálkozásokhoz 9 másodperc kell.
A kérdés vizsgálatában és a próbálkozások megszervezésében szükségünk lesz az irányított gráfok fogalmára. Irányított gráfnak nevezünk véges sok pontot ‐ a gráf csúcsait ‐, amelyek közül néhányat irányított szakaszok ‐ a gráf élei ‐ kötnek össze. Megengedünk olyan éleket is, amelyek egy pontot önmagával kötnek össze.

T_{10}

irányított gráf

Az alábbiakban elkészítünk egy irányított gráfot, melynek segítségével eljutunk az a) feladat megoldásához. Tekintsünk 100 pontot és rendeljünk ezekhez kétjegyű sorszámokat : 00, 01, 02, ..., 98, 99. Akkor vezessen él az

a b

pontból a

d c

ponthoz, ha

b = d

, pl. (13; 38), (45; 55). Az olyan pontokból tehát, melyek sorszáma két egyforma számjegy, önmagukhoz is vezet él.
Jelölje az így kapott irányított gráfot

T_{10} .

Írjuk ezután az

a b

-ből

b c

-be mutató élre az

a b c

háromjegyű kódot:

{a b}^{\binom{a b c}{\to}} b c

(

13^{\binom{138}{\to}} 38 .)

Ekkor minden háromjegyű kód pontosan egyszer fordul elő: a 455 például a 45-ből az 55-be mutató élre van felírva. Maga

T_{10}

100 csúcsból és 1000 élből áll; utóbbiakra felírtuk az összes háromjegyű kódot. Látható, hogy minden csúcsból 10 él indul, és minden csúcsba 10 él fut be: ab-ből az ab0, ab1, ..., ab9 élek lépnek ki, az ide futó élek pedig : 0ab, 1ab, ..., 9ab.
Az is látszik, hogy irányított élek mentén haladva egy tetszőleges ab csúcsból bármely cd csúcsba eljuthatunk:

\begin{matrix} {a b}^{\binom{a b c}{\to}} {bc}^{\binom{b c d}{\to}} cd . \end{matrix}

Az ilyen irányított gráfokat erősen összefüggőnek nevezzük.
Vegyük észre, hogy ha sikerül úgy bejárnunk

T_{10}

-et, hogy minden élén pontosan egyszer menjünk végig, akkor egyben elértük kitűzött célunkat is: egyetlen láncba fűztük az összes háromjegyű kódot.
Ilyen útvonal létezését állítja az

Euler-vonal tétele

Nevezzünk egy irányított gráfot szabályosnak, ha bármely A csúcsából ugyanannyi él indul ki, mint amennyi befut ide: jelöljük ezt az értéket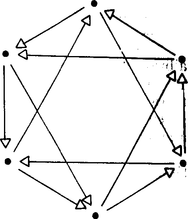

p_{A}

-val.

1. ábra

T_{10}

-ben például minden ab csúcsra

p_{a b} = 10

; az 1. ábrán látható erősen összefüggő szabályos irányított gráfban minden

A

csúcsra

p_{A} = 2

.
Tétel: erősen összefüggő, szabályos irányított gráfban mindig található olyan kör ‐ azaz zárt út az irányított élek mentén ‐, amely a gráf minden élén pontosan egyszer halad át.
Az ilyen köröket nevezzük Euler-vonalnak,vagy Euler-körnek.

A tétel bizonyítása

Szemeljük ki a gráf egy tetszőleges

A

csúcsát, és induljunk el innen az irányított élek mentén, "felégetve magunk mögött a hidakat'', azaz kiradírozva mindazokat az éleket, amelyeken már áthaladtunk. Lévén az élek száma véges, előbb-utóbb elakadunk: olyan csúcsba érünk, ahonnan már nem vezet ki él. Mivel minden csúcsból annyi él lép ki, amennyi oda befutott, ez a "zsákutca-csúcs'' nem lehet más, mint

A

(2. ábr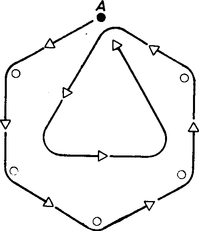a).

2. ábra

Megtett utunk így egy kör ‐ c ‐, amely A-ból indul és A-ban végződik. Mivel kiradíroztuk magunk mögött a bejárt útszakaszokat, biztos, hogy a kör a gráfnak egy élét sem tartalmazza kétszer. A megmaradó irányított gráf pedig nyilván továbbra is szabályos marad.
Ha c a gráf összes élét tartalmazza, akkor Euler-kör, így teljesül a tétel állítása.
Ha nem, akkor a c kör által érintett csúcsok között van olyan

A_{1}

csúcs, amelynek maradt ki nem radírozott kijárata ‐ jelölje ezt

S_{1}

. (Ha nincs ilyen csúcs, akkor a vizsgált irányított gráf nem lehet erősen összefüggő.)
Induljunk el most

A_{1}

-ből, megint kiradírozva a bejárt éleket; most is zsákutcába érünk, ami a fentiek szerint csak

A_{1}

lehet; így kapunk egy

c_{1}

kört, melynek kezdő- és végpontja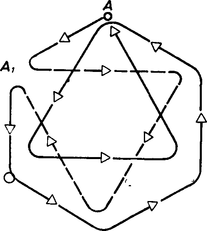

A_{1}

3. ábra

c-t és

c_{1}

-et egyetlen C körré egyesíthetjük (3. ábra), ha a c körön

A_{1}

-hez érve először

c_{1}

-en megyünk végig, s csak ezután a c kör

A_{1} A

szakaszán.
Ha C tartalmazza az eredeti gráf minden élét, teljesül a tétel állítása. (A 3. ábrán ez a helyzet.) Ellenkező esetben a C által érintett csúcsok között kell legyen olyan

A_{2}

, melynek maradt kijárata ‐

S_{2}

‐ s. í. t.
Hasonlóan növelve a kört, előbb-utóbb elfogynak a gráf élei, a tétel tehát igaz, a bizonyítást befejeztük.
A hozzáértők bizonyára észrevették, hogy a teljes indukció módszerét felhasználva bizonyításunk precízebb és rövidebb lehetett volna. Egy elegáns ‐ bár lényegében a bemutatottal megegyező ‐ gondolatmenet kiindulása a következő: vegyük a leghosszabbat azon körök közül, amelyek egyetlen élen sem mennek át kétszer ...
Az általunk választott bizonyítás azonban módszert is ad Euler-kör megtalálására.

Keressük

t_{min} - t

Vegyük most sorra az a), b) és a c) feladatokat.
a) Mivel

T_{10}

szabályos, erősen összefüggő irányított gráf, létezik benne e Eulerkör, amely a gráf 1000 élének mindegyikén pontosan egyszer halad át. Válasszunk egy tetszőleges háromjegyű számot, és járjuk be a gráf éleit a kiválasztott számú élen indulva e mentén. Az érintett élek sorszámai a háromjegyű kódok keresett sorozatát adják, amely tehát tartalmazza az összes háromjegyű számot, s minden eleme ‐ az elsőt kivéve ‐ az őt a sorban megelőző kód második két jegyével kezdődik.
b)

T_{10}

-hez hasonlóan kapható a

T_{3}

irányított gráf: ennek 9 csúcsa az 1, 2, 3 számjegyekből készíthető kétjegyű számok, 27 élét pedig az 1, 2, 3 jegyekből álló összes háromjegyű számokkal jelölhetjük meg.

T_{3}

-ban is létezik Euler-kör (ilyen látható a 4. ábrán), így a b) feladatban

t_{min} = 29

sec.

4. ábra

Általában, n gomb és háromjegyű kód esetén a megfelelő

T_{n}

irányított gráfnak

n^{2}

csúcsa és

n^{3}

éle lesz, s így

t_{min} = (n^{3} + 2)

sec.
c) Ha azt is tudjuk, hogy az elfelejtett háromjegyű kód számjegyei különbözők, akkor n gomb

(n ≧ 3)

esetén

n (n - 1) (n - 2)

ilyen számhármas van ; az

n = 3

esetben ‐ melyet a megoldás ötletének bemutatásakor ismertettünk ‐ ez 6 különböző kódot jelent, míg a feladat szerinti n=10 esetben 720-at.
Vegyünk fel

n (n - 1)

pontot; jelöljük őket olyan kétjegyű számokkal, melyek jegyei különbözőek; n=3-ra így 6 pontot kapunk: 12, 13, 21, 23, 31, 32; n=10-re 90 pontot: 01, 02, ..., 09; 10, 12,..., 19; ...; 90, 91, ..., 98. Vezessen él ab-ből dc felé, ha b = d és

a \neq c

; írjuk az él fölé most is az abc kódot.Vegyük észre, hogy a konstrukció miatt a, b és c páronként különbözőek.
Az így kapott szabályos irányított gráf (jelölje

D_{n}

) minden

a b

csúcsára nyilván

p_{a b} = n - 2

(5. ábra).

5. ábra

6. ábra

n > 3

esetén a

D_{n}

irányított gráf erősen összefüggő (bizonyítsuk!), az

n = 3

esetben azonban nem (6. ábra).

Az Euler-vonal tételéből adódik, hogy:

a c) feladatban

t_{min} = 722

másodperc (általában

n > 3

esetén

t_{min} = n (n - 1) (n - 2) + 2

másodperc);

n = 3

esetén

D_{3}

nem-összefüggő volta miatt a kódok végignézéséhez szükséges idő 1 másodperccel nő: nem 8, hanem 9 másodperc.
Megtaláltuk tehát

t_{min}

értékét mind az a), mind pedig a b) és c) feladatokban. Próbáljuk meg ugyanezzel a módszerrel megkeresni

t_{min}

értékét, ha
1. a zár 10-gombos, és tudjuk, hogy a kód három jegye közül legalább az egyik 9-es;
2. a zár 10-gombos, és tudjuk, hogy a háromjegyű kód jegyei közül pontosan kettő egyforma;
3.

2 ≦ k ≦ n

, a zár n gombos, a kód pedig k jegyű;
4. a zár 6-gombos, rajtuk a 0, 1, ..., 5 jegyekkel; a kód mindhárom jegye különböző, egyikük éppen 5.

Hogy néz ki mindez a gyakorlatban?

A fentiekből következik, hogy eljárhatunk a következőképpen :
1. Fölvesszük a megfelelő irányított gráfot (pl. az a), b), ill. c) feladatokhoz ezek rendre

T_{10}

T_{3}

és

D_{10}

).
2. Keresünk benne Euler-vonalat (jelölje ezt e).
3. Rögzítjük a gráf egy tetszőleges

S_{1}

élét és innen indulva sorra vesszük az

S_{2}, S_{3}, ... S_{n}

éleket az

e

kör mentén haladva, ahol

\begin{matrix} N = {\begin{matrix} 1000 az & a) feladatban \\ 27 a & b) feladatban \\ 720 a & c) feladatban \end{matrix} \end{matrix}

4. Följegyezzük az

S_{1}, S_{2}, ..., S_{N}

élek háromjegyű sorszámait.
Mivel

S_{i}

csak "megtoldja'' egy jeggyel

S_{i - 1}

-et, elég, ha csak ezt az egy gombot nyomjuk meg. A 4. pont tehát átfogalmazható a következőképpen:

4^{'}

. Írjuk

S_{1}

háromjegyű száma után

S_{2},

majd ezután

S_{3}

s. í. t. harmadik számjegyét ‐ egészen

S_{N}

-ig. Ily módon egy sorozathoz jutunk, mely

N + 2

jegyből áll. Ha megvan a sorozat, akkor a jegyei szerint nyomkodva a zár gombjait ‐ minden másodpercben egyet-egyet ‐

(N + 2)

másodperc, azaz

t_{min}

idő alatt végezhetünk a kérdéses kódok átvizsgálásával; azaz az elfelejtett, a zárat kinyitó számkombináció megtalálása nem tart tovább

(N + 2)

másodpercnél. Az igazi feladat tehát a megfelelő sorozat gyors elkészítése. Ha ez nagyon sokáig tart, akkor elképzelhető, hogy hősünk még mindig gyorsabban célhoz ér az összes kombináció végigpróbálásával.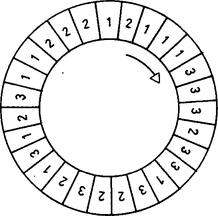

7. ábra

Ha például a

T_{3}

irányított gráf e körén a 113-as éltől ‐ tehát a 11-es csúcsból ‐ indulva megyünk végig, akkor az alábbi 29 jegyű sorozatot nyerjük (4.ábra).
113 332 331 322 321 312 311 2 221 211 1
Mivel e kör, a sorozat első és utolsó számjegypárja megegyezik. (Az ilyen számú csúcsból indul ki

S_{1}

és ide fut be

S_{N}

.) Ezért ahelyett, hogy sorba írnánk a sorozat

N + 2

jegyét, egy kör kerületére írhatjuk fel az

N

darab jegyet (p1. a 7. ábrán, ahol

N = 27

).
A 7. ábrán látható kerék peremén felírva (jelölje ezt a kereket

B

) kilenc egyest, kilenc kettest és kilenc hármast láthatunk sajátos rendben. Ez az elrendezés teljes egészében tartalmazza a b) feladat megoldását. Ehhez hasonló "bűvös'' kereket kellene szerkesztenünk, mégpedig gyorsan, az a) és a c) feladatok igazán gyors megoldásához is.

Párbeszéd a bűvös kerekekről

‐ Lássuk hát, mit is tud ez a bűvös kerék?
‐ Bármelyik számjegytől indulsz is el, ha negatív irányban haladva minden másodpercben 1 számjegyet olvasol le, akkor 29 másodperc alatt az összes olyan háromjegyű számot megkapod, amelyeket az 1, 2, 3 számjegyekkel lehet felírni.
‐ Igen, ez kell a megoldáshoz, és ezt tudnia kell a másik két feladathoz készítendő A és C keréknek is, de nem itt van a titok.
‐ Ellenkező irányban indulva is működik a kerék!
‐ Valóban, de ez az előzőekből már következik. S ugyanígy teljesülnek

T_{n}

minden Euler-körére.
‐ Ez azt jelenti, hogy a 4. ábra Euler-köre volna a rejtély kulcsa?
‐ Igen! Ez ugyanis nem az általános recept szerint készült, amely minden szabályos, erősen összefüggő irányított gráfra működik, hanem egy speciális, a

T_{n}

szimmetriáját kihasználó algoritmus felhasználásával.
‐ És vajon mit tud ez az algoritmus?
‐

n = 3

-ra még nem olyan nagy a különbség. De

T_{10}

-nek már 1000 éle van, Euler-kör keresése pedig az általános módszerrel igen hosszú és munkaigényes feladat ‐ még elektronikus számítógéppel is.
‐ És ez a speciális algoritmus gyorsabban találja meg e-t?
‐ Erről van szó ! Az A kerékre például lényegében ezer másodperc alatt tudom felírni az ezer számjegyet! Még elektronikus számítógép sem kell hozzá, elég, ha emlékszem, melyik 3‐4 számjegyet írtam fel utoljára. Majdnem olyan egyszerű a dolog, mintha csak a természetes számokat írnám fel egymás után.
‐ Ilyen gyorsan? Hát a C kerék 720 jegyű sorozata? Azt is ilyen egyszerűen és gyorsan fel tudod írni?
‐ Igen! Bár ezeket az egyszerű sorozatokat egyáltalán nem volt egyszerű kigondolni ...
... Itt félbeszakítjuk a párbeszédet, nehogy olvasóinkat megfosszuk attól az örömtől, hogy maguk találhassák ki, milyen sorrendben kerüljenek az egyes számjegyek az A és a C kerék peremére ‐ vagy az általános esetben, k-jegyű kódok és

n

nyomógomb esetén. A szöveg és az ábrák sok mindent elárulnak e sorozatok felépítésének és gyors felírásának titkairól; meglehet, olvasóinknak nem lesz ezekre szükségük és inkább a saját útjukat járják. Sok sikert!

M. L. Gerver, Kvant 87/2, 32‐35. oldal

Fordította : Kende Gábor