Kezdőlap


Cím:	Az Euler-féle összegképlet és néhány alkalmazása
Szerző(k):	Petruska György
Füzet:	1987/november, 337 - 346. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A klasszikus analízis egyik igen hasznos képletét és ennek néhány jellegzetes alkalmazását kívánja megismertetni ez a cikk az olvasóval. Közismertek (többnyire a teljes indukció alkalmazásaként) az

\begin{matrix} 1 + 2 + ... + n = \frac{n (n + 1)}{2} \\ 1^{2} + 2^{2} ... + n^{2} = \frac{n (n + 1) (2 n + 1)}{6} \\ 1^{3} + 2^{3} + ... + n^{3} = {(1 + 2 + ... + n)}^{2} = \frac{n^{2} {(n + 1)}^{2}}{4} \end{matrix}

összefüggések. Vajon a negyed-, ötöd-, és általában a magasabb fokú hatványösszegekre nem írhatók fel megfelelő eredmények? Mi történik, ha a kitevő

- 1

, azaz mekkora szám mondjuk

1 + \frac{1}{2} + ... + \frac{1}{100}

? Általánosabban,

1 + \frac{1}{2} + ... + \frac{1}{n}

értéke hogyan becsülhető? Hány jegyű szám a 10-es számrendszerben a

100! = 1 \cdot 2 \cdot ... \cdot 100

? Milyen gyorsan növekszik az

n

! sorozat? Az utóbbi kérdések és a rájuk adható válasz az egyetemi matematikatanítás témája, ám ott sem mindig derül ki, hogy a bizonyítások háttere mindig ugyanaz a módszer, Euler nevezetes összegképlete. Az összegképlet és számos alkalmazásának megértéséhez az analízis elemeire van csupán szükség, ezért kezdők számára is meggyőző a módszer hatékonysága.

2. Az Euler‐képlet legegyszerűbb esete

A képlethez vezető alapgondolat a következő: tegyük fel, hogy valamely

f

függvénynek a

0 ≦ i ≦ n

egész számokon felvett értékeinek az összegét akarjuk kiszámítani, azaz az

S = f (0) + f (1) + ... + f (n)

mennyiségre vagyunk kíváncsiak. Az

f

függvényről kikötjük, hogy elég "jó tulajdonságú'', például a [0;

+ \infty

) intervallumban differenciálható és a deriváltja is folytonos. Az

S

összeg helyett az

I = {\int_{0}^{n}}_{}^{} f (x) d x

integrált tekintjük. Ennek persze fogalmilag sokkal bonyolultabb a definíciója, mégis a gyakorlat számára jobban hozzáférhető. Érdemi eredményre persze csak úgy juthatunk, ha lehetőségünk van az

S - I

"hiba'' becslésére.
Az

{\int_{j}^{j + 1}}_{}^{} f (x) d x = {\int_{j}^{j + 1}}_{}^{} 1 \cdot f (x) d x

integrálra alkalmazzuk a parciális integrálás módszerét. Az azonosan 1 függvény

x + c

primitív függvényében a

c

állandó értékét válasszuk meg úgy, hogy

f (j + 1)

és

f (j)

szorzója megegyezzék:

\begin{matrix} {\int_{j}^{j + 1}}_{}^{} f (x) d x = {\int_{j}^{j + 1}}_{}^{} (x - j - \frac{1}{2})' f (x) d x = {[(x - j - \frac{1}{2}) f (x)]}_{j}^{j + 1} - \\ - {\int_{j}^{j + 1}}_{}^{} (x - j - \frac{1}{2}) f' (x) d x = \frac{1}{2} (f (j + 1) + f (j)) + \\ + {\int_{j}^{j + 1}}_{}^{} ([x] - x + \frac{1}{2}) \cdot f' (x) d x, \end{matrix}

hiszen a (

j, j + 1

) szakaszon

[x] = j

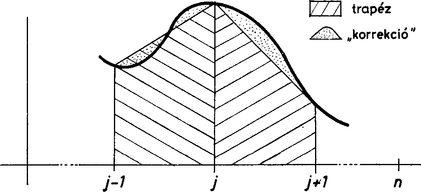1. ábra

Adjuk össze a

j = 0

1

...

(n - 1)

esetben kapott fenti egyenlőségeket, így

\begin{matrix} {\int_{0}^{n}}_{}^{} f (x) d x = \frac{1}{2} {\sum_{j = 0}^{n - 1}}_{}^{} (f (j + 1) + f (j)) + {\int_{0}^{n}}_{}^{} p (x) f' (x) d x \end{matrix}

adódik, ahol

p (x) = [x] - x + \frac{1}{2}

. Az integrál geometriai jelentése, mint tudjuk, a függvénygörbe és az

x

tengely közötti (előjeles) terület. A jobb oldalon álló összeg tagjai az 1. ábrán jelzett trapézok területét adják, maga a fenti formula pedig a numerikus integrálásban is jól ismert ún. trapéz-módszer képlete. A trapézösszegben az

f (0)

és

f (n)

értékek kivételével mindegyik

f (j)

függvényérték kétszer fordul elő, így eredményünket

\begin{matrix} {\int_{0}^{n}}_{}^{} f (x) d x = \frac{1}{2} [f (0) + f (n)] + \sum_{j = 1}^{n - 1} f (j) + {\int_{0}^{n}}_{}^{} p (x) f' (x) d x, \end{matrix}

illetve a

\begin{matrix} \begin{matrix} \sum_{j = 1}^{n} f (j) = {\int_{0}^{n}}_{}^{} f (x) d x + \frac{1}{2} [f (0) + f (n)] - {\int_{0}^{n}}_{}^{} p (x) f' (x) d x \end{matrix} \end{matrix}

(1)

alakba írhatjuk. Ez a nevezetes Euler‐féle összegképlet. A

0

és

n

egész számoknak nincs kitüntetett szerepe, gondolatmenetünk tetszőleges

a ≦ b

egész számokra a

\begin{matrix} \sum_{j = a}^{b} f (j) = {\int_{a}^{b}}_{}^{} f (x) d x + \frac{1}{2} [f (a) + f (b)] - {\int_{a}^{b}}_{}^{} p (x) f' (x) d x \end{matrix}

(2)

képletet adja.
Eredményünk alkalmazhatósága azon múlik, hogy ki tudjuk-e számítani az

{\int_{0}^{n}}_{}^{} f (x) d x

integrált és főleg, hogy tudjuk-e becsülni az

{\int_{0}^{n}}_{}^{} p (x) f' (x) d x

maradéktagot.

3. A harmonikus sor és az Euler‐állandó

Foglalkozzunk a bevezetőben felvetett egyik kérdéssel, az ún. harmonikus sor

s_{n} = 1 + \frac{1}{2} + ... + \frac{1}{n}

részletösszegeinek vizsgálatával. Alkalmazzuk Euler képletét az

f (x) = \frac{1}{x}

függvényre:

\begin{matrix} s_{n} = {\int_{1}^{n}}_{}^{} \frac{1}{x} d x + \frac{1}{2} (1 + \frac{1}{n}) + {\int_{1}^{n}}_{}^{} p (x) \frac{1}{x^{2}} d x = log n + \frac{1}{2} + \frac{1}{2 n} + {\int_{1}^{n}}_{}^{} p (x) \frac{1}{x^{2}} d x . \end{matrix}

{\int_{1}^{n}}_{}^{} p (x) \frac{1}{x^{2}} d x

maradéktagban újra a parciális integrálás módszerét akarjuk felhasználni. Vegyük ehhez szemügyre a

p (x) = [x] - x + \frac{1}{2}

függvényt. Ez a függvény 1 szerint periodikus, az egész számokban szakad és közöttük egyenes szakasz ábrázolja, mint az a 2. ábrán látható.

2. ábra

Ennek integrálfüggvényét, a

\begin{matrix} q (x) = {\int_{0}^{x}}_{}^{} p (t) d t \end{matrix}

függvényt a 3. ábra szemlélteti.

3. ábra

Mivel

{\int_{j}^{j + 1}}_{}^{} p (x) d x = 0

, ezért

q (x)

is 1 szerint periodikus és parabolaívekből áll (elsőfokú függvény integrálja másodfokú!). A definíció alapján azonnal látható, hogy

q ≧ 0

és

q (x) < max q (x) = q (\frac{1}{2}) = \frac{1}{8}

, továbbá

q (k) = 0

minden

k

egész szám esetén.
A parciális integrálás képlete szerint

\begin{matrix} {\int_{1}^{n}}_{}^{} p (x) \frac{1}{x^{2}} d x = {[q (x) \frac{1}{x^{2}}]}_{1}^{n} + 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x = 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x . \end{matrix}

Ennek alapján

\begin{matrix} s_{n} = log n + \frac{1}{2} + \frac{1}{2 n} + 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x, \end{matrix}

és itt már könnyű belátni, hogy a

\begin{matrix} {lim}_{n \to \infty}^{} 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x = 2 {\int_{1}^{\infty}}_{}^{} q (x) \frac{1}{x^{3}} d x \end{matrix}

határérték létezik. Valóban, a

2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x

sorozat (

n

, a felső határ a változó) monoton növekedő, mert

q (x) \frac{1}{x^{3}} > 0

és korlátos is, mert

\begin{matrix} 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x ≦ 2 {\int_{1}^{n}}_{}^{} \frac{1}{8} \cdot \frac{1}{x^{3}} d x = \frac{1}{4} {\int_{1}^{n}}_{}^{} \frac{1}{x^{3}} d x = \frac{1}{8} {[- \frac{1}{x^{2}}]}_{1}^{n} = \\ = \frac{1}{8} (1 - \frac{1}{n^{2}}) < \frac{1}{8} . \end{matrix}

Így persze a

γ = {lim}_{n \to \infty}^{} (\frac{1}{2} + \frac{1}{2 n} + 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x) = \frac{1}{2} + 2 {\int_{1}^{\infty}}_{}^{} q (x) \frac{1}{x^{3}} d x

határérték is létezik; ez a szám a nevezetes Euler-féle állandó. Igen sok helyen bukkan elő az analízisben, de ma sem ismeretes, hogy például

γ

racionális szám-e. Visszatérve

s_{n}

előállítására,

\begin{matrix} s_{n} = log n + \frac{1}{2} + \frac{1}{2 n} + 2 {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{3}} d x = log n + γ + \frac{1}{2 n} - 2 {\int_{n}^{\infty}}_{}^{} q (x) \frac{1}{x^{3}} d x, \end{matrix}

tehát

\begin{matrix} | s_{n} - log n - γ | ≦ \frac{1}{2 n} + 2 {\int_{n}^{\infty}}_{}^{} \frac{1}{8} \frac{1}{x^{3}} d x = \frac{1}{2 n} + \frac{1}{8 n^{2}}, \end{matrix}

vagyis

s_{n}

értéke igen jó közelítéssel

log n + γ

4. Az

n

! és a Stirling-formula

n

! tanulmányozásához térjünk át a

log (n!)

értékre. Persze

log (n!) = \sum_{k = 1}^{n} log k

, így most az

f (x) = log x

függvényre alkalmazzuk az Euler‐formulát:

\begin{matrix} \sum_{k = 1}^{n} log k = {\int_{1}^{n}}_{}^{} log x \end{matrix}

Itt

log x

integrálja könnyen meghatározható, mert

\begin{matrix} (x \end{matrix}

tehát a Newton‐Leibniz-formula szerint

\begin{matrix} \sum_{k = 1}^{n} log k = n log n - n + 1 + \frac{1}{2} log n - {\int_{1}^{n}}_{}^{} \frac{p (x)}{x} d x . \end{matrix}

Mint már az előző pontban is láttuk, parciális integrálással

\begin{matrix} - {\int_{1}^{n}}_{}^{} p (x) \frac{1}{x} d x = {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{2}} d x, \end{matrix}

és a jobb oldalon megint monoton növekedő korlátos sorozat áll, tehát létezik a

{lim}_{n \to \infty}^{} {\int_{1}^{n}}_{}^{} q (x) \frac{1}{x^{2}} d x = {\int_{1}^{\infty}}_{}^{} \frac{q (x)}{x^{2}} d x

véges határérték. Bevezetve a

K = 1 + {\int_{1}^{\infty}}_{}^{} q (x) \frac{1}{x^{2}} d x

jelölést, végül is a

\begin{matrix} log (n!) = \sum_{k = 1}^{n} log k = (n + \frac{1}{2}) log n - n + K - {\int_{n}^{\infty}}_{}^{} q (x) \frac{1}{x^{2}} d x \end{matrix}

képletre jutunk. Ebből

\begin{matrix} n! = \frac{n^{n}}{e^{n}} \sqrt[]{n} e^{k} \cdot e^{- {\int_{n}^{\infty}}_{}^{} \frac{q (x)}{x^{2}} d x} . \end{matrix}

Mivel itt

\begin{matrix} {\int_{n}^{\infty}}_{}^{} \frac{q (x)}{x^{2}} d x < \frac{1}{8} {\int_{n}^{\infty}}_{}^{} \frac{1}{x^{2}} d x = \frac{1}{8 n} \to 0, ha n \to \infty, \end{matrix}

ezért

\begin{matrix} e^{- {\int_{n}^{\infty}}_{}^{} q (x) \cdot \frac{1}{x^{2}} d x} \to 1, \end{matrix}

azaz

\begin{matrix} {lim}_{n \to \infty}^{}_{}^{} n! \frac{e^{n}}{n^{n} \sqrt[]{n} e^{K}} = 1. \end{matrix}

Ezt a tényt úgy fejezzük ki, hogy

n

! aszimptotikusan egyenlő az

\frac{n^{n}}{e^{n}} \sqrt[]{n} e^{K}

mennyiséggel.
A rejtélyes

e^{K}

állandó értéke kiszámítható, az eredmény a még rejtélyesebb:

\begin{matrix} e^{K} = \sqrt[]{2 π} \end{matrix}

összefüggés, de ennek részleteire most nem térünk ki.
Végül is a Stirling‐formula néven ismert

n! \approx \frac{n^{n}}{e^{n}} \sqrt[]{2 π n}

aszimptotikus egyenlőséget, vagy az

\begin{matrix} n! = \frac{n^{n}}{e^{n}} \sqrt[]{2 π n} e^{- {\int_{n}^{\infty}}_{}^{} q (x) \frac{1}{x^{2}} d x} \end{matrix}

pontos egyenlőséget kapjuk, ennek segítségével pedig

n

! igen jól és gyorsan számolható. Vegyük például a 100! számot. Zsebkalkulátorral is kiszámolható, hogy

\begin{matrix} e^{10} \approx 2, 718283^{10} \approx 2, 2 \cdot 10^{4} . \end{matrix}

Ezért

\begin{matrix} e^{100} \approx {(2, 2)}^{10} \cdot 10^{40} \approx 2, 6 \cdot 10^{43} . \end{matrix}

Ebből

\begin{matrix} \frac{100^{100}}{e^{100}} = \frac{10^{200}}{e^{100}} \approx \frac{10}{2,6} \cdot 10^{199 - 43} \approx 3, 8 \cdot 10^{156} . \end{matrix}

Végül

\begin{matrix} \sqrt[]{2 π 100} \cdot 3, 8 \cdot 10^{156} \approx 9, 6 \cdot 10^{157} . \end{matrix}

A 100! tehát 157 jegyű szám a 10-es számrendszerben.

5. Hatványösszegek vizsgálata

Foglalkozzunk végül azzal a kérdéssel, hogyan összegezhetjük pozitív egész számok hatványait. Ha a

\sum_{k = 1}^{n} k

összeg meghatározásakor alkalmazzuk Euler képletét az

f (x) = x

függvényre, akkor nyilván

\begin{matrix} \sum_{k = 1}^{n} k = \sum_{k = 0}^{n} k = {\int_{0}^{n}}_{}^{} x d x + \frac{1}{2} n - {\int_{0}^{n}}_{}^{} p (x) d x = \frac{n^{2}}{2} + \frac{n}{2} = \frac{n (n + 1)}{2} . \end{matrix}

Az eredmény közismert, mint ahogyan a négyzetek összegére vonatkozó formula is az, de lássuk megint, hogyan működik a módszer:

\begin{matrix} \sum_{k = 1}^{n} k^{2} = \sum_{k = 0}^{n} k^{2} = {\int_{0}^{n}}_{}^{} x^{2} d x + \frac{1}{2} n^{2} - {\int_{0}^{n}}_{}^{} p (x) 2 x d x = \frac{n^{3}}{3} + \frac{1}{2} n^{2} + {\int_{0}^{n}}_{}^{} q (x) \cdot 2 d x = \\ = \frac{n^{3}}{3} + \frac{1}{2} n^{2} + 2 n {\int_{0}^{1}}_{}^{} q (x) d x . \end{matrix}

Definíció szerint

q (x) = {\int_{0}^{x}}_{}^{} ([t] - t + \frac{1}{2}) d t

és így

0 ≦ x ≦ 1

esetén

\begin{matrix} q (x) = {\int_{0}^{x}}_{}^{} (\frac{1}{2} - t) d t = {[\frac{1}{2} t - \frac{1}{2} t^{2}]}_{0}^{x} = \frac{1}{2} (x - x^{2}), \end{matrix}

tehát

\begin{matrix} {\int_{0}^{1}}_{}^{} q (x) d x = {\int_{0}^{1}}_{}^{} \frac{1}{2} (x - x^{2}) d x = {[\frac{x^{2}}{4} - \frac{x^{3}}{6}]}_{0}^{1} = \frac{1}{4} - \frac{1}{6} = \frac{1}{12} . \end{matrix}

Ezt visszahelyettesítve

\begin{matrix} \sum_{k = 1}^{n} k^{2} = \frac{n^{3}}{3} + \frac{n^{2}}{2} + \frac{n}{6} = \frac{2 n^{3} + 3 n^{2} + n}{6} = \frac{n (n + 1) (2 n + 1)}{6} . \end{matrix}

Az Euler-képlet előnye itt az elemi megfontolásokkal szemben elsősorban az, hogy módszeresen vezet el a kívánt összegek kiszámításához, így elvárható, hogy pl. az 5-ik hatványok összegét, a

\sum_{k = 1}^{n} k^{5}

számot is meghatározhatjuk vele:

\begin{matrix} \sum_{k = 1}^{n} k^{5} = \sum_{k = 0}^{n} k^{5} = {\int_{0}^{n}}_{}^{} x^{5} d x + \frac{1}{2} n^{5} - {\int_{0}^{n}}_{}^{} p (x) \cdot 5 x^{4} d x . \end{matrix}

Hogyan számítsuk most ki az

{\int_{0}^{n}}_{}^{} p (x) 5 x^{4} d x

maradéktagot? A

\sum_{k = 1}^{n} k

összegnél a maradéktag zérus volt, a

\sum_{k = 1}^{n} k^{2}

összegnél pedig ‐ a már korábban is bevált ‐ parciális integrálást alkalmaztuk. Ezt tesszük a továbbiakban is, ismételt parciális integrálással megszabadítjuk az integrált az

x^{4}

tényezőtől. Ehhez célszerű lesz a

p

függvény számára egy eltolt integrálfüggvényt választani. A

q (x) = \int_{0}^{x}_{}^{} p (t) d t

függvény ugyanis nem örökli a

p

azon tulajdonságát, hogy a tengely feletti és a tengely alatti részei kiegyenlítik egymást és így

{\int_{0}^{1}}_{}^{} p (x) d x = 0

. Fentebb már láttuk, hogy

{\int_{0}^{1}}_{}^{} q (x) d x = \frac{1}{12}

. Módosítsuk

q

-t, vezessük be a

p_{2} (x) = q (x) - \frac{1}{12}

függvényt. Ekkor még mindig igaz (a (0, 1) intervallumon) a

p_{2}^{'} (x) = p (x)

összefüggés és persze

{\int_{0}^{1}}_{}^{} p_{2} (x) d x = 0

Folytassuk ezt az eljárást, definiáljuk rekurzióval a

\begin{matrix} p_{1} (x), p_{2} (x), ..., p_{n} (x), ... (0 ≦ x ≦ 1) \end{matrix}

függvénysorozatot a következő módon.
Legyen

p_{1} = p

p_{2} = q - \frac{1}{12}

, és általában, ha

p_{n}

már definiált (

n ≧ 0

), akkor legyen

p_{n + 1}

olyan függvény, amelyre

\begin{matrix} p'_{n + 1} (x) = p_{n} (x) (0 ≦ x ≦ 1) \end{matrix}

és

\begin{matrix} {\int_{0}^{1}}_{}^{} p_{n + 1} (x) d x = 0. \end{matrix}

E két feltétel egyértelműen meghatározza a

p_{n + 1}

függvényt. Jegyezzük meg, hogy a

q_{n + 1} (x) = {\int_{0}^{x}}_{}^{} p_{n} (t) d t

integrálfüggvénnyel kifejezve

\begin{matrix} p_{n + 1} (x) = q_{n + 1} (x) - {\int_{0}^{1}}_{}^{} q_{n + 1} (x) d x . \end{matrix}

Teljes indukcióval azonnal világos, hogy

p_{n}

n

-edfokú polinom [0, 1]-en és mivel

\begin{matrix} 0 = {\int_{0}^{1}}_{}^{} p_{n - 1} (x) d x = p_{n} (1) - p_{n} (0), (n ≧ 2) \end{matrix}

ezért

p_{n} (1) = p_{n} (0) (n ≧ 2)

. Így aztán mindegyik

p_{n}

(

n ≧ 2

) folytonosan és periodikusan kiterjeszthető az egész számegyenesre.
Az imént definiált

p_{n}

függvények az ún. Bernoulli‐polinomok (bár csupán a [0, 1] szakaszon polinomok). Számítsuk ki a sorozat néhány tagját. Láttuk,

0 ≦ x ≦ 1

esetén

\begin{matrix} p_{1} (x) = - x + \frac{1}{2}, p_{2} (x) = - \frac{1}{2} x^{2} + \frac{1}{2} x - \frac{1}{12} . \end{matrix}

Ekkor

\begin{matrix} p_{3} (x) = - \frac{1}{6} x^{3} + \frac{1}{4} x^{2} - \frac{1}{12} x + c \end{matrix}

és

\begin{matrix} 0 = {\int_{0}^{1}}_{}^{} p_{3} (x) d x = {[- \frac{x^{4}}{24} + \frac{x^{3}}{12} - \frac{x^{2}}{24} + c x]}_{0}^{1} = c, \end{matrix}

tehát

\begin{matrix} p_{3} (x) = - \frac{1}{6} x^{3} + \frac{1}{4} x^{2} - \frac{1}{12} x . \end{matrix}

Ezután

\begin{matrix} p_{4} (x) = - \frac{1}{24} x^{4} + \frac{1}{12} x^{3} - \frac{1}{24} x^{2} + c \end{matrix}

és

\begin{matrix} 0 = {\int_{0}^{1}}_{}^{} p_{4} (x) d x = {[- \frac{1}{120} x^{5} + \frac{1}{48} x^{4} - \frac{1}{72} x^{3} + c x]}_{0}^{1} = - \frac{1}{120} + \frac{1}{48} - \frac{1}{72} + c, \end{matrix}

tehát

\begin{matrix} c = \frac{6 - 15 + 10}{720} = \frac{1}{720}, \end{matrix}

és így

\begin{matrix} p_{4} (x) = - \frac{1}{24} x^{4} + \frac{1}{12} x^{3} - \frac{1}{24} x^{2} + \frac{1}{720} . \end{matrix}

Még egy lépéssel továbbhaladva

\begin{matrix} p_{5} (x) = - \frac{1}{120} x^{5} + \frac{1}{48} x^{4} - \frac{1}{72} x^{3} + \frac{1}{720} x + c, \\ 0 = {\int_{0}^{1}}_{}^{} p_{5} (x) d x = {[- \frac{1}{720} x^{6} + \frac{1}{240} x^{5} - \frac{1}{288} x^{4} + \frac{1}{1440} x^{2} + c x]}_{0}^{1} = \\ = \frac{- 2 + 6 - 5 + 1}{1440} + c = c, \end{matrix}

tehát

\begin{matrix} p_{5} (x) = - \frac{1}{120} x^{5} + \frac{1}{48} x^{4} - \frac{1}{72} x^{3} + \frac{1}{720} x . \end{matrix}

Észrevehetjük, hogy

p_{3}

és

p_{5}

konstans tagja zérus, és teljes indukcióval igazolható, hogy ez minden páratlan indexű Bernoulli-polinomra igaz (az

n = 1

eset kivételével), azaz

p_{2 n + 1} (0) = p_{2 n + 1} (1) = 0 (n = 1, 2, ...)

. Ebből a periodikus kiterjesztés miatt a

p_{2 n + 1} (k) = 0

bármely

k

egész számra. Térjünk most már vissza az

{\int_{0}^{n}}_{}^{} p (x) 5 x^{4} d x

integrál kiszámítására.

\begin{matrix} 5 {\int_{0}^{n}}_{}^{} p (x) x^{4} d x = 5 {\int_{0}^{n}}_{}^{} p_{1} (x) x^{4} d x = 5 {[p_{2} (x) x^{4}]}_{0}^{n} - 5 \cdot 4 \cdot {\int_{0}^{n}}_{}^{} p_{2} (x) x^{3} d x = \\ = - \frac{5}{12} n^{4} - 20 {\int_{0}^{n}}_{}^{} p_{2} (x) x^{3} d x, \end{matrix}

hiszen

p_{2} (0) = p_{2} (1) = ... = p_{2} (n) = - \frac{1}{12}

a periodikus kiterjesztés miatt. Folytassuk a parciális integrálást:

\begin{matrix} - 20 {\int_{0}^{n}}_{}^{} p_{2} (x) x^{3} d x = - 20 {[p_{3} (x) x^{3}]}_{0}^{n} - (- 20) \cdot 3 {\int_{0}^{n}}_{}^{} p_{3} (x) x^{2} d x = \\ = 60 {\int_{0}^{n}}_{}^{} p_{3} (x) x^{2} d x, \end{matrix}

hiszen

p_{3} (0) = p_{3} (1) = ... = p_{3} (n) = 0

. Ismét parciális integrálással

\begin{matrix} 60 {\int_{0}^{n}}_{}^{} p_{3} (x) x^{2} d x = 60 {[p_{4} (x) x^{2}]}_{0}^{n} - 60 \cdot 2 {\int_{0}^{n}}_{}^{} p_{4} (x) x d x = \\ = 60 {[p_{4} (x) x^{2}]}_{0}^{n} - 60 \cdot 2 \cdot {[p_{5} (x) x]}_{0}^{n} + 60 \cdot 2 \cdot {\int_{0}^{n}}_{}^{} p_{5} (x) d x = 60 p_{4} (n) n^{2} = \frac{60}{720} n^{2}, \end{matrix}

hiszen

\begin{matrix} p_{4} (n) = p_{4} (0) = \frac{1}{720} és p_{5} (n) = p_{5} (0) = 0. \end{matrix}

Végül azt kapjuk, hogy

\begin{matrix} 5 {\int_{0}^{n}}_{}^{} p (x) x^{4} d x = - \frac{5}{12} n^{4} + \frac{1}{12} n^{2}, \end{matrix}

tehát

\begin{matrix} \sum_{k = 0}^{n} k^{5} = {\int_{0}^{n}}_{}^{} x^{5} d x + \frac{1}{2} n^{5} - {\int_{0}^{n}}_{}^{} p (x) 5 x^{4} d x = \frac{n^{6}}{6} + \frac{1}{2} n^{5} + \frac{5}{12} n^{4} - \frac{1}{12} n^{2} = \\ = \frac{2 n^{6} + 6 n^{5} + 5 n^{4} - n^{2}}{12} = \frac{n^{2} {(n + 1)}^{2} (2 n^{2} + + 2 n - 1)}{12} \end{matrix}

lesz a keresett összegző formula.

A fenti példán már jól látszik az általános módszer: A

\sum_{k = 1}^{n} k^{j}

összeg kiszámításához fel kell írni a

p_{1} (x), ..., p_{j} (x)

Bernoulli polinomokat és az

{\int_{0}^{n}}_{}^{} p (x) j x^{j - 1} d x

integrál ismételt parciális integrálással a

p_{i} (n)

számok ismeretében könnyen meghatározható.
Természetesen az ismételt parciális integrálással adódó képlet az

{\int_{0}^{n}}_{}^{} p (x) f' (x) d x

általános esetre is felírható (ha

f

kellően sokszor differenciálható), és így az Euler-képlet finomított alakjához jutunk, melyben a maradéktag

{\int_{0}^{n}}_{}^{} p_{k} (x) f^{(k)} (x) d x

alakú integrál lesz. Ezeket a képleteket már nem írjuk le (az olvasó maga könnyen megteheti), most csupán megemlítjük, hogy mind az Euler-képlet (1) alatti alapesetének, mind pedig a finomított változatnak igen sok további érdekes alkalmazása van.