Cím:	Számok a valóson innen és túl (2) (fordította Virágh János)
Szerző(k):	Knuth, Donald E.
Füzet:	1987/május, 193 - 196. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 2. Szimbólumok   A: Bill, azt hiszem, a te Conway Kövednek mégis van valami értelme. Gondolkodtam rajta az éjjel. B: Én is, csak elszundítottam, mielőtt valamire jutottam volna. Mi a rejtély kulcsa? A: Igazán nem olyan nehéz. Csak az zavar, hogy minden szavakkal van kifejezve. Ugyanezt le lehet írni jelekkel, és akkor rögtön látod, miről van szó. B: Azt mondod, most meg az új matekot használjuk föl ennek a régi kőtáblának a megfejtésére? A: Nem szívesen ismerem be, de körülbelül ez a helyzet. Az első szabály itt azt mondja ki, hogy minden $x$ szám valójában az $x_B$ bal oldali halmazból és az $x_j$ jobb oldali halmazból álló rendezett halmazpár: $\begin{array}{c}{\displaystyle x=\left(x_B\mathrm{,}{x}_J\right)\mathrm{.}}\end{array}$ B: Várj csak, nem muszáj a homokba írnod. A hátizsákomban alighanem van még egy ceruza és valamennyi papír. Egy pillanat $\text{...}$ Tessék! A: $\begin{array}{c}{\displaystyle x=\left(x_B\mathrm{,}{x}_J\right)\mathrm{.}}\end{array}$ $x_B$ és $x_j$ nem igazi szám, hanem számokból álló halmaz. A halmaz minden eleme újra egy rendezett halmazpár, és így tovább. B: Várj egy kicsit, összezavarodtam a jelöléseidtől. Nem tudom, mi szám és mi halmaz. A: Jó, ezután kis betűvel jelölöm a számokat, naggyal pedig a számokból álló halmazokat. Conway első szabálya azt mondja, hogy $\begin{array}{c}{\displaystyle x=\left(X_B\mathrm{,}{X}_J\right)\mathrm{,}\text{ahol}{X}_B/\geqq X_J\mathrm{.}}\end{array}$ (1) Ez azt jelenti, hogy ha $x_B$ az $X_B$ halmazból való tetszőleges szám és az $x_j$ szám az $X_j$ tetszőleges eleme, akkor $x_B/\geqq x_J\mathrm{.}$ Vagyis $x_B$ nem lehet nagyobb vagy egyenlő, mint $x_J\mathrm{.}$ B: (fejét vakarja) Attól tartok, még mindig túl gyorsan magyarázod. Ne felejtsd el, hogy te már megemésztetted ezt a dolgot, én meg még csak az elején vagyok. Ha minden szám egy rendezett halmazpár, és ezek a halmazok megint csak számokból, vagyis rendezett halmazpárokból állnak, és így tovább, akkor hogy lehetett ezt az egészet elkezdeni? A: Jó kérdés! Pont ez a csodálatos a Conway-féle sémában. $X_B$ és $X_J$ minden elemét már előzőleg meg kell teremteni. Ámde a teremtés első napján még nincsenek olyan előzőleg teremtett számok, amelyeket fölhasználhatnánk. Így $x_B$-nek is, meg $x_J$-nek is az üres halmazt kell vennünk! B: Soha nem gondoltam volna, hogy egyszer megtudom, néha az üres halmaznak is van értelme. Ez tényleg olyasmi, mintha a semmiből teremtenénk valamit, nem? De igaz-e $X_B\geqq X_J\mathrm{,}$ ha mindkettő az üres halmaz? Hogyan lehet valami nem egyenlő saját magával? Ja persze, ez rendben van, hiszen csak annyit jelent, hogy az üres halmaz egyetlen eleme sem nagyobb vagy egyenlő az üres halmaz valamely eleménél, ez meg igaz állítás, hiszen az üres halmaznak nincsenek elemei. A: Így szabályosan elkezdődött minden, és megkaptuk a nullának nevezett számot. Ha az üres halmazt $\varnothing$-val jelöljük, $\begin{array}{c}{\displaystyle 0=\left(\varnothing \mathrm{,}\varnothing \right)\mathrm{.}}\end{array}$ B: Hihetetlen! A: második napon már használhatjuk a 0-t a bal vagy a jobb oldali halmazban. Ezért kap Conway két további számot: $\begin{array}{c}{\displaystyle -1=\left(\varnothing \mathrm{,}\left\{0\right\}\right)\text{és}1=\left(\left\{0\right\}\mathrm{,}\varnothing \right)\mathrm{.}}\end{array}$ B: Nézzük csak, megy ez így? Ahhoz, hogy a $-1$ szám legyen, annak kell teljesülni, hogy az üres halmaz egyetlen eleme se legyen nagyobb vagy egyenlő mint $0.$ És hogy az $1$ szám legyen, ahhoz az kell, hogy $0$ ne legyen nagyobb vagy egyenlő az üres halmaz egyetlen eleménél sem. Te, ez az üres halmaz biztos híres lesz egyszer. Azt hiszem, írni fogok egy könyvet Az üres halmaz tulajdonságai címmel. A: Soha nem fejeznéd be. Ha $X_B$ vagy $X_J$ az üres halmaz, az $X_B/\geqq X_J$ feltétel mindig teljesül, függetlenül attól, hogy mi a másik halmaz. Ez azt jelenti, hogy végtelen sok számot teremthetünk. B: Jó, de mi van Conway második szabályával? A: Azzal akkor tudjuk megmondani, hogy igaz-e $X_B/\geqq X_J\mathrm{,}$ ha egyik halmaz sem üres. Az a szabály definiálja a ''kisebb vagy egyenlő''-t. Jelekkel fölírva: $\begin{array}{c}{\displaystyle x\leqq y\text{ha}{X}_B\geqq y\text{és}x\geqq Y_J}\end{array}$ (2) B: Várj csak, megint nagyon előreszaladtál. Nézd, $X_B$ számokból álló halmaz, $y$ meg szám, vagyis halmazokból álló rendezett pár. Mit értesz azon, hogy $X_B/\geqq y?$ A: Azt, hogy $X_B$ minden $x_B$ elemére teljesül $x_B/\geqq y$. Másképpen szólva, $X_B$ egyetlen eleme sem nagyobb vagy egyenlő, mint $y$. B: Értem! A te (2) szabályod még megköveteli azt is, hogy $x$ nem nagyobb vagy egyenlő $Y_J$ egyetlen eleménél sem. Hadd hasonlítsam össze a szöveggel... A: A Kövön kicsit másképpen van, de $x\leqq y$ biztos ugyanaz, mint $y\geqq x\mathrm{.}$ B: Igen, igazad van. Te, várj csak, nézd itt oldalt ezeket a véseteket: 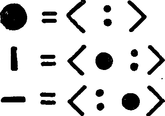    Ezt nem tudtam tegnap megfejteni. Most a te jelöléseddel minden világos! A kettőspontok választják el a bal oldali halmazt a jobb oldali halmaztól. Biztos jó nyomon vagy. A: Hűha, egyenlőségjelek, meg minden! Az a kőkorszaki vésnök biztos ,,‐''-t írt a $-1$ helyett. Nekem majdnem jobban tetszik az ő jelölése, mint az enyém. B: Biztos vagyok benne, hogy túlságosan lebecsüljük a primitív népeket. Pedig ők is bizonyára színes életet élnek, és épp úgy szükségük van agytornára is, mint nekünk. Ha éppen nem kell élelemért vagy menedékért küzdeniük. Visszatekintve általában túl egyszerűnek látjuk a történelmet. A: Ez igaz, de hogyan tudnánk másképpen visszanézni? B: Értem, mire gondolsz. A: Most következik az a része a szövegnek, amit nem tudok felfogni. Conway ,,bebizonyítja'' a teremtés első napján, hogy $0\leqq 0.$ Miért kell azzal bajlódnia, hogy belássa, hogy valami kisebb vagy egyenlő saját magával, mikor nyilván egyenlő saját magával. Aztán a második napon azt ,,bizonyítja'', hogy $-1$ nem egyenlő $0$-val. Nem nyilvánvaló ez bizonyítás nélkül is? Hiszen a $-1$ egy másik szám ! B: Hm. Nem tudom, te hogy vagy vele, én szívesen úsznék újra egyet. A: Nagyszerű ötlet. Nem vagyok hozzászokva, hogy ilyen sokáig koncentráljak. Az a tajtékos partrész jónak látszik. Menjünk!  Fordította : Virágh János   $\begin{array}{c}{\displaystyle *}\end{array}$   Ezen a ponton el kell válnunk hőseinktől, akik a Gondolat Könyvkiadó gondozásában a nem túl távoli jövőben megjelenő könyv további fejezeteiben megkísérlik földeríteni, hogy a két törvény nyomán hogyan teremthetők meg mind a ,,számok a valóson innen és túl''. Az első napon tehát a $0$, a másodikon a $-1$ és az $1$, azután pedig a harmadik napon az $1/2$, a $2$, a $-1/2$ és a $-2$ teremtésére kerül sor. Kiderül például, hogy $\frac{1}{2}=\left(\mathrm{0,1}\right)=\left(\left\{-\mathrm{1,0}\right\}\mathrm{,1}\right)$. A számoknak tehát több alakja van, Alice és Bill azonban megtalálják ezek legegyszerűbbikét. Megtudjuk, hogy bármely $y$ számra igaz, hogy ha $x$ az elsőként teremtett olyan szám, amelyre Persze két szám egyenlősége most definiált reláció, $x=y$, ha $x\le y$ és $y\le x$. Az $n$-edik napon, amikor valamennyi addig megteremtett szám felhasználható bal és jobb oldali halmazok készítésére, $2^{n-1}$ darab új szám jön létre; mindegyikük szép rendben illeszkedik két, korábban már megteremtett szám közé. Eközben hőseink bebizonyítják ‐ teljes indukcióval ‐ hogy a $\le$ reláció tranzitív, továbbá hogy egy $x=\left(X_B\mathrm{,}{X}_J\right)$ szám ,,elválasztja'' egymástól a bal és a jobb oldali halmazát, azaz $X_B\le x$ és $x\le X_J$. Belátják, hogy bármely két szám összehasonlítható, azaz vagy $x\le y$, vagy $y\le x$ . Rábukkannak a kő további részére is, ahol a számokkal végzett műveletek leírása olvasható. Eszerint $\begin{array}{c}{\displaystyle x+y=\left(\left(X_B+y\right)\cup \left(Y_B+x\right)\mathrm{,}\left(Y_J+x\right)\cup \left(X_J+y\right)\right)\mathrm{,}}\end{array}$ illetve $\begin{array}{c}{\displaystyle -x=\left(-X_J\mathrm{,}-X_B\right)\mathrm{.}}\end{array}$ Ellenőrizhetik, hogy pl. $\frac{1}{2}+\frac{1}{2}$ valóban $1$, és hogy az összeadás általában rendelkezik a jól ismert tulajdonságokkal. Kezdetben persze ‐ ugyancsak indukcióval ‐ be kell látniuk, hogy a fenti definíciók is számokat határoznak meg. Az idő pedig egyre gyorsabban telik : a ,,végtelenedik napon'' először kerülhet sor arra, hogy $X_B$ vagy $X_J$ végtelen halmaz legyen. És ezen a ,,végtelenedik napon'' létrejönnek mind a valós számok, sőt olyan különös számok is, mint $\begin{array}{c}{\displaystyle \left(\mathrm{0,}\left\{\mathrm{1,}\frac{1}{2}\mathrm{,}\frac{1}{4}\mathrm{,}\text{...}\right\}\right)\mathrm{,}}\end{array}$ amely nagyobb 0-nál, de minden pozitív valós számnál kisebb. A teremtésnek pedig még mindig nincs vége...   $\begin{array}{c}{\displaystyle *}\end{array}$   Nos az Olvasóra hagyjuk, folytassa a két felfedező munkáját.