Cím: A számítógépről, avagy a matematikusok bal kezéről
Szerző(k):  Kós Géza 
Füzet: 1987/március, 97. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Sokszor kerülünk olyan helyzetbe, hogy egy matematikai állítás helyességét vagy helytelenségét nem tudjuk közvetlenül bizonyítani. Ilyen esetekben legtöbbször az állítás speciális eseteit vizsgálva próbálunk közelebb jutni a megoldáshoz. Bizonyos feladatfajták esetében nagy segítséget nyújthat a számítógép, amely sebessége révé töredékére csökkentheti a felhasználandó időt, mindössze a megfelelő programot kell megírni. Nézzük ezt egy konkrét feladat kapcsán!

 

Milyen pozitív egész n-ekre lehet az 1,  2, ...,  3n-1,3n számokat n csoportba osztani úgy, hogy minden csoportban három szám legyen, s a három szám közül a legnagyobb egyenlő legyen a másik kettő összegével?
 

Egy ilyen felosztás létezéséhez szükséges, hogy a számok összege páros legyen. Valóban, a számok összege minden egyes csoportban a legnagyobb szám kétszeresével egyenlő, tehát páros, és így az összes csoportban levő számok összege is az.
Könnyen ellenőrizhető, hogy
1+2+...+3n=3n(3n+1)2
pontosan akkor páros, ha n 4-gyel osztva 0 vagy 1 maradékot ad. A feltétel tehát a következő :
 
Ahhoz, hogy a számokat a feltételeknek megfelelően feloszthassuk, szükséges, hogy n 4-gyel osztva 0 vagy 1 maradékot adjon
 

Ez a feltétel sok n-re kizárja a felosztás létezését; de mi a helyzet a többi esetben? n=1-re a felosztás magától adódik : 1+2=3. n=4-re és n=5-re is viszonylag könnyű megfelelő felosztásokat találni, például
 
  1,11,12  1,14,15    2,  7,  92,10,12    3,  5,  83,6,  9    4,  6,104,  7,11  5,  8,13.  

 
Számítógép segítségével nagyobb n-ekre is kereshetünk megoldást. Ehhez egy algoritmusra van szükségünk, amely valamilyen módon hármas csoportokat keres az 1, 2, ..., 3n számok között, és ahol több lehetőség közül választhat, ott minden esetet végigvizsgál valamilyen módszer szerint. Programunk tehát valójában egy fát vizsgál végig, amelyen az ágak a kialakítható számhármasokat, a csomópontok pedig a választási lehetőségeket jelölik (1. ábra).
 
 
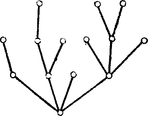1. ábra
 

Minden egyes csomóponthoz egyértelműen hozzárendelhetők azok az ágak, amelyeken eljuthatunk hozzá a kezdőpontból; minden csomóponthoz tartozik tehát egy ,,megkezdett'' felosztás, a pontból kiinduló ágak pedig a lehetséges folytatások. (Ha a felosztást nem lehet folytatni, a csomópontból nem indul ki egy ág sem.)
Természetesen nem szükséges az összes lehetséges ágnak kiindulnia a csomópontból: elegendő néhány olyat kiválasztani, amelyek közül valamelyik biztosan szerepel a teljes felosztásban. Például a kezdőpontban elegendő azokat figyelembe venni, amelyekhez tartozó számhármasban az 1-es előfordul; ezeknek a száma mindössze 3n-2.
Korlátozzuk tehát az egyes csomópontokból kiinduló ágak számát úgy, hogy az ágakhoz tartozó számhármasok legkisebb elemei egyenlőek legyenek a legkisebb pozitív egésszel, amely a csomóponthoz tartozó részfelosztásban még nem szerepel. Ha a csomóponthoz tartozó részfelosztást be lehet fejezni, akkor mindenképpen szerepelnie kell ilyen számhármasnak. Az ily módon felépített fában az összes megoldás megtalálható.
Azt kell még eldöntenünk, hogyan járja végig programunk a fát. Minden csomópontban valahogy sorbarendezzük az ágakat, majd az elsőnek választott ágon ,,lejjebb'' lépünk. Ha ezzel programunk teljes felosztást kap, azt kinyomtatja és leáll. Ha elakad, visszalép az előző csomóponthoz, és az onnan kiinduló ágak közül a rendezés szerinti rákövetkezőn próbálkozik (2. ábra). Ha a kezdőpontban ,,akad el'', az azt jelenti, hogy már az egész fát végigjárta és nem talált megoldást.
 
 
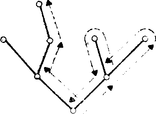2. ábra
 

Az ágak sorbarendezése történhet például a középső elem szerint, az első ág legyen mondjuk az, amelyhez a legkisebb középső érték tartozik. A program persze nem építi fel egyszerre az egész fát; mindig csak azokat az éleket ‐ illetve a hozzájuk tartozó számhármasokat ‐ jegyzi meg, amelyeken az éppen vizsgált csomópontba lehet eljutni.
 
 
3. ábra
 

A pillanatnyi részfelosztást, vagyis azokat az éleket, amelyeken az éppen vizsgált csomópontba lehet eljutni, három n elemű tömbben fogjuk tárolni. A(i) az i-edik számhármas legkisebb, B(i) a középső, C(i) pedig a legnagyobb elemét tartalmazza. A számhármasok (élek) számát K fogja jelölni.
 
1. program
 

  10  DEFINT A‐Z  330  IF K=N THEN 600  20  IMPUT "N=";N  340  L=L+1:IF V(L)=1 THEN 340  30  N3=3*N    350  GO TO 100  40  DIM A(N),B(N),C(N),V(N3)  50  K=0:L=1    400  IF K=0 THEN 500  410  L=A(K):M=B(K)  100  M=L    420  V(L)=0:V(M)=0:V(L+M)=0  200  M=M+1  430  K=K-1  210  IF L+M>N3 THEN 400    440  GO TO 200  220  IF V(M)=1 OR V(L+M)=1  THEN 200    500  PRINT "NINCS MEGOLDÁS"  510  END  300  K=K+1    600  FOR I=1 TO N  310  A(K)=L:B(K)=M:C(K)=L+M    610  PRINT A(I); B(I); C(I)  320  V(L)=1:V(M)=1:V(L+M)=1    620  NEXT  I  630  END

 

A gyorsabb futás érdekében még egy 3n elemű V tömböt is használunk, amelynek elemei azt mutatják, milyen számok szerepelnek a már meglevő hármas csoportokban : ha V(i)=0, akkor i még nem szerepel, ha V(i)=1, akkor i már szerepel. A legkisebb számot, amelyet még nem használtunk fel, L jelöli.
A program működését az algoritmus ismeretében nem nehéz megérteni. A 10‐50. sorokban a változók kapnak kezdőértéket (az N3 változó 3n-et tartalmazza, hogy ezt ne kelljen újra meg újra kiszámítani). A 100. sorban kezdődik el egy új csomópont vizsgálata. A soron következő ágat a 200‐220. sorokban keressük (a számhármas legkisebb eleme az algoritmus szerint L, a következő pedig M ); ha nincs további ág, a 400. sorra ugrunk.
A 300‐350. sorokban az új ágon a következő csomópontra lépünk, s ennek megfelelően módosítjuk K és L értékét, valamint a tömbök tartalmát. Ha ezzel teljes felosztást kaptunk, azt a 600. sorban nyomtatjuk ki.
A 400‐440. sorokra akkor kerül sor, ha egy csomópontban nincs több ág. Ha ez a kezdőpont (K=0), akkor ez azt jelenti, hogy a program végigjárta a fát és nem talált megoldást. Ellenkező esetben visszalépünk az előző csomópontra és a 200. sortól a következő ágat kezdjük vizsgálni. Futtassuk a programot! Észrevehetjük, hogy n növekedtével a futási idő rohamosan nő:
 
n    1    2    3    4    5    6    7  futási idő másodpercben<1   <1     4    7    38    1359    ?
 


s problémánkról mindeddig nem nyertünk új információt. Hogyan lehet az algoritmust módosítani ahhoz, hogy a program gyorsabb legyen?
Indítsuk el a programot valamilyen nagyobb értékkel, mondjuk n=10-zel. Egy-két perc után szakítsuk meg a program futását és nyomtassuk ki a V tömböt az alábbi sorral;
 
FOR I=1 TO N3:PRINT V(I); :NEXT I
 

Észrevehetjük, hogy a program főleg a kis számokat használta fel, a nagyok majdnem mind megmaradtak, pedig azokat nagyon kényelmetlen kezelni. Gondoljuk csak meg : minden számhármasban a legkisebb szám kisebb, mint a legnagyobb fele, a program viszont a számok ,,kisebbik felét'' majdnem teljesen felhasználta. Az algoritmus túlságosan mohó : hamar építi be őket a hármas csoportokba.
Módosítsuk tehát az algoritmust úgy, hogy először a nagy számokat használja fel. Az új fa mindössze egy dologban különbözik a régitől: most az egyes csomópontokból kiinduló élek kiválasztásakor a számhármasnak ne a legkisebb, hanem a legnagyobb elemét rögzítsük. Így a kisebb számok maradnak meg a későbbi csoportok számára.
 
2. program
 

  10  DEFINT A‐Z  330  IF K=N THEN 600    20  INPUT "N="; N  340  L=L‐1:IF (VL)=1 THEN 340    30  N3=3*N  350  GO TO 100  40  DIM A(N), B(N), C(N),V(N3)  400  IF K=0 THEN 500  50  K=0:L=N3  410  L =C(K):M =A(K)420  V(M)=0:V(L‐M)=0:V(L)=0  100  M=0  430  K =K‐1  200  M =M +1    440  GO TO 200  210  IF M > = L‐M THEN 400  500  PRINT "NINCS MEGOLDÁS"  220  IF V(M) =1 OR V(L‐M)=1  510  ENDTHEN 200600  FOR I=1 TO N  300    K =K+ I  610  PRINT A(I); B(I) ; C(I)    310    A(K) = M : B(K)= L‐M : C(K) = L  620  NEXT I    320  V(M) =1: V(L‐M) =1: V(L) =1  630  END
 

A program nem sokban változott; L most a legnagyobb még nem felhasznált számot jelöli, M pedig az új számhármas legkisebb elemét. Azt tapasztaljuk, hogy a programunk gyorsabb:
 
n123456789  futási idő másodpercben<1<1213260?53167
 


n=8 és n=9-re a program egy-egy megfelelő felosztást írt ki; ezekre tehát igazoltuk az alábbi sejtést:
 
Ha n néggyel osztva 0 vagy 1 maradékot ad, az 1,2,...,3n-1,3n számok beoszthatók n darab hármas csoportba úgy, hogy minden csoportban az egyik elem egyenlő legyen a másik kettő összegével.
 

A sebességnövekedésnek más oka is van. Az új fa felépítésével egy sor felesleges ágtól megszabadultunk.
 
n    1    2    3    4    5    6    7    8    9    10  1. program  1    4    20    122    776    5564    46 162    435 082    4 567 651    52 248 466    2. program  1    2    10    48    212    1018    6 546    47 973    379 777    3 054 273  
Az élek száma
 

Látható, hogy az első fa sokkal több ágat tartalmaz, mint a második. Ez érthető is, hiszen a második fán ‐ főleg a fa felső részein ‐ egy csomópontból kb. feleannyi ág indul ki, mint az elsőn, hiszen az elsőn adott különbségű, a másodikban adott összegű elemeket keresünk.
A fák alsó részein levő csomópontokból kiinduló ágak száma az első fa esetében ugyan kisebb, de ‐ mint ezt a táblázat mutatja ‐ ez nem befolyásolja olyan mértékben az ágak számát, mint a felső csomópontokból kiinduló ágak száma.
A gép természetesen nem mindig járja végig az egész fát; ha megfelelő felosztást talál, megáll. (Ezért például n=8-ra a program gyorsabb, mint n=7-re; holott n=8-ra az ágak száma jóval nagyobb.) Minket ezek az esetek érdekelnek jobban, és nem közömbös számunkra, hogy a gép mennyi idő alatt talál egy megoldást. A második programnak például n=8-ra 12748 ágat kell megvizsgálnia, mire megoldást talál. Az algoritmus újabb módosításával talán tovább lehetne növelni a program sebességét. Indítsuk tehát el a programot, majd állítsuk le és nyomtassuk ki a V tömb tartalmát. Észrevehetjük, hogy az elhasznált számok között most nagyobbak is vannak, de a kis számok most is túlságosan hamar kerültek sorra; hasonló problémával állunk szemben, mint az első program esetében. Amikor egy csomópont ágait sorbarendezzük, a kisebb első elemű számhármasokat részesítjük előnyben. Ha ez pont fordítva történne, a kis számok jóval később kerülnének felhasználásra.
A változtatás most még egyszerűbb, mint az előbb :
 

3. program
 

  10  DEFINT A‐Z  330  IF K = N THEN 600  20  INPUT "N="; N  340  L =L‐1:IF V(L) =1 THEN 340  30  N3 = 3  *N  350  GO TO 100  40  DIM A(N), B(N), C(N), V(N3)  50  K=0:L=N3  400  IF K=0 THEN 500410  L=C(K):M=A(K)  100  M=(L+1)/2  420  V(M)=0:V(L‐M)=0:V(L)=0  430K=K‐1440  GO TO 200  200  M = M‐1    210  1F M=0 THEN 400  500  PRINT "NINCS MEGOLDÁS"  220  1F V(M) =1 OR V(L‐M) =1  510  END  THEN 200600  FOR 1=1 TO N  300  K = K +1  610  PRINT A(I); B(I); C(I)  310  A(K) = M : B(K) = L‐M C(K) = L  620  NEXT I  320  V(M) =1: V(L‐M) =1: V(L) =1  630  END
 

Most a gép ,,visszafelé'' járja végig a fát. Olyan n értékek esetén tehát, amelyekre nem létezik megfelelő felosztás, a futási idő körülbelül azonos a 2. programéval.
A programot egy olyan n értékkel futtatva, amely 4-gyel osztva 0 vagy 1 maradékot ad, a futási idő rendkívül rövidnek bizonyul:
 

n    8    9    12    13    16    17    20    21    24    25    28    29    32    33    5    16    5    8    25    8    6    6    91    10    15    21    45    100  
 

A program ‐ nagyobb n-ekre ‐ jóval hamarabb talál megoldást, mint az első program gépi kódú változata. (Általában sok megfelelő felosztás van, a három program legtöbbször három különbözőt állít elő.)
A sebességnövekedést azzal magyarázhatjuk, hogy a megoldásokat ,,jó'' helyen kerestük: az új programnak sokkal kevesebb ágat kellett végigjárnia, mint az előzőeknek:
 

n    1    4    5    8    9    12    13    16    17  1. program    1    41    197    7073    54 412    31 963 121    2. program    1     7     13     185       534        12 748    27 920    1 163 696    5 796 896  3. program    1     5      5      19        55            16        24           63           25  
 

A vizsgált élek száma
 

A program gépi kódú változatával sikerült a korábban kimondott sejtést n≦64-re bebizonyítani, a teljes bizonyításhoz azonban nem jutottunk sokkal közelebb. A talált felosztásokban nincs olyan szabályszerűség, ami alapján egy általános konstrukciót lehetne alkotni. Viszont meglevő felosztások felhasználásával új, több elemből álló felosztásokat lehet konstruálni a következő tételek alapján. A továbbiakban ‐ a rövid jelölés kedvéért ‐ jelölje M azoknak az n-eknek a halmazát, amelyekre létezik jó felosztás.
 

1. tétel. Ha k∈M, akkor 3k+1∈M.
 

Bizonyítás
 

Legyen {ai,bi,ci} i≦k-ra egy megfelelő felosztás, vagyis a1, b1, c1, ..., ak, bk, ck az 1, 2, ..., 3k számok egy permutációja és ai+bi=ci minden 1≦i≦k-ra.
Most mutatunk egy jó felosztást n=3k+1-re. A hármas csoportok i=1,2,...,k-ra {3ai,3bi+1,3ci+1}, {3ai-1,3bi,3ci-1}, {3ai+1,3bi-1,3ci};
valamint {1,9k+2,9k+3}.
Ez a felosztás nyilván megfelelő.
 

2. tétel. Ha k∈M és l∈M, akkor 6kl+k+l∈M.
 


Bizonyítás
 

Legyen egy-egy k, illetve l szerinti felosztás {ai,bi,ci} 1≦i≦k-ra, illetve {Aj,Bj,Cj} 1≦j≦l-re. Egy megfelelő felosztás n=6kl+k+l-re a következő:
{(6l+1)ai-3l,(6l+1)bi,(6l+1)ci-3l},{(6l+1)ai-3l+1,((6l+1)bi+1,(6l+1)ci-3l+2},⋮⋮⋮{(6l+1)ai,(6l+1)bi+3l,(6l+1)ci+3l}{(6l+1)ai+1,(6l+1)bi-3l,(6l+1)ci-3l+1},{(6l+1)ai+2,(6l+1)bi-3l+1,(6l+1)ci-3l+3,}⋮⋮⋮{(6l+1)ai+3l,(6l+1)bi-1,(6l+1)ci+3l-1}
 1≦i≦k-ra, továbbá {Aj,Bj,Bj} 1≦j≦l-re.
 
A felosztás első részében az 1,2,...,3k számokat szoroztuk meg (6l+1)-gyel és adtuk hozzájuk egy (6l+1) szerinti maradékosztály, a {-3l,-3l+1,...,+3l} halmaz elemeit. Közöttük tehát bármely kettő különböző, mert vagy (6l+1)-gyel osztva adnak különböző maradékot, vagy kiszámításuk során az n=k szerinti felosztás két különböző elemét szoroztuk meg (6l+1)-gyel, majd ugyanazt a számot adtuk hozzájuk.
A (6l+1)k darab csoport tehát különböző elemeket tartalmaz. A legkisebb és a legnagyobb elem (6l+1)⋅1-3l=3l+1, illetve (6l+1)3k+3l=18kl+3k+3l, ezek között éppen 3⋅(6l+1)k=18kl+3k szám van, a csoportok elemei tehát csak a 3l+1, 3l+2, ..., 18kl+3k számok lehetnek. Ha pedig ezekhez hozzávesszük az {Aj,Bj,Cj}, n=l szerinti felosztást, akkor egy teljes n=6kl+k+l szerinti felosztást kapunk.
 


3. tétel. Ha k∈M, akkor 4k∈M.
 


Bizonyítás
 
Teljesen hasonló az előzőekhez.
Legyen {ai,bi,ci} a k-hoz tartozó felosztás. Ekkor {2ai,2bi,2ci} 1≦i≦k, továbbá {6k+j,6k+1-2j,12k+1-j } 1≦j≦3k-ra megfelelő felosztás n=4k-ra.
 


4. tétel. Ha k∈M, akkor 4k+1∈M.
 


Bizonyítás
 

A konstrukció az előzőnek egy változata: ha {ai,bi,ci } a felosztás, akkor {2ai,2bi,2ci } és {6k+1+j,6k+3-j,12k+4-j } n=4k+1-re felosztás.
Az utóbbi két módszer segítségével 64<n<72-re is tudunk megfelelő felosztásokat gyártani, ám n=72-re nem sikerült a felosztás létezését bizonyítanom.
A számítógépet most egy feladat speciális eseteinek megoldására használtuk, s ez nem vezetett a probléma általános megoldásához. Létezik viszont olyan tétel, amelynek a bizonyításához számítógépre volt szükség.
Mindenki hallott már a híres négyszín-tételről. 5 színre viszonylag egyszerű teljes indukciós bizonyítást lehet adni, amelynek az a lényege, hogy a térkép színezhetőségét egy kevesebb országból álló térkép színezhetőségére vezeti vissza. Ehhez olyan térképrészleteket kell vizsgálni, amelyek valamelyike minden (megfelelő számú országot tartalmazó) térképen előfordul, és ezeket kevesebb országból álló részletekkel helyettesíti. 4 színre a bizonyítás hasonló, csak a megvizsgálandó térképrészletek száma olyan nagy, hogy számítógép nélkül a bizonyításhoz felhasznált idő több év lenne.
Az ilyen bizonyítások ma még elég ritkák, és nem valószínű, hogy valaha is ezek kerüljenek többségbe.