| Cím: | Taktikai utasítások rablóknak és detektíveknek | ||
| Szerző(k): | Károlyi Gyula | ||
| Füzet: | 1987/január, 1 - 9. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Olvasóink közül bizonyára sokan ismerik a "Police 07'' fedőnevű társasjátékot, bevezetőül mégis ejtenék néhány szót ennek lényegéről. A játék egy város térképén zajlik, amelyen számokkal megjelölve közlekedési csomópontok találhatók. A résztvevők ezen csomópontok között ‐ bizonyos szabályok betartásával ‐ különböző járműveken (metró, autóbusz, taxi) közlekedhetnek. A játékosok egyike a menekülő rabló szerepét játssza, a többiek az őt üldöző detektívek. A játék kezdetén a résztvevők sorshúzásos alapon elhelyezkednek a város különböző pontjain, majd megkezdődik a hajsza : a játékosok felváltva lépnek. Egy lépés abból áll, hogy valamelyik közlekedési eszközzel egy megállót mennek. A rablónak azonban komoly előnye van : csak minden ötödik lépés után kell megmutatkoznia a táblán, a közben megtett lépéseit csak jegyeznie kell. A detektívek akkor nyernek, ha korlátozott számú (mondjuk 24) lépésen belül elérik a rablót, ellenkező esetben a rabló a győztes. Van még egy-két kisebb szabály, ezek részletezésére azonban most nem térünk ki. 2. Gráfok Ahhoz, hogy a játékot matematikai eszközökkel tudjuk vizsgálni, célszerű lesz megismerkednünk a gráfok fogalmával. Gráfnak hívunk egy olyan ábrát, amely pontokból és őket összekötő vonaldarabokból áll. A pontokat a gráf csúcsainak, a vonalakat pedig a gráf éleinek nevezzük. Az összekötő szakaszok felrajzolásakor létrejövő esetleges újabb metszéspontokat nem tekintjük a gráf csúcsainak ‐ mint ahogyan egymást keresztező útvonalon közlekedő járművek esetében sem szállhatunk át egyikről a másikra két megálló között. A gráf minden éle tehát két különböző csúcsot köt össze. Egy gráf adott pontjából kiinduló élek számát az illető pont fokának (fokszámának) nevezzük. Feladat. Bizonyítsuk be, hogy egy gráfban a pontok fokszámainak összege szükségképpen páros szám! Egy gráfot regulárisnak hívunk akkor, ha minden pontjának ugyanannyi a fokszáma. Ilyen gráfokat láthatunk az 1. ábrán : mindkét gráfnak csak negyedfokú csúcsai vannak. 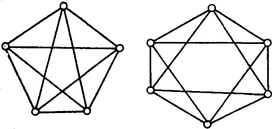 Feladat. Bizonyítsuk be, hogy egy pontú gráfnak legfeljebb éle lehet! Teljes gráfnak hívjuk az olyan gráfokat, amelyekben bármely két csúcsot él köt össze. Az 1. ábrán látható tehát a teljes ötpontú gráf, más néven teljes ötszög. A teljes gráfok nyilván reguláris gráfok. 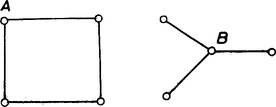 Egy gráf összefüggő, ha bármely két pontja összeköthető úttal: élek egymáshoz csatlakozó sorozatával. A 2. ábra egy nem összefüggő gráfot ábrázol: az és a pontok között nem vezet út. A továbbiakban csak összefüggő gráfokról lesz szó. Előfordulhat, hogy gráfunk egy pontjából kiindulva egymáshoz illeszkedő élek mentén haladva visszajutunk a kiindulási pontba. Ekkor a gráfnak egy körét kaptuk. A kör hosszát a benne szereplő élek (csúcsok) száma adja. A 3. ábrán egy olyan gráf látható, amely egyetlen, hosszúságú körből áll. A 4. ábrán levő gráfokban viszont egyáltalán nincs kör, ha egy ilyen körmentes gráf összefüggő is, akkor fának nevezik. 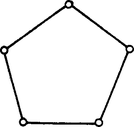 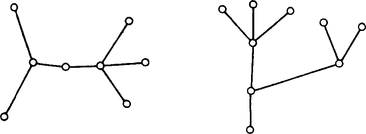 Feladat. Bizonyítsuk be, hogy egy pontú fának éle van! Gráfelméleti tétel húzódik meg a következő állítás mélyén: egy társaságban mindig található két ember, akiknek a társaságban ugyanannyi ismerősük van. Ha a társaság tagjait egy gráf csúcsainak, a köztük fennálló (kölcsönös) ismeretségeket pedig a gráf éleinek tekintjük, akkor állításunk így hangzik : tetszőleges gráfnak van két azonos fokszámú csúcsa. Feladat. Igazoljuk a fenti állítást. Mármost az első részben említett játék is kapcsolatba hozható a gráfokkal: a közlekedési csomópontokat tekinthetjük egy gráf csúcsainak, ahol két csúcsot akkor kötünk össze éllel, ha a nekik megfelelő két csomópont közvetlenül (egy lépésben) elérhető egymásból valamelyik közlekedési eszközzel. 3. Mit tehet detektív? Először a játéknak egy igen leegyszerűsített változatát vizsgáljuk meg. Mindössze egy detektív üldözi a rablót, aki tehát most nem rejtőzhet el, üldözője mindig ismeri a pillanatnyi tartózkodási helyét. Először a detektív üti fel hadiszállását a város egy alkalmas pontján, majd a rabló a menekülésre leginkább előnyös helyet választja ki. Ha az üldözés során a rabló úgy érzi, jó helyen van, egy ideig ott is maradhat, a detektívnek azonban mindig haladnia kell. Mit jelent ez a gráfok nyelvén? A színtér egy (összefüggő) gráf, amelynek előbb a detektív, majd a rabló kiválasztja valamelyik csúcsát, majd felváltva lépnek a gráf élei mentén. A rabló azonban megteheti azt is, hogy valamelyik lépése helyett helyben marad. A detektív akkor nyer, ha elfogja a rablót, vagyis ha rálép a gráfnak arra a csúcsára, ahol a rabló tartózkodik. Mármost ekkor az összefüggő gráfok két osztályba sorolhatók : -be tartoznak azok a gráfok, ahol a detektívnek van nyerő stratégiája (bárhonnan is induljon a rabló), -be pedig a többi gráf, ahol tehát a rabló megmenekülhet, ha ügyesen játszik. Természetesen, ha a rabló elrontja a manőverezést, akkor a detektív is nyerhet -beli gráfokon. Lássunk először egy-két példát. (a) osztályba tartoznak például a fák. A detektív által elfoglalt csúcs ugyanis két részre osztja a gráfot. Ha a detektív mindig a rabló felé mozog (ez egyértelmű, minthogy a gráfban nincs kör), akkor az a rész, amelyben a rabló tartózkodik, a detektív minden egyes lépésével csökken. Így az előbb-utóbb egy pontra zsugorodik, ekkor pedig a rabló fogva van. (b) osztályba tartoznak azok a gráfok, amelyek egyetlen, legalább hosszúságú körből állnak. A rabló ugyanis elhelyezkedhet úgy, hogy távolsága a detektívtől legalább lépés legyen, és ezt a távolságot tartani is tudja. (c) Minthogy a körök 2-reguláris gráfok, az előző állítás általánosításaként bizonyítható, hogy -be tartozik az összes olyan reguláris gráf, amelyik nem teljes (a teljes gráfok nyilván -beliek). (d) Az 5. ábrán látható gráf szintén -beli (de ha a rablónak is mindig lépnie kellene, akkor -beli lenne).  A következőkben megpróbáljuk jellemezni a -beli gráfokat, és ily módon eljárást is nyerünk annak eldöntésére, hogy egy gráf melyik osztályba tartozik. Vizsgáljuk először azt, hogy egy -beli gráfban hogyan érhet véget a játék. A rabló utolsó lépése előtt a detektív és a rabló két szomszédos (éllel összekötött) csúcsban tartózkodik, hiszen egyébként a rabló helyben maradhatna. Ezután a rabló vagy egyenesen az üldözője karjaiba szalad, vagy valamelyik, a detektívével szomszédos csúcsra lép (esetleg helyben marad), és ott a detektív elfogja. Nevezzük ezt a helyzetet csapdának: olyan pontot a gráfban, amelynek van olyan szomszédja, hogy és a -nek minden -tól különböző szomszédja egyben -nak is szomszédja. A fentiek szerint, ha a rabló jól játszik, akkor a detektív csak úgy nyerhet, ha ellenfelét egy ilyen csapdába tereli, ő maga pedig a vele szomszédos csúcsra lép. A 6. ábrán látható gráf (ami az oktaéder élhálózata) tehát az osztályba tartozik, hiszen nincsen benne csapda. 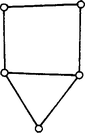 Ezzel ugyan még nem értünk célhoz, hiszen elképzelhető, hogy egy gráf tartalmaz ugyan egy vagy több csapdát, a rabló azonban tud úgy lépegetni, hogy ezeket mindig elkerülje. Ezért lesz hasznos a következő észrevétel. Tegyük fel, hogy egy gráf tartalmaz egy csapdát. Ekkor elkészíthetünk egy gráfot a következő módon : a gráfnak elhagyjuk a csúcsát, élei közül pedig azokat, amelyek -hez illeszkednek. Ezt a műveletet szemlélteti a 7. ábra.  Feladat. Bizonyítsuk be, hogy a gráf is összefüggő. Ezen művelet birtokában megfogalmazhatjuk a következő tételt : 1. Tétel: Tegyük fel, hogy a (összefüggő) gráfban található egy csapda. Ekkor pontosan akkor -beli, ha a fenti módon elkészített gráf is az. Bizonyítás. Tegyük fel először, hogy a -beli, és tekintsük a csapdával szomszédos pontot. A detektív egyszerű módon terjesztheti ki a -beli nyerő stratégiáját a -re (bizonyítva ezzel, hogy -beli), a következő módon. Ha a rabló -ben a -től különböző pontra lép, akkor a stratégia egy az egyben alkalmazható, ha pedig -be lép, akkor és már elemzett kapcsolata miatt a detektív úgy járhat el -beli stratégiája szerint, mintha a rabló -ban volna. Minthogy a játék a -ben előbb-utóbb a detektív győzelmével ér véget, -ben két eset lehetséges : ha a -beli játék a -tól különböző pontban végződött, akkor ugyanitt a -beli játék is véget ér; ha pedig a -beli játék a -ban fejeződik be, akkor előfordulhat az is, hogy -ben a rabló ilyenkor a helyett a -ben lapul: ekkor azonban a detektív a következő lépésében fülön csípi, hiszen -ben a csapda. Ha pedig azt tesszük fel, hogy -beli, akkor a rabló tudja stratégiáját hasonló módon átvinni -re, és ez bizonyítja, hogy ekkor is -beli. Ez a tétel már valóban elegendő ahhoz, hogy jellemezzük a -beli gráfokat. Eszerint a gráf pontosan akkor -beli, ha egymás után eltávolítva belőle a csapdákat (tetszés szerinti sorrendben) végül is egy egypontú gráfhoz jutunk. Ennek alapján könnyen látható, hogy például a 8. ábrán feltüntetett gráf a osztályba tartozik. Az ábrán -vel megjelöltük a csapdákat, az egyes lépések valójában lépést foglalnak össze. 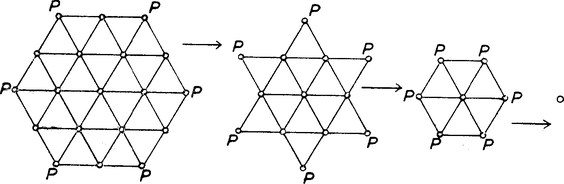 Ez a tétel tehát viszonylag gyors eljárást szolgáltat annak eldöntésére, hogy egy gráf melyik osztályba tartozik, és ha jól végiggondoljuk, akkor a rabló vagy a detektív nyerő stratégiájának megkeresésére is. 4. Rablók előnyben Most kibővítjük az előző játékot azzal a lehetőséggel, hogy a rendőrség egynél több emberrel üldözheti a rablót. Ekkor a lépésszabály így módosul: a rendőrség egy lépése abból áll, hogy tetszés szerinti emberei lépnek egyet-egyet (tehát nem kell az összes detektívnek elmozdulnia), de legalább egy detektívnek lépnie kell. Azt vizsgáljuk tehát, hogy ilyen feltételek mellett milyen gráfok kedveznek a rablónak és melyek a rendőrségnek. Elég sok detektív persze mindenütt elfogja a rablót, épp akkor tekintsünk egy gráfot a rabló számára kedvezőnek, ha elfogásához viszonylag sok detektívre van szükség. Érdemes tehát minden gráfhoz egy számot rendelni, amely azt mutatja meg, hogy legalább hány detektív kell ahhoz, hogy bárhogyan is menekül a rabló, elcsípjék őt. Az előző rész osztályához tartozó gráfokra tehát , az -beliekre pedig Ebben a részben tehát azokat a gráfokat próbáljuk elemezni, amelyekre nagy. 2. Tétel: Tegyük fel, hogy a gráf minden pontjának foka legalább és nem tartalmaz sem sem pedig hosszúságú kört. Ekkor Bizonyítás. Tegyük fel először, hogy a detektívek száma kisebb mint , és valahogy elhelyezkedtek a gráf csúcsain. Ha most a rabló az csúcsban van, akkor tekintsük az -val szomszédos csúcsokat. Ezek száma a fokszámra kirótt feltétel miatt legalább Rablónk nem léphet egy ilyen, -val szomszédos csúcsra, ha ott vagy egy azzal szomszédos csúcson detektív áll ‐ ekkor azt mondjuk, hogy az csúcs szóban forgó szomszédját őrzi egy detektív. Ha -t vagy annak valamelyik szomszédját egyetlen detektív sem őrzi, akkor a rabló minden további nélkül helyben maradhat, illetve az őrizetlen csúcsba léphet, a következő lépésben így biztosan nem kaphatják el. Ha most észrevesszük azt, hogy egy detektív nem őrizheti -nak két különböző szomszédját egyszerre (hiszen akkor épp egy vagy hosszúságú kört kapnánk -ben), akkor látszik, hogy van -nak olyan szomszédja, amelyre a rabló ráléphet, nem kockáztatva azt, hogy a következő lépésben elfogják. Ha tehát a rabló egyszer elhelyezkedett a táblán úgy, hogy a következő lépésben ne foghassák el, akkor vég nélkül lépegethet a leírt módon. Hol bújjon meg kezdetben? Az eddigiek ismeretében erre könnyű a válasz: szemeljen ki egy csúcsot, ahol nem áll detektív, és helyezkedjen el ennek a csúcsnak egy olyan szomszédján, amelyet egyetlen detektív sem őriz. Mivel a fentiek szerint ilyen csúcs létezik, a rablónak valóban van nyerő stratégiája, tehát valóban  A tétel következményeként adódik, hogy a 9. ábrán látható Petersen-gráf, illetve a dodekaéder élhálózatán legalább 3 detektív szükséges az eredményes nyomozáshoz. Felmerül azonban a kérdés, vajon léteznek-e minden -re a felsorolt feltételeket kielégítő gráfok. Erre ad igenlő választ a következő 3. Tétel: Minden természetes számra létezik olyan -reguláris gráf (tehát ahol minden pont foka ), amely nem tartalmaz sem 3, sem pedig 4 hosszúságú kört. Ezért minden -re létezik olyan gráf, amelyre Ezt a tételt nem bizonyítjuk. Vannak azonban feltételek, amelyek a rendőrség dolgát könnyítik meg. Válasszuk ki a gráf néhány csúcsát. Ezekről azt mondjuk, hogy lefogó pontrendszert alkotnak, ha a gráf minden egyes éle valamelyik kiválasztott ponthoz illeszkedik. Vagy ami ezzel egyenértékű: a gráf minden további pontja szomszédos valamelyik kiválasztott ponttal. Ha most a detektívek a játék elején egy ilyen lefogó pontrendszert foglalnak el, akkor a következő lépésben elérik a rablót. Ezért egy gráfra nem lehet nagyobb egy lefogó pontrendszer elemszámánál sem. Teljes gráfban például egyetlen pont is lefogó pontrendszer, az itt lesben álló detektív a következő lépésben megfogja a rablót, bárhol is áll. Ez a becslés elég durva: a játékot még szinte el sem kezdtük és már véget is ért. Sok esetben azonban radikálisan javítható. Erről szól a következő két tétel. 4. Tétel: Ha egy gráf minden pontjának a foka legfeljebb 3, valamint a gráf bármely két szomszédos élét magában foglalja a gráf egy legfeljebb hosszúságú köre, akkor . Ebből következik, hogy a 9. ábrán látható gráfokra . Bizonyítás. Megmutatunk egy nyerő stratégiát detektív számára. Tegyük fel, hogy a rendőrség egy lépése után a detektívek a a rabló pedig az csúcsban van. Vezessünk egy-egy utat a pontokból az -be úgy, hogy ezek az -ből kiinduló minden élt (ilyen legfeljebb van) érintsenek. A második feltétel miatt ez megtehető. Jelölje a út hosszát, vagyis a benne szereplő élek számát. A , , utakat válasszuk meg úgy, hogy összhosszuk: minimális legyen. Belátjuk, hogy bármit is lép a rabló, a detektívek alkalmas pontokba léphetnek úgy, hogy legyen. Ez azt jelenti, hogy véges sok lépés után az értéke alá csökken, ami éppen azt jelenti, hogy valamelyik detektív elfogta a rablót. Tegyük fel, hogy -nek pontosan három szomszédja van (a többi eset hasonlóan, de egyszerűbben kezelhető), a út az pont szomszédján vezet keresztül (10. ábra).  Ha a rabló helyben marad, mindegyik detektív léphet egyet a úton felé, és így Tegyük fel, hogy a rabló ellép, mondjuk az pontba. Ha , akkor a játék ezzel véget is ér, ha , akkor két eset lehetséges: -nek vagy , vagy szomszédja van. Az első esetben, ha mindegyik detektív egyet lép felé, adódik. A második esetben legyen az -nek az a szomszédja, amelyik nincs rajta -en. Az és az élek a feltétel szerint a gráf egy legfeljebb hosszúságú körében vannak, ez a kör pedig tartalmazza még valamelyik -ből induló élt, mondjuk az -t. A kör esetleges ötödik pontja legyen . Ekkor a 11. ábrának megfelelően mozogva, , , választással adódik, tehát valóban minden esetben amint azt állítottuk. Ezzel pedig a tételt igazoltuk. 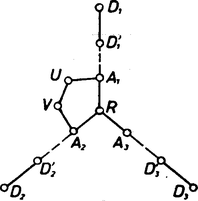 * A továbbiakban szükségünk lesz a síkgráf (vagy síkba rajzolható gráf) fogalmára. Egy gráfot akkor mondunk síkba rajzolhatónak, ha pontjai és a köztük haladó élek felrajzolhatók a síkra úgy, hogy a különböző élek ne keresztezzék egymást. A 12. ábrán látható gráf például a látszat ellenére síkba rajzolható (13. ábra). Nem ilyen azonban a 14. ábrán látható két gráf: a teljes ötszög és a "három ház ‐ három kút'' nevet viselő gráf. Az olvasó megpróbálkozhat ezen gráfok síkba rajzolásával, ez azonban nem fog sikerülni. 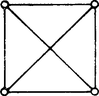 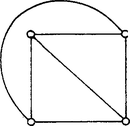  Ennek a két gráfnak alapvető szerepe van a síkgráfok elméletében, ugyanis Kuratowski lengyel matematikus tétele értelmében egy gráf pontosan akkor síkba rajzolható, ha nem tartalmaz olyan részgráfot, amely az előző kettő valamelyikére húzható össze (összehúzáson a következő eljárás ismételgetését értjük: a gráf egy másodfokú pontját elhagyjuk, és a belőle kiinduló két él addig még össze nem kötött végpontját összekötjük). A következő szép tétel a síkgráfok egy különleges tulajdonságát mutatja : 5. Tétel: Minden síkgráfra . 6. Ismét Police 07 A bevezetőben ismertetett társasjátékra több modellt is megvizsgáltunk. Tekinthetnénk olyan játékokat is, ahol a detektíveknek csak részleges információi vannak a rabló helyzetéről, például csak minden ötödik lépés után tudják pontosan a rabló helyét, vagy csak akkor szereznek erről tudomást, ha legfeljebb két lépés távolságra megközelítették őt. Részben az 5. tételt is alkalmazhatjuk a társasjátékokra, hiszen, ha pl. csak az autóbuszhálózatot tekintjük, síkba rajzolható gráfot kapunk. A három különböző közlekedési eszköz úthálózata azonban együttesen már nem síkba rajzolható. A játék szépségét és érdekességét éppen az adja, hogy igen nehéz lenne pontos és egyben jól kezelhető matematikai modellt adni rá. Befejezésül megemlítem, hogy az eddigi tapasztalat azt mutatja, hogy négy rátermett detektív majdnem mindig elfogja a rablót. Igazán izgalmasnak tehát három detektív esetén ígérkezik a játék. Jó szórakozást! |