Cím: A rendezetlen kapcsolatok fizikája - A perkolációs modell
Szerző(k):  Kertész János 
Füzet: 1986/december, 465 - 469. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Képzeljünk el egy gyümölcsöskertet, amelyben a fák szabályos négyzetrácsban helyezkednek el. Ha egy betegség valamelyik fánál felüti a fejét, akkor az átterjedhet a szomszédos fákra. Az átterjedés véletlenszerű és p valószínűséggel következik be. Ez a p függ a fák egymástól mért távolságától: minél közelebb vannak egymáshoz a fák, annál valószínűbb, hogy a fertőzés átterjed. Hogyan lehet a fákat elég közel ültetni egymáshoz, hogy sok gyümölcsfánk legyen és ugyanakkor elkerülni, hogy az egész kertre kiterjedő járványok keletkezzenek?

 

2. A hagyományos eszpresszó-kávéfőző vázlatát mutatja az 1. ábra. Melegítés hatására a víz fölött a gőznyomás megnő és átnyomja a vizet a tölcséren, amelyben a kávéőrleményt elhelyezték. A kávészemcsék közötti úton áthaladva a forró víz kioldja a kávé hatóanyagait. Minél sűrűbben pakolják a kávét, annál zegzugosabb, hosszabb lesz a víz útja ‐ annál erősebb lesz az ital. Túl nagy sűrűség esetén azonban előfordulhat, hogy a víz az adott nyomáson nem talál kivezető utat ‐ a kávéfőző felrobbanhat. (A kávéfőző angolul percolator; percolation = szivárgás.)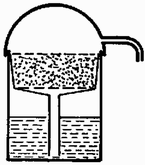
 
 
1. ábra
 

3. Glicerol és valamilyen kétértékű szerves sav észteresedésénél térháló jön létre. Az egyszerűség kedvéért jelöljük a glicerolt egy ponttól kiinduló három pálcikával, annak megfelelően, hogy három alkoholos "lába'' van (a 2. ábra bal oldalán látunk ilyet), a kétértékű savat pedig egy pontból kiinduló két pálcikával (ilyen a 2. ábra jobb oldalán látható). (Az x-szel jelölt helyekről vízkilépés történik.) A kialakuló térháló elérheti az edény méreteit és mechanikai szilárdságot adhat a rendszernek. Ez a gél fázis. Hasonló átmenet figyelhető meg pl. kocsonya készítésekor, vagy a gumi vulkanizálásánál.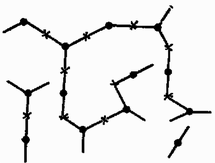
 
 
2. ábra
 

4. Tekintsünk egy kristályrácsot, amelyben mágneses atomok vannak p koncentrációval, vagyis az atomok p-ed része mágneses. Tegyük fel továbbá, hogy a mágneses kölcsönhatás rövid hatótávolságú, csak közvetlen szomszédokra terjed ki. Alacsony p érték esetén a mágneses atomok kis szigetekben helyezkednek el, amelyek nem érzik egymás hatását. Növelve p -t egyre nagyobb fürtöket találhatunk, amelyekben (elegendően alacsony hőmérsékleten) az "elemi mágnesek'' párhuzamosan állnak, de mivel az egyes fürtök függetlenek egymástól, kioltják egymás hatását, és kifelé a rendszer továbbra sem mágneses. Ahhoz, hogy 0-tól különböző mágnesezettséget kapjunk, p-t addig kell növelni, amíg meg nem jelenik egy, az egész rendszerre kiterjedő fürt, mágneses atomokból (3. ábra).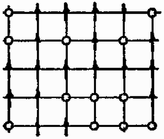
 
 
3. ábra
 

5. Készítsünk keveréket vezető és szigetelő elemekből (pl. acélgolyók + homok). Mérjük a rendszer vezetőképességét! A vezetőképesség gyakorlatilag 0 lesz, amíg nem jön létre egy út a töltéshordozók számára, amely az egész rendszerre kiterjed. Lesz tehát egy olyan kritikus koncentrációja az acélgolyóknak, aminél a vezetőképesség elkezd növekedni.
A fenti példák közös vonása, hogy bennük rendezetlenség hatására létrejövő véletlen kapcsolatok döntő szerepet játszanak. Mivel hasonló jelenségekkel nagyon sok területen lehet találkozni, érdemes elvonatkoztatni a konkrét tulajdonságoktól és a közös jellemzőket tartalmazó modellt vizsgálni. Ez a perkolációs modell.
Képzeljünk el egy végtelen rácsot, amelyben a kötések p valószínűséggel betöltöttek (feketék), és 1-p valószínűséggel nem betöltöttek (fehérek). A 4. ábra a négyzetrács példáját mutatja. Az egymásból betöltött (fekete) éleken keresztül elérhető rácspontok együttese fürtöt alkot.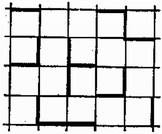
 
 
4. ábra
 

A betöltöttség jelenthet fertőzésátvitelt (1), a kávészemcsék között a folyadék számára járható utat (2), kialakult kémiai kötést (3) stb. Az itt ismertetett modell a kötésperkoláció. Ha nem a rács kötéseit, hanem pontjait töltjük be p valószínűséggel (pl. 3. ábra), akkor rácspont-perkolációs problémával állunk szemben. Növeljük a p-t 0-tól 1-ig. Kezdetben csak kis elszigetelt fürtöket látunk. Lesz azonban egy kritikus érték, pc, amelynél megjelenik egy, az egész rendszerre kiterjedő végtelen fürt.
 
 
5. ábra
 

Legyen P∞ annak a valószínűsége, hogy egy tetszőlegesen kiválasztott rácspont a végtelen fürthöz tartozik. Ez a perkolációs valószínűség. Nyilván p<pc-re P∞=0. Az 5. ábrán folytonos vonallal vázoltuk P∞ változását p függvényében. Egészen közel pc-hez P∞ arányos (p-pc)β-nal, ahol β egy kritikus exponens. Az exponens értéke csak a perkolációs rendszer dimenziójától függ, tehát attól nem, hogy háromszög vagy négyzetrácson stb. vizsgáljuk a perkolációt, rácspont- vagy kötés-betöltést nézünk. A kritikus exponensnek ezt a nagyfokú függetlenségét a körülményektől univerzalitásnak nevezzük. (Hasonló jelenségekkel a termodinamikai fázisátalakulásoknál ‐ pl. folyadék ‐ gőz átmenetnél lehet találkozni.) Az univerzalitás alapján várható, hogy valódi fizikai rendszerekben, ahol perkolációs átmenet van, a β értéke megegyezik a modellen definiáltéval: 0,139 két dimenzióban és 0,45 háromban. Egy dimenzióban β nincsen értelmezve, hiszen egy láncot teljesen be kell tölteni ahhoz, hogy végtelen fürt alakuljon ki rajta ‐ ezért pc=1 és nincsen p>p, tartomány. Egy dimenzióban azt is meg lehet mondani, hogy mi adott p-nél az s méretű fürthöz tartozás valószínűsége (tetszőlegesen kiszemelt pontra). Ez a valószínűség pl. rácspont-perkoláció esetén s(1-p)2ps, amint azt az olvasó könnyen igazolhatja.
Sajnos a fizikailag érdekes két- és háromdimenziós esetben már nem ilyen egyszerű a helyzet. Egzaktul ismert még néhány kétdimenziós probléma kritikus pontja ‐ pl. a négyzetrács kötésperkolációnál pc=1/2. (Az 1. példában feltett kérdésre tehát azt lehet válaszolni, hogy a fákat olyan távol kell egymástól ültetni, hogy p<1/2 legyen.) De már a P∞ függvényt ilyenkor sem ismerjük, és általában már pc meghatározásához is közelítő módszerekhez kell folyamodni.
Az egyik legalkalmasabb eljárás a rendszer számítógépes lejátszása, szimulálása. A véletlen betöltéshez ún. véletlenszámok kellenek. Ilyeneket a Monte Carlo-i rulett segítségével állíthatunk elő, (innen a véletlenszámokat használó számítások elnevezése: Monte Carlo módszer). Célszerű azonban a véletlenszámokat számítógépen meghatározni. A véletlenszám-generátorok olyan algoritmusok, amelyek a (0,1) intervallumban egyenletesen eloszlatott véletlen számokat állítanak elő. Mivel egy algoritmus valójában meghatározott módon kiszámít egy értéket, helyesebb ál-vagy pszeudovéletlenszámokról beszélni, amelyek a matematikában megfogalmazott követelmények alapján véletlenszámoknak tekinthetők. Példák véletlenszám-generátorokra BASIC nyelven:
 
x=1-1.99999*ABS(X-0.5)

vagy
 
A=23876519*X : X=A‐INT (A/12975433)*12975433:X=X/M
 
A legtöbb számítógépen beépített véletlenszám-generátor is található, pl. a COMMODORE 64-en RND(1).
A következő BASIC-program a négyzetrács rácspontperkolációs problémát szimulálja (C 64-en):
 
1 INPUT"L";L:INPUT"P";P
2 FOR  J=1TOL:FOR K=1TOL
3 IF  RND(1)>P  THEN  GOTO  5
4 POKE55270+40*J+K,1:POKE998+40*J+K
5 NEXT K : NEXT J
6 END
 
A program első sora az L×L-es minta méretét és a P betöltési valószínűséget olvassa be. A második sorban egy kettős ciklus kezdődik (K a sorokat, J az oszlopokat jelöli a mintán). A 3. sort lehet Monte Carlo döntésnek nevezni: itt dől el, hogy a K, J koordinátájú pont betöltésre kerül-e. Ha a generált véletlenszám (RND(1)) kisebb vagy egyenlő P-vel akkor igen, különben a ciklus végére (5. sor) ugrunk. Betöltés esetén a képernyő megfelelő négyzetét fehérre festi a 4. sor. Mire a program lefut, a képernyőn előttünk áll egy perkolációs minta. Ezen szemmel eldönthető, hogy lehet-e É‐D vagy K‐NY irányban perkolálni. Különböző p értékek beadásával a kritikus pontról lehet információt szerezni. Fontos a rendszer kis méretéből eredő erős ingadozásokat statisztika segítségével kiszűrni, és figyelembe venni, hogy lehetnek a véges mérettel együtt változó ún. szisztematikus eltérések. (Tájékoztatásul: pc≈0,593.)
Térjünk most át valamilyen fizikai tulajdonság perkolációs rendszeren történő kiszámítására. A legkézenfekvőbb feltenni, hogy egy kötésperkolációs rácson a betöltött éleknek R ellenállásuk van, a be nem töltött élek pedig legyenek tökéletes szigetelők, vagy ami ugyanaz: töltsük be a rácsot p valószínűséggel σ=1R vezetőképességű elemekkel és (1-p) valószínűséggel 0 vezetőképességű elemekkel. A kérdés most már az, hogy mekkora lesz egy ilyen módon létrehozott nagy (makroszkópikus) minta vezetőképessége.
Ezt általánosan kiszámítani nem tudjuk ‐ hiszen ennek a feladatnak a geometriai perkolációs probléma részfeladata, és már azzal sem boldogultunk az egzaktság szintjén. Közelítő módszerhez kell folyamodni, ami ebben az esetben az ún. effektív tér elmélet lehet.
A gondolatmenet ‐ amelyet a fizikában egyébként igen széles körben alkalmaznak ‐ a következő: Adva van egy sok elemből álló rendezetlen rendszer, amelynek makroszkopikus tulajdonságára vagyunk kíváncsiak. Feltesszük, hogy rendszerünk helyettesíthető egy olyannal, amelynek elemei már rendezettek. Esetünkben a véletlenszerűen betöltött rácsot egy teljesen betöltött ráccsal fogjuk leírni: Az új rendszer elemeinek jellemzőit ‐ itt az egyedi gm effektív vezetőképességeket ‐ úgy kell megválasztani, hogy azok kiadják a keresett makroszkopikus mennyiséget. Az elemi jellemzők meghatározásához feltesszük, hogy egy kiválasztott elemtől eltekintve az effektív érték érvényesül a rendszerben. A kiválasztott elemen pedig figyelembe vesszük a lehetséges állapotokat, de ‐ mivel az effektív jellemző kiátlagolt mennyiség ‐ ezek hatásának el kell tűnnie.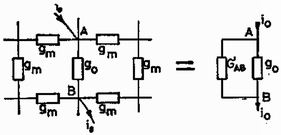
 
 
6. ábra
 

Vizsgáljuk tehát a következő problémát: Adott egy rács, amelynek elemei gm vezetőképességűek, kivéve egy élt, amelyen a vezetőképesség g0 és amelyről feltesszük, hogy p valószínűséggel σ, 1-p valószínűséggel 0 értéket vesz fel (6. ábra). Ha g0 is gm lenne, akkor a feszültség sorról sorra Vm-mel esne, így azonban a gm-g0 különbségből eredő eltérést kompenzálni kell az A pontban bevezetett és B pontból elvezetett i0 árammal, ha a feszültségcsökkenést továbbra is egyenletesnek akarjuk tartani. Természetesen a
Vm(gm-g0)=i0(1)
egyenlet határozza meg i0-t. Tetszőleges gm esetén ilyenkor az A és a B pontok között egy V0 külön feszültségjárulék esik annak következtében, hogy i0 folyik A és B között, tehát
V0=i0(g0+G'AB),
ahol G'AB az egész rács A és B pontok között mérhető vezetőképessége, ha az AB él nincs jelen. Nyilván G'AB=GAB-gm, ahol GAB a gm vezetőképességű élekkel teljesen betöltött rács vezetőképessége AB között. GAB kiszámításához először fontoljuk meg, hogy mekkora feszültség esik AB között, ha i0-t A-nál be-, B-nél pedig kivezetik. Ha külön vezetjük be, ill. ki az áramot, akkor szimmetria okok miatt nyilvánvaló, hogy mindkét esetből i0/4 járulék adódik; tehát az AB élen összesen i0/2 áram folyik, amiből
 
GAB=i0/(i0/2gm)=2gm,vagyisG'AB=gm.

 

V0-ra tehát V0=i0/(g0+gm) adódik. Az effektív tér elmélet alapján ettől a V0-tól követeljük meg, hogy átlagban tűnjön el. Mivel g0p valószínűséggel σ és (1-p) valószínűséggel 0, (1) felhasználásával
(V0)átlag=pVm(gm-σ)/(gm+σ)+(1-p)Vm,
vagyis gm=(2p-1)σ. Látható, hogy a vezetőképesség p=1/2-ben, a négyzetrács kötésperkoláció kritikus pontjában 0-vá válik, tehát az itt vázolt közelítő elmélet az egzakt perkolációs küszöböt ebben az esetben visszaadja. Megjegyezzük, hogy összevetve az elmélet eredményeit pl. szimuláció útján nyertekkel, az egész 1/2≤p≤1 tartomány nagy részén kitűnő az egyezés, csak pc közvetlen környezetében mutatkozik eltérés. Természetesen az effektív tér elmélet nemcsak négyzetrácsra, hanem tetszőleges rácsra alkalmazható az itt vázolt formában.
 
Összefoglalva: perkolációs problémával állunk szemben, ha valamilyen rendszer tulajdonságai a benne levő véletlenszerűen létrejött ‐ vagy megszakadt ‐ kapcsolatoktól függenek. Célszerűnek bizonyult a modell-alkotás: a perkolációs modell matematikai formában fogalmazza meg a vizsgált jelenség lényegét. Egzakt megoldásokat sajnos csak kevés és többnyire érdektelen (pl. 1-dimenziós) esetben ismerünk. Ezért közelítő módszerekhez kellett folyamodni: ilyenek a Monte Carlo szimuláció és az effektív tér elmélet. A perkolációs jelenségkör különösen vonzó sajátossága, hogy a problémák közérthetően megfogalmazhatók, és gyakran az alkalmazott módszerek is viszonylag egyszerűek. Így azután előfordulhat, hogy középiskolás diák is részt vesz új kutatási eredmények létrehozásában.
 
Kertész János

MTA Műszaki Fizikai Kutató Intézete