Kezdőlap


Cím:	Az 1986. évi (17.) Nemzetközi Fizikai Diákolimpia feladatai
Szerző(k):	Gnädig Péter , Honyek Gyula
Füzet:	1986/november, 403 - 414. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A XVII. Nemzetközi Fizikai Diákolimpia feladatai

(Harrow‐1986)

Elméleti feladatok

1. feladat. Egy

λ

hullámhosszúságú és

f

frekvenciájú monokromatikus sík fényhullám esik merőlegesen két azonos méretű keskeny résre. (Ezeket az 1. ábrán

L

és

M

jelöli, egymástól mért távolságuk

d

.) Az egyes réseket elhagyó hullámokat

Θ

irányban mérve (

x

távolságban,

t

időpillanatban) a következő összefüggés adja meg: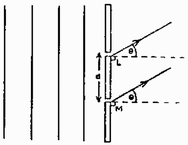

\begin{matrix} y = a cos [2 π \cdot (f t - x / λ)], \end{matrix}

ahol az

a

amplitúdó mindkét hullám esetén ugyanakkora. (Tegyük fel, hogy

x

sokkal nagyobb, mint

d

1. ábra

(i) Mutasd meg, hogy az a két hullám, amelyeket a résekre merőleges irányhoz képest

Θ

szögben észlelünk, olyan

A

eredő amplitúdóval rendelkezik, amit 2 vektor összeadásával kaphatunk meg, mindkettőjük nagysága

a

, és a hozzájuk tartozó irányokat a fényhullám fázisa határozza meg.
Igazoljuk geometriailag a vektorábra alapján, hogy

\begin{matrix} A = 2 \cdot a \cdot cos β, \end{matrix}

ahol

\begin{matrix} β = \frac{π}{λ} \cdot d \cdot sin Θ . \end{matrix}

(ii) Cseréljük ki a kettős rést egy optikai ráccsal, amelyben

N

számú azonos, egyenletesen elhelyezett rés van, és a szomszédos rések

d

távolságra helyezkednek el egymástól. Használd az amplitúdók "vektor-összeadási'' módszerét annak megmutatására, hogy a vektor-amplitúdók (melyek mindegyikének nagysága

a

) egy szabályos sokszög egy részét képezik. A sokszög csúcspontjai egy

R

sugarú körön helyezkednek el, ahol

\begin{matrix} R = \frac{a}{2 \cdot sin β} . \end{matrix}

Vezesd le, hogy az eredő amplitúdó

\begin{matrix} a \frac{sin N β}{sin β}, \end{matrix}

és add meg az eredő fáziskülönbséget a rács széléről kiinduló fény fázisához képest!
(iii) Vázold fel egyazon grafikonon a

sin N β

és az

1 / sin β

értékeit

β

függvényében! Egy másik grafikonon mutasd meg, hogyan változik az eredő hullám intenzitása

β

függvényében!
(iv) Határozd meg a fő intenzitásmaximumok nagyságát!
(v) Mutasd meg, hogy a fő maximumok száma nem haladhatja meg a

\begin{matrix} (2 d / λ + 1) \end{matrix}

értéket!
(vi) Mutasd meg, hogy a

λ

és a

λ + Δ λ

hullámhosszúságú két hullám

(Δ λ ≪ λ)

olyan fő maximumokat ad, amelyeknek szögeltérése:

\begin{matrix} Δ Θ = \frac{n \cdot Δ λ}{d cos Θ}, ahol n = 0, \pm 1, \pm 2, ... \end{matrix}

Számítsd ki ezt a szögeltérést a nátrium

D

vonalaira, amelyekre

\begin{matrix} λ = 589, 0 nm, λ + Δ λ = 589, 6 nm, n = 2 \end{matrix}

és

d = 1, 2 \times 10^{- 6} m

\begin{matrix} [cos A + cos B = 2 cos (\frac{A + B}{2}) cos (\frac{A - B}{2})] . \end{matrix}

Megoldás. (i) Amennyiben az első résből érkező fény fázisa nulla, úgy a másik fázisa

Φ = 2 π / λ \c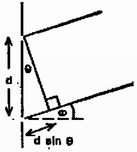dot d \cdot sin Θ

(2. ábra).

2. ábra

Két ‐

Φ

fáziskülönbségű ‐ hullámot összeadva a

ξ = 2 π [f \cdot t - x / λ]

jelölés alkalmazásával

\begin{matrix} a cos (ξ + Φ) + a cos ξ = 2 a cos Φ / 2 cos (ξ + Φ / 2) = 2 a (cos β) cos (ξ + β) \end{matrix}

adódik, ahonnan leolvasható, hogy az eredő hullám amplitúdója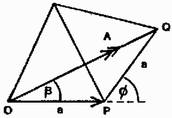

\begin{matrix} A = 2 a cos β, \end{matrix}

fázisa pedig éppen

β

3. ábra

Ugyanez a 3. ábrán látható vektordiagramról is leolvasható. Az

O P Q

egyenlő szárú háromszögben

\begin{matrix} β = \frac{1}{2} Φ = \frac{π}{λ} d sin Θ \end{matrix}

és

\begin{matrix} A = 2 a cos β, \end{matrix}

tehát az eredő hullám olyan két síkbeli vektoramplitúdó összegeként kapható meg, amelyek nagysága

a

, szögeltérésük pedig a hullámok fáziskülönbsége:

Φ

.
(ii) Mindegyik rés egy-egy

a

amplitúdójú, s az előző rés hullámához képest

2 β

fáziseltolású hullámot bocsát ki az adott irányban. A vektordiagram eszerint egy szabályos sokszög részét képezi; az egyes oldalak hossza

a

, az egymás melletti oldalak szöge pedig azonos.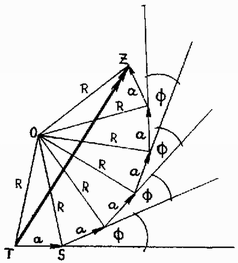

4. ábra

A 4. ábra jelöléseit használva a

T O S

háromszögből leolvashatjuk, hogy

\begin{matrix} R = \frac{a}{2 sin β}, \end{matrix}

T O Z ∢

nagysága pedig

N

-szerese a

T O S ∢

-nek, azaz

N \cdot Φ = 2 \cdot N \cdot β

. Így az eredő hullám amplitúdója

\begin{matrix} \bar{T Z} = 2 \cdot R sin N β = a \frac{sin N β}{sin β} . \end{matrix}

Az eredő hullám fázisa a

Z T S ∢

, amely az

O T S ∢

és

O T Z ∢

különbsége, azaz

\begin{matrix} (90^{\circ} - \frac{Φ}{2}) - \frac{1}{2} (180^{\circ} - N Φ) = \frac{1}{2} (N - 1) Φ = (N - 1) β \end{matrix}

nagyságú.
(iii) A kérdezett függvények az 5. ábrán, az amplitúdó négyzetével arányos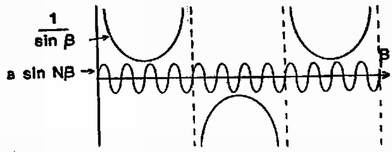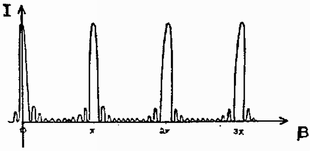

\begin{matrix} I \sim \frac{a^{2} \cdot sin^{2} N β}{sin^{2} β} \end{matrix}

intenzitás pedig az 6. ábrán látható.

5. ábra

6. ábra

(iv) A fő intenzitásmaximumok

β = n \cdot π

értékeknél figyelhetők meg, ahol

n = 0, \pm 1, \pm 2, ...

Ezeknél az intenzitás

\begin{matrix} β = n π + β' és β' \to 0 \end{matrix}

helyettesítéssel

\begin{matrix} I_{max} \sim a^{2} {(\frac{N β'}{β'})}^{2} = N^{2} a^{2} \end{matrix}

nagyságúnak adódik.
(v) A főmaximumoknál

β = n \cdot π

, tehát

\begin{matrix} \frac{π}{λ} d sin Θ = n π (n = 0, \pm 1, \pm 2, ...) . \end{matrix}

Ezt az összefüggést két közeli hullámhosszra,

λ

-ra és

λ + Δ λ

-ra felírva

\begin{matrix} λ = \frac{d sin Θ}{n} \end{matrix}

és

\begin{matrix} λ + Δ λ = \frac{d sin (Θ + Δ Θ)}{n} \end{matrix}

adódik, amelyeket kivonva egymásból, a

Δ λ

hullámhosszkülönbséghez tartozó

Δ Θ

szögkülönbségre a

\begin{matrix} Δ λ = \frac{d}{n} [sin Θ cos Δ Θ + cos Θ sin Δ Θ - sin Θ] \approx \frac{d}{n} Δ Θ cos Θ, \end{matrix}

vagyis a

\begin{matrix} Δ Θ = \frac{n Δ λ}{d cos Θ} \end{matrix}

összefüggés érvényes. Behelyettesítve a

\begin{matrix} Δ λ = 0, 6 \cdot 10^{- 9} m, n = 2 és d = 1, 2 \cdot 10^{- 6} m \end{matrix}

adatokat, továbbá kihasználva, hogy

sin Θ = n \cdot λ / d

Δ Θ = 5, 2 \cdot 10^{- 3} radián = 0, 30^{\circ}

adódik.

2. feladat. Századunk elején a Földről olyan modellt alkottak, amelyben a Földet

R

sugarú gömbnek tekintették, amely a felszíntől lefelé egészen egy

R_{c}

sugárig homogén izotróp (egynemű) szilárd köpenyből áll. Az

R_{c}

sugáron belüli mag tartománya pedig folyadékot tartalmaz. (7. ábra.)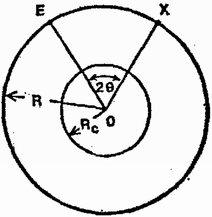

7. ábra

A longitudinális

P

és a transzverzális

S

szeizmikus hullámok sebessége

v_{r}

és

v_{s}

(a köpenyen belül állandó értékűek). A magban a longitudinális hullámok

v_{c P} < v_{P}

sebességűek, míg transzverzális hullámok a magban nem terjedhetnek.
Egy földrengés a földfelszín

E

jelű pontjában szeizmikus hullámokat kelt, amelyek áthaladnak a Földön, és ezeket egy felszínen levő megfigyelő észleli. A megfigyelő a szeizmométerét a Föld felszínének bármely

X

pontjában elhelyezheti. Az

E

és az

X

pontok egymáshoz képesti helyzetét (szögeltérését) a

2 Θ

szög jellemzi:

\begin{matrix} 2 Θ = E O X ∢, \end{matrix}

ahol

O

a Föld középpontja.
(i) Mutasd meg, hogy azok a szeizmikus hullámok, amelyek egyenes vonalban haladnak át a köpenyen, a földrengés után olyan

t

"terjedési idővel'' később érkeznek meg

X

-be, amelyet az alábbi összefüggés ad meg:

\begin{matrix} t = \frac{2 \cdot R \cdot sin Θ}{v}, amennyiben \\ Θ \leq arc cos (\frac{R_{c}}{R}), \end{matrix}

ahol

v = v_{p}

P

hullámokra és

v = v_{S}

S

hullámokra.
(ii) Olyan

X

elhelyezkedés esetén, ahol

Θ > arc cos (R_{c} / R)

, a

P

szeizmikus hullámok a köpeny-mag felületen történő kétszeres törés után érkeznek meg a megfigyelőhöz. Rajzold le egy ilyen

P

típusú szeizmikus hullám útját! Vezess le összefüggést

Θ

és

i

között, ahol

i

P

szeizmikus hullám beesési szöge a köpenymag felületén.
(iii) Felhasználva a következő adatokat

\begin{matrix} R = 6370 km, \\ R_{c} = 3470 km, \\ v_{p} = 10, 85 km/s, \\ v_{S} = 6, 31 km/s, \\ v_{c P} = 9, 02 km/s, \end{matrix}

és a (ii) alkérdésre kapott eredményt, ábrázold a

Θ

szöget az

i

szög függvényében! Állapítsd meg, hogy milyen fizikai következményekkel jár ezen függvényalak a földfelszín különböző pontjain állomásozó megfigyelők számára!
Vázold fel a

P

és az

S

típusú hullámok esetén a terjedési idő változását a

Θ

szög függvényében a

0^{\circ} \leq Θ \leq 90^{\circ}

tartományban!
(iv) Egy földrengés után egy megfigyelő a

P

hullám, majd az azt követő

S

hullám beérkezése között 2 perc 11 másodperc időkülönbséget mér. Határozd meg ebből a (iii) alkérdésben megadott adatok felhasználásával a földrengés helyének és a megfigyelőnek a szögeltérését!
(v) Az előző mérésben a megfigyelő megjegyzi, hogy bizonyos idővel a

P

és

S

hullámok beérkezése után még további két alkalommal jelez a szeizmométer; ezek között az időkülönbség 6 perc 37 másodperc. Magyarázd meg az eredményt és igazold, hogy ez valóban megfelel az előző alkérdésben kiszámított szögeltérésnek!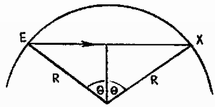

8. ábra

Megoldás. (i) A 8. ábráról leolvasható, hogy az

E

és az

X

pontok távolsága

d = 2 \cdot R \cdot sin Θ

, a terjedés ideje tehát

\begin{matrix} t = \frac{d}{v} = \frac{2 \cdot R \cdot sin Θ}{v}, \end{matrix}

ahol

v

a hullám típusától függően vagy

v_{P}

, vagy pedig

v_{S}

. A fenti összefüggés csak akkor érvényes, ha a hullám végig a köpenyben terjed, tehát a Föld középpontjától mért legkisebb távolsága is legalább

R_{c} :

\begin{matrix} R \cdot cos Θ \geq R_{c}, \end{matrix}

vagyis

\begin{matrix} Θ \leq arc cos \frac{R_{c}}{R} . \end{matrix}

(ii) A köpeny és a mag határfelületén a longitudinális hullám megtörik, éppen úgy, mint a fény egy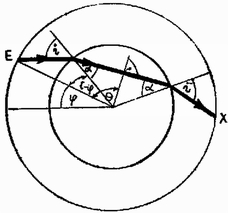

\begin{matrix} n = \frac{v_{p}}{v_{c P}} > 1 \end{matrix}

törésmutatójú anyag határán. Az irányváltozás szöge az optikából ismert Snellius‐Descartes törvényből számolható (9. ábra):

9. ábra

\begin{matrix} \frac{sin i}{sin α} = n, α = arc sin (\frac{sin i}{n}), \end{matrix}

i

beesési szöghöz tartozó

Θ

szög pedig

\begin{matrix} Θ = (90^{\circ} - α) + (i - φ) = \\ = 90^{\circ} + i - arc sin (\frac{R_{c}}{R} sin i) - arc sin (\frac{sin i}{n}) . \end{matrix}

(iii) A megadott számadatok mellett

i

és

Θ

kapcsolatát a 10. ábrán látható függvény adja meg.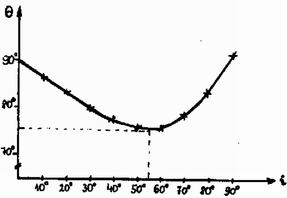

10. ábra

Látható, hogy

Θ > arc cos \frac{R_{c}}{R} \approx 57^{\circ}

és a fenti függvény minimuma

Θ_{c} \approx 75^{\circ}

közötti értékeknek megfelelő

X

helyekre egyáltalán nem jut el szeizmikus hullám.
(iv) A terjedési idő a

Θ > arc cos \frac{R_{c}}{R} \approx 57^{\circ}

-os tartományban kétértékű (az (i) kérdésnek megfelelően), két különböző amplitúdójú szinusz-függvény. Az

57^{\circ}

és

75^{\circ}

közötti tartományban nincs értelmezve a függvény,

Θ > 75^{\circ}

-nál pedig csak a

P

típusú hullámnak megfelelő ág folytatható, ez azonban maga is kétértékű, hiszen a 11. ábráról leolvasható, hogy ezen

Θ

értékekhez kétféle

i

, tehát kétféle ‐ s általában eltérő terjedési idejű ‐ pálya tartozik.

11. ábra

(iv)

P

és

S

hullám csak a

Θ < 57^{\circ}

-os tartományban érkezhet el a megfigyelőhöz. A beérkezés időkülönbsége

\begin{matrix} t = 2 \cdot R \cdot sin Θ \cdot (\frac{1}{v_{S}} - \frac{1}{v_{P}}), \end{matrix}

ahonnan a numerikus adatok felhasználásával

Θ = 8, 92^{\circ}

adódik.
(v) További hullámok a magköpeny határfelületről visszaverődő hullámok lehetnek. Ezek

2 \bar{E P}

távolságot tesznek meg (12. ábra), amelynek nagysága a koszinusz-tétel értelmében

\begin{matrix} s = 2 \sqrt[]{R^{2} + R_{c}^{2} - 2 \cdot R \cdot R_{c} \cdot cos Θ} = 5980 km . \end{matrix}

Ennek a távolságnak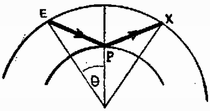

\begin{matrix} t' = (\frac{1}{v_{S}} - \frac{1}{v_{P}}) \end{matrix}

időkülönbség felel meg, s ez valóban 6 perc és 37 másodperccel egyenlő.

12. ábra

3. feladat. Három, egyaránt

m

tömegű részecske egyensúlyban van, miközben olyan (elhanyagolható tömegű) rugók kötik össze őket, amelyek a Hooke-törvényt követik

k

rugóállandóval. A részecskék a 13. ábrán látható módon csak egy kör mentén mozoghatnak.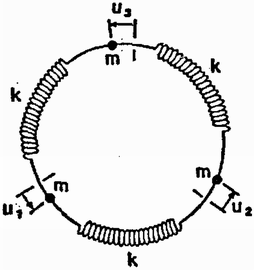

13. ábra

Az egyes részecskéket az egyensúlyi helyzetükből kicsit kimozdítjuk, mégpedig

u_{1}

u_{2}

, illetve

u_{3}

távolsággal.
(i) Írd fel ebben az esetben mindegyik részecske mozgásegyenletét!
(ii) Mutasd meg, hogy az egyenletrendszernek az alábbi egyszerű harmonikus megoldásai vannak:

\begin{matrix} u_{n} = a_{n} cos ω t, (n = 1, 2, 3), \end{matrix}

(- ω^{2} u_{n})

gyorsulásértékekkel, ahol

a_{n} (n = 1, 2, 3)

állandó amplitúdók, az

ω

körfrekvencia pedig az alábbi 2 értéket veheti fel:

\begin{matrix} ω_{0} \sqrt[]{3}, illetve 0, \end{matrix}

ahol

ω_{0}^{2} = k / m

, s az első érték kétszer lép fel.

(iii) A rugók és részecskék egymást váltogató rendszerét terjesszük ki

N

számú részecskére. (Mindegyik

m

tömegű és rugókkal kapcsolódik a szomszédos részecskékhez. Kezdetben a rugók feszítetlenek, és a rendszer nyugalomban van.)
Írd föl az

n

-edik részecske

(n = 1, 2, ..., N)

mozgásegyenletét a szomszédos részecskék elmozdulásainak segítségével, ha a részecskéket kimozdítjuk egyensúlyi helyzetükből!
Igazold, hogy a harmonikus rezgést leíró megoldások

\begin{matrix} u_{n} (t) = a_{s} sin (\frac{2 n s π}{N} + Φ) cos ω_{s} t \end{matrix}

alakúak, ahol

s = 1, 2, ..., N

;

n = 1, 2, ..., N

és

Φ

egy tetszőleges fázis, továbbá

\begin{matrix} ω_{S} = 2 ω_{0} sin (s π / N), \end{matrix}

ahol

a_{s}

(s = 1, 2, ..., N)

n

-től független állandó amplitúdók.
Állapítsd meg a lehetséges frekvenciák tartományát egy olyan lánc esetén, amely végtelen számú tömeget tartalmaz!
(iv) Határozd meg az

\begin{matrix} \frac{u_{n}}{u_{n + 1}} \end{matrix}

arányt nagy

N

-ekre két esetben:
(a) alacsony frekvenciás megoldásokra,
(b)

ω = ω_{max}

esetén, ahol

ω_{max}

a maximális frekvenciájú megoldás.
Vázolj fel az (a), illetve a (b) esetben tipikus megoldásgörbéket, amelyek a részecskéknek adott

t

időpontbeli elmozdulását ábrázolják a részecskék láncmenti sorszámának a függvényében.
(v) Becsüljük meg, milyen lényeges változást hozna létre a körfrekvencia eloszlásában az, ha az egyik tömeget kicserélnénk egy

m' ≪ m

nagyságú tömegre.
A fenti eredmény alapján írjuk le kvalitatívan egy olyan kétatomos molekulalánc frekvenciaspektrumát, amely felváltva tartalmaz

m

és

m'

tömegű részecskéket.

Megoldás. (i) Az egyes részecskék mozgásegyenlete:

\begin{matrix} m A_{1} & = k (u_{2} - u_{1}) + k (u_{3} - u_{1}), \\ m A_{2} & = k (u_{3} - u_{2}) + k (u_{1} - u_{2}), \\ m A_{3} & = k (u_{1} - u_{3}) + k (u_{2} - u_{3}), \end{matrix}

ahol

A_{i}

i

-edik részecske gyorsulását jelöli.
(ii) Behelyettesítve az

u_{n} (t) = a_{n} \cdot cos ω t

alakú megoldást,

A_{n} = - a_{n} ω^{2} cos ω t

felhasználásával a következő egyenletrendszer adódik:

\begin{matrix} (2 ω_{0}^{2} - ω^{2}) a_{1} - ω_{0}^{2} a_{2} - ω_{0}^{2} a_{3} = 0, \\ ω_{0}^{2} a_{1} + (2 ω_{0}^{2} - ω^{2}) a_{2} - ω_{0}^{2} a_{3} = 0, \\ - ω_{0}^{2} a_{1} - ω_{0}^{2} a_{2} + (2 ω_{0}^{2} - ω^{2}) a_{3} = 0, \end{matrix}

ahol

ω_{0}^{2} = k / m

. A fenti egyenletrendszerből

a_{1}

a_{2}

és

a_{3}

kiküszöbölhető, és

ω

-ra

\begin{matrix} {(3 ω_{0}^{2} - ω^{2})}^{2} ω^{2} = 0 \end{matrix}

adódik, amelyből közvetlenül adódnak a bizonyítandó frekvenciák.
(iii)

N

részecske esetén a mozgásegyenletek

\begin{matrix} m A_{i} = k (u_{i + 1} - u_{i}) + k (u_{i - 1} - u_{i}) (i = 1, 2, ..., N) . \end{matrix}

(A periodikus határfeltétel miatt a fenti egyenletrendszerben

u_{i + N} \equiv u_{i}

, speciálisan

u_{0} \equiv u_{N}

és

u_{N + 1} \equiv u_{1}

.)
A feladat szövegében megadott megoldást a mozgásegyenletekbe helyettesítve az időtől függő tényező kiesik (ez igazolja, hogy valóban létezik ilyen alakú megoldás), s

ω_{s}^{2}

-re a következő megszorítást kapjuk:

\begin{matrix} - ω_{s}^{2} sin (\frac{2 π n s}{N} + Φ) = ω_{0}^{2} [sin (\frac{2 π (n + 1) s}{N} + Φ) - \\ - 2 sin (\frac{2 π n s}{N} + Φ) + sin (\frac{2 π (n - 1) s}{N} + Φ)] . \end{matrix}

Ennek az összefüggésnek valamennyi

n

-re ugyanazt az

ω_{s}

-t kell adnia, s ez valóban így is van, hiszen a jobb oldal az addíciós tételek felhasználásával átalakítható, s így végül az

\begin{matrix} ω_{s}^{2} = 2 \cdot ω_{0}^{2} [1 - cos \frac{2 π s}{N}] \equiv 4 ω_{0}^{2} sin^{2} \frac{s π}{N} (s = 1, 2, ..., N) \end{matrix}

eredményt kapjuk. A lehetséges frekvenciák tartománya

N \to \infty

határesetben

ω = 0

-tól

ω = 2 \sqrt[]{k / m}

-ig terjed, az előbbi az

s = 1

, az utóbbi pedig

s = N / 2

-nek felel meg. Az

s

paraméternek azért kell egész értékeket felvennie, hogy teljesüljön az

u_{i + N} (t) \equiv u_{i} (t)

feltétel.
(iv) Az

s

-edik megoldásban (az

s

-edik "módusban'')

\begin{matrix} \frac{u_{n}}{u_{n + 1}} = \frac{sin [\frac{2 π n s}{N} + Φ]}{sin [\frac{2 π (n + 1) s}{N} + Φ]} . \end{matrix}

(a) Alacsony frekvenciákon, vagyis amikor

s ≪ N

u_{n} / u_{n + 1} \approx 1

, vagyis az egymás melletti részecskék kitérése majdnem azonos.
(b) A legmagasabb frekvencia páros

N

esetén

s = N / 2

-nek felel meg, páratlan

N

-re pedig

s = \frac{N \pm 1}{2}

-hez tartozik a legnagyobb

ω

. Mindkét esetben

u_{n} / u_{n + 1} \approx - 1

vagyis az egymás melletti részecskék ellentétes irányban rezegnek (14. és 15. ábra, felül a páratlan, alul a páros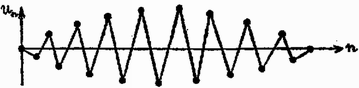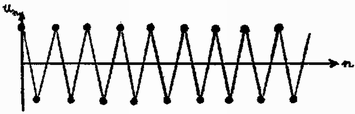

N

-ekre.)

14. ábra

15. ábra

(v) Amennyiben csak egyetlen testnél áll fenn, hogy

m' ≪ m

, úgy a könnyű test rezgésénél a nagy tömegűek elmozdulását elhanyagolhatjuk, s így rá az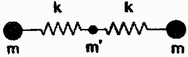

\begin{matrix} m' A = - 2 k x \end{matrix}

mozgásegyenlet érvényes (lásd a 16. ábrát).

16. ábra

Az ennek megfelelő körfrekvencia

\begin{matrix} ω' = \sqrt[]{\frac{- A}{m'}} = \sqrt[]{\frac{2 k}{m'}}, \end{matrix}

s ez kicsiny

m'

esetén sokkal nagyobb, mint

ω_{max}

.
Kétatomos lánc esetén (amely felváltva tartalmaz könnyű és nehéz részecskéket) a könnyű testek nem egyetlenegy, hanem nagyon sokféle frekvenciával mozoghatnak, ezek azonban valamennyien sokkal nagyobbak a nehéz testek rezgési frekvenciáinál. Emiatt a "frekvenciaspektrum'', vagyis a lehetséges frekvenciák ábrája két " sávra'' hasad fel, amelyeket egy tiltott tartomány, egy ún. gap (ejtsd: gep) választ el egymástól (17. ábra).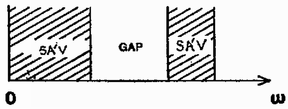

17. ábra

Gnädig Péter

Kísérleti feladatok

A mérési feladatoknál már csupán a feladatok szövege 5+12=17 gépelt oldalt tett ki. Nyilvánvalóan lehetetlenség úgy ezt, mint a megoldást teljes terjedelmében közölni. Az alábbiakban ezért csupán e feladatok rövidített szövegét, és néhány ‐ a mérések kivitelezésénél fellépő ‐ nehézséget említünk.

\begin{matrix} * \end{matrix}

A versenyzőknek két kísérleti feladatot kellett megoldaniuk, mindkettőre

2, 5

óra állt rendelkezésükre. Ezekre 100‐100 pontot, tehát összesen 200 pontot kaphattak, míg a három elméleti feladatra maximálisan 300 pontot.

1. Feladat

Az első kísérleti feladatban a versenyzőknek egy függőleges helyzetű fecskendő száján függő vízcseppen létrejövő szivárványt kellett tanulmányozniuk spektroszkóp segítségével. A fény egy 12 V-os fehér fényforrásból kollimátoron keresztül érkezett a spektroszkóp-asztal középpontja felett függő cseppre. A cseppen létrejövő szivárványt egy forgatható távcsővel kellett tanulmányozni. (18. ábra) A feladat leírása (amit a versenyzők kézhez kaptak) részletesen tárgyalta a kollimátor, a távcső, illetve a vízcsepp beállítását, továbbá a létrejövő zavaró effektusokat is (vakítóan fénylő pontok a vízcsepp felületén).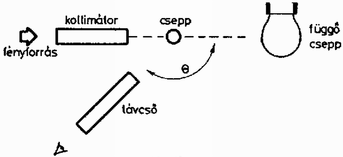

18. ábra

Tanulságosnak érezzük a szivárvány elméletével foglalkozó részt szó szerint idézni: "A lelógó csepp középső vízszintes tartománya két fénytörés és

k

számú

(k = 1, 2, ...)

belső visszaverődés eredményeképp szivárványt hoz létre. Az elsőrendű szivárvány egyetlen belső visszaverődésnek felel meg; a másodrendű kettőnek, a

k

-ad rendű pedig

k

számúnak. Valamennyi rendű szivárvány a színkép valamennyi színét tartalmazza. Ezek szabad szemmel is láthatók, a távcsővel pedig pontosan megmérheted a szögállásukat. Valamennyi szivárvány egy-egy jól meghatározott beesési szögértéknél jön létre, ez a szög mindegyik rendű szivárványnál más és más.''
A feladat részletesen foglalkozott a különböző rendű szivárványok felismerésének méréstechnikai problémáival, eligazítást nyújtva az egyes szivárványok megkereséséhez. A vizsgálatokat három különböző törésmutatójú folyadékkal kellett végezni (víz,

A

és

B

jelű folyadék), melyek törésmutatóját megadták (

n_{v} = 1, 333

n_{A} = 1, 467

n_{B} = 1, 534)

.
A versenyzőknek víz esetén szabad szemmel meg kellett figyelniük az első- és másodrendű szivárványt, továbbá mérniük kellett a távcső

Θ

elforgatási szögét a kezdeti iránytól (amikor a kollimátorból kijövő fény akadálytalanul jut a távcsőbe) az első-, a másod- és az ötödrendű szivárványok esetén. Ezekből a szögekből meg kellett határozniuk a beeső fénysugár

Φ

eltérülési szögét, vagyis azoknak a szögeknek az összegét, amelyekkel a beeső fénysugár elfordul, mialatt 2-szer megtörik és közben

k

alkalommal visszaverődik a csepp belső felületén. Ábrázolniuk kellett

Φ

értékét

k

függvényében.
Ennek a feladatnak a második részében

Φ

értékét a másodrendű szivárványokra az

A

és a

B

folyadék esetén is meg kellett határozni. Milliméterpapíron ábrázolni kellett

cos (Φ / 6)

értékét

1 / n

függvényében, ahol

n

a háromféle folyadék törésmutatója, és ezt ki kellett egészíteni egy további ponttal

n = 1

esetére. Meg kellett adni az ezekre a pontokra legjobban illeszkedő egyenes meredekségét, és végül extrapolálni

Φ

értékét az

n = 2

törésmutató esetére.
Ez a feladat a versenyzőknél kétféle nehézséggel járt. Az egyik és egyben jelentősebb méréstechnikai jellegű probléma a szivárványok helyének megtalálása volt, amit csak a csepp pontos beállításakor lehetett remélni. Ekkor viszont a sok egyszerre megjelenő szivárvány, illetve a közvetlen visszaverődésből vagy a belső visszaverődés nélküli törésekből származó vakítóan fénylő pontok zavarták az észlelést. A másik nehézséget

Φ

meghatározása jelentette, ahol észre kellett venni, hogy

Φ

értéke

360^{\circ}

-nál is nagyobb lehet abban az esetben, ha a fénysugár a vízcseppben akár többször is "körbejár''.

2. Feladat

A második kísérleti feladat nem valódi mérés, hanem egy számítógépes szimuláció nyomonkövetése volt.
A számítógépet arra programozták be, hogy az

x - y

síkban mozgó 25 darab kölcsönható részecskére megoldja a Newton-féle mozgásegyenleteket. Képes volt arra, hogy egyenlő időközökben kiszámítsa valamennyi részecske helyvektorát és sebességvektorát. Megfelelő gombok megnyomásával információt kaphattunk a rendszer dinamikai állapotáról.
A részecskék ‐ melyeket kezdetben,

t = 0

időben egy kétdimenziós négyzetrácsba rendeztek ‐ egy dobozba zárva mozoghattak. A képernyőn megjelentethető volt a rendszer állapota, a szükséges számadatokkal együtt. Ahogy a rendszer időben fejlődött, változott a részecskék helye és sebessége. (Ha egy részecske látszólag elhagyta a dobozt, a program automatikusan egy új részecskét " hozott létre'', amely a doboz ellenkező oldalán lépett be, ugyanolyan sebességgel; így a részecskék száma állandó maradt a dobozban.)
Bármely két

i

és

j

sorszámú részecske, amelyeknek egymástól mért távolsága

r_{i j}

, egy meghatározott

U_{i j}

kölcsönhatási potenciális energiával rendelkezett, a gép megfelelő utasításra kijelezte az átlagos potenciális energiát. A program továbbá arra is lehetőséget adott, hogy bármikor megkérdezhessük a számítógéptől a részecskék bármelyik sebességkomponensének akárhányadik hatványának (pl.

V_{x}

-nek vagy

V_{y}^{2}

-nek) átlagos értékét.
A "mérési'' feladatok itt a következők voltak:
1. Igazolni kellett, hogy a rendszer impulzusa (lendülete) időben állandó, megmaradó mennyiség. Becslést kellett adni a számítógép számítási pontosságára.
2‐3. Ábrázolni kellett a rendszer mozgási és potenciális energiáját az idő függvényében.
4. A rendszer teljes energiájának időbeli változását kellett megvizsgálni, s ebből az energia számítási pontosságára következtetni.
5. Kezdetben a rendszer nem volt hőmérsékleti egyensúlyban, bizonyos

t_{0}

idő után azonban beállt az egyensúly, amikor is a rendszer teljes mozgási energiája egy átlagérték körül ingadozott. Feladat volt ezen átlagérték, továbbá

t_{0}

meghatározása.
6. A megfelelő gomb lenyomására a számítógép megadta azon részecskék

Δ N

számát, amelyeknek valamelyik sebességkomponense ‐ adott pontossággal ‐

V_{0}

-lal egyezett meg. A versenyzőknek megadták, hogy hőmérsékleti egyensúlyban a "hisztogramm'' a

\begin{matrix} Δ N = A \cdot exp (- {(V_{0})}^{2} / α) \end{matrix}

alakú összefüggéssel közelíthető, ahol

α

a rendszer hőmérsékletével kapcsolatos állandó. Feladat volt a hisztogram felrajzolása, illetve

α

értékének és pontosságának meghatározása.
7. A program kívánságra megadta a részecskék ‐ valamely rögzített helytől mért ‐

Δ x

és

Δ y

elmozdulás komponenseinek négyzetátlagát. A versenyzőknek ki kellett számítani és az idő függvényében ábrázolni a részecskék átlagos elmozdulás négyzetét hőmérsékleti egyensúlyban levő rendszerre.
Igazolni kellett, hogy ez a függvény bizonyos tartományban lineáris. Az adatokból következtetni kellett arra, hogy a rendszer szilárd vagy folyékony halmazállapotú-e.

Honyek Gyula