Cím: Kristályok és kvázikristályok
Szerző(k):  Tichy Géza 
Füzet: 1986/március, 129 - 131. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kirándulásaink alkalmával gyakran találkozunk szép kristályokkal a hegyekben. Ezeket onnan ismerjük meg, hogy szemcséit síklapok határolják, és a síklapokon megtörő és visszaverődő fények adják elbűvölő csillogásukat, színeiket. Egy szemcsén belül a síklapok szöge is határozott, jellemző a kristályra. A lapok által bezárt szögek szerint a szimmetriákat figyelembe véve osztályozták a kristályokat kristályrendszerekbe.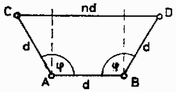
Hosszú ideig foglalkoztatta a tudósokat az, hogy miért szabályosak a kristályok, hogyan tükröződik a kristályosság az anyag mikroszkopikus szerkezetében?
A kristályos anyagban a szerkezet állandóan ismétlődik. A legkisebb ismétlődő egység állhat egy atomból, mint a legtöbb fémben (alumínium, vas, arany, réz stb.), két atomból (szilícium, gyémánt, cink, magnézium, ón, só, oparit stb.), több atomból vagy nagyobb molekulákból (cukor, kalcit, timsó, foszfor stb.). Ha gondolatban körülnézünk a kristály egy pontjából, találunk másutt is ugyanúgy kinéző pontot. Az azonosnak tűnő pontok elhelyezkedése is szabályos. Ez a szabályosság adja a sík felületeket, a meghatározott szögeket és mindent, ami a kristályok szépségét adja, ami miatt vonzódunk hozzájuk.
A só kristályait otthon is megszemlélhetjük. A szemcsék milliméter nagyságúak, a síkok szögei általában 90∘-osak, a szemcsék téglatestek. A boltban árult só szemcséit összetörték, hogy jobban szórható legyen, de még így is találhatunk benne szép szabályos szemcséket is. Ha a sót újrakristályosítjuk, szabályos szemcsékben gyönyörködhetünk.
Most megvizsgáljuk részletesebben a kristály fogalmát. Ehhez képzeljünk el egy végtelen nagy kristályt. A kristályban sok-sok olyan pont van, ahonnan a kristály ugyanúgy néz ki. Két ilyen pontot összekötő vektort eltolási vektornak nevezünk. Könnyen belátható, minden kedves olvasó elgondolkozhat rajta, hogy egy eltolási vektor bármely egészszámszorosa, illetve az eltolási vektorok összege szintén eltolási vektor. Emellett egy-egy pontból körülnézve még bizonyos szögekkel elfordulva is ugyanazt láthatjuk. Ezek a kristály forgatási szimmetriái.

 
 

Vizsgáljuk meg, milyenek lehetnek ezek a szögek. Legyen a kristályban két egyforma pont, A és B, amelyeket egy legrövidebb eltolási vektor AB köt össze. Az, hogy ez a legrövidebb ilyen vektor, azt jelenti, hogy az AB szakaszon több ilyen pont nincs (1. ábra). Az A pontban végzett φ szögű elforgatás a kristályt önmagával fedésbe hozza, ezért a C pont is ugyanolyan, mint A vagy B. Ugyanez elmondható a D pontról is, amit az A pont B körüli elforgatásával kapunk. A keletkezett CD vektornak szintén eltolási vektornak kell lennie, amely egyirányú AB-vel. Mivel AB ebben az irányban a legrövidebb, CD csak egészszámszorosa lehet AB-nek. AB hosszát d-vel jelölve, a φ szögre a következő egyenletet állíthatjuk fel:
d+2d⋅sin(φ-90∘)=nd,
amiből
cosφ=1-n2.
Ennek megoldásai:
 

n-10123φ0,2ππ3π22π3πm=2πφ16432
 

Tehát kristályos anyagban 180∘, 120∘, 90∘ és 60∘-os forgatás, azaz 2, 3, 4 és 6 forgásos szimmetriatengely lehetséges.
Ha egy anyagot valamilyen sugárzással világítunk meg, az interferenciaképből, amely kristályos anyag esetén szabályosan elhelyezkedő pontokból áll, következtetni lehet a szerkezetre. Leggyakrabban röntgen-, elektron- és neutronsugárzást használnak ilyen vizsgálathoz. Ezt az eljárást Max F. Laue fedezte fel 1912-ben. Az olyan kristályos anyagok esetében, ahol a szemcsék kicsinyek, csak az anyagok elhajlási képéből következtethetünk kristályos voltukra. Így fedezte fel Debye , hogy a fémek nagy része kristályos, bár rendszerint nagyon apró szemcséből áll.
A hullámok által létrehozott elhajlási kép szintén tartalmazza az eredeti anyag szimmetriáját, így itt is csak 2, 3, 4 és 6 forgású szimmetriatengellyel találkozhatunk.
Vannak amorf anyagok, amelyekben a részecskék rendezetlenül helyezkednek el. (Ilyen például az üveg). Az ilyen anyagról készített elhajlási kép elkent foltokból áll. Másfél éve amorf anyagok kutatása közben egy washingtoni kutatóintézet munkatársai megdöbbentő eredményt kaptak. Alumíniumot ötvöztek magánnal 6:1 arányban, és az ötvözet olvadékát hideg réztömbre freccsentették, ami így gyorsan lehűlt. A gyors lehűtéstől rendezetlen, nem kristályos amorf anyagot vártak, ahogy ezt sok más ötvözet esetében tapasztalták. Az elektronsugárral végzett elhajlási kísérletek azonban furcsa képet mutattak. A képen szabályosan elhelyezkedő pontok voltak, ami kristályos anyagra utalt, azonban ezek a pontok tízforgású szimmetriát mutattak. Ez nem egyeztethető össze a kristályos anyagok tulajdonságaival. Azóta ezt a kísérletet többször megismételték, hazánkban az Eötvös Loránd Tudományegyetem Szilárdtest Fizika Tanszéke állított elő ilyen anyagot.
A fizikusokat erősen foglalkoztatja az a kérdés, milyen lehet a szerkezete ennek az anyagnak. Az atomok pontos elrendeződését még nem sikerült meghatározni, de már sokat tudunk róla. Az elrendeződés nem lehet periodikus, mint egy kristályban, de valamilyen rendnek kell benne lennie. Ezt mutatják az elhajlási képek.
Ennek a szerkezetnek a magyarázatára alkották meg a kvázikristály fogalmát. (Kvázi a latin quasi szó magyar változata, jelentése ,,mintha''.) A kvázikristály nem kristály, de olyan, mintha kristály lenne. Míg a kristályban vannak olyan pontok, ahonnan a kristály ugyanúgy néz ki, itt csak hasonló pontok vannak, teljes ismétlődés nincs.
A kristályos anyag teljesen azonos építőkövekből, szerkezeti egységekből áll. A kvázikristály kettő vagy több szerkezeti egységből tehető össze. Példaként nézzünk meg egy kétdimenziós kvázikristályt, a Penrose szerkezetet! Vágjunk ki papírból kétfajta, azonos élhosszúságú rombuszokat! Az egyik szöge legyen 72∘, a másiké 36∘. Ezekkel a rombuszokkal lefedhetjük a síkot. A lefedés mindig folytatható, a kapott szerkezet sosem lesz periodikus, de megfelelő tartományai nagyon hasonlóak.
Egy kvázikristályos szerkezetet mutat a hátsó borítón látható ábra is. Ennek szimmetriái megfelelnek egy Penrose rács szimmetriáinak. A kép az alábbi BASIC programmal egy Macintosh számítógépen készült. A PSET utasítás befeketíti a képernyő megfelelő pontját.
 
 
A hátsó borító ábrája
 

A rácsot úgy szerkesztettük, hogy az elhajlási képe tízforgású legyen.
 

  10  DIM kx(5),ky(5):pi=4*ATN(1)  20  CLS  30  FOR i=1 TO 5  40  kx(i)=COS(.4*pi*i)    50  ky(i)=SIN(.4*pi*i)    60  NEXT i  70  FOR ix=-250  TO 250  80  FOR iy=-150  TO 150  90  f=0  100  FOR i=1 TO 5  110  f=f+COS(kx(i)*ix+ky(i)*iy)  120  NEXT i  130  IF f >0 GOTO 150  140  PSET(ix+250, iy+150)  150  NEXT iy,ix  160  STOP
 

Az Al6Ma szerkezetét is kirakhatjuk kétféle idomból. Ehhez kétfajta romboédert állítunk elő, egy kövéret és egy soványat. A romboéder hat rombusz által határolt test. A rombuszok szögei 63,43∘, illetve 106,67∘-os. Ezek azok a szögek, amelyek tangense kettő. A sovány romboéderben egy csúcsban három 63,43∘,-os csúcs találkozik, a kövérben három 106,67∘-os. Ebből a két testből ki lehet rakni a teret, bár nem periodikusan. A kirakást bárki megpróbálhatja.
A kutatók megint új anyagot állítottak elő. Egy lényegesen új anyag lényegesen új tulajdonságokkal is rendelkezhet. Mivel ebből az anyagból csak kis szemcsék vannak más szerkezetű alumínium-mangán ötvözetek között, tulajdonságait még nem ismerjük. További kutatások adnak majd választ arra a kérdésre, hogy ennek az érdekes szerkezetnek milyen új tulajdonságai vannak, amelyek majd meghatározzák a kvázikristályok felhasználási területét.
 

 Tichy Géza, egyetemi docens
 Budapest, ELTE