Kezdőlap


Cím:	1986. Az XXVII. Nemzetközi Matematikai Diákolimpia feladatainak megoldása
Füzet:	1986/november, 355 - 360. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Feladat. Legyen $d$ $2$ -től, $5$ -től és $13$ -tól különböző pozitív egész szám. Bizonyítsuk be, hogy a ${2, 5, 13, d}$ halmaznak van két különböző $a$ , $b$ eleme, amelyre $a b - 1$ nem négyzetszám.

Megoldás. Elegendő belátni a következő állítást: ha

d

pozitív egész szám, akkor a

2 d - 1

5 d - 1

és

13 d - 1

számok közül valamelyik nem négyzetszám. Tegyük fel ugyanis ennek ellenkezőjét, vagyis hogy alkalmas

a

b

c

pozitív egész számokkal

\begin{matrix} 2 d - 1 & = a^{2} & (1) \\ 5 d - 1 & = b^{2} & (2) \\ 13 d - 1 & = c^{2} . & (3) \end{matrix}

(1)-ből leolvasható, hogy

a

páratlan. Ekkor

a^{2}

4-gyel osztva 1-maradékot ad, és így

d

is páratlan. Most (2)-t és (3)-at tekintve adódik, hogy

b

és

c

páros. Vonjuk le (3)-ból (2)-t:

\begin{matrix} 8 d = c^{2} - b^{2}, & (4) \\ 2 d = \frac{c + b}{2} \cdot \frac{c - b}{2} . & (5) \end{matrix}

b

és

c

közül egyik 4-gyel osztható, másik pedig 2 maradékot ad 4-gyel osztva, akkor (5) jobb oldalának mindkét tényezője páratlan, ez tehát nem lehet. Ha viszont

b

és

c

4-gyel osztva ugyanazt a maradékot adja, akkor (5) mindkét tényezője páros, amiből

d

páros volta következik. Ez az ellentmondás igazolja állításunkat.
(Benczúr András)

2. feladat. Adott az

A_{1} A_{2} A_{3}

háromszög és a síkjában levő

P_{0}

pont. Definiáljuk

s > 4

esetén az

A_{s}

pontot így:

A_{s} = A_{s - 3}

. A

P_{n + 1}

pontot úgy nyerjük, hogy a

P_{n}

pontot

A_{n + 1}

körül az óramutató járásával megegyező irányban

120^{\circ}

-kal elforgatjuk. Bizonyítsuk be, hogy ha

P_{1986}

és

P_{0}

megegyező pontok, akkor az

A_{1} A_{2} A_{3}

háromszög szabályos.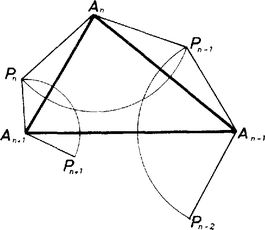

Megoldás. Vizsgáljuk meg először azt, hogy három egymást követő elforgatás során mi történik az

\vec{A_{1} P_{0}}

vektorral. Bármelyik elforgatás a vektor irányát

120^{\circ}

-kal változtatja, hosszát pedig megtartja. Így ha a három elforgatás utáni

\vec{A'_{1} P_{3}}

képét tekintjük, akkor

\vec{A_{1} P_{0}} = \vec{A'_{1} P_{3}}

adódik. Tehát

A_{1} P_{0} P_{3} A'_{1}

négyszög paralelogramma,

\vec{P_{0} P_{3}} = \vec{A_{1} A'_{1}}

. Hasonló gondolatmenettel adódik

\vec{P_{3} P_{6}} = \vec{A_{1} A'_{1}}

, általában

\vec{P_{3 k} P_{3 k + 3}} = \vec{A_{1} A'_{1}}

minden

k

természetes számra. Ezért

\vec{P_{0} P_{1986}} = = \vec{P_{0} P_{3}} + \vec{P_{3} P_{6}} + ... + \vec{P_{1983} P_{1986}} = 662 \cdot \vec{A_{1} A'_{1}}

, tehát, mivel

P_{0} = P_{1986}

\vec{P_{0} P_{1986}}

és így

\vec{A_{1} A'_{1}}

is nullvektor, vagyis

A_{1}

megegyezik

A'_{1}

-vel.
Most kövessük nyomon azt, hogyan nyerjük

A'_{1}

-t

A_{1}

-ből. Az

A_{1}

körüli elforgatás helyben hagyja

A_{1}

-et, majd az

A_{2}

körüli

120^{\circ}

-os elforgatás

A''_{1}

-be viszi.

A''_{1}

-t pedig az

A_{3}

körüli (az előzővel megegyező irányú) elforgatás viszi

A_{1} = A'_{1}

-be. Ezért

A_{1} A_{2} A''_{1} A_{3}

négyszög rombusz, melynek

A_{2}

-nél levő szöge

120^{\circ}

-os, így

A_{1}

-nél

60^{\circ}

-os szöge van. Tehát az

A_{1} A_{2} A_{3}

háromszög, melynek

A_{1} A_{2}

és

A_{1} A_{3}

oldalai egyenlők, valóban szabályos.
(Lipták László)

3. feladat. Egy szabályos ötszög csúcsaihoz egy-egy egész számot rendelünk úgy, hogy összegük pozitív legyen. Megengedett a következő művelet: ha három szomszédos csúcs

X

Y

Z

és a hozzájuk rendelt számok

x

y

z

, és

y < 0

, akkor az

x

y

z

számok helyére ugyanilyen sorrendben az

x + y

- y

z + y

számokat írjuk. Ezt a műveletet ismételgetjük addig, amíg csak található negatív

y

. Döntsük el, vajon minden esetben véget ér-e az eljárás véges sok lépés után!

Megoldás. Az eljárás véges sok lépés után minden esetben véget ér, függetlenül attól, hogy milyen sorrendben végezzük el a lépéseket. Legyen az ötszög csúcsaihoz rendelt öt szám kezdetben

a_{0}

b_{0}

c_{0}

d_{0}

e_{0}

, az

n

-edik "művelet'' elvégzése után pedig

a_{n}

b_{n}

c_{n}

d_{n}

e_{n}

. Világos, hogy bármely lépés után a számok egészek maradnak, és összegük nem változik, tehát pozitív marad. Definiáljuk az

S_{n}

nem-negatív egész számot így:

\begin{matrix} S_{n} = {(a_{n} - c_{n})}^{2} + {(b_{n} - d_{n})}^{2} + {(c_{n} - e_{n})}^{2} + {(d_{n} - a_{n})}^{+} {(e_{n} - b_{n})}^{2} . \end{matrix}

Ha valamely

k

természetes számra az

a_{k}

b_{k}

c_{k}

d_{k}

e_{k}

számok között van negatív (mondjuk

c_{k} < 0

), akkor a következő lépés után nyert

a_{k + 1} = a_{k}

b_{k + 1} = b_{k} + c_{k}

c_{k + 1} = - c_{k}

d_{k + 1} = d_{k} + c_{k}

e_{k + 1} = e_{k}

számokra

S_{k + 1} < S_{k}

. Ugyanis behelyettesítéssel

\begin{matrix} S_{k + 1} - S_{k} = 2 c_{k} (a_{k} + b_{k} + c_{k} + d_{k} + e_{k}), \end{matrix}

és itt

c_{k} < 0

a_{k} + b_{k} + c_{k} + d_{k} + e_{k} > 0

, mint azt már említettük. Ez pedig azt jelenti, hogy

S_{0}

S_{1}

S_{2}

...

szigorúan csökkenő nem negatív egész számok. Így sorozatuk csak véges hosszúságú lehet, vagyis az eljárás véges sok lépésben mindig véget ér.

(Kós Géza)

4. feladat. Legyenek

A

és

B

egy

O

középpontú szabályos

n

-szög

(n \geq 5)

szomszédos csúcsai. Egy, az

O A B

háromszöggel egybevágó

X Y Z

háromszöggel először befedjük

O A B

-t, majd az

X

pontot úgy mozgatjuk ‐ mindig az

n

-szög belsejében ‐, hogy eközben az

Y

és

Z

pontok állandóan az

n

-szög oldalain legyenek. Milyen alakzatot ír le

X

, ha

Y

befutja az

n

-szög határát (kerületét)?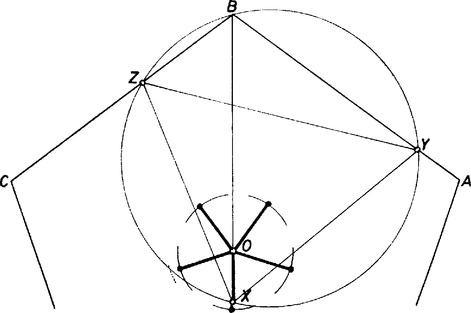

Megoldás. Állítjuk, hogy a keresett ponthalmaz

n

darab zárt szakaszból áll, amelyek hossza

O B (\frac{1}{cos \frac{π}{n}} - 1)

, és amelyek az

n

-szög csúcsait

O

-val összekötő szakaszok

O

-n túli meghosszabbításai.
Ha

Y

és

Z

két szomszédos csúccsal esik egybe, akkor

X \equiv O

; a többi esetben

X

két szomszédos oldal által határolt kisebbik szögtartományban helyezkedik el (ennek igazolásától most eltekintünk).
Legyen most

Y

A B

Z

pedig a vele szomszédos

B C

oldal belső pontja. Ekkor

Y B Z ∢ = A B C ∢ = π - \frac{2 π}{n}

Y X Z ∢ = \frac{2 π}{n}

, e két szög összege tehát

π

, vagyis az

X Y B Z

négyszög húrnégyszög. Mivel

X Y = X Z

, az

X B Y

és

X B Z

szögekhez egyenlő ívek tartoznak, ezért

X B Y ∢ = X B Z ∢

; az

X

pont az

Y B Z ∢ = A B C ∢

szögfelezőjén helyezkedik el.
Vizsgáljuk most meg, mekkora lehet a

B Z

távolság! Először belátjuk, hogy

B X > O B

. Ugyanis

X Y B ∢ + X Z B ∢ = π

, így közülük az egyik legalább

\frac{π}{2}

, mondjuk

X Z B ∢ \geq \frac{π}{2}

. De

X B Z ∢ < \frac{π}{2}

, ezért az

X Z B

háromszögben ezen szögekkel szemben fekvő oldalakra

B X > X Z

adódik

X Z B ∢ > X B Z ∢

miatt. És itt

X Z = O B

. Másodszor

B X

szakasz hosszára felső becslés az

X Y B Z

húrnégyszög köré írható kör átmérője. Ez pedig a szinusztétel segítségével

\begin{matrix} \frac{Y Z}{sin Y X Z ∢} = \frac{O B}{sin (\frac{π}{2} - \frac{π}{n})} = \frac{O B}{cos \frac{π}{n}} . \end{matrix}

Ehhez hozzávéve a megoldás elején említett

X \equiv A

Y \equiv B

Z \equiv O

esetet,

\begin{matrix} 0 \leq O X \leq \frac{O B}{cos \frac{π}{n}} - O B = O B (\frac{1}{cos \frac{π}{n}} - 1) \end{matrix}

adódik. Ha pedig gondolatmenetünket elvégezzük a többi szomszédos oldalpárra is, akkor kiderül, hogy

X

csakis a megoldás elején leírt ponthalmaz pontja lehet.
Hátravan még annak igazolása, hogy az említett halmaz minden pontja megfelelő. Legyen

X'

B O

félegyenesen úgy, hogy

O B < B X' \leq \frac{O B}{cos \frac{π}{n}}

. Rajzoljuk meg a

B

-n és

X'

-n átmenő,

\frac{O B}{cos \frac{π}{n}}

átmérőjű körök valamelyikét (ha

B X' = \frac{O B}{cos \frac{π}{n}}

, akkor csak egy ilyen van). Az olvasóra bízzuk annak igazolását, hogy ez a kör metszi az

A B

és

B C

szakaszokat. Jelöljük ezen metszéspontokat

Y'

-vel és

Z'

-vel. Mivel

Y' B X' ∢ = X' B Z' ∢

, azért

X' Y' = X' Z'

. Másrészt mivel

X' Y' B Z'

négyszög húrnégyszög,

Y' X' Z' ∢ = π - Y' B Z' ∢ = \frac{2 π}{n}

. Ezért az

X' Y' Z'

háromszög hasonló az

A B O

háromszöghöz, körülírt köreik pedig ugyanakkorák, ezért a két háromszög egybevágó. Ez a meggondolás bizonyítja, hogy a megadott ponthalmaz minden pontja jó.

(Kós Géza)

5. feladat. Határozzuk meg az összes olyan

f

függvényt, amely a nem‐negatív valós számok

R_{0}^{+}

halmazán van értelmezve, csak nem‐negatív valós értéket vesz fel és teljesíti a következő három feltételt:

\begin{matrix} (a) f (x \cdot f (y)) \cdot f (y) = f (x + y) minden x, y \in R_{0}^{+} esetén; \\ (b) f (2) = 0; \\ (c) f (x) \neq 0, ha 0 \leq x < 2. \end{matrix}

Megoldás. Először két egyszerű megállapítást teszünk. Egyrészt

f (0) = 1

, hiszen az (a) feltételt

x = y = 0

esetén alkalmazva

f (0) = f (0 \cdot f (0)) \cdot f (0) = = f {(0)}^{2}

, tehát

f (0)

értéke csak 0 vagy 1 lehet, de az első lehetőséget a (c) feltétel kizárja. Másrészt

x \geq 2

esetén

f (x) = 0

adódik könnyen, ha az (a) feltételbe

x - 2

és 2 értékeket írunk:

f (x) = f ((x - 2) \cdot f (2)) \cdot f (2) = 0

a (b) feltétel miatt.
Tegyük fel most, hogy

0 < x < 2

, ekkor persze

0 < 2 - x < 2

is teljesül, és így az (a) feltételt alkalmazva a

2 - x

és

x

számokra

f ((2 - x) \cdot f (x)) \cdot f (x) = f (2) = O

adódik. Itt (c) miatt

f (x) \neq 0

((2 - x) \cdot f (x)) = 0

, tehát ismét csak (c)-t alkalmazva a

(2 - x) \cdot f (x) \geq 2

(x) \geq \frac{2}{2 - x}

egyenlőtlenséget kapjuk. A továbbiakban belátjuk, hogy itt egyenlőség áll. Tegyük fel ugyanis, hogy valamely

0 < y < 2

esetén

f (y) > \frac{2}{2 - y}

, vagyis

f (y) = \frac{2}{2 - y} + d

, ahol

d

pozitív. Ekkor található olyan

x

pozitív szám, melyre

\frac{2}{f (y)} = \frac{2}{\frac{2}{2 - y} + d} < x < < 2 - y

. Erre az

x

y

párra

x + y < 2

, tehát

f (x + y) > 0

; valamint

x \cdot f (y) > 2

f (x \cdot f (y)) = 0

áll fenn. Így az (a) feltétel nem teljesül rájuk, és ez az ellentmondás mutatja, hogy valóban minden

0 < y < 2

esetén

f (y) = \frac{2}{2 - y}

. Az eddigiek során tehát megállapítottuk, hogy a feladat feltételeinek csak a következő függvény tehet eleget:

\begin{matrix} f (x) = {\begin{matrix} \frac{2}{2 - x} ha 0 \leq x < 2 \\ 0 ha x \geq 2. \end{matrix} \end{matrix}

Most már csak azt kell megvizsgálnunk, hogy ez a függvény valóban megfelel-e a követelményeknek. Ezt azonban az olvasóra bízzuk, könnyen látható, hogy ez a függvény jó.

(Bóna Miklós)

6. feladat. Adott a síkban egy véges sok rácspontból álló halmaz. Döntsük el, vajon minden esetben lehetséges-e ezek közül a pontok közül néhányat pirosra, a többit pedig fehérre színezni úgy, hogy minden olyan egyenesen, amely párhuzamos valamelyik koordináta‐tengellyel, a rajta lévő piros pontok száma legfeljebb

1

-gyel térjen el az ugyancsak rajta lévő fehér pontok számától.

Megoldás. A pontok számára vonatkozó teljes indukcióval bebizonyítjuk, hogy mindig létezik a kívánt színezés. Egy pont esetén az állítás nyilvánvaló. Tegyük fel tehát, hogy

n \geq 2

, és

n

-nél kevesebb pont esetén kiszínezhetők a pontok az előírt módon, és megadjuk az

n

pontnak egy megfelelő színezését.
Könnyű dolgunk van, ha található olyan

P

pont, melynek sorában további pont már nincs. Ekkor

P

-t elhagyva a megmaradt (

n - 1

) pontot színezzük ki a megfelelő módon, és ha

P

oszlopában legalább annyi piros pont van, mint fehér, akkor

P

-t színezzük fehérre, ha eggyel több fehér pont van, mint piros, akkor pedig pirosra. Ekkor az

n

pontnak egy jó színezését kaptuk, hiszen

P

sorában és oszlopában teljesül a feltétel, a többi sorban és oszlopban pedig nem történt változás. Hasonló a helyzet, ha van olyan

P

pont, melynek oszlopában nincs további pont. Vizsgáljuk tehát azt a fennmaradó esetet, amikor minden pont sorában és oszlopában is van további pont. Ekkor egy tetszőleges

A_{1}

pontból kiindulva, annak sorában választhatunk egy tőle különböző

A_{2}

pontot,

A_{2}

oszlopában

A_{3}

-t,

A_{3}

sorában

A_{4}

-t, és így tovább felváltva. Minthogy véges sok

(n)

pontunk van, véges sok lépés után az

A_{1}

A_{2}

...

pontsorozatban olyan tagot kell választanunk, amely már szerepelt. Legyen tehát

A_{r} = A_{p} (r > p)

az első ilyen ismétlődés. Ha

r - p

páros, akkor az

A_{p}

A_{p + 1}

...

A_{r - 1}

sorozatban minden tag az egyik szomszédjával egy sorban, a másikkal egy oszlopban van (ha

A_{r - 1}

-t és

A_{p}

-t is szomszédoknak tekintjük). Gondoljunk utána, hogy ha

r - p

páratlan, akkor ugyanez mondható az

A_{p + 1}

A_{p + 2}

...

A_{r - 1}

sorozatról. Hagyjuk el tehát ezen sorozat pontjait, a maradékot az indukciós feltétel szerint kiszínezhetjük a kívánt módon, a sorozat pontjait pedig színezzük ezután felváltva pirosra, ill. fehérre. Ekkor az

n

pontnak egy jó színezését kapjuk, hiszen minden sorban és oszlopban ugyanannyival változtatjuk meg a piros, ill. fehér pontok számát. Ezzel az indukciós lépést elvégeztük, a feladat kérdésére igenlő választ adhatunk.

(Tóth Géza)