|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. A konvex -szöget egymást nem metsző átlóval háromszögre bontottuk. Bizonyítsuk be, hogy a háromszögek megszámozhatók az , , , számokkal úgy, hogy , , , -re az sorszámú háromszögnek valamelyik csúcsa legyen.
I. megoldás. A feladat állítását teljes indukcióval bizonyítjuk. Ha , akkor a háromszöget kell az számmal megszámozni, és ez lehetséges, mégpedig egyféleképpen.
Tegyük most fel, hogy -re igaz a tétel, vagyis egy háromszögekre bontott, konvex -szög háromszögeit meg lehet számozni a kívánt módon. Legyen egy konvex -szög, amelyiket egymást nem metsző átlók háromszögekre bontanak. Hagyjuk el a csúcsot, és a belőle induló szakaszok helyett húzzuk meg a szakaszokat. Ezzel a sokszög egy felosztását kaptuk átlók útján. Ezek az átlók sem metszhetik egymást, mert azok az átlók, amelyek az eredeti sokszögben is meg voltak húzva, nem metszik egymást, egy olyan átló pedig, amelyik egy átló helyébe lépett, csak olyan átlót metszhetne át, amelyiknek egyik végpontja és közt van, ide azonban nem esik csúcsa egyik sokszögnek sem.
Az új átlók a -szöget háromszögekre bontják. Az eredeti sokszögnek azok a részháromszögei ugyanis, amelyeknek nem csúcsa , szerepelnek a -szög felbontásában is. Az eredeti sokszögben van egy háromszög, ezt összehúztuk a átlóra, a háromszögek helyébe pedig, ha , a háromszögek lépnek. Ezek együtt hézag és átfedés nélkül kitöltik a sokszöget. Ezek a háromszögek az indukciós feltevés szerint megszámozhatók a kívánt módon az , , , számokkal.
Ezután a -szög felbontásában azok a háromszögek, amelyek a -szög felbontásában is szerepelnek, tartsák meg sorszámukat. Ha , és ha a háromszög fellép, akkor kapja azt a sorszámot, amit a -szög felbontásában a háromszög kapott (ez i vagy j). Végül a háromszögnek a sorszám jut. Világos, hogy így minden háromszögnek van a sorszámával egyező indexű csúcsa. A -szög háromszögei is megszámozhatók tehát a kívánt módon.
Megjegyzések. 1. A bizonyítás menetét követve az is belátható, hogy mindig csak egyféleképpen végezhető el a háromszögek megszámozása a követelményeknek megfelelően.
2. Abból a feltételből, hogy egy konvex -szöget egymást nem metsző átlók háromszögekre bontanak, következik, hogy átlóval háromszögre van felosztva a sokszög. Valóban, minden átló meghúzása 1-gyel növeli a részsokszögek számát, a részsokszögek oldalainak együttes száma pedig 2-vel szaporodik, mert a korábbi oldalakon kívül a meghúzott átló is oldala lesz két sokszögnek. Ha tehát átló meghúzása után csupa háromszög keletkezett, akkor egyfelől háromszög keletkezett oldallal, másfelől a keletkezett részsokszögek oldalainak együttes száma . Ebből következik állításunk. Ezeknek a részadatoknak a kiszámítása azonban fölöslegesen terhelte volna a megoldásra rendelkezésre álló időt.
3. Más lehetőségek is kínálkoztak indukciós bizonyításra. Ezeket csak röviden jelezzük.
a) Fogalmazzuk az indukciós feltételt úgy, hogy a -nál kisebb -ekre igaz az állítás. Egy -szög felbontásában szerepel egy háromszög. Ennek a sorszámot kell kapnia. Maradt két -nál nem több oldalú sokszög, vagy esetleg csak egy, ezeknek a háromszögeit az indukciós feltevés felhasználásával meg tudjuk a kívánt módon számozni.
b) Könnyen látható, hogy és legalább egyikéből indul ki átló. Egy ilyennel két részsokszögre bontva, azok részháromszögei az indukciós feltétel felhasználásával megszámozhatók a kívánt módon.
c) Többen azt bizonyították be, hogy van legalább két olyan csúcs, amelyikből nem indul ki átló. Ennél valamivel többet is állíthatunk. Egy ilyen "átlómentes'' csúccsal szomszédos csúcsokat átlónak kell összekötnie, ha a sokszög háromszögekre van bontva (amiből következik az is, hogy két szomszédos csúcs nem lehet egyszerre átlómentes). Nevezzük a keletkező háromszöget szélsőnek és jelöljük a szélső háromszögek számát -sel. Ezeknek két oldala sokszögoldal, a harmadik átló. Lesz olyan háromszög, amelyiknek egy oldala sokszögoldal, kettő átló, és lehetnek olyan háromszögek is, amelyeknek mindegyik oldala átló. Az utóbbiak számát jelöljük -vel Ekkor | |
az átlók kétszeres számát adja, vagyis -et. Innen adódik, vagyis a szélső háromszögek száma 2-vel nagyobb a "belső'' háromszögekénél, tehát legalább 2.
Két szélső háromszög "középső'' (átlómentes) csúcsa közül legalább az egyik különbözik -tól is, -től is. Egy ilyen háromszög csak a középső csúcs sorszámát kaphatja. Egy ilyen háromszöget elhagyva a maradó sokszög háromszögeit meg tudjuk számozni az indukciós feltétel alapján a kívánt módon.
Adhatunk közvetlen utasítást is a háromszögek megszámozására.
II. megoldás. Adjuk a felosztásban szereplő háromszögnek, ha , a számot. Ezzel minden háromszög kapott számot. Az is világos, hogy mindegyiknek a száma legalább és legfeljebb . Elég tehát még azt belátni, hogy két háromszög nem kaphatta ugyanazt a sorszámot.
Ha a fenti háromszögön kívül még valamelyiknek csúcsa , akkor ennek nem lehet csúcsa a sokszög kerületének -tól -on át -ig menő részén, mert az azt -vel összekötő átló metszené -t. Nem lehet egy ilyen háromszögnek egy csúcsa a kerület részén, egy pedig a részen, mert az ezeket összekötő átló metszené -t is, -t is. Ekkor azonban a kérdéses háromszögnek vagy legkisebb indexű csúcsa, vagy a legnagyobb indexű, s így a háromszög -től különböző sorszámot kap. Ezzel a feladat állítását bebizonyítottuk.
Megjegyzés. A feladat állítása igaz marad akkor is, ha tetszés szerinti sorrendben írjuk a csúcsok mellé a , , , sorszámokat. Ha egy ilyen sorszámozás mellett és szomszédosak, akkor könnyen látható, hogy az állítás nem lényegesen más, mint az eredeti. Tegyük tehát fel, hogy nem szomszédosak. Ismét teljes indukcióval bizonyítunk.
Ha , akkor és átellenes csúcsok. Ha a négyszög a átlóval van kettéosztva, akkor nyilván a háromszögnek kell az 1 számot kapnia, a másiknak a 2-t. Ha viszont a átló van meghúzva, akkor bármelyik háromszög kaphatja az 1-et és a másik a 2-t.
Tegyük fel, hogy az állítás igaz a legfeljebb oldalú sokszögekre és legyenek egy háromszögekre bontott -szög csúcsai tetszés szerinti sorrendben -val jelölve, de és ne legyen szomszédos. Ha szerepel az átlók között, akkor ez két olyan sokszögre osztja a -szöget, amelyek külön-külön eleget tesznek a feladat feltételeinek (csak itt már két szomszédos csúcs az, amelyeknek az indexét nem használhatjuk fel a háromszögek számozásánál), ezek háromszögei tehát megszámozhatók az indukciós feltevés szerint a kívánt módon. Ha a átló nincs meghúzva, akkor legyen és a legközelebbi csúcs két oldalán, amelyik össze van kötve -val. Mivel a sokszög háromszögekre van bontva, a átlónak szerepelnie kell a kijelölt átlók közt. Vágjuk ketté ezzel a -szöget, és a -t tartalmazó sokszögben zárjuk még ki az -t, a -t tartalmazó sokszögben a -t a háromszögek számozására megengedett értékek közül. Ekkor a részsokszögek háromszögei megszámozhatók az indukciós feltétel szerint a kívánt módon, és ez a számozás megfelelő lesz a -szögre is, mivel a -t tartalmazó sokszögben -t, a -t tartalmazóban pedig -t felhasználtuk számozásra.
2. Minden természetes számhoz vegyük prímszám osztóinak a legnagyobb hatványát, amelyik még nem nagyobb -nél, és ezek összegét nevezzük az -hez tartozó hatványösszegnek. (Pl. a -hoz tartozó hatványösszeg ). Bizonyítsuk be, hogy végtelen sok olyan szám van, amelyikhez tartozó hatványösszeg nagyobb a számnál.
A versenyzők igen változatos számsorozatokat adtak meg. A legegyszerűbb talán a következő.
Megoldás. A számok, ahol 1-nél nagyobb egész szám, megfelelnek. Valóban, 2-nek nyilván a -adik hatványa szerepel a hatványösszegben; továbbá van a számnak legalább egy páratlan prím osztója, mert a szám fele 1-nél nagyobb páratlan szám. Igy a hatványösszeg legalábbis , ami nagyobb -nél.
Megjegyzés. Az olvasóra bízzuk annak belátását, hogy a következő számsorozatok is megfelelnek:
, ahol egy (rögzített) páratlan prímszám, pedig pozitív egész.
, .
6-nak a 2 hatványait követő legkisebb többszörösei. Hasonlóan megfelelnek 10-nek a 2 ötödiknél magasabb hatványait követő többszörösei is.
A páratlan prímszámok kétszeresei. Itt természetesen felhasználjuk már azt, hogy végtelen sok prímszám van (és ezek a 2 kivételével páratlanok).
A 30 többszörösei.
Az utolsó választás megfelelő volta abból adódik, hogy ha egy szám osztható a prímszámmal, és a hatványösszegben szerepel, ez azt jelenti, hogy Innen
Ha tehát osztható 30-cal, akkor a 2, 3 és 5 adaléka a hatványösszeghez több, mint
Ismeretes az is, hogy a prímszámok reciprok értékeinek az összege tetszés szerinti nagy lehet, ha elég sok prímszámot veszünk. Ez esetünkben azt is adja, hogy a hatványösszeg nemcsak a számnál, hanem annak tetszés szerint adott többszörösénél is végtelen sok számra nagyobb lehet.
3. Egy háromszög csúcsait tükröztük a velük szemközti oldalegyenesekre. Bizonyítsuk be, hogy az így kapott három pont által alkotott háromszög területe kisebb az eredeti háromszög területének ötszörösénél.
A feladat megoldását, azon túl, hogy nem könnyű alkalmas kifejezést találni a kérdéses terület meghatározására, nehezíti az is, hogy nem elegendő egy ábrára hagyatkozni, lényeges, hogy minden lehetséges esetre gondoljunk. Több ábrát rajzolva feltűnik az is, hogy ha a háromszög egyik szöge nagyobb -nál, akkor a tükrözéssel keletkezett háromszög körüljárási iránya ellentétes az eredetiével. Ezért célszerű lesz előjeles területtel számolni, mint az a koordináta-geometriában szokásos.
I. megoldás. Egy háromszög területét tekintsük pozitívnak vagy negatívnak aszerint, amint a háromszöget a csúcsok megadott sorrendje szerint körüljárva, az óramutató járásával ellentétes vagy azzal egyező irányban haladunk.
 1. ábra
Ekkor végignézve a lehetséges eseteket (1 . ábra) látjuk ‐ a háromszögek területét ugyanúgy jelölve, mint magát a háromszöget ‐ , hogy a háromszög síkjának egy tetszés szerinti pontjára fennáll a következő összefüggés:
Ha valamelyik három pont egy egyenesre esik, akkor a keletkező, egyenesszakasszá fajult "háromszög'' területén természetesen 0-t értünk.
Feladatunkra térve legyen egy tetszés szerinti háromszög pozitív körüljárásnak megfelelően betűzve. Jelöljük a csúcsok tükörképeit a velük szemközti oldal egyenesére rendre , , ill. -gyel (2. ábra).
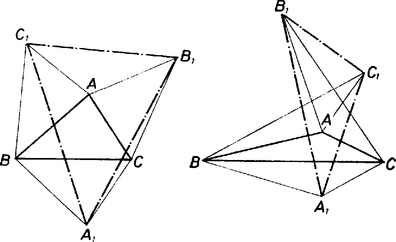 2. ábra
Az háromszög területét az eredeti háromszögével, tükörképeiével, továbbá az , , oldalakhoz csatlakozó egy-egy háromszög területével akarjuk kifejezni. Ehhez alkalmazzuk először (1)-et az háromszögre, -nak az pontot választva: | |
Alkalmazzuk most (1)-et a jobb oldal első és harmadik tagjára, -nak -t, ill. -t választva:
Végül még a négyszöget kellene az eredeti háromszögre és tükörképére bontani. Ehhez alkalmazzuk (1)-et pl. a háromszögre, -nak -t választva:
Adjuk össze egyenleteink bal és jobb oldalait, hagyjuk el a mind a két oldalon előforduló tagokat, továbbá a és tagokat, mert ezek összege 0, hiszen ugyanannak a háromszögnek a területéről van szó egyszer pozitív, egyszer negatív előjellel. Így a következő egyenlőséghez jutottunk: | |
Itt az utolsó előtti tag az eredeti háromszög területe és vele egyenlő a harmadik, a negyedik és az utolsó tag is. Ezek ugyanis a tükrözött háromszögek területei. A tükrözés ugyan megváltoztatja a körüljárás irányát, de mindhárom esetben megfordult a betűzés sorrendje is.
Meg kell még vizsgálnunk a fennmaradt háromszögeket. Ezeknek egy-egy csúcsa közös az eredeti háromszöggel, és a körül az eredeti háromszög megfelelő szögének a háromszorosa keletkezik, de hol a háromszögön belül, hol azon kívül. Az ebből a csúcsból induló oldalak az eredeti háromszög egy-egy oldalával egyenlők. Vizsgáljuk meg közelebbről pl. az háromszöget.
Az oldalakra
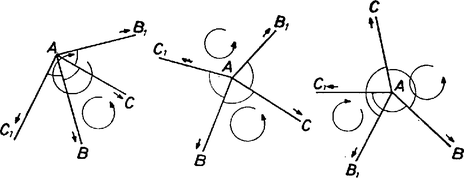 3. ábra
A közbezárt szögre ‐ jelöléssel ‐ aszerint, hogy és , vagy és , vagy és közé esik, a értéke (3. ábra) , , ill. . A háromszög kétszeres területét mint két oldalnak és a közbezárt szög szinuszának a szorzatát írva, abszolút értékére a három esetnek megfelelően | |
ill. | |
adódik.
A háromszög körüljárási iránya viszont éppen a második esetben pozitív, az elsőben és a harmadikban negatív, így előjellel is helyesen adja meg a háromszög területét mind a három esetben a egyenlőség. Természetesen a megfelelő egyenlőség érvényes a másik két háromszögre. Jelöljük az eredeti háromszög területét -vel, a tükrözéssel keletkezettét -gyel, a háromszög másik két szögét a szokott módon -val és -val, akkor végül is a következő összefüggéshez jutottunk: | |
Azt kell belátnunk, hogy ez és közé esik. Osszuk el mindkét oldalt -vel, a jobb oldal második, harmadik és negyedik tagja esetében azt is a megfelelő két oldal és a közbezárt szög szinusza szorzataként írva, akkor a | |
arányról kell belátnunk, hogy és 5 közötti érték.
Felhasználva a könnyen igazolható azonosságot, a jobb oldal a következőképpen is írható:
Ebből az alsó becslés érvényessége nyilvánvaló, és az is látható, hogy az arány nem éri el a értéket, de ahhoz tetszés szerint közel lehet, ha az egyik szög csak kevéssel kisebb -nál, a másik kettő pedig ennek megfelelően nagyon kicsi.
Felső becsléshez alkalmazzuk 2 tagra a majd a | |
összefüggést:
mert . Fejezzük még ki -t -val, akkor a becsülendő kifejezés így alakítható tovább:
Ez a kifejezés nem nagyobb, mint 4. Egyenlő akkor lehet vele, ha , a kivonandó pedig 0. Mivel a szereplő szögek -nál kisebbek, ez azt jelenti, hogy tehát a háromszög szabályos.
Eredményeinket összefoglalva a bizonyítandó állításon kicsit túlmenően azt láttuk be, hogy a előjeles terület és között változik. Az alsó határt nem éri el, de ahhoz tetszés szerint közel lehet, a felső határt viszont eléri, éspedig egyedül a szabályos háromszög esetén.
Megjegyzés. A megoldás során alkalmazott területátalakítások közt szerepelt egy négyszög területének kétféle felosztása háromszögekre is. Ennek ‐ az négyszög esetén ‐ az felel meg, hogy (1) mindkét oldalához hozzáadjuk az területet. Ez a jobb oldal utolsó tagjával 0-t ad, így
 4. ábra
Megjegyezzük, hogy ezzel nemcsak konvex, hanem még hurkolt négyszöghöz is rendeltünk területet (4. ábra), vagyis olyanhoz, amelyiknek az oldalai metszik egymást a csúcsoktól különböző pontban is. Ez a hozzárendelt érték a csúcsok megnevezési sorrendjében történő körüljárás során pozitív irányban körüljárt rész területéből kivonva a negatív irányban körüljárt rész területét. A (2) összefüggés szerint ez esetben is mind a két lehetséges "felosztás'' háromszögekre ugyanarra a területértékre vezet.
II. megoldás. Használjuk továbbra is az első megoldás jelöléseit. Tükrözzük a háromszög csúcsait a szemközti oldalszakaszok felezőpontjára is, a tükörképek legyenek , , . Az , , egyenesek párhuzamosak rendre a háromszög , , oldalaival, így egy ahhoz hasonló háromszöget alkotnak. Ezt a háromszöget az eredetiből úgy kaphatjuk meg, hogy azt a súlypontjából négyszeresére nagyítjuk. Valóban, ez a nagyítás az oldalfelező pontokat az , , -be viszi át ‐ mivel a súlypont harmadolja a súlyvonalakat ‐ , a háromszög oldalegyeneseit pedig párhuzamos egyenesekbe (5. ábra).
 5. ábra
Az szakasz megkapható úgy, hogy a oldal felezőpontja és a magasság talppontja közti szakaszt -ból kétszeresére nagyítjuk. -ben viszont az oldalfelező pont és a magasságtalppont közti szakasz négyszer akkora, mint az eredeti háromszögben, tehát -ben az oldalfelező pont és a magasságtalppont közti szakasz felezőpontja.
Észrevételünket a következő egyszerű segédtétel ismételt alkalmazásával fogjuk hasznosítani: Legyen az háromszög síkjának tetszés szerinti pontja , és tükörképe -re . Ekkor Mérjük a egyenestől a távolságot előjelesen úgy, hogy az -t tartalmazó félsík pontjainak a távolsága legyen olyan előjelű, mint az körüljárási irány, a másik félsíkban levő pontoké pedig ellenkező előjelű. Ekkor a háromszögek területe úgy számítható, mint a távolság szorozva a hozzá tartozó magassággal, a magasságokra pedig érvényes a megfelelő összefüggés (6. ábra).
 6. ábra
Jelöljük -ben az , , -et tartalmazó oldalakon levő magasság talppontokat rendre , , -vel, a háromszög csúcsait pedig , , -mal. Ekkor, kétszer alkalmazva (3)-at
Itt , mert párhuzamos -vel, az utóbbi háromszög pedig az háromszög kétszeres nagyítása, területe tehát . A többi háromszöget (3) alapján tovább bontva | |
Itt az első és a harmadik tag ismét -vel egyenlő, mert és . Az utolsó tag a háromszög talpponti háromszögének területe, ez az eredeti háromszög talpponti háromszöge területének 16-szorosa. A maradó három háromszög egy-egy csúcsa oldalfelezőpont, így ezeket tovább alakíthatjuk (3) alapján: | |
A zárójel első és utolsó tagja, továbbá a maradó két-két szomszédos tagpár egy-egy négyszög területét adja. Ezeket (2) alapján a másik átlójukkal osztva ketté,
A bal oldalak összege a zárójel 6 tagját adja, a jobb oldalak első oszlopa és egyszer a talpponti háromszög pedig -t, aminek a területe . Kétszer talpponti háromszögéé , így végül a következő összefüggést kaptuk:
Az háromszöget pozitív körüljárás szerint betűztük meg, a talpponti háromszög körüljárási iránya azonban hegyesszögű háromszög esetén pozitív, tompaszögű háromszögnél viszont negatív.Azt kell tehát belátnunk, hogy értéke és közé esik.
Hegyesszögű háromszögnek legyen az -nál levő szöge a legnagyobb vagy a legnagyobbak egyike. A , , oldalakon levő magasságtalppont legyen rendre , , . A -en át -vel és -vel húzott párhuzamosak a paralelogrammát metszik ki a háromszögből (7. ábra). Ez tartalmazza a talpponti háromszöget. Ez azért igaz, mert és húrnégyszög, s így mindkettő -nél levő külső szöge a -gel egyenlő, a két párhuzamos tehát az egyiknek, ill. a másiknak a szögteréhez tartozik. Ekkor azonban az , az szakaszon van.
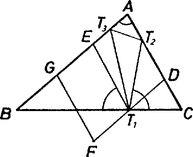 7. ábra
Legyen . Ekkor mérjük rá meghosszabbítására a vele egyenlő szakaszt. Az -en át -vel párhuzamosan húzott egyenes messe -t -ben. Az paralelogrammának a háromszögön túlnyúló része egybevágó a háromszöggel, így a paralelogramma területe nem nagyobb a háromszögénél. A paralelogramma és az általa tartalmazott talpponti háromszög területe tehát nem nagyobb, mint .
Ha az háromszögben -nál tompaszög van, akkor a talpponti háromszög sorrendben történő körüljárása ellenkező irányú, mint az háromszögé. (8. ábra).
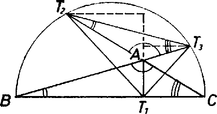 8. ábra
A terület abszolút értékét nézve a háromszög hasonló -hez és kisebb nála, mert az utóbbinak az egyik oldala a kör átmérője. Az , háromszögek területe kisebb a velük közös oldalú , ill. háromszögekénél, mert a közös oldalhoz tartozó magasságok az utóbbi háromszögekben nagyobbak. Ebben az esetben tehát a talpponti háromszög területe kisebb a háromszög területének kétszeresénél. Ezzel a feladat állítását bebizonyítottuk.
Megjegyzések. 1. Ez a megoldás is szolgáltatja az I. megoldásban nyert pontosabb eredményt. Egy paralelogrammába írt háromszög területe ugyanis nem nagyobb, mint a paralelogramma területének a fele, és akkora csak úgy lehet, ha a háromszög két csúcsa a paralelogramma két szomszédos csúcsa, a harmadik csúcs pedig az ezek közti oldallal szemközti oldalon van. Ebből következik, hogy hegyesszögű háromszög talpponti háromszögének a területe nem nagyobb a háromszög területének a negyedénél, és könnyen látható, hogy egyenlő egyedül a szabályos háromszög esetén lesz.
Tompaszögű háromszög esetében viszont látható a bizonyításból, hogy a talpponti háromszög területe közel lehet -hez, ha és közel van -hez, ill. -hez, de azt nem érheti el.
2. Megoldhatjuk a feladatot koordinátageometria segítségével is. Választhatjuk pl. a oldal egyenesét -tengelynek és az -ból rábocsátott merőlegest -tengelynek. Célszerű továbbá a -ből és -ből induló magasságok talppontjai koordinátáival fejezni ki és tükörképét. Ezúton eljuthatunk akár az I., akár a II. megoldásban nyert területformulához.
3. Azok számára, akik ismerik a vektorok vektoriális szorzatát, vázolunk egy ezt felhasználó megoldást. A és vektor vektoriális szorzatán, -n azt a vektort értjük a térben, amelyiknek hossza a vektorok meghatározta paralelogramma területe, iránya merőleges a két vektor síkjára és annak arra az oldalára mutat, amelyikről nézve pozitív irányban forgatható -nál kisebb szöggel -be. Ez a művelet nem kommutatív, hiszen a tényezők felcserélésével előjelet vált. Előjelet vált a szorzat akkor is, ha az egyik vektort az ellentettjével helyettesítjük. Ennek megfelelően, ha mindkét vektor előjelét megváltoztatjuk, vagy az egyik előjelét változtatjuk és a tényezőket megcseréljük, akkor a vektoriális szorzat értéke nem változik. Azt kell még tudni róla, hogy disztributív:
| |
Az háromszög kétszeres területét az szorzat adja. A tényezőket így határozhatjuk meg: | |
mert pl. (9. ábra).
 9. ábra
Hasonlóan , és így a kettőt tagonként összeszorozva -et a következő vektorok előjeles hosszának összege adja ‐ az -vel egy irányba mutató vektorok hosszát tekintve pozitívnak, az azzal ellentétes irányúakét negatívnak ‐ | |
Az első tag , az utolsó . A közbülső kettőben az oldalt a rajta levő talpponttal osztva a | |
összeg kétszeresét kapjuk. Az összeg egyes tagjai a , , , háromszögek kétszeres területét adják, ezeknek az összege pedig az háromszög területe (10. ábra). Ezeket figyelembe véve a formulához jutunk.
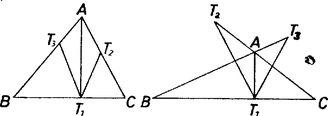 10. ábra
A koordinátákkal felírható területformula tagjait alkalmasan csoportosítva ugyanezeknek a háromszögeknek a területeit ismerhetjük fel.
4. Volt, aki az , , oldalak négyzetét fejezte ki az oldalakkal és a szögek háromszorosaival, és helyettesítette be a Heron‐formulába. Ezen az úton is el lehet jutni ‐ elég fáradságosan ‐ az I. megoldás formulájához.
Surányi János egyetemi tanár
Budapest, ELTE
Lásd pl. Erdős P.‐Surányi J.: Válogatott fejezetek a számelméletből,Tankönyvkiadó, Budapest,1960. 114‐122.old. (Itt 3 bizonyítás is található.)A derékszögű háromszögnél két magasságtalppont egybeesik a derékszögű csúcsban, így , tehát ezekre mindig , amit könnyű közvetlenül belátni.(Ez a tény vezetett egyébként a feladathoz.) |
 PDF | MathML
PDF | MathML