Cím: Milyen szabályos rács-sokszögek léteznek?
Szerző(k):  Bogdán Zoltán 
Füzet: 1986/december, 433 - 434. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A matematikának azt a területét, amelyben geometriai módszerekkel oldunk meg számelméleti problémákat, vagy fordítva, geometriai számelméletnek nevezzük. Ennek az elméletnek egyik legfontosabb eszköze a koordináta-rendszer, alapvető fogalma a négyzetrács (vagy általánosabban a paralelogrammarács). Rácspontnak nevezzük a sík minden olyan pontját, amelynek derékszögű koordinátái egész számok, a négyzetrács pedig a síkbeli rácspontok összessége. Rács-sokszögnek ezután olyan sokszöget nevezünk, amelynek minden csúcsa rácspont.

*

Vizsgáljuk meg először, van-e a síkon szabályos rácsháromszög. Tegyük fel, hogy az ABC háromszög ilyen, legyen ennek oldala a. Feltevésünk szerint a csúcsok koordinátái egész számok, így a2 ‐ Pitagorasz tételével kiszámítva ‐ ugyancsak egész. Foglaljuk a háromszöget az 1. ábra szerint egy, a koordináta-tengelyekkel párhuzamos oldalú támasztéglalapba. (Egy konvex tartomány támaszegyenesének nevezünk egy egyenest, ha annak van a tartománnyal közös pontja, és a tartomány minden pontja ‐ a közös pontok kivételével ‐ az egyenesnek ugyanarra az oldalára esik. A támasztéglalap mindegyik oldalegyenese támaszegyenes.)
 
 
1. ábra
 

Az 1. ábra alapján világos, hogy mind a téglalap, mind pedig a téglalapból a háromszög oldalai által levágott derékszögű háromszögek területe racionális szám, ezért a szabályos háromszög területe is az. Ez azonban azt jelentené, hogy az oldal felhasználásával kapott terület a234, szintén racionális. Ez viszont lehetetlen, mert mint láttuk, a2 egész, és így a234 irracionális szám. A kapott ellentmondás azt jelenti, hogy nem létezik szabályos rácsháromszög.
 
1. feladat. Létezik-e szabályos rácshatszög?
 
2. feladat. Van-e a térben olyan szabályos háromszög, amelynek mindegyik csúcsa rácspont?
*

Négyoldalú szabályos rács-sokszög, rácsnégyzet nyilván létezik. Mi a helyzet nagyobb oldalszám esetén? Megmutatjuk, hogy ha n=5 vagy n>6, akkor nincs a síkon olyan szabályos n-szög, amelynek csúcsai kivétel nélkül rácspontok.
Bizonyítás közben a négyzetrács alapvető tulajdonságai közül kettőt használunk:
 
1. Ha egy paralelogramma három csúcsa rácspont, akkor a negyedik is az.
 
2. A rácsnak egy korlátos síkidom belsejébe csak véges sok pontja eshet.
Tegyük fel, hogy állításunkkal ellentétben létezik ilyen S rácssokszög. A 2. ábrán A1,A2,...,An jelöli ennek csúcsait. Tükrözzük az A1-et az A2An átlóra. Ha a tükörkép B1, akkor az 1. tulajdonság alapján B1 is rácspont. A többi csúccsal hasonlóan járva el, a B1,B2,...,Bn rácspontokat kapjuk.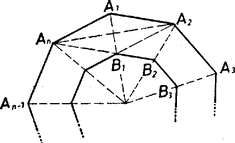
 
 
2. ábra
 

Könnyen igazolható, hogy az n=5, illetve n>6 esetekben a B1 pontok az S sokszög belsejének különböző pontjai.
 
3. feladat. Bizonyítsuk be a most kimondott állítást.
Ha most a kapott ábrát az S középpontja körül 360∘/n szöggel elforgatjuk, akkor nyilván önmagába megy át: a Bi rácspontok tehát ugyancsak egy n oldalú szabályos sokszög csúcsai. Az S rács-sokszög tehát a belsejében tartalmaz egy szabályos n oldalú rács-sokszöget.
A gondolatmenetet újra és újra megismételve tetszőlegesen sok rácsponthoz juthatunk az S belsejében, ami viszont nem lehetséges. Ezzel a bizonyítást befejeztük, az 1. feladat eredményével együtt pedig minden esetben választ adtunk a címben fölvetett kérdésre.
 
4. feladat. Keressünk olyan rácsnégyzetet, amelynek oldalai nem párhuzamosak a koordináta-tengelyekkel.
 
5. feladat. Bizonyítsuk be az 1. és 2. tulajdonságot a kockarácsban!
 
Érdeklődő olvasóink figyelmébe ajánljuk Reiman István A geometria és határterületei című kitűnő könyvének 14. fejezetét.