Kezdőlap


Cím:	Kvaterniók (Fordította Sapsál Anna)
Szerző(k):	Miscsenko, A. , Szolovjov, J.
Füzet:	1986/november, 337 - 344. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hogyan készíthetünk pontokból számokat?

Ha az egyenes pontjairól van szó, akkor ez nagyon egyszerű. Ha már kiválasztottuk a számolás kiindulási pontját (a ,,nullát'') és egy irányított szakaszt (az ,,egységet''), akkor az egyenesből számegyenest készíthetünk, és ezzel az egyenes minden pontjából egy valós számot kapunk, a pont koordinátáját (1. ábra).

1. ábra

A sík pontjainál bonyolultabb a helyzet. Ha megválasztottuk a kiindulási pontot (az origót) és két egymásra merőleges tengelyt, akkor a sík minden pontjához hozzárendelhetjük az

(x; y)

számpárt, a koordinátáit a síkon. Ahhoz, hogy ezek a számpárok, ,,dupletek'' számként viselkedjenek, meg kell tanulnunk ezeket a dupleteket ,,összeadni'' és ,,szorozni'', méghozzá úgy, hogy az összeadás és szorzás szokásos tulajdonságai megmaradjanak (kommutativitás, asszociativitás, disztributivitás, az inverz műveletek, a kivonás és osztás létezése).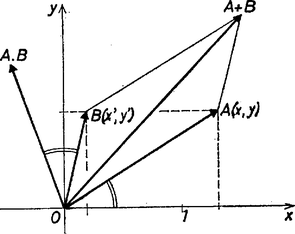

2. ábra

Az összeadás egyszerű. A dupleteket vektorokként természetes módon adhatjuk össze ‐ koordinátánként (2. ábra):

\begin{matrix} (x; y) + (x'; y') = (x + x'; y + y') . \end{matrix}

(1)

A szorzással már bonyolultabb a helyzet.^{$^{*}$} Egy nem túl bonyolult formula azonban itt is megadja a megoldást:

\begin{matrix} (x; y) \cdot (x'; y') = (x x' - y y'; x y' + x' y) . \end{matrix}

(2)

Nem nehéz ellenőrizni, hogy a dupletek ezen szorzása az (1) összeadással együtt kielégíti az előzőekben felsorolt szokásos tulajdonságokat. Ily módon a dupleteket az (1) és (2) műveletekkel teljes értékű számhalmaznak tekinthetjük.
Valójában a dupletek nem mások, mint a komplex számok. Általában nem

(x; y)

alakban írják fel őket, hanem

x + y i

formában, ahol

i

‐ a képzetes egység

(

(0; 1)

duplet

)

, amely a következő érdekes tulajdonsággal rendelkezik: (

i^{2} = i \cdot i = - 1

). Ez aztán lehetővé teszi a négyzetgyökvonást (a komplex számok körében) negatív számokból.
De hogyan készíthetnénk számokat a tér pontjaiból? Egy koordináta-rendszert bevezetve a pontokat itt is koordinátáikkal lehet megadni, de már nem kettővel, hanem hárommal: (

x; y; z

). Ezeket a számhármasokat, tripleteket természetes módon lehet koordinátánként összeadni:

\begin{matrix} (x; y; z) + (x'; y'; z') = (x + x'; y + y'; z + z') . \end{matrix}

(3)

A tripleteket majd akkor tekinthetjük számoknak, ha találunk egy módszert a szorzásra, amely a (3) összeadással együtt rendelkezik ennek a két műveletnek a szokásos tulajdonságaival. Többek között, hogy a szorzásnak létezik inverze (osztás a nemnulla elemekkel).
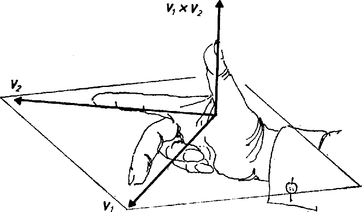
Hogyan lehet hát szorozni a tripleteket? Ez a feladat 1833-ban kezdte el foglalkoztatni Hamilton (1805‐1865) ír matematikust. De erről a rendkívüli emberről érdemes külön is szólni.

Hamilton

Hamilton sokoldalú és igen tehetséges ember volt. Tíz éves korában Homérosz sok versét tudta fejből, tizennégy évesen pedig már kilenc nyelvet beszélt. 1824-ben az Ír Királyi Akadémia lapjában jelentette meg a geometriai optikáról szóló munkáját, 1827-ben megkapta Írország királyi csillagászának címét.
1833-ban Hamilton a Dancing-i (Dublin mellett) obszervatórium igazgatójának posztját töltötte be, és sok optikai és analitikus mechanikai munka szerzőjeként volt ismert. A geometriai optika területén elért eredményeiből kiindulva megjósolta a kétszeres kúpszerű törés jelenségét a két tengelyű kristályokban, amelyre aztán kollégája, Lloyd, hamarosan példát is talált.
Egy hosszú évtizeden keresztül próbált Hamilton valamilyen ésszerű szorzást találni a tripletek körében ‐ sikertelenül. Később egy fiának írott levélben így emlékezett erre: ,,Minden reggel, amikor lejöttem a reggelihez, te és az öcséd, William Edvin, általában megkérdeztétek: Nos, apa, tudsz már tripleteket szorozni? Amire kénytelen voltam mindig bánatosan azt válaszolni: Nem, csak összeadni és kivonni tudom őket.''

Vektorszorzás

A feladat, aminek a megoldásával Hamilton kísérletezett, eleinte egyszerűnek tűnt. Az, hogy hogyan kell összeadni a vektorokat, világos

(a (3) formula alapján

), már csak a szorzás képletét kell megtalálni, valamilyen, a dupletek szorzásánál használt (2)-höz hasonló formulát. De mindazok a képletek, amelyeket Hamilton végigpróbált, vagy az egyik, vagy a másik tulajdonságnak nem tettek eleget. Már akkor is jól ismert volt a vektoriális szorzás művelete: a

v_{1}

és

v_{2}

nem nulla vektorok

v_{3} = v_{1} \times v_{2}

vektoriális szorzata az a vektor, amely merőleges a

v_{1}

és a

v_{2}

vektorok síkjára, irányát a jobbkéz-szabály határozza meg (3. ábra), hossza pedig

| v_{1} | \cdot | v_{2} | \cdot sin (v_{1}, v_{2}

). A továbbiakhoz megjegyezzük, hogy ha a

v_{1}

és

v_{2}

vektorokat koordinátáikkal adjuk meg a derékszögű koordináta-rendszerben:

\begin{matrix} v_{1} = (α_{1}; β_{1}; γ_{1}), \\ v_{2} = (α_{2}; β_{2}; γ_{2}), \end{matrix}

akkor

\begin{matrix} v_{1} \times v_{2} = (β_{1} γ_{2} - β_{2} γ_{1}; γ_{1} α_{2} - γ_{2} α_{1}; α_{1} β_{2} - α_{2} β_{1}) . \end{matrix}

(4)

3. ábra

De a vektoriális szorzás művelete nem volt alkalmas Hamilton számára, mivel nincs inverze. Például ha

v_{1} = v_{2} \neq 0

, akkor a (

v_{1}, v_{2}

) szög 0. Ez azt jelenti, hogy szorzatuk,

v_{3} = v_{1} \times v_{2}

egyenlő lesz

0

-val. Ha minden nem

0

vektorral lehetne osztani, akkor

(v_{1} \times v_{2}) : v_{2} = v_{1} \neq 0

lenne akkor, amikor

v_{1} \times v_{2} = 0

, és így

(v_{1} \times v_{2}) : v_{2} = 0

. A kapott ellentmondás jól mutatja, hogy a

v_{2}

-vel való osztás lehetetlen.
Csak tisztelettel és csodálattal adózhatunk annak a ténynek, hogy a sikertelenség és csalódások ellenére Hamilton nem adta fel a reményt, és tíz évig irigylésre méltó kitartással próbálta megoldani az önmaga számára kitűzött feladatot. Bár a feladatot nem sikerült megoldani (és nem is lehetett ‐ hogy miért, arról majd később szólunk), a tíz éves munka nem veszett kárba. Egy szép napon, 1843-ban, Hamilton egyszer csak úgy döntött, hogy ne a tripleteken (számhármasokon), hanem a számnégyeseken, vagy ahogyan azonnal elkeresztelte őket, a kvaterniókon kellene definiálni a szorzást. Így történt a dolog:

A Brog-i hídon történt

Hamilton így emlékezett az egyik, fiához írott levélben, amelyet a kor szokásos kissé dagályos stílusában vetett papírra: ,,Október 16-odik napja volt, egy hétfői nap, az Ír Királyi Akadémia Tanácsa ülésének napja, ahol nekem kellett elnökölnöm. Anyáddal együtt indultam oda a Királyi csatorna mentén: bár beszélt hozzám valamit, egyáltalán nem fogtam fel, amit mond, mert a tudatomban valami derengeni kezdett. Váratlanul mintha zárult volna egy áramkör: fellobbant egy szikra, amely bevilágította sok hosszú év egy irányba fordított gondolatait, az én ‐ vagy ha úgy alakul, akkor mások munkáját, ha még elegendő tudatos élet adatik meg nekem, hogy tájékoztassam a világot felfedezésemről. Nem tudtam leküzdeni magamban azt a vágyat, hogy késsel a híd puha kövébe véssem az

i

j

k

szimbólumok közötti alapvető összefüggéseket:

\begin{matrix} i^{2} = j^{2} = k^{2} = ijk = - 1, \end{matrix}

amely megoldotta a problémát, persze a felirat régen lekopott. De sokkal tartósabb feljegyzés maradt erről a napról az Akadémiai Tanács Feljegyzések Könyvében, ahol feljegyezték, hogy engedélyt kértem és kaptam arra, hogy a szakosztály első ülésén előadást tartsak a kvaterniókról. Az előadást meg is tartottam a következő hónap november 13-adik napján, hétfőn''.

A kvaterniók meghatározása

A kvaterniók ‐ valós (

x; y; u; v)

számnégyesek, amelyeket a következő formában írhatunk fel kényelmesen:

\begin{matrix} q = x + y i + u j + v k, \end{matrix}

ahol i, j és k ‐ új számok, a komplex számok képzetes egységének felelnek meg. Az i, j, k számoknak a következő összefüggéseket kell kielégíteniük:

\begin{matrix} i^{2} = j^{2} = k^{2} = - 1, & (5) \\ ij = - ji = k, jk = - kj = i, ki = - ik = j . & (6) \end{matrix}

Ezeket az összefüggéseket ,,szorzótábla'' formájában kényelmes felírni (4. ábra).

\begin{matrix} \times & i & j & k \\ i & - 1 & k & - j \\ j & - k & - 1 & i \\ k & j & - i & - 1 \end{matrix}

4. ábra

Az összeadás és a szorzás meghatározása a szokásos szabályok alapján a zárójelek felbontásával és az (5)‐(6) szabályok alapján az egyforma tagok összevonásával történik.
A definíciónak megfelelően ha

q_{1}

és

q_{2}

két kvaternió, akkor

\begin{matrix} q_{1} & + q_{2} = (x_{1} + y_{1} i + u_{1} j + v_{1} k) + (x_{2} + y_{2} i + u_{2} j + v_{2} k) = & (7) \\ = x_{1} + y_{1} i + u_{1} j + v_{1} k + x_{2} + y_{2} i + u_{2} j + v_{2} k = \\ = (x_{1} + x_{2}) + (y_{1} i + y_{2} i) + (u_{1} j + u_{2} j) + (v_{1} k + v_{2} k) = \\ = (x_{1} + x_{2}) + (y_{1} + y_{2}) i + (u_{1} + u_{2}) j + (v_{1} + v_{2}) k . \end{matrix}

Ez persze nyilvánvalóan a megszokott ,,koordinátánkénti'' összeadás. A kvaterniók szorzata a következőképpen számolható ki :

\begin{matrix} q_{1} q_{2} = (x_{1} + y_{1} i + u_{1} j + v_{1} k) (x_{1} + y_{2} i + u_{2} j + v_{2} k) = & (8) \\ = (x_{1} x_{2} - y_{1} y_{2} - u_{1} u_{2} - v_{1} v_{2}) + (x_{1} y_{2} + y_{1} x_{2} + u_{1} v_{2} - v_{1} u_{2}) i + \\ + (x_{1} u_{2} + u_{1} x_{2} - y_{1} v_{2} + v_{1} y_{2}) j + (x_{1} v_{2} + v_{1} x_{2} + y_{1} u_{2} - u_{1} y_{2}) k . \end{matrix}

Egy hosszadalmas, de teljesen gépiesen elvégezhető ellenőrzés mutatja, hogy a kvaterniók szorzása asszociatív, azaz

\begin{matrix} (q_{1} q_{2}) q_{3} = q_{1} (q_{2} q_{3}) . \end{matrix}

Természetesen a valós és a komplex számok felfoghatók a kvaterniók speciális eseteként. Így például a valós

x

szám ‐ a következő alakú kvaternió:

\begin{matrix} x = x + 0 \cdot i + 0 \cdot j + 0 \cdot k . \end{matrix}

(9)

Az az olvasó, aki nem ismeri a komplex számokat, ne jöjjön zavarba: tekintse a (9) formulát a (7)-es és (8)-as formulákkal együtt a komplex számok definíciójának. Hasznos lesz, ha felírja a (8)-as formulát a (9)-es esetre, és összehasonlítja azt a (2)-es formulával (a szorzás definíciója).
A kvaterniók összeadásánál nyilvánvalóan létezik a megfordítás ‐ a kivonás. Mégpedig két kvaternió, a

q_{1}

és a

q_{2}

különbsége a következő formulával határozható meg:

\begin{matrix} q_{1} - q_{2} = (x_{1} - x_{2}) + (y_{1} - y_{2}) i + (u_{1} - u_{2}) j + (v_{1} - v_{2}) k . \end{matrix}

q_{1} = q_{2}

, akkor a

q_{1} - q_{2}

különbség a zérus kvaternió, ugyanis

\begin{matrix} q_{1} - q_{2} = 0 + 0 \cdot i + 0 \cdot j + 0 \cdot k = 0. \end{matrix}

A kvaterniók osztása

Térjünk most át a kvaterniók osztására, amely a szorzás inverz művelete. Gondoljuk meg, hogyan értelmeztük az

a

szám

b

-vel való osztásának hányadosát? (

b \neq 0

.) Ez egy olyan

c

szám, amelyre

\begin{matrix} b c = a . \end{matrix}

(10)

Így értelmeztük az osztást a valós és a komplex számok körében. Sajnos, a kvaterniókra ez a meghatározás közvetlenül nem alkalmazható. A következőképpen áll a dolog. Ahhoz, hogy a (10)-es formula ,,korrektül'' határozza meg a hányadost, az szükséges, hogy a szorzat ne függjön a tényezők sorrendjétől.
Ellenkező esetben a

c = b^{- 1} a

hányados mellett, amelyet a (10)-es formula határoz meg, létezik egy teljesen egyenrangú

c'

hányados, amelyet a

\begin{matrix} c' b = a \end{matrix}

formula határoz meg, és amely különbözhet a (10) által meghatározott

c

hányadostól. Itt kellett Hamiltonnak még egy áldozatot hoznia azon kívül, hogy ki kellett lépnie a három dimenziós térből.
Kiderült, hogy az általa meghatározott új számok, a kvaterniók elvesztettek még egy megszokott tulajdonságot: a kvaterniók szorzata függ a tényezők sorrendjétől. Valóban, már a (6)-os formulában is előjelet vált a szorzat, ha a tényezők sorrendjét felcseréljük.
Ily módon csak ,,bal oldali osztásról'' és ,,jobb oldali osztásról'' beszélhetünk. Nézzük meg, hogyan lehet például megkeresni a

q_{1}

kvaternió

q_{2}

-vel történő ,,bal oldali'' osztásának hányadosát? (

q_{2} \neq 0

.)
Jelölje a keresett hányadost

q = x + y i + u j + v k

. A kvaterniók szorzásának összefüggéseit és a bal oldali hányados definícióját felhasználva a következő egyenlőséget kapjuk:

\begin{matrix} q q_{2} = q_{1}, \end{matrix}

azaz

\begin{matrix} (x x_{2} - y y_{2} + u u_{2} - v v_{2}) + (x y_{2} + y x_{2} + u v_{2} - v u_{2}) i + \\ + (x u_{2} + u x_{2} - y v_{2} - v y_{2}) j + (x v_{2} + v x_{2} + y u_{2} - u y_{2}) k = \\ = x_{1} + y_{1} i + u_{1} j + v_{1} k . \end{matrix}

A kapott egyenlőség egyenértékű a következő

x

y

u

v

változójú lineáris egyenletrendszerrel:

\begin{matrix} x_{2} x - y_{2} y - u_{2} u - v_{2} v & = x_{1} \\ y_{2} x + x_{2} y + v_{2} u - u_{2} v & = y_{1} \\ u_{2} x - v_{2} y + x_{2} u - y_{2} v & = u_{1} \\ v_{2} x + u_{2} y - y_{2} u + x_{2} v & = v_{1} . \end{matrix}

Gyakorlásként javasoljuk, hogy az olvasó oldja meg ezt az egyenletrendszert és ezzel határozza meg

q_{1}

-nek

q_{2}

-vel való bal oldali osztásának hányadosát. Hasonló módon kereshető meg a

q_{1}

-nek

q_{2}

-vel való jobb oldali osztásának hányadosa is.
Tekintsük most azt a speciális esetet, amikor a

q_{1}

osztandó egyenlő az 1 valós számmal. Ebben az esetben akár jobbról, akár balról osztjuk a

q_{1} = 1

számot

q_{2}

-vel, ugyanazt a hányadost kapjuk, mint azt az olvasó is beláthatja:

\begin{matrix} p = \frac{x_{2} - y_{2} i - u_{2} j - v_{2} k}{x_{2}^{2} + y_{2}^{2} + u_{2}^{2} + v_{2}^{2}} . \end{matrix}

Ezt a

q

kvaterniót a következőképpen jelöljük:

\begin{matrix} q^{- 1} = \frac{x_{2} - y_{2} i - u_{2} j - v_{2} k}{x_{2}^{2} + y_{2}^{2} + u_{2}^{2} + v_{2}^{2}} . \end{matrix}

Ezután ha a

q_{1}

kvaterniót elosztjuk

q_{2}

-vel, akkor a ,,jobb oldali hányados'' a következő formulával fejezhető ki:

\begin{matrix} q_{j} = q_{2}^{- 1} q_{1}, \end{matrix}

a ,,bal oldali hányados'' pedig a következő formulával:

\begin{matrix} q_{b} = q_{1} q_{2}^{- 1} . \end{matrix}

A gyakorlatban két kvaternió hányadosát más módszerrel szokták meghatározni. Ehhez a következő dologra lesz szükségünk.

Skaláris és vektoriális kvaterniók

Ugyanúgy, ahogy a komplex számok is felírhatóak valós és képzetes részük összegeként, a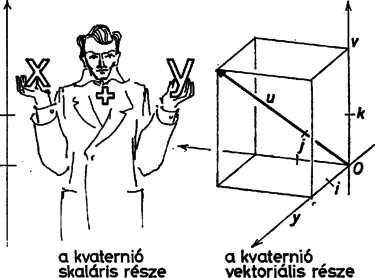

\begin{matrix} q = x + y i + u j + v k \end{matrix}

kvaternió is felírható a következő összegként:

\begin{matrix} q = x + (y i + u j + v k) . \end{matrix}

Ebben a felbontásban az első tagot a kvaternió skaláris részének nevezzük, a második tagot pedig vektoriális résznek. Az

x

skaláris rész egyszerűen csak egy valós szám, míg az

y i + u j + v k

vektoriális rész egy vektorral ábrázolható a három dimenziós térben:

\begin{matrix} r = y i + u j + v k, \end{matrix}

ahol az i, j és k egy derékszögű koordináta-rendszer egységvektorai (5. ábra).

5. ábra

Ily módon minden kvaternió felírható egy

x

valós szám és egy r vektor összegeként:

\begin{matrix} q = x + r . \end{matrix}

r = 0

, akkor

q = x

, és a

q

kvaterniót skaláris kvaterniónak nevezzük. Ha pedig

x = 0

, akkor

q = r

, és

q

-t vektoriális kvaterniónak nevezzük.
Összeadásnál a kvaterniók skaláris és vektoriális részei egymástól függetlenül adódnak össze.
A kvaterniók szorzásánál bonyolultabb a helyzet. Ha

q_{1}

és

q_{2}

skaláris kvaterniók, akkor

q_{1} q_{2}

szorzatuk szintén skaláris kvaternió. Abban az esetben, ha

q_{1} = x

skaláris,

q_{2} = r

pedig vektoriális kvaternió, akkor a szorzatuk,

q_{1} q_{2} = x (y i + u j + v k) = (x y) i + (x u) j + (x v) k

vektoriális kvaternió, a szorzás pedig nem más, mint az r vektor szorzása az

x

valós számmal.
Végül, ha mindkét kvaternió vektoriális:

\begin{matrix} q_{1} = r_{1} = y_{1} i + u_{1} j + v_{1} k, \\ q_{2} = r_{2} = y_{2} i + u_{2} j + v_{2} k, \end{matrix}

akkor

\begin{matrix} q_{1} q_{2} & = - (y_{1} y_{2} + u_{1} u_{2} + v_{1} v_{2}) + (u_{1} v_{2} - v_{1} u_{2}) i + \\ + (v_{1} y_{2} - y_{1} v_{2}) j + (y_{1} u_{2} - u_{1} y_{2}) k . \end{matrix}

Amint az jól látható a legutolsó formulából, a

q_{1} q_{2}

szorzat skaláris része egyenlő az (

r_{1}, r_{2}

) skaláris szorzat ellentettjével. A

q_{1} q_{2}

vektoriális része viszont régi ismerősünk, az

r_{1} \times r_{2}

vektoriális szorzat felírása koordináták szerint

(lásd (4)

).
Összefoglalva az összes áttekintett esetet, általános formulát kapunk a kvaterniók szorzására. Ha

q_{1} = x_{1} + r_{1}

q_{2} = x_{2} + r_{2}

, akkor

\begin{matrix} q_{1} q_{2} = (x_{1} \cdot x_{2} - r_{1} \cdot r_{2}) + (x_{1} \cdot r_{2} + x_{2} \cdot r_{1} + r_{1} \times r_{2}) . \end{matrix}

No és mi van a tripletekkel?

Vajon miért nem sikerült Hamiltonnak megfelelő módszert találnia a tripletek szorzására? Nem a találékonysága vagy a munkaszeretete hiányzott ‐ korábban utaltunk már arra, hogy a mondott értelemben a feladat megoldhatatlan. Valóban, bebizonyították, hogy lehetetlen olyan szorzást találni a háromdimenziós számokon, amelyre teljesülnének az általunk meghatározott tulajdonságok (asszociatív, disztributív a koordinátánkénti összeadásra nézve, és lehet osztani a nem nulla elemekkel). Sőt, ismert az összes olyan eset, amikor ilyen szorzás bevezethető. Amint azt Frobenius (1849‐1917) német matematikus bebizonyította, ez három esetben lehetséges: egy dimenzióban (a közönséges valós számok), két dimenzióban (a komplex számok) és ,,négy dimenzióban'' (a kvaterniók).

Mi történt a későbbiekben?

Hamilton és követői nagy reményeket fűztek a kvaterniókhoz. Ugyanolyan eredményeket vártak tőlük, mint a komplex számoktól, sőt még többet, és valóban, a kvaterniókkal történő számolás segítségével gyönyörű matematikai formulákra bukkantak, amelyek egy sor fontos fizikai jelenséget írnak le. De a további remények a kvaterniók algebrai és analízisbeli fejlődéséről nem váltak be.
A kvaterniók körében például nem teljesül az algebra alaptétele, amely szerint kvaternió-együtthatós polinomoknak léteznének gyökei a kvaterniók körében, sőt van olyan egyváltozós kvaternióegyütthatós polinom, amelynek minden kvaternió gyöke.
Az optimizmust kételkedés váltotta fel. Századunk elején a matematikusok felhagytak a kvaterniók iránti érdeklődéssel. De az idő múlt, a fizikusok pedig kitartóan kerestek olyan matematikai formalizmust, amellyel leírható néhány, az elemi részecskék spinjével kapcsolatos jelenség. Mikor felismerték a szerepüket bizonyos geometriai transzformációs terek felépítésében, amelyeket a kvantumfizikában használtak, a kvaterniókat újból elismerték.

A kvaterniók geometriai tulajdonságainak vizsgálata ‐ különösen nagy téma. Erről talán más alkalommal szólunk.
A KVANT-ból fordította:
Sapsál Anna

^{$^{*}$}A koordinátánkénti

(x; y) (x; y) = (x \cdot x; y \cdot y)

szorzás nem vezet semmi jóra; az így értelmezett műveletnek nincs inverze. (Például a (0; 2) dublettel nem lehet osztani.)