|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A szelídítő belép az oroszlán ketrecébe. Azonnal látja, hogy a vadállat morcos kedvében van. Az ajtó azonban becsapódott és belülről nem is nyitható, ráadásul senki sincs hallótávolságban. A szelídítő tudja, hogy ő és az oroszlán egyformán gyorsak. Természetesen kíváncsi, vajon
a) van-e olyan stratégiája, amellyel tetszőleges ideig el tud menekülni, függetlenül attól, hogy a bestia mit tesz; vagy
b) létezik-e a (végtelen intelligenciájúnak feltételezett) oroszlán számára olyan stratégia, amelyet követve képes megfogni őt, bármit is tesz ellene?
‐ Ha a ketrec az egész sík lenne ‐ töpreng az ember bánatosan ‐, akkor az oroszlán kezdeti helyétől egy egyenes mentén egyre távolodva futnék, és biztos megmenekülnék. De sajnos ott van a rács. Így azután nagyon úgy néz ki, hogy a szelídítőből az állatok királyának tápláléka lesz.
Célunk, hogy felvidítsuk szegényt, és ezért bizonyítjuk, hogy meg tud menekülni (1. tétel). Sőt ha a támadás a Szahara közepén történt volna, még egy pálmafát is ültethetne, és ezt követően tudna úgy mozogni, hogy mindig a fa árnyékában marad, függetlenül ennek méretétől, útja konvergál egy , ponthoz, és a bestia mindvégig éhen marad. Szinte szükségtelen hozzátenni, hogy emberünk titokban fogja tartani az pont helyét. Ez már csak azért is könnyen fog menni, mert maga sem tudja, hol lesz ez a pont; ennek helye ugyanis függ az oroszlán mozgásától.
1. Tétel. Adott pozitív mellett van a szelídítőnek olyan stratégiája, amelyet követve meg tud menekülni az oroszlán elől és e közben soha nem kerül indulási pontjától egységnél távolabbra.
2. Tétel. Adott pozitív mellett van a szelídítőnek olyan stratégiája, amelyet követve soha nem kerül a kiindulási helyétől r egységnél messzebbre, útja konvergál egy ponthoz, amit nem feltétlenül ér el, de eközben az oroszlán nem tudja elfogni.
Az 1. tétel A. S. Besicovitch-tól származik. Az eredeti bizonyítás alapötletét fogjuk használni, de a mi bizonyításunk talán könnyebben követhető.
Az 1. tétel bizonyítása
Jelölje a és pontok távolságát. Legyen és az oroszlán és a szelídítő kezdeti helyzete. Feltehetjük, hogy . Legyen adott.
1. A szelídítő választ egy tetszőleges pontot a ketrec belsejében úgy, hogy az egész szakasz is a ketrecen belül legyen és teljesülnek a következők:
| |
Mivel a ketrec belsejében van, létezik olyan pozitív szám, hogy és az középpontú, sugarú körlemez teljes egészében a ketrec belsejében fekszik. A szelídítő a tőle telhető legnagyobb sebességgel egy egyenes vonal mentén átfut -ból -be. De előbb még átgondolja, hogy útja során az oroszlán nem tudja elkapni, hiszen -val és -sel jelölve az oroszlán és a szelídítő helyét egy adott pillanatban, az 1. ábra szerint | |
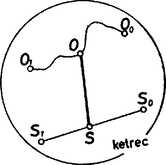 1. ábra
Amíg az ember -ból -be rohan, az oroszlán valamilyen vonalon eljut -ból mondjuk -be. Mielőtt a szelídítő -ből továbbindulna, sürgősen bebizonyítja az alábbi 1. lemmát.
1. Lemma. | |
Bizonyítás: Mivel | |
minden -re, az végtelen sorban van végtelen sok diszjunkt, egymás utáni számokból álló blokk, melyek összege legalább . Így világos, hogy a sor divergens.
Másrészt ha akkor
Miután a szelídítő bizonyította a lemmát, egy darab krétával, amit az oroszlán volt szíves odadobni neki, gondosan megjelöli a ketrec padlóján az pontot.
2. Tegyük fel, hogy emberünk épségben (anélkül, hogy az oroszlán elfogyasztotta volna) elérte az pontokat valamilyen természetes számra. Jelölje azt a pontot, ahol az oroszlán tartózkodik, amikor a szelídítő -ben van. Emberünk sietve bebizonyítja a 2. lemmát:
2. Lemma. Ha a szelídítő maximális sebességgel fut -ből az szakaszra merőleges egyenes mentén, az oroszlán nem tudja utolérni.
Bizonyítás: Legyen az oroszlán, illetve a szelídítő helyzete (2. ábra).
 2. ábra
Ekkor | |
Az oroszlánszelídítő és a matematikai pontosság szempontjából egyaránt életbevágó, hogy az utolsó egyenlőtlenség és nem .
A lemma bizonyítása után a szelídítő maximális sebességgel szalad az egyenesen távolságra, úgy választva meg az irányt, hogy ha csak az előzőleg megjelölt pont nincs rajta véletlenül az egyenesen, futás közben eleinte közeledjen hozzá. (3. ábra).
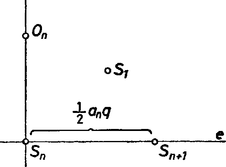 3. ábra
(Pillanatnyilag még fél attól, hogy futás közben nekimegy a ketrecnek és összetöri magát, amivel az oroszlán szabad prédájává válik. A 3. lemma szerencsére eloszlatja ebbéli aggályát.)
Ha ezt a szabályt követi, a 2. lemma szerint az oroszlán nem tudja elkapni. Útjának hossza összesen
| |
ami az 1. lemma szerint végtelen. És mivel véges, a leírt mozgás a végtelenségig tart. Már csak azt kell megmutatnunk, hogy az pont valóban a ketrec belsejében van. Ez következik abból, ha megmutatjuk, hogy
3. Lemma. | |
Bizonyítás: Jelölje az pontnak az egyenestől vett távolságát, és az merőleges vetületét az egyenesen.
1. eset (4. ábra). Ekkor | |
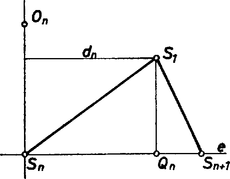 4. ábra
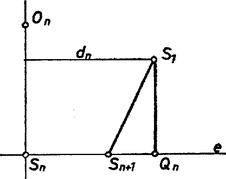 5. ábra
2. eset. (5. ábra). Ekkor | |
Ezzel a 3. lemmát be is bizonyítottuk.
A lemmában helyébe értékeket helyettesítve adjuk össze a kapott egyenlőtlenségeket: | |
és így . Ezek szerint választása miatt az egész út a ketrec belsejében fekszik. Tehát valóban megmentettük az oroszlánszelídítőt. Végül vegyük észre, hogy | |
A 2. tétel bizonyítása
Egy alkalmasan választott délibáb segítségével a szelídítő könnyedén elképzelheti, hogy az oroszlánnal együtt egy ketrecben vannak, és így különböző és értékekre alkalmazhatja az 1. tételt. Legyen a szelídítő kiindulási pontja és legyen az 1. tételben , . Használjuk a már leírt stratégiát egészen addig, amíg az ember által megtett út hossza el nem éri az -et, ahol egy tetszőleges, de rögzített természetes szám. Jelölje azt a pontot, ahová így eljutott. Most változtassuk meg a stratégiát az , értékeknek megfelelően. Ezt ismét csak addig kövessük, amíg az ebben a fázisban megtett út hossza az pontnál eléri az -et. Most megint megváltoztatjuk az eljárást az , választásnak megfelelően, és emellett is kitartunk egy újabb hosszú út erejéig stb.
Az így menekülő embert az oroszlán az egyes részfutamokban az 1. tétel szerint nem éri utol, az út összhossza összesen , vagyis a szelídítő örök időkre megmenekül.
Állítsuk meg emberünket -ból felé futtában egy pontban azért, hogy megvizsgálhassuk helyzetét. Hogy ez ne okozzon gondot a menekülésben, tekintsük e művelet idejét nullának. Vegyük észre, hogy | |
és így állandóan élvezheti a pálmafa árnyékát, feltéve, hogy elég kicsi,
Még azt kell bizonyítani, hogy a szelídítő pályája konvergens. Minden utáni fázisban, mikor emberünk mondjuk és között egy pontban van,
ami tetszőlegesen kicsi, ha elég nagy. Felhasználva Cauchy konvergencia kritériumát, következik, hogy az út konvergál egy ponthoz. Magát a kritériumot ezen a szinten nehéz volna pontosan megfogalmazni, mert lényegesen túlhaladná ennek a kis jegyzetnek a kereteit.
Tanulság: Ha egy oroszlánnal kerülnél szembe, semmi ok az aggodalomra, feltéve hogy akármilyen kicsire össze tudod húzni magad, és akármilyen nagy gyorsulást el tudsz viselni.
Itt, elvben, még egy lehetőség van: akár a szelídítő, akár az oroszlán választ stratégiát, a másik tud nyerni a stratégia ellen. Bár szinte magától értetődő, hogy ez esetünkben nem lehetséges, ennek szigorú bizonyítása lényegesen meghaladná lapunk kereteit. ‐ Szerk. |
 PDF | MathML
PDF | MathML