Cím: A lámpácskás játékról
Szerző(k):  Mérő László 
Füzet: 1986/április, 145 - 150. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A múlt havi számunkban kitűzött feladatok egyikében a következő játék szerepelt: Egy ötször ötös négyzetrács minden pontjában van egy lámpácska, amely nyomógombként is működik. Ha valamelyik gombot megnyomjuk, akkor az ebben levő lámpa, valamint mindazok, amelyek a megnyomott gombbal oldal mentén szomszédosak, állapotot váltanak, tehát amelyik korábban égett, az a nyomás hatására elalszik, amelyik pedig korábban nem égett, az kigyullad. Kezdetben egyetlen lámpa sem világít. Elérhetjük-e, hogy valamennyi lámpa világítson, illetve, hogy csak a bal alsó sarokban levő lámpa égjen?
Ez a játék számos érdekes matematikai problémát vet fel. Ebben a cikkben ezek egy részével foglalkozunk.
Először is vegyük észre, hogy egy adott lámpa a játék végén akkor és csakis akkor fog világítani, ha a játék során páratlan sok szomszédját nyomtuk meg, önmagát is beleértve. Ebből látszik, hogy ha egy gombot a játék során kétszer is megnyomunk, akkor a végeredményen nem változtat, ha mindkét nyomást elhagyjuk. Eszerint feltehető, hogy minden gombot legfeljebb egyszer nyomunk meg. Észrevételünkből látszik, hogy a lenyomások sorrendje sem befolyásolja a végeredményt. Így tehát minden próbálkozás lényegében egyértelműen leírható úgy, hogy az egyes gombokról megmondjuk, hogy megnyomjuk-e őket vagy sem.
Ezek alapján bevezethetjük a következő jelöléseket. Jelöljük a gombokat (és egyben a lámpákat is) a1,a2,...,a25-tel az 1. ábra szerint. Egy X lenyomásmintát ezután az x1,x2...,x25 számokkal írunk le, ahol xi=1 akkor, ha az ai gombot megnyomjuk, és 0 akkor, ha nem. Minden X lenyomásminta egyértelműen meghatároz egy Y világításmintát, amit hasonlóan írhatunk le az y1,y2,...,y25 számokkal, azaz yi=1, ha az X lenyomásminta lenyomása után az ai lámpa ég, és 0, ha nem.

 
 
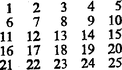1. ábra
 

Valamennyi lámpa kigyújtása olyan X lenyomásminta meghatározását jelenti, amelynek megfelelő világításmintában minden i-re yi=1. Vegyük észre, hogy ha egy lenyomásminta első sorát (tehát az x1, x2, x3, x4, x5 számokat) tetszőlegesen lerögzítjük, akkor a lenyomásminta második sorának elemeit már csak egyféleképpen választhatjuk meg úgy, hogy a világításminta első sorában minden lámpa égjen. Ezután már a lenyomásminta harmadik sora is csak egyféle lehet, ha azt akarjuk, hogy a világításminta második sorában is égjenek a lámpák. Továbbmenve, a lenyomásminta negyedik, majd ötödik sora is hasonlóképpen egyértelmű, és ezután már több szabadságunk nincs: az adott (x1,...,x5) kezdet csak egyféleképpen folytatható úgy, hogy a kapott lenyomásmintához tartozó világításmintában az első négy sor minden lámpája égjen, és ezzel az is egyértelműen van meghatározva, hogy az ötödik sorban mely lámpák égnek és melyek nem.
Ha tehát a fenti kitöltést valamennyi lehetséges (x1,...,x5) szám ötösre elvégezzük, akkor megkapjuk az összes olyan lenyomásmintát, amikor a megfelelő világításmintában az első négy sor összes lámpája ég. Ilyen kezdő számötös 25=32 van (mivel minden xi egymástól függetlenül lehet 0 vagy 1). E 32 kezdősor végigpróbálása után négy olyan lenyomásmintát kapunk, aminek megfelelő világításmintában az utolsó sor lámpái is égnek. Ezek (2. ábra) tehát a kitűzött feladat b) részének összes megoldásai. (Az ábrán látható, hogy a megoldások egymás elforgatottjai.)
 
 
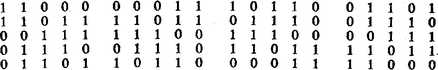2. ábra
 

Ha már az ember kezében vannak a lámpácskák, kíváncsi rá, hogy elkészíthető-e tetszőleges világításminta. Abból, hogy négy különböző lenyomásminta is ugyanazt a (csupa 1-esből álló) világításmintát adja, azonnal következik, hogy van olyan világításminta, amelyet egyetlen lenyomásminta sem hoz létre, hiszen az összes világításminták száma ugyanannyi, mint az összes lenyomásminták száma: 225. Azonban ennél többet is mondhatunk.
 

Nevezzük két lenyomásminta összegének azt a lenyomásmintát, amit a két minta egymás utáni végrehajtásaként kapunk a bevezetőben említett egyszerűsítés figyelembevételével. Az összegben tehát akkor kell megnyomnunk egy gombot, ha ezt a gombot az összeadandó minták közül pontosan az egyikben nyomjuk meg. A lenyomásmintákat jellemző 0‐1 sorozatok nyelvén ez éppen az elemenként vett, modulo 2 összeadást jelenti. Az is látszik, hogy lenyomásminták összege a megfelelő világításminták összegét gyújtja ki.
Ha most páronként összeadjuk a 2. ábra lenyomásmintáit, akkor olyan lenyomásmintákat kapunk eredményül, amelyek hatására egyetlen lámpa sem világít.
Nevezzük az ilyen lenyomásmintákat 0-lenyomásmintáknak. A 2. ábra négy mintája között (42)=6-féle összeadás végezhető el, de az összegek közül csak három különböző. Ezek a 0-lenyomásminták láthatók a 3. ábrán. Ha ehhez a három mintához még hozzávesszük a triviális 0-lenyomásmintát is (amikor egyetlen gombot sem nyomunk le), akkor egyelőre 4 különböző 0-lenyomásmintánk van. Megmutatjuk, hogy több 0-lenyomásminta nincs.
 
 
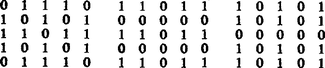3. ábra
 

Ha egy X mintához hozzáadunk egy 0-lenyomásmintát, akkor az eredményként kapott lenyomásmintához tartozó világításminta ugyanaz lesz, mint az X-hez tartozó. Ha tehát lenne még egy ötödik 0-lenyomásminta is, akkor azt hozzáadva a 2. ábra (pl.) első megoldásához, szintén megoldást kellene kapnunk. Azt viszont már tudjuk, hogy a feladat összes megoldása a 2. ábrán látható, így tehát az összeadás eredményeként a 2. ábra valamelyik másik mintáját kell megkapnunk. Mivel a minták összeadása asszociatív, és tetszőleges X és X' mintára (X+X')+X'=X, a 2. ábra két szóban forgó mintájának összege az új, ötödik 0 benyomásminta. Az ilyen összeadások eredményei azonban a 3. ábrán láthatók, ötödik 0-lenyomásminta tehát valóban nem létezik.
Az eddigiekből következik, hogy ha egy világításminta előállítható, akkor az pontosan négyféleképpen állítható elő: úgy, hogy az őt előállító bármely lenyomásmintához hozzáadjuk a 0-lenyomásmintákat. Eszerint a 225-féle világításmintának legfeljebb az 1/4-e lehet kigyújtható. A valóban kigyújtható minták száma azonban nem lehet ennél kevesebb sem, mert egyébként volna olyan minta, amelyet a 225 darab lenyomásminta közül négynél több állítana elő.
Nyitva maradt persze a kérdés, hogy miképpen lehetne valahogy egyszerűen jellemezni 223 darab valóban előállítható mintát. Ezzel kapcsolatos a kitűzött feladat a) része.
A kérdés vizsgálatához próbáljuk meg a játékot a "negyedére korlátozni'', azaz tekintsük azt a játékot, amely csak az a1,a2,...,a23 lámpákból áll, és nézzük meg, hogy ennek megoldásai hogyan hatnak a24-re és a25-re. Az eredeti feladat megoldásához hasonlóan megmutatható, hogy a 23-lámpás játékban csak a triviális 0-lenyomásminta létezik, és így minden világításminta valóban létre is hozható.*
A 23-lámpás játékban tehát minden ai gombhoz van olyan lenyomásminta (méghozzá egyetlen), amelyik csak az ai lámpát gyújtja ki. Most vizsgáljuk meg, hogy ezek a 23-gombos lenyomásminták hogyan hatnak az eredeti játék a24 és a25 lámpáira. A 4. ábrán látható például az a lenyomásminta, ami a 23-lámpás játékon csak az a1-et gyújtja ki. Látható, hogy a 25-lámpás játékon ez a minta nem gyújtja ki a24-et, de kigyújtja a25-öt. * (Az ábrán aláhúzással jelöltük a kigyújtott lámpákat.)
 
 
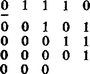4. ábra
 

Készítsük el ezután a következő táblázatot. a25 helyére írjunk 1-est, a24 helyére pedig 2-est. A többi ai helyére írjunk 0-t, ha a 23-lámpás játékban az egyedül ai-t kigyújtó lenyomásminta a 25-lámpás játékban a24 és a25 egyikét sem gyújtja ki; 1-et, ha csak a25-öt gyújtja ki; 2-t, ha csak a24-et, és 3-at, ha mindkettőt kigyújtja. Az így kapott táblázat az 5. ábrán látható, és valamiképpen a 23-lámpás játék hatását írja le az elhagyott két lámpán.
 
 
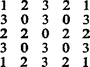5. ábra
 

Most vizsgáljuk meg, hogy a 25-lámpás játékban egy gomb lenyomása hogyan változtatja meg a 0, 1, 2, ill. 3-mal jelölt mezők közül azoknak a paritását, amelyek éppen világítanak. A táblázat szimmetriái miatt elég az 1, 2, 3, 6, 7, 8, 11, 12, 13 számú gombokat vizsgálni. A 3. és 11. gomb egyik szám paritását sem változtatja meg, ezt jelöljük így: (0, 0, 0, 0). Az 1. gomb nem változtatja meg a 0-k paritását, de a többiekét igen, ezt jelöljük így: (0, 1, 1, 1). A 2. és 6. gombok hatása: (1, 1, 1, 1), a többieké pedig: (1, 0, 0, 0). Vegyük észre, hogy valamennyi gomb hatása (a, b, b, b) alakú!
Ez azt jelenti, hogy az üres mintából kiindulva csak azok a világításminták lehetnek kigyújthatók, amelyekben a táblázatban 1-es, 2-es, ill. 3-as helyeken levő égő lámpák száma azonos paritású, hiszen az üres mintában is ez a helyzet. Az ilyen minták viszont ki is gyújthatók, hisz "23-lámpás részüket'' a 23-as játékban egyesével kigyújtva, az 5 táblázat kódjainak jelentése szerint a24 és a25 állapota éppen megfelelő. Ez valóban az összes minták negyedrésze, mivel ha az első 23 lámpára tetszőlegesen megadjuk, hogy égjen-e vagy sem, azzal a világító 3-asok paritását már meghatároztuk. Ezután a 24. és 25. lámpát összesen négyféleképpen állíthatjuk még be, de ebből egyetlenegy beállítás lesz olyan, amikor a világító 1-esek és a 2-esek paritása megegyezik a 3-asok (már adott) paritásával. Az 5. ábra táblázata tehát mintegy "kulcsként'' használható annak gyors eldöntésére, hogy egy világításminta létrehozható-e vagy sem. A kitűzött feladat a) részére így tagadó a válasz, hiszen az egyetlen világító lámpa a21, így a világító 1-esek paritása 1, a többieké pedig 0. Az is látszik, hogy az önmagukban kigyújtható lámpák a 0-jelűek, a7, a9, a13, a17 és a19.
Amikor az ember valódi játékot tervez a lámpácskák ötletéből, igyekszik minél többféle játéklehetőséggel felruházni a készítendő fizikai eszközt. Az egyik bővítési lehetőség az, ha a játékosnak különböző, " véletlen'' kezdőalakzatokból kiindulva kell ‐ minél kevesebb lépésben ‐ meggyújtania valamennyi lámpát. Természetesen valamennyi kezdőalakzatról biztosítani kell a megoldhatóságot. Az 5. ábra táblázata lehetőséget ad ilyen alakzatok gyors generálására.
A feladatot mégsem így oldottuk meg, mert ahhoz, hogy annak idején a játék olcsón gyártható legyen, minél kisebb mikroprocesszort kellett alkalmazni; végül az összes funkció belefért egy 1K-s négybites chip-be. A "véletlen'' kezdőállásokat úgy hoztuk létre, hogy kiválasztottunk egy adott kezdőállást és 16 lépést: amikor a játékos a véletlen kezdőállást kéri, a gép ezt a 16 lépést hajtja végre (ötösével ciklikusan). A játékba így csak 32 "véletlen'' kezdőállás van beépítve ‐ ez gyakorlati szempontból elég, és a program is belefért az 1K-ba. Az adott kezdőállást és a 16 lépést viszont sikerült úgy megválasztanunk, hogy egyik "véletlen'' kezdőállást sem lehet 6-nál kevesebb lépésben megoldani.
Egy játék értékét az is növeli, ha többféleképpen is játszhatunk vele. Például módosítjuk a szomszédságokat: egy gomb lenyomása nem a tényleges szomszédok állapotát változtatja meg. A következő tétel garantálja, hogy a játéknak igen általános feltételek mellett is van megoldása, azaz valamennyi lámpa kigyújtható. A valódi játékba mi egy olyan lehetőséget is bevettünk, hogy az egyes gombok lenyomása után azok a lámpák váltsanak állapotot, ahova az adott gombon álló sakkhuszár el tudna ugrani. Ennek a változatnak az elemzését az olvasóra hagyjuk és visszatérünk az általános játék vizsgálatára.
*

Játsszuk a játékot az a1,...,an gombok An halmazán, és tegyük fel, hogy minden ai gombhoz hozzá van rendelve egy Ui halmaz úgy, hogy az ai gombot lenyomva az Ui halmaz elemei váltanak állapotot. Az Ui halmazokról a következőket tesszük fel:
a) Minden i-re ai∈Ui.
b) Minden i, j párra, ha ai∈Uj, akkor aj∈Ui.
Ez a két feltétel az eredeti játékra ‐ és a lóugrásos változatra is ‐ nyilván teljesül. Most bebizonyítjuk a következő tételt:
Tétel. A fenti játéknak mindig van megoldása, azaz létezik An-nek olyan H részhalmaza, hogy H elemeit megnyomva minden ai lámpa állapotot vált.
Bizonyítás. A bizonyítást n-re vonatkozó teljes indukcióval végezzük. n=1-re a tétel nyilvánvalóan igaz. Tegyük fel, hogy a tétel igaz n-1 lámpa esetére, és tekintsük az n lámpás játékot az An gombokon.
Ha n páros, akkor minden ai lámpa esetére vizsgáljuk meg azt az n-1 lámpás játékot, amelyet az An-{ai} gombokkal játszunk úgy, hogy minden U halmazból elhagyjuk ai-t, az U halmazok közül pedig Ui-t. Erre a játékra is nyilván teljesülnek az a) és b) feltételek, így az indukciós feltevés szerint ennek a játéknak van megoldása. Ha a megoldó lenyomásmintát végrehajtjuk An-en, és az ott kigyújtja az ai lámpát is, akkor készen vagyunk. Ha egyetlen ai-re sem gyújtja ki ai-t, akkor egymás után hajtsuk végre az összes (n-1)-lámpás játék megoldásaként kapott lenyomásmintát az An halmazon. Ennek során minden lámpa (n-1)-szer, azaz páratlan sokszor vált állapotot, tehát a kapott n darab lenyomásminta összege megoldása az n-lámpás játéknak.
Ha n páratlan, akkor először is belátjuk, hogy létezik olyan Ui halmaz, amelynek az elemszáma páratlan. Ez következik abból, hogy a ∑i=1n|Ui| összeg páratlan, ami azért igaz, mert ebben az összegben az a) feltétel miatt minden ai lámpát egyszer magában Ui-ben számolunk (ez tehát egy páratlan összeg), a továbbiakban pedig ha egy ai lámpát számolunk egy Uj-ben, akkor a b) feltétel szerint az ai lámpát is számoljuk Ui-ben, tehát a további leszámolások párba állíthatók.
Vegyünk most egy olyan ai gombot, amihez páratlan elemszámú Ui tartozik. Most csak ennek az Ui halmaznak az elemeire végezzük el azt a gondolatmenetet, amit páros esetben az An minden elemére elvégeztünk. Ha egyetlen (n-1)-lámpás megoldás sem gyújtja ki az elhagyott lámpát, akkor a kapott |Ui| számú lenyomásmintát egymás után végrehajtva az An halmaz minden Ui-n kívüli eleme páratlan sokszor vált állapotot, az Ui halmaz elemei pedig eggyel kevesebbszer, azaz páros sokszor. Ha ezután még az ai gombot is lenyomjuk, akkor Ui elemei még egyszer állapotot váltanak, így ebben az esetben is megoldáshoz jutottunk. Ezzel a tételt bebizonyítottuk.
Ha az a) vagy a b) feltételt elhagyjuk, akkor már mutatható ellenpélda, azaz olyan játék, amelynek nincs megoldása. A b) feltételt elhagyva nagyon egyszerű ellenpélda a következő: három gombunk van, a, b és c. Az a lámpa kigyújtja önmagát és b-t; a b lámpa kigyújtja önmagát és c-t; a c lámpa pedig önmagát és a-t. Könnyen látható, hogy ennek a játéknak nincs megoldása.
Az a) feltétel elhagyása esetén ellenpélda az eredeti ötször ötös játék azzal a módosítással, hogy a lenyomott gomb csak a szomszédait gyújtja ki, önmagát nem. Közvetlenül is aránylag könnyen bebizonyítható, hogy ez a játék nem oldható meg, de például az alábbi 3. feladatból is következik: a mostani játék egy megoldása az eredeti játékban egy komplementer‐kigyújtó lenne.
*

A továbbiakban még néhány érdekes feladatot sorolunk fel a lámpácskás játékkal kapcsolatban, majd egy-két eddig megoldatlan problémát is megemlítünk.
1. Bizonyítsuk be, hogy az eredeti, 5×5-ös játékban minden létrehozható világításminta legfeljebb 15 lenyomással is előállítható.
2. Bizonyítsuk be, hogy az eredeti játék n-szer n-es négyzetre általánosított változatában mindig létezik pontosan 2n olyan lenyomásminta, ami megegyezik az általa létrehozott világításmintával.
3. Bizonyítsuk be, hogy az n-szer n-es játékban páros n esetén pontosan 2n olyan lenyomásminta van, amely saját komplementerét gyújtja ki; páratlan n esetén pedig nem létezik ilyen komplementer-kigyújtó.
4. Bizonyítsuk be, hogy az n-szer n-es játékok között létezik végtelen sok olyan, amiben minden világításminta létrehozható, és végtelen sok olyan is van, amelyikben nem.
Ez utolsó feladattal kapcsolatos első megoldatlan problémánk is: hogyan lehetne jellemezni azokat az n-eket, amelyekre az n-szer n-es játékban minden világításminta létrehozható. Számítógéppel 100-ig meghatároztuk az ilyen n-eket, ezek a következők:
1236781012131518202122252627283136373840424345464851525556575860636668707273757678808182858687889091939697100

Látható, hogy ez a sorozat meglehetősen szeszélyesen viselkedik. Mi lehet benne a szabályszerűség?
Ugyancsak nem sikerült eddig általánosítani az 1. feladat eredményét n-szer n-es játékra. (Amikor minden világításminta létrehozható, akkor természetesen n2 a megoldás: az a világításminta, amit az összes gomb lenyomásával kapunk, ilyenkor nem hozható ki kevesebb lépésből.)
*Bonyolultabb, lineáris algebrai eszközökkel közvetlenül, általánosan is igazolható, hogy a kigyújtható minták száma pontosan az összes minták száma, osztva a 0-lenyomásminták számával.

*Természetesen a 23-lámpás feladat megoldását célszerű számítógéppel számolni.