Kezdőlap


Cím:	Az 1985. évi (16.) Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Szép Jenő
Füzet:	1985/november, 402 - 410. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elméleti feladatok

1. Egy fiatal rádióamatőr rádióösszeköttetést tart fenn két lánnyal, akik két különböző városban laknak. Két függőleges botantennát úgy helyez el, hogy amikor az

A

városban lakó lány a maximális jelet fogja, akkor a

B

városbeli lány semmilyen jelet nem vesz és megfordítva. Az antennarendszer két függőleges, azonos teljesítményű botantennából áll, amelyek a vízszintes síkban minden irányban egyformán sugároznak.
a) Határozd meg az antennarendszer paramétereit, vagyis a botantennák közötti távolságot, az antennák elhelyezkedését és a kibocsátott elektromos jeleik közötti fáziskülönbséget úgy, hogy az antennák közötti távolság a lehető legkisebb legyen!
b) Add meg az eredményt numerikusan, ha a fiú a rádióadóját

27

MHz-en működteti és az antennarendszert Portorožban állítja fel! A térképen az

A

város (Koper) irányát az északhoz képest

72^{\circ}

-nak találta, a

B

város (egy istriai kisváros: Buje) és az északi irány közti szöget pedig

157^{\circ}

-nak mérte.

Megoldás. a) Az 1. ábra felülnézetben mutatja az

f

és

g

antennát. A két antennából az

A

város irányába sugárzott jelek útkülönbsége

Δ s_{A} = r cos (α + ψ)

. Hasonlóan a

B

város irányában sugárzott jelek útkülönbsége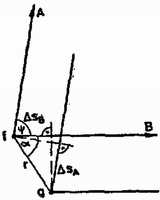

Δ s_{B} = r cos α

1. ábra

A

városba érkező jelek fáziskülönbsége

\begin{matrix} φ_{A} = (2 π / λ) Δ s_{A} + φ_{0} = (2 π / λ) r cos (α + ψ) + φ_{0}, \end{matrix}

(1)

ahol

φ_{0}

f

antenna fáziskésése a

g

antennához, képest

(0 ≦ φ_{0} < 2 π)

.
Hasonlóképpen

\begin{matrix} φ_{B} = (2 π / λ) r cos α + φ_{0} . \end{matrix}

(2)

Ha a rádióamatőr az

A

városban levő lánnyal beszélget, akkor a feladat feltétele szerint

\begin{matrix} φ_{A} = 2 k π és φ_{B} = (2 n + 1) π, \end{matrix}

(3)

ahol

k

és

n

egész számok. (1), (2) és (3) alapján

\begin{matrix} r = \frac{2 (k - n) - 1}{2 [cos (α + ψ) - cos α]} λ . \end{matrix}

(4)

r

távolságot kell minimalizálnunk. A számláló abszolút értéke akkor minimális, ha

k = n

vagy

k = n + 1.

Ahhoz, hogy a nevező abszolút értékének maximumát megtaláljuk, előbb alakítsuk át:

\begin{matrix} | 2 [cos (α + ψ) - cos α] | = | - 4 sin (α + \frac{ψ}{2}) sin \frac{ψ}{2} | . \end{matrix}

ψ

állandó, ezért a kifejezés akkor lesz maximális, ha

α + \frac{ψ}{2} = \frac{3 π}{2}

, vagy

α + \frac{ψ}{2} = \frac{π}{2}

. Az ábrának megfelelő megoldás az utóbbi, így

α = \frac{π}{2} - \frac{ψ}{2}

. Ez azt jelenti, hogy a két antenna által meghatározott egyenes merőleges a két város közti szög felezőjére.
Az eddigiek alapján a két antenna minimális távolsága

\begin{matrix} r_{min} = \frac{λ}{4 sin (ψ / 2) .} \end{matrix}

(1) és (3) segítségével a két antenna jelének fáziskülönbségére

2 k π + π / 2

-t kapunk, tehát

φ_{0} = π / 2

. Ha a

φ_{0}

fáziskülönbséget

π / 2

-ről

3 π / 2

-re változtatjuk, akkor mindkét városba érkező jelek fáziskülönbsége

π

-vel változik. Ekkor a rádióamatőr a

B

városban levő lánnyal tud beszélgetni, és az

A

városban levő lány nem hallja.
b) A megadott adatokkal

α = 47, 53^{\circ}

r_{min} = 4, 1

m. Az elrendezés a 2. ábrán látható.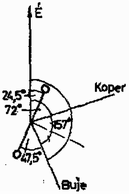

2. ábra

2. Egy

a

b

c

oldalélű

(a ≫ b ≫ c)

téglatest alakú rúd InSb félvezető anyagból készült. A rúdban

I

áram folyik a téglatest ,,

a

'' élével párhuzamos irányban. A rúd a ,,

c

'' éllel párhuzamos irányú,

B

indukciójú külső mágneses térben van. Az

I

áram által keltett mágneses tér elhanyagolható. Az áramot elektronok szállítják. Ha csak elektromos tér van jelen, akkor egy félvezetőben az elektronok átlagsebessége

v = μ E

, ahol

μ

az elektronok ,,mozgékonysága''. Ha mágneses tér is jelen van, akkor a teljes elektromos tér iránya már nem párhuzamos az elektromos áram irányával. Ezt a jelenséget Hall-effektusnak nevezik.
a) Határozd meg a rúdban a teljes elektromos tér nagyságát és irányát, amikor a rúdban a fent leírt áram folyik!
b) Határozd meg a rúd ,,

b

'' élére merőlegesen elhelyezkedő kél oldalának egy-egy szemközti pontja között a feszültségkülönbséget!
c) Fejezd ki a

b)

pontbeli feszültségkülönbség egyenfeszültség részét, ha az áramerősség és a mágneses indukció a következőképp változik:

I = I_{0} sin ω t

;

B = B_{0} sin (ω t + φ)

!
d) Tervezz olyan elektromos áramkört, amely a

c)

pontban kapott eredményt felhasználva méri egy váltóáramú elektromos készülék teljesítményfelvételét! Magyarázd meg a tervezett áramkör működését!
Adatok:
Az InSb-ben egy elektron ,,mozgékonysága'':

μ = 7, 8 m^{2} / Vs

.
Az elektronsűrűség az InSb-ben:

2, 5 \cdot 10^{22} m^{- 3}

\begin{matrix} I = 1, 0 A; B = 0, 10 T; b = 1, 0 cm; c = 1, 0 mm; e = 1, 6 \cdot 10^{- 19} As . \end{matrix}

Megoldás. a) Először számítsuk ki az elektronok sebességét a félvezetőben, valamint a mozgásukat létrehozó

E_{0}

elektromos tér nagyságát!

Δ t

idő alatt az

a

élre merőleges oldallapon

e n b c v Δ t

töltés halad át, ahol

n

az elektronok sűrűsége és

v

a sebessége. Az áramerősség tehát

I = e n b c v

. Innen

\begin{matrix} v = \frac{I}{e n b c} = 25 m/s . \end{matrix}

(1)

A feladat szövegéből tudjuk, hogy

v = μ E_{0}

. Így

\begin{matrix} E_{0} = \frac{V}{μ} = \frac{I}{e n b c μ} = 3, 2 V/m . \end{matrix}

(2)

A félvezetőben mozgó elektronokra, sebességükre merőlegesen, azaz a

b

él irányában hat a Lorentz-erő. Ennek hatására a

b

élre merőleges két oldallap annyira töltődik fel, hogy a feltöltődés által létrehozott elektromos tér

(E_{1})

a félvezetőben semlegesítse a Lorentz-erő hatását. (A jelenség valamelyest hasonlít ahhoz, mint amikor egy vezetőt külső elektromos térbe helyezünk.)
Az eddigiek alapján

E_{1} e = e v B

. (1) felhasználásával

\begin{matrix} E_{1} = \frac{B I}{e n b c} = 2, 5 V/m. \end{matrix}

(3)

Az eredő elektromos tér nagysága

E = \sqrt[]{E_{0}^{2} + E_{1}^{2}} = 4, 06

V/m, a tér iránya az

a

éllel

φ = arc tg E_{1} / E_{0} = 38^{\circ}

-os szöget zár be (3. ábra).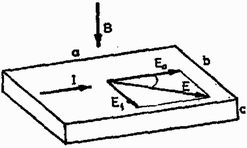

3. ábra

b) A keresett feszültség a két pont között

\begin{matrix} U = E_{1} b = B I / e n c = 25 mV . \end{matrix}

(4)

c) (4)-et felhasználva

\begin{matrix} U (t) = \frac{B_{0} I_{0}}{e n c} sin ω t \cdot sin (ω t + φ) . \end{matrix}

Egy trigonometriai átalakítás segítségével ezt a következő alakra hozhatjuk:

\begin{matrix} U (t) = \frac{B_{0} I_{0}}{e n c} sin^{2} ω t \cdot cos φ - \frac{B_{0} I_{0}}{e n c} sin 2 ω t \cdot sin φ . \end{matrix}

Látható, hogy a második tag egy

2 ω

körfrekvenciájú szinuszos váltakozó feszültség, amelynek nincs egyenfeszültség komponense.
Az első tag egy

sin^{2} ω t

szerint változó feszültség. Mivel

sin^{2} ω t

átlagos értéke

1 / 2

, ezért az átlagos egyenfeszültség

\begin{matrix} U_{e} = \frac{B_{0} I_{0} cos φ}{2 e n c} . \end{matrix}

(5)

d) A keresett áramkör egy lehetséges megvalósítása a 4. ábrán látható.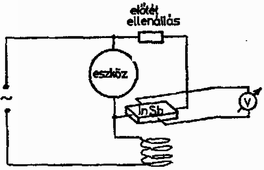

4. ábra

Tudjuk, hogy az eszköz hatásos teljesítménye

\begin{matrix} P = U_{e f f} I_{e f f} cos φ . \end{matrix}

(6)

A kapcsolásban a félvezetőn átfolyó áram minden pillanatban arányos az eszközre eső feszültséggel. Az előtétellenállást úgy kell megválasztani, hogy a félvezető árama sokkal kisebb legyen, mint az eszközön átfolyó áram. Ekkor a tekercs által létrehozott mágneses tér minden pillanatban arányos az eszközön átfolyó árammal.
(5) és (6) összevetésével láthatjuk, hogy a voltmérő által mutatott egyenfeszültség arányos lesz az eszköz hatásos teljesítményével. Ha tehát megfelelően kalibráljuk a voltmérőt, akkor azt az eszköz teljesítményének mérésére használhatjuk.

3. Egy űrkutatási programban két kilövési tervet dolgoztak ki arra, hogy egy űrszonda elhagyja a Naprendszert. Az első terv (I) az, hogy rögtön a Naprendszer elhagyásához elegendő sebességgel lövik fel. A második (II) terv szerint az űrszonda megközelít egy távolabbi bolygót, és ennek segítségével úgy változik meg a sebessége, hogy elérje a Naprendszer elhagyásához szükséges sebességet. Feltesszük, hogy a szonda vagy csak a Nap, vagy pedig csak a bolygó gravitációs tere hatására mozog ‐ attól függően, hogy melyik gravitációs tér erősebb az adott pontban.
a) Határozd meg annak a minimális

v_{a}

sebességnek a nagyságát és irányát a Földhöz képest, amellyel az űrszondát az első terv szerint ki kellene lőni!
b) Tegyük fel, hogy az űrszondát az a) pontban meghatározott irányban, de valamilyen más, a Földhöz képest

v_{b}

nagyságú sebességgel lőtték fel. Határozd meg az űrszonda sebességét, amikor a Mars pályáját keresztezi ‐ azaz számítsd ki ekkor a sebességének a Mars pályájával párhuzamos és rá merőleges komponensét! Amikor a szonda keresztezi a Mars pályáját, a Mars nincs a metszéspont közelében.
c) Most tegyük fel, hogy az űrszonda ,,belép'' a Mars gravitációs terébe. Legalább mekkora sebességgel kellett indítani a Földről a szondát, hogy az ezek után elhagyja a Naprendszert?
Útmutatás: Az a) pont eredménye alapján tudod, hogy optimális esetben milyen nagyságú és irányú sebességgel kell rendelkezzen az űrszonda, hogy miután elhagyta a Mars gravitációs terét, már elszakadjon a Naprendszertől. (Ne foglalkozz azzal, hogy a találkozás során pontosan hol van a Mars!) Mi a kapcsolat ezen szökési sebesség és a Mars gravitációs terébe érkezés előtti (a b) pontban kiszámított) sebességkomponensek között? Mi a helyzet az űrszonda energiájának megmaradásával?
d) Az energiának legfeljebb hányadrésze takarítható meg az (II) terv alkalmazásával az (I) tervbeli energiához viszonyítva?
Megjegyzések: Tegyük fel, hogy valamennyi bolygó ugyanabban az irányban és ugyanabban a síkban körpályán kering a Nap körül.
Hanyagold el a légellenállást, a Föld tengely körüli forgását, valamint a Föld gravitációs teréből való kilépésre fordított energiát!
Adatok: A Föld keringési sebessége a Nap körül

30 km/s

. A Föld és a Mars Naptól mért távolságának aránya

2 / 3

Megoldás. a) A Naprendszer elhagyásának feltétele az, hogy a szonda teljes

E

energiája nemnegatív legyen. A kilövés után közvetlenül:

\begin{matrix} E = \frac{m v^{2}}{2} - f \frac{m M}{r_{F}}, \end{matrix}

(1)

ahol

m

a szonda tömege,

v

a Naphoz viszonyított sebessége,

M

a Nap tömege,

r_{F}

a földpálya sugara és

f

a gravitációs állandó.
A Föld keringése során a Földre ható gravitációs erő a centripetális erő:

\begin{matrix} \frac{m_{F} v_{F}^{2}}{r_{F}} = f \frac{m_{F} M}{r_{F}^{2}}, \end{matrix}

(2)

ahol

m_{F}

és

v_{F}

a Föld tömege és sebessége. (2)-ből

\begin{matrix} v_{F}^{2} = f \frac{M}{r_{F}} . \end{matrix}

(3)

(1) és (3) felhasználásával a lehető legkisebb kilövés utáni sebesség

v = \sqrt[]{2} v_{F}

. A szonda Földhöz viszonyított sebessége a kilövés után

\begin{matrix} \vec{v_{a}} = \vec{v} - \vec{v_{F}} . \end{matrix}

\vec{v_{a}}

nagysága nyilván akkor a legkisebb, ha

\vec{v_{a}}

és

\vec{v_{F}}

egyirányú, tehát a szondát a Föld mozgásának irányába lőjük ki. Ekkor

\begin{matrix} v_{a} = (\sqrt[]{2} - 1) v_{F} = 12, 4 km/s . \end{matrix}

(4)

b) Jelöljük a szonda

v_{b} + v_{F}

nagyságú kezdősebességét

v_{0}

lal, továbbá használjuk az 5. ábra jelöléseit!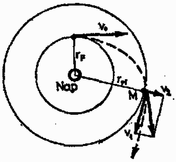

5. ábra

Írjuk fel a szonda mozgására a perdület megmaradását:

\begin{matrix} m v_{0} r_{F} = m v_{1} r_{M}, \end{matrix}

(5)

ahol

r_{M}

a marspálya sugara.
Az energia megmaradása

\begin{matrix} m \frac{v_{0}^{2}}{2} - f \frac{m M}{r_{F}} = m \frac{v_{1}^{2} + v_{2}^{2}}{2} - f \frac{m M}{r_{M}} . \end{matrix}

(6)

Bevezetve a

λ = r_{F} / r_{M}

jelölést, az (5) és (6) egyenletekből:

\begin{matrix} v_{1} = λ v_{0}, \end{matrix}

(7)

\begin{matrix} v_{2} = \sqrt[]{v_{0}^{2} (1 - λ^{2}) - 2 (1 - λ) v_{F}^{2}} . \end{matrix}

(8)

c) Az a térrész, ahol a Mars gravitációs tere erősebb, mint a Napé, nagyon kis méretű a marspálya méreteihez képest. Azt mondhatjuk tehát, hogy amikor a szonda a Mars pályájának keresztezése előtt belép a Mars gravitációs terébe, akkor a b) pontban kiszámított sebességgel rendelkezik.
Ekkor a szondának a Marshoz viszonyított relatív sebessége:

\begin{matrix} v_{r} = \sqrt[]{v_{2}^{2} + {(v_{1} - v_{M})}^{2},} \end{matrix}

(9)

ahol

v_{M}

a Mars keringési sebessége.
A Marshoz rögzített koordináta-rendszerből nézve a szonda a Mars gravitációs terében hiperbola pályán mozog.
Amikor a szonda elhagyja a Mars gravitációs terét, akkor a Marshoz viszonyított sebessége ugyanakkora, mint amikor oda belépett.
A szonda további mozgása olyan lesz, mintha a Marsról lőtték volna ki

v_{r}

nagyságú sebességgel. Alkalmazhatjuk tehát az a) rész eredményeit. Ideális esetben a Marsot elhagyva a szonda sebessége egyirányú a Mars sebességével, és a Naprendszer elhagyásának feltétele:

\begin{matrix} v_{r} = (\sqrt[]{2} - 1) v_{M} . \end{matrix}

(10)

A Mars sebességére a (3) egyenlethez hasonlót írhatunk fel:

\begin{matrix} v_{M}^{2} = f M / r_{M} . \end{matrix}

(11)

A (7)‐(11) egyenletekből

v_{0}

-ra egy másodfokú egyenletet kapunk, amelynek megoldása

\begin{matrix} v_{0_{12}} = v_{F} [λ^{3 / 2} \pm \sqrt[]{λ^{3} - 2 + 2 \sqrt[]{2} λ}] . \end{matrix}

Átalakítva:

\begin{matrix} v_{b_{12}} = v_{F} [{(\frac{r_{F}}{r_{M}})}^{3 / 2} - 1 \pm \sqrt[]{{(\frac{r_{F}}{r_{M}})}^{2} + 2 - 2 \sqrt[]{2} \frac{r_{F}}{r_{M}}} .] \end{matrix}

Az adatokat behelyettesítve, az egyik gyök negatív, a másik pedig

v_{b} = 5, 5

km/s.
Tehát a Mars gravitációs terének kihasználásával elegendő, ha a szondát csak

5, 5

km/s nagyságú sebességgel indítjuk el.
d) Az energiamegtakarítás

\begin{matrix} \frac{v_{a}^{2} - v_{b}^{2}}{v_{a}^{2}} = 80 % . \end{matrix}

Mérési feladatok

1. Vizsgáld meg a kis váltóáramú motor által hajtott sárgaréz korong gyorsulását és lassulását is! A félfordulatok mért idejéből ábrázold a korong szögelfordulását, a szögsebességét és a szöggyorsulását az idő függvényében! Határozd meg a motor forgatónyomatékát és teljesítményét a szögsebesség függvényében!

Berendezések:

‐ váltóáramú motor kapcsolóval és egy sárgaréz korong;

‐ indukciós érzékelő;

‐ sokcsatornás időmérő berendezés.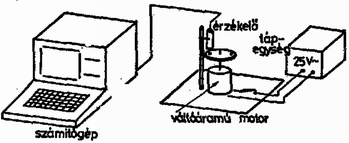

6. ábra

Útmutatás: Amikor a koronghoz erősített két vasbütyök valamelyike

0, 5 mm

-nél közelebb kerül az indukciós érzékelőhöz, az érzékeli ezt és egy jelet küld az időmérő berendezésnek.
A stopper egy számítógépbe van programozva úgy, hogy regisztrálja és a memóriában tárolja azt az időpillanatot, amelynél az érzékelő érzékeli a hozzá közeledő bütyköt. A stoppert egyszerűen az alábbi számok benyomásával működtetheted:

5 ‐ mérés. Maga a mérés nem azonnal kezdődik. A stopper akkor indul, ha beütöd annak a kódjelét, hogy hány mérést kívánsz végezni, azaz hányszor érzékelje a gép a bütyköket.

3 ‐ 30 mérés elvégzése.

6 ‐ 60 mérés elvégzése.
E két parancs bármelyikére elkezdődik a mérés. A mérés elvégzése után a képernyőn grafikus formában megjelenik az eredmény. A függőleges tengely a bütykök észlelése között eltelt időintervallumok hosszát mutatja, a vízszintes tengely az intervallumok számát.

7 ‐ kijelzi az eredményeket számszerű formában. Az első oszlop a mérések sorszámát mutatja, a második a mérés kezdete óta eltelt időt, a harmadik pedig a bütykök észlelése között eltelt időtartamok hosszát adja meg.

Amennyiben 60 mérést végzel:

8 ‐ a táblázat első oldalát mutatja,

2 ‐ a táblázat második oldalát mutatja,

4 ‐ grafikusan mutatja az eredményeket.

A méréssorozatot az előírt számú mérés elvégzése előtt is félbeszakíthatod oly módon, hogy valamelyik gombot megnyomod, és ezek után még egy fél fordulattal megforgatod a korongot.
A motor

25 V

váltófeszültségről működik és a tartólemezén található kapcsolóval indítható el.
A korong és a motor forgórészének teljes tehetetlenségi nyomatéka:

(14, 0 \pm 0, 5) \cdot 10^{- 6} {kgm}^{2}

.
A megoldás menete: A mérési elrendezés vázlatosan a 6. ábrán látható. A számítógép csak a feladatban leírt műveletek végzésére volt alkalmas, ezért a mellékszámításokat csak külön zsebszámológéppel lehetett elvégezni.
A szögelfordulás‐idő grafikon elkészítése egyszerű, hiszen a mérés elvégzése után a függőleges tengelyen csak a képernyőről leolvasott félfordulatok számának

π

-szeresét kell ábrázolni.
A szögsebesség‐idő grafikonnál a függőleges tengelyen a félfordulatok között eltelt idő reciprokának

π

-szeresét kell ábrázolni.
A szöggyorsulás‐idő grafikont a szögsebesség‐idő grafikon numerikus differenciálásával kapjuk.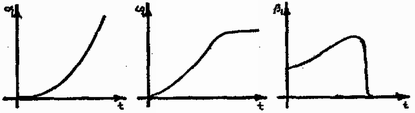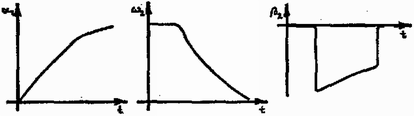

7.a. ábra

7.b ábra

A 7.a ábrán a gyorsulásnál, a 7.b ábrán a lassulásnál kapott grafikonok vázlatos rajzát láthatjuk. A lassulást a huzamosabb ideje működő motor kikapcsolásával lehet mérni.
Feltehetően a gyorsulásnál is ugyanazok a veszteségek vannak jelen, mint lassulásnál. Így a motor forgatónyomatéka:

\begin{matrix} M_{m} = Θ (β_{1} - β_{2}) . \end{matrix}

Az így kiszámított

M_{m}

-et, valamint ennek

ω

-szorosát

ω

függvényében ábrázoljuk. A kapott grafikonok sematikusan a 8. ábrán láthatók.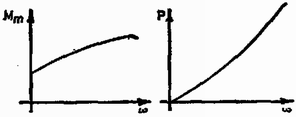

8. ábra

A megoldáshoz hozzátartozik a hibák vizsgálata, és több mérés elvégzése.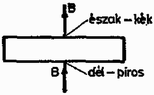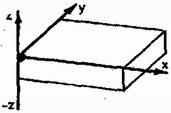

2. Egy fekete dobozban állandó mágneseket rejtettek el. Határozd meg valamennyi mágnes középpontjának térbeli helyzetét és az irányítását! (Ez utóbbit a 9. ábra jelöléseivel értelmezzük.) Az

x

y

és

z

koordinátákat a doboz piros sarokpontjától kell mérned. (L. a 10. ábrát!)

9. ábra

10. ábra

Miután kalibráltad a mérőrendszert, határozd meg a

B

mágneses indukcióvektor

z

komponensét az

(x

y)

síkon

z = 0

mellett!
Mérd meg a külön adott mágnes külső

B

mágneses indukciójának legnagyobb értékét!

Eszközök:

‐ állandó mágnes, amely ugyanolyan, mint az elrejtettek;
‐ változtatható egyenfeszültségű tápegység áramerősség korlátozóval (

0 - 24

V);
‐ indukciós kis tekercs (

1400

menet,

R = 230 Ω

);
‐ tekercspár mágneses tér előállítására, egyenként

8800

menet és

R = 990 Ω

;
‐ fekete doboz rejtett mágnesekkel;
‐ voltmérő (az

1

V-os, a

3

V-os és a

10

V-os méréshatárt ajánljuk);
‐ elektronikus áramkör (javasolt tápfeszültség

24

V), (lásd a 11. ábrát!);
‐ árammérő műszer;
‐ tolóellenállás,

3, 3 k Ω

;
‐ 4 db csatlakozó zsinór;
‐ tartólap, rögzítésre szolgáló lyukakkal;
‐ több célra (pl. a tekercsek rögzítésére) felhasználható gumikarikák;
‐ fogvájók;
‐ vonalzó;
‐ fonál.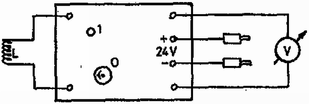

11. ábra

Utasítások: A mágnesek megkeresésére mindenféle rombolásmentes módszer felhasználható. A végső jegyzőkönyvnek tartalmaznia kell az eredményeket, az összefüggéseket, a grafikonokat és a rajzokat. Az általad használt mérési módszer magyarázatára mindig rajzot használj magyarázó szöveg helyett, ha ez lehetséges!
Az indukált feszültség mérésére használható eszköz helyes használata egyértelműen leolvasható a 11. ábráról. Az ábra szerinti berendezés a mágneses térre reagál. A leolvasható maximális feszültség arányos a mágneses fluxusváltozással, amely átmegy a tekercsen. [Az ábrán a nullázó nyomógombot (RESET)

1

-es, a kimenő nulla szintet beállító gombot

0

jelöli.]

A megoldás menete: Célszerű először a mágneses indukcióváltozást érzékelő eszközt hitelesíteni. E célból a kisméretű

1400

menetes tekercs felhasználásával állítsuk össze a 11. ábra szerinti kapcsolást. A hitelesítés a következőképp történik. A kis tekercset a 12. ábra szerinti elrendezésben a két nagy tekerecs közé helyezzük, az eszközt nullázzuk, majd a kis tekercset hirtelen kirántjuk a nagy tekercsek közül. Ekkor a műszeren mutatott feszültség a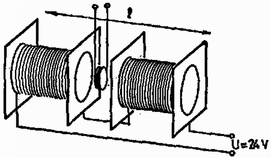

\begin{matrix} Δ B = μ_{0} \frac{N U}{l R} \end{matrix}

mágneses indukcióváltozásnak felel meg, ahol

N

és

R

a két tekercs együttes menetszáma és ellenállása.

12. ábra

A mérőrendszer kalibrálása után határozzuk meg az adott állandó mágnes külső mágneses indukciójának legnagyobb értékét! Ezt legegyszerűbben úgy tehetjük, hogy a mágnes felületének különböző pontjaira helyezzük a kis tekercset, majd onnan hirtelen elrántva leolvassuk a műszeren mutatott feszültséget. A legnagyobb indukciójú helyek a mágnesrúd végének közelében vannak.
Az adott mágnesrudat a közepén fonálra függesztve és a fekete doboz felett mozgatva könnyen megtalálhatjuk a két elrejtett mágnest. Ez a módszer alkalmas a mágnesek pontos helyének meghatározására az

(x

y)

síkban.
Ezután mérjük meg a

B

értékét a

z = 0

síkon a mágnesek környezetében több helyen!
A mért értékek nagyságából következtethetünk arra, hogy milyen közel vannak a mágnesek a mérési helyekhez, azaz meghatározhatjuk a mágnesek

z

irányú elhelyezkedését.