Kezdőlap


Cím:	1985. évi fizika OKTV feladatai
Szerző(k):	Vermes Miklós
Füzet:	1985/október, 322 - 330. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szakközépiskolások számára kitűzött feladatok

Az I. forduló feladatai

1. Hány perccel változna meg a nap hossza, ha a Föld forgási energiája

20 %

-kal csökkenne?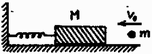

2. Az ábra szerinti vízszintes asztalon egy

D = 100 N/m

rugóállandójú elhanyagolható tömegű feszítetlen rugóhoz erősített

M = 0,1

kg tömegű hasáb fekszik. A hasábbal az ábrán látható módon egy

m = 0,06 kg

tömegű és

v_{0} = 8 m/s

sebességű golyó tökéletesen rugalmatlanul ütközik, és a továbbiakban a két test összetapadva marad.

Adja meg a létrejövő mozgás első két szélső helyzetének távolságát! (A hasáb és a síkfelület közötti súrlódási együttható

μ = 0,5

, a csúszási és tapadási súrlódási együttható között nem teszünk különbséget.)

g = 10 {m/s}^{2}

.
3. Ideális gázt az ábrán

A

-val jelölt állapotból a

C

-vel jelölt állapotba viszünk, az

A \to B \to C

úton. Közben a gáz

50

J hőt vesz fel, és

20

J munkát végez.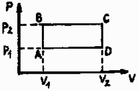

(p_{2} = 2 p_{1})

a) Mekkora a gáz által felvett hő és a végzett munka, ha az állapotváltozást az

A \to D \to C

úton hajtjuk végre?
b) Mekkora lenne az

A \to B \to C \to D \to A

4. Az ábrán látható rendszerben milyen tömegaránynál érvényesül, hogy a két test nem csúszik meg egymáson, ha közöttük a tapadási súrlódási együttható

μ_{t}

? (Tételezzük fel, hogy az asztallap és az

m_{1}

tömegű test között nincs súrlódás és a csigák, fonalak tömege elhanyagolható, valamint a csigák is súrlódásmentesen foroghatnak.)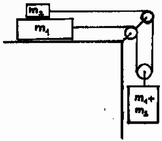

A II. forduló feladatai

1. Üvegkádba vizet töltünk. A kád aljától

h_{1} = 10 cm

-re kétszer domború levegőlencsét rögzítünk. A lencsében a levegőt két

20 - 20 cm

görbületi sugarú, elhanyagolható vastagságú üveg zárja közre. A lencse felülnézetben kör alakú, átmérője

d = 4 cm

. Biztosítjuk, hogy a kád alján, a lencse optikai tengelyén levő

L

pontszerű fényforrás fénye csak a lencsén jusson át a lencse fölötti

h_{2} = 20 cm

magasságú vízrétegbe. (A lencsét megfelelő méretű átlátszatlan lemez közepébe illesztettük.)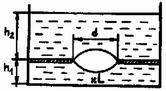

Mekkora a kialakuló folt átmérője

a) a víz felszínén?

b) a víz felszínétől

20 cm

-re levő ernyőn?
(A levegő vízre vonatkoztatott törésmutatója

4 / 3

.)
2. Egyensúlyi állapotban levő héliumgázban a molekulák mozgási energiájának legvalószínűbb értéke csak kétharmad része a rendezetlen mozgáshoz tartozó átlagos mozgási energiának.
a) Mennyi a

- 35^{\circ} C

hőmérsékletű héliumgázban a molekulák sebességének legvalószinűbb értéke?
b) Mennyi egy ilyen sebességű héliummolekula de Broglie hullámhossza?
3. Igen nagy kiterjedésű, elektromosan egyenletesen töltött fémsíkot homogén elektromos mezőbe helyezünk. Ennek hatására a lemez egyik oldalán

E_{1}

, a másikon

E_{2}

térerősségű homogén elektromos mező alakul ki, ahogy az ábra mutatja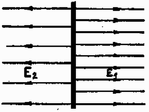

(E_{1} > E_{2})

Határozzuk meg a töltött fémsík egységnyi felületére ható erőt!

4. Függőlegesen lefelé irányuló

B

indukciójú homogén mágneses térben a tér irányára merőleges síkban fekvő

R

sugarú,

A

keresztmetszetű körvezetőben felülről nézve az óramutató járásával egyező irányú

I

erősségű áram folyik.
Mennyivel változik meg a kerület, ha az áramot kikapcsoljuk?
A vezető rugalmassági modulusa:

E

.
(A hőmérsékletet állandó értéken tartjuk.)

A gimnazisták számára kitűzött feladatok és megoldásuk

Az I. forduló feladatai

1. Könnyen gördülő,

M = 5 kg

tömegű kocsin

m = 10 kg

tömegű,

r = 0,2 m

sugarú korong fekszik (1. ábra). A korong peremére vékony fonalat csévéltünk.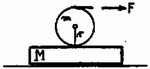

g = 10 {m/s}^{2}

1. ábra

a) Mekkora gyorsulással mozog a korong és a kocsi, ha a fonalat állandó, vízszintes,

F = 100 N

erővel húzzuk és a kocsi, valamint a korong között a súrlódás együtthatója

μ = 0,1

?
b) Mekkora a két test mozgási energiája

L = 2 m

hosszú fonál letekeredése után?
c) Mekkora munkát végeztünk eközben?
(Holics László)

Megoldás. Először meg kell vizsgálnunk a csúszásmentes mozgás feltételét (2. ábra). A korong középpontjának

a

, a kocsinak

A

a gyorsulása. A korongot a húzóerő és a súrlódási erő összege gyorsítja: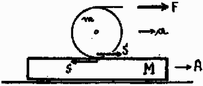

\begin{matrix} F + S = m a . \end{matrix}

2. ábra

Θ

tehetetlenségi nyomatékú korongot az

F

húzóerő és az

S

súrlódási erő nyomatékának különbsége

β

szöggyorsulással forgatja:

\begin{matrix} (F - S) r = β Θ . \end{matrix}

Sima gördülés esetén a szöggyorsulás:

β = \frac{a - A}{r}

A kocsit

S

súrlódási erő

A

gyorsulással gyorsítja balra:

\begin{matrix} A = - S / M . \end{matrix}

A tehetetlenségi nyomaték

Θ = m r^{2} / 2 = 0,2 {kg m}^{2}

. A korong középpontjának gyorsulása az egyenletrendszerből:

\begin{matrix} a = \frac{4 M + m}{3 M + m} \cdot \frac{F}{m} = 12 {m/s}^{2} . \end{matrix}

A súrlódási erő:

S = m a - F = 20

N. A csúszásmentességhez legalább

μ = S / m g = 0,2

nagyságú súrlódási együttható volna szükséges. Mivel a feladatban a súrlódási együttható csak

0,1

, a korong megcsúszik.
a) Csúszás esetében a korong haladó mozgását gyorsító erő:

\begin{matrix} m a = F + μ m g . \end{matrix}

A korong forgására nézve:

(F - μ m g) r = 0,5 m r^{2} β

. A kocsit balra gyorsító erő:

M A = - μ m g

.
Az egyenletrendszer megoldása:

\begin{matrix} A = - 2 {m/s}^{2}, a = 11 {m/s}^{2}, β = 90 s^{- 2} . \end{matrix}

b) A 2 méteres fonál letekeredése közben a korong megtett fordulatainak száma

2 / 2 π r

, minden fordulat

2 π

radiánt jelent, tehát a korong

2 / r = 10

radiánnyi fordulatot tett meg. A kísérlet időtartama

t = \sqrt[]{2 \cdot 10 / β} = 0,471

s, a végső szögsebesség

ω = β t = 42,4 s^{- 1}

. A forgásból származó mozgási energia:

\begin{matrix} E_{f} = 0,5 Θ ω^{2} = 180 J . \end{matrix}

A korong haladásából származó mozgási energia:

\begin{matrix} E_{h} = 0,5 m a^{2} t^{2} = 134,4 J . \end{matrix}

A kocsi mozgási energiája:

0,5 M A^{2} t^{2} = 2,22

J.

Az összes mozgási energia:

316,6

J.
c) A korong útja:

0,5 a t^{2} = 1,22

m, a kötélvég útja

L + s = 3,22

m, az

F

erő által végzett munka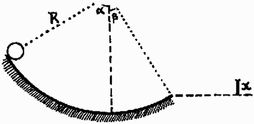

100 N\cdot3,22 m=322 J

2. Adva van egy negyedkörből álló lejtő,

R = 1

α = 80^{\circ}

β = 30^{\circ}

(3. ábra). Egy kis abroncs csúszás nélkül gördül le a bal oldali végről. Milyen

x

magasságig repül a lejtő elhagyása után?

3. ábra

(Vermes Miklós)

Megoldás. Az abroncs tömege

m

, sugara

r

. Helyzeti energiájának csökkenése:

m g R (cos β - cos α)

.
Az abroncs középpontja

v

sebességgel,

ω = v / r

szögsebességgel hagyja el jobb oldalt a lejtőt. Összes mozgási energiája:

\begin{matrix} \frac{m v^{2}}{2} + \frac{ω^{2} Θ}{2} = \frac{m v^{2}}{2} + \frac{v^{2} m r^{2}}{2 r^{2}} = m v^{2} . \end{matrix}

Az energiamegmaradás törvénye szerint:

\begin{matrix} m v^{2} = m g R (cos β - cos α) . \end{matrix}

A középpont sebessége:

v = \sqrt[]{g R (cos β - cos α)}

. A sebesség függőleges összetevője

\begin{matrix} sin β \sqrt[]{g R (cos β - cos α)} . \end{matrix}

Az abroncs ezzel

x

magasságot ér el. Az energiamegmaradás törvényével:

\begin{matrix} m g x = \frac{m \cdot sin^{2} β \cdot g R (cos β - cos α)}{2} . \end{matrix}

A keresett magasság az abroncs adataitól függetlenül:

\begin{matrix} x = \frac{sin^{2} β (cos β - cos α)}{2} \cdot R = 0,0458 m. \end{matrix}

3. Egy zárt tartályban

T_{1}

hőmérsékleten,

p_{1}

nyomáson kétatomos molekulájú gáz van. A gázt

T_{2}

hőmérsékletre melegítjük, ekkor a molekulák

20

%-a szétesik atomokra.
a) Mekkora most a gáz nyomása?
b) Hányszorosára változott a gáz belső energiája? (A molekulák rezgéseitől tekintsünk el!)
(Lugosi Erzsébet)

Megoldás. a) Nyomás tekintetében olyan a helyzet, mintha

20

%-kal több gáz volna jelen, ezért:

\begin{matrix} p_{2} = p_{1} \cdot \frac{T_{2}}{T_{1}} \cdot 1,2. \end{matrix}

b) Eredetileg az energia:

E_{1} = \frac{5}{2} \cdot N k T_{1}

T_{2}

hőmérsékleten:

\begin{matrix} E_{2} = \frac{5}{2} \cdot 0,8 N k T_{2} + \frac{3}{2} \cdot 2 \cdot 0,2 \cdot N k T_{2} = 2,6 N k T_{2} . \end{matrix}

Az energiák aránya:

\begin{matrix} \frac{E_{2}}{E_{1}} = \frac{2,6}{2,5} \cdot \frac{T_{2}}{T_{1}} . \end{matrix}

4. Elektromos mérőműszer feszültségmérési határa

27 Ω

-os előtétellenállást használva

n

-szer nagyobb lesz. A műszert

3 Ω

-os sönttel használva ampermérési határa ugyancsak

n

-szer lesz nagyobb,
a) Mekkora a műszer belső ellenállása?
b) Végkitéréskor a műszer lengőtekercse

9 \cdot 10^{- 4}

wattot fogyaszt. Mennyi végkitéréskor az áramerősség és a feszültség?
(Légrádi Imre)

Megoldás. A lengőtekercs ellenállása

R_{b}

.
a) Az előtétellenállás:

R_{e} = (n - 1) R_{b}

. A sönt ellenállása:

R_{s} = \frac{R_{b}}{n - 1}

; Innen

\frac{R_{e}}{R_{s}} = {(n - 1)}^{2}

, azaz

\frac{27 Ω}{3 Ω} = {(n - 1)}^{2}

, így

n = 4

R_{b} = 3 Ω\cdot(4-1)= 9 Ω

.
b)

P = \frac{U^{2}}{R_{b}}

, így

U = \sqrt[]{R_{b} P} = \sqrt[]{9 \cdot 10^{- 4} W \cdot 9 Ω} = 9 \cdot 10^{- 2} V

\begin{matrix} I = U / R_{b} = \frac{9 \cdot 10^{- 2} V}{9 Ω} = 0,01 A. \end{matrix}

A II. forduló feladatai

1. Egy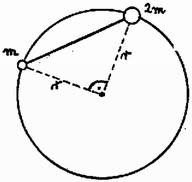

r = 0,5

m sugarú, függőleges síkú karikán két átfúrt golyó csúszhat, tömegeik

m

és

2 m

(4. ábra). A golyókat fonál köti össze. A golyók egy negyedkör végpontjaiban vannak. A súrlódási együtt ható

0,15

. Milyen helyzetben lehetnek a golyók feszített fonál mellett egyensúlyban?

(Nagy László)

4. ábra

Megoldás. A szerkezet helyzetét a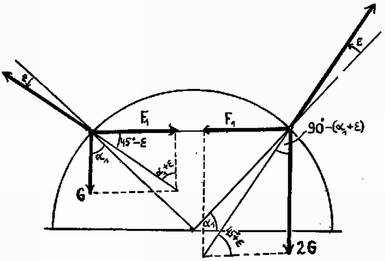

2 m

tömeghez vezető sugárnak a vízszintessel bezárt

α

-szögével határozzuk meg. A súrlódási határszög

ε

. Tudjuk, hogy

tg ε = 0,15

, így

ε = 8, 53^{\circ}

5. ábra

A jobbra történő lecsúszás határhelyzetében a

2 m

nagyságú tömeg helyzetét meghatározó szög

α_{1}

. A tömegekre a

G

és

2 G

súlyerők, az

F_{1}

fonálerő, valamint a pálya által kifejtett kényszererők hatnak. A csúszási határhelyzetben ez utóbbiak

ε

szöggel balrább irányulnak, mint a tömegekhez vezető sugarak (5. ábra). Ekkor a súrlódási erők a

2 m

tömegű test jobbra való lecsúszását akadályozzák. A vektorok háromszögére felírjuk a szinusztételt:

\begin{matrix} \frac{2 G}{F_{1}} = \frac{sin (45^{\circ} + ε)}{cos (α_{1} + ε)}, \\ \frac{G}{F_{1}} = \frac{sin (45^{\circ} - sin ε)}{sin (α_{1} + ε)} . \end{matrix}

Az egyenleteket elosztjuk:

\begin{matrix} 2 = tg (α_{1} + ε) \frac{sin (45^{\circ} + ε)}{sin (45^{\circ} - ε)} . \end{matrix}

ε

értékét behelyettesítve:

\begin{matrix} tg (α_{1} + ε) = 1,4783. \end{matrix}

Így

\begin{matrix} α_{1} = 47, 39^{\circ} . \end{matrix}

A balra történő lecsúszás határhelyzetében a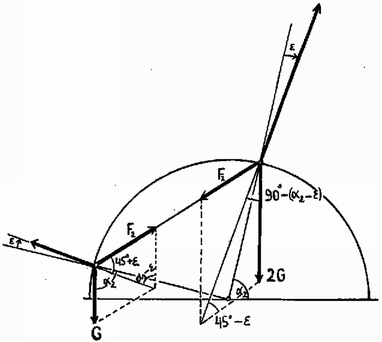

2 m

tömegű testhez vezető sugár vízszintessel bezárt szöge

α_{2}

(6. ábra). Most a pálya által kifejtett kényszererők a sugarak irányához képest

ε

szöggel jobbra irányulnak.

6. ábra

A vektorok háromszögére felírjuk a szinusztételt:

\begin{matrix} \frac{2 G}{F_{2}} = \frac{sin (45^{\circ} - ε)}{cos (α_{2} - ε)}, \\ \frac{G}{F_{2}} = \frac{sin (45^{\circ} + ε)}{sin (α_{2} - ε)} . \end{matrix}

Az egyenleteket egymással elosztva és

ε

értékét behelyettesítve

\begin{matrix} tg (α_{2} - ε) = 2,7057, \end{matrix}

így

\begin{matrix} α_{2} = 78, 25^{\circ} . \end{matrix}

Tehát az egyensúly feltétele az, hogy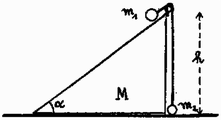

α 47, 39^{\circ}

és

78, 25^{\circ}

között legyen.

α = 36, 87^{\circ}

hajlásszögű,

M = 2 kg

tömegű lejtő szabadon csúszhat vízszintes síkon (7. ábra). A lejtő magassága

h = 1 m

. A lejtő tetejére

m_{1} = 7 kg

tömegű testet helyezünk, a

h

hosszúságú fonál másik végére

m_{2} = 1 kg

tömegű testet erősítettünk. A súrlódás elhanyagolható,

g = 10 {m/s}^{2}

. A rendszert magára hagyjuk. Mennyi idő múlva lesz

m_{1}

és

m_{2}

egymáshoz legközelebb?

7. ábra

(Holics László)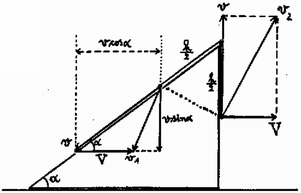

Megoldás. Az

m_{1}

tömegű test lecsúszik a lejtőn. A két test távolsága akkor a legkisebb, amikor a fonál fele futott le a lejtőn, mert a háromszög alapja akkor a legrövidebb, amikor a másik két oldallal egyenlőszárú háromszöget alkot, (amennyiben a másik két oldal összege adott, jelen esetben

h

).
Az

m_{1}

tömegű test lecsúszása közben a lejtő jobbra csúszik. Mindegyik test egyenletesen gyorsuló mozgást végez. A lejtő sebessége a talajhoz képest

V

. Mindkét test sebessége a lejtőhöz viszonyítva

v

. A talajhoz képest az

m_{1}

tömegű test

v_{1}

, az

m_{2}

tömegű test

v_{2}

sebességgel mozog (8. ábra).

8. ábra

m_{1}

tömegű test sebessége a talajhoz képest

v_{1}

, ennek vízszintes összetevője

v cos α - V

. A vízszintes összetevőkre vonatkozóan az impulzusmegmaradás tétele:

\begin{matrix} m_{1} (v cos α - V) = (M + m_{2}) V . \end{matrix}

Ebből

\begin{matrix} V = \frac{m_{1} cos α}{M + m_{1} + m_{2}} \cdot v = 0,56 v . \end{matrix}

Az energiamegmaradás törvényét alkalmazzuk. A lesüllyedő

m_{1}

tömegű test súlyának munkavégzése:

m_{1} g \cdot (h / 2) \cdot sin α

. Ezzel emeli fel az

m_{2}

tömegű testet

h / 2

magasságra és ad az

M

tömegű lejtőnek

M V^{2} / 2

, az

m_{1}

tömegű testnek

m_{1} v_{1}^{2} / 2

, az

m_{2}

tömegű testnek

m_{2} v_{2}^{2} / 2

mozgási energiát:

\begin{matrix} m_{1} g \cdot \frac{h}{2} \cdot sin α = m_{2} g \cdot \frac{h}{2} + \frac{M V^{2}}{2} + \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} . \end{matrix}

Azonban

v_{1}^{2} = {(v cos α - V)}^{2} + {(v sin α)}^{2}

v_{2}^{2} = V^{2} + v^{2}

.
Ezeket, valamint számértékeiket behelyettesítve kapjuk: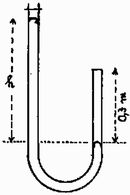

\begin{matrix} 10 V^{2} - 11,2 V v + 8 v^{2} = 32. \end{matrix}

Felhasználva a

V = 0,56 v

összefüggést,

v = 2,565

m/s. Az

m_{2}

tömegű test lejtőhöz viszonyított átlagsebessége

2,565 (m/s) : 2 = 1,2825 (m/s)

, és ezzel a

0,5

méteres utat

0,5 m : 1,2825 (m/s) = 0,38

másodperc alatt teszi meg. Ennyi idő múlva van a két test egymáshoz legközelebb.

3. A bal oldali szárban a higany felett légüres tér, a jobb oldali szárban a higany felett

0,3 m

hosszú légoszlop van (9. ábra). A csapot kinyitjuk. A feltóduló higany az elzárt légoszlopot

0,1 m

-es hosszúságúra nyomja össze. Mekkora volt a csap kinyitása előtt a higanyszintek

h

különbsége? Mekkora az elzárt levegő belső energiájának megváltozása a felemelkedésig?

9. ábra

A kezdeti hőmérséklet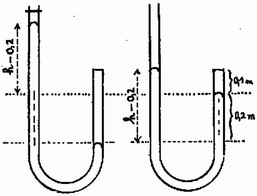

0^{\circ} C

, a külső légnyomás

10^{5}

Pa, a levegő sűrűsége normál állapotban

1,3 {kg/m}^{3}

, állandó térfogat melletti fajhője

700 J/kg \cdot K

, fajhőhányadosa

κ = 1,4

g = 10 {m/s}^{2}

. A higany sűrűsége

ϱ = 13 600 {kg/m}^{3}

. A cső keresztmetszet-területe

2 {cm}^{2}

. Az üveg és higany hőfelvételétől, hővezetésétől tekintsünk el!

(Nagy László)

Megoldás. Kezdeti állapotban az elzárt levegő nyomása (10. ábra):

p_{1} = ϱ g h = 1,36 \cdot 10^{5} (Pa/m) \cdot h

10. ábra

Amikor az elzárt levegő térfogata a legkisebb lesz, akkor a nyomása

p_{2}

. Az adiabatikus változás törvénye szerint:

\begin{matrix} p_{2} = p_{1} \cdot {(\frac{0,3 m}{0,1 m})}^{1,4} = 1,36 \cdot 10^{5} (Pa/m) \cdot h \cdot 4,656 = 6,33 \cdot 10^{5} (Pa/m) \cdot h . \end{matrix}

A gáz hőmérsékletét ekkor a gáztörvénnyel számítjuk:

\begin{matrix} \frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}, T_{2} = T_{1} \cdot \frac{p_{2} V_{2}}{p_{1} V_{1}} = 424 K . \end{matrix}

A levegő hőmérsékletének emelkedése:

424 - 273 = 151 K

.
A bezárt levegő normáltérfogata

V_{0} = p_{1} V_{1} / p_{0} = 8,16 \cdot (10^{- 5} m^{2}) \cdot h

, tömege

(1,3 {kg/m}^{3}) \cdot 8,16 \cdot (10^{- 5} m^{2}) \cdot h = 1,06 \cdot (10^{- 4} kg/m) \cdot h

. A bezárt levegő belső energiájának növekedése:

\begin{matrix} Δ E = (700 J/kg K) \cdot 1,06 \cdot (10^{- 4} kg/m) \cdot h \cdot (151 K) = (11,2 J/m) \cdot h . \end{matrix}

Mivel adiabatikus változásról van szó, a levegő belső energiájának növekedését a külső légköri levegő nyomásának és a leeső higanynak a munkavégzése okozta.
A külső légköri levegő

p_{0}

nyomás mellett

(2 \cdot 10^{- 4} m^{2}) \cdot (0,3 - 0,1) m=4\cdot10^{- 5}m^{3}

térfogatváltozást okozott, ezért munkavégzése

(10^{5} {J/m}^{3}) \cdot (4 \cdot 10^{- 5} m^{3}) = 4 J

.
A leeső higany munkavégzését a következőképp számíthatjuk: A vonalkázással jelölt

0,2 m

hosszú higanyoszlop változatlan magasságban maradt. A

h - 0,2

m hosszú higanyoszlop minden részecskéje

0,2

métert esett, ezért a munkavégzés:

\begin{matrix} (2 \cdot 10^{- 4} m^{2}) \cdot (h - 0,2 m) \cdot (13 600 {kg/m}^{3}) \cdot g \cdot (0,2 m) = (5,44 J/m) \cdot h - 1,088 J . \end{matrix}

A belső energia növekedését egyenlővé tesszük a munkavégzések összegével:

\begin{matrix} (11,2 J/m) \cdot h = 4 J + (5,44 J/m) \cdot h - 1,088 J; \end{matrix}

innen a keresett eredeti magasság:

h = 0,51

m.
A levegő belső energiájának növekedése:

(11,2 J/m) \cdot (0,51 m) = 5,71 J

.
A feladatban szereplő végállapot nem jelent egyensúlyt, a bezárt csőben levő higany valamelyest visszaesik.

III., kísérleti forduló

A versenyzőknek az volt a feladatuk, hogy egy négyszögjelet adó generátor adatainak a kapcsolásban szereplő ellenállásoktól való függését megvizsgálják.

Az 1985. évi tanulmányi verseny eredménye

A szakközépiskolai tanulók eredménye

1. díj: Mészáros László (Miskolc, Bláthy O. Villamosip. Szki., IV. o. t., tanára: Tepliczky István)

2. díj: Miró József (Bp., Corvin M. Híradástechn Szki., III. o. t., tanára: Gőghné Béres Katalin)

3. díj: Borsi Ferenc (Debrecen, Mechwart A. Gépip. Szki., III. o. t., tanára: Dr. Kopcsa József)

További helyezettek:
4. Tóth Péter (Debrecen, Erdey-Grúz T. Vegyip. Szki., III. o. t., t.: Nyeste Elek), 5. Boros Zoltán (Zalaegerszeg, Dimitrov Építőip. Szki., IV. o. t., t.: Vas Gyuláné), 6. Pócz Zoltán (Jászberény, Erősáramú Szki., IV. o. t., t.: Bakki Árpád), 7. Farkas István (Bp., Petrik L. Vegyip. Szki., IV. o. t., t.: Kiss Jolán és Finta András), 8. Szép Attila (Debrecen, Mechwart A. Gépip. Szki., IV. o. t., t.: Dr. Kopcsa József), 9. Mudra István (Debrecen, Erdey-Grúz T. Vegyip. Szki., III. o. t., t.: Nyeste Elek), 10. Kettinger Zoltán (Székesfehérvár, Ságvári E. Szki., IV. o. t., t.: Feczkó János), 11. Baráth János (Bp., Petrik L. Vegyip. Szki., IV. o. t., t.: Kiss Jolán).

A III. osztályos gimnáziumi tanulók eredménye

1. díj: Jakovácz Antal (Bp., Apáczai Csere J. Gyak. Gimn., tanára: Kelemen László)

2. díj: Leisztinger Tamás (Bp., Apáczai Csere J. Gyak. Gimn., tanára: Kelemen László)

3. díj: Csegezy Zsolt (Pannonhalma, Bencés Gimn., tanára: Hirka Antal)

A további helyezettek: 4. Aczél Ákos (Bp., II. Rákóczi F. Gimn., t.: Marcsek Gábor), 5. Horváth Róbert (Veszprém, Lovassy L. Gimn., t.: Horváth Péter), 6. Porgányi Gergely (Bp., Apáczai Csere J. Gyak. Gimn., t.: Holics László), 7. Bősze Tibor (Bp., Fazekas M. Gyak. Gimn., t.: Horváth Gábor), 8. Kiss Miklós (Zalaegerszeg, Zrínyi M. Gimn. t.: Németh László), 9. Kovács Róbert (Kecskemét, Katona J. Gimn., t.: Németh Ágnes), 10. Lajos Gábor (Eger, Gárdonyi G. Gimn., t.: Ardó Jánosné és Leitner Györgyné)
Elsőfokú dicséretet 7, másodfokú dicséretet 9 tanuló kapott.

A IV. osztályos gimnáziumi tanulók eredménye

1. díj: Limbek Csaba (Bp., Fazekas M. Gyak. Gimn., tanára: Tóth László)

2. díj: Grőbler Tamás (Bp., Berzsenyi D. Gimn., tanára: Hubert Györgyné)

3. díj: Hargitai Zsolt (Sopron, Széchenyi I. Gimn., tanára: Légrádi Imre)

A további helyezettek: 4. Keszthelyi Róbert (Bp., Fazekas M. Gyak. Gimn., t.: Tóth László), 5. Szalaí Tamás (Székesfehérvár, Teleki B. Gimn., t.: Bakó Béláné és Mihályi Gyula), 6. Benyó Zoltán (Bp., Fazekas M. Gyak. Gimn., t.: Tóth László), 7. Szakáll István (Bp., Apáczai Csere J. Gyak: Gimn., t.: Valovics István), 8. Fecsó Péter (Bp., Berzsenyi D. Gimn., t.: Hubert Györgyné), 9. Wildwerger Zoltán (Bp., Kaffka M. Gimn., t.: Jäger Csaba), 10. Zsenits Balázs (Bp., Apáczai Csere J. Gyak. Gimn., t.: Flórik György)
Elsőfokú dicséretet 4, másodfokú dicséretet 23 tanuló kapott.

Vermes Miklós