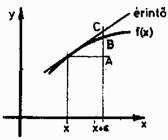Cím: Közelítő számítások a fizikában
Szerző(k):  Gnädig Péter 
Füzet: 1985/március, 130 - 138. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy matematikai probléma megoldásánál, vagy egy tétel bizonyításánál beszélhetünk tökéletes pontosságról, végtelen sok számjeggyel megadott tizedes törtekről, közelítésmentes gondolatmenetről. Be tudjuk bizonyítani például azt, hogy 2 irracionális szám, vagy hogy végtelen sok prímszám létezik, sőt, még azt is, hogy a szögharmadolás problémája általában nem oldható meg körzővel és vonalzóval.
Ezzel a "tiszta'', közelítésmentes matematikával szemben a fizikai problémák megfogalmazásánál, feladatok megoldásánál, mérések kiértékelésénél kivétel nélkül minden esetben közelítéseket kell alkalmaznunk. Ezek a közelítések lehetnek fizikai jellegűek (ilyenekkel általában a vizsgált jelenséget leíró fizikai törvény megfogalmazásánál, az egyenletek felállításánál van dolgunk), de lehetnek matematikai jellegűek is (ez utóbbiakat akkor alkalmazzuk, ha nélkülük a feladat megoldása túlságosan bonyolult, vagy éppen teljes egészében keresztülvihetetlen volna). Fizikai jellegű közelítés például az, amikor egy mesterséges hold keringési idejének kiszámításakor elhanyagoljuk a légellenállást, vagy amikor egy villanyvasaló teljesítményének meghatározásakor a hálózati csatlakozó vezeték ellenállását nullának vesszük. Ezeknél a közelítéseknél mérlegelnünk kell, hogy a jelenségnek melyik része lényeges és melyik része az, amelyet nyugodtan elhanyagolhatunk. Egy mérésnél végig kell gondolnunk, hogy milyen pontosságot kívánunk (és tudunk) elérni, ennél a pontosságnál milyen mellékeffektusok hagyhatók figyelmen kívül, illetve hogy miként lehetne ezeket a zavaró tényezőket csökkenteni, vagy a hatásukat figyelembe venni és ezzel a mérés pontosságát növelni. Ezek meglehetősen bonyolult kérdések, az elhanyagolások mögött általában komoly fizikai megfontolások rejtőznek. Többnyire egyszerre kell áttekintenünk a fizika különböző, egymástól távol eső területeit (hőtant és mechanikát a súrlódási jelenségek tárgyalásánál, elektromágneses hullámokat és a kristályfizikát a lézer működésének megértésénél stb.), ezért nehéz, de ugyanakkor szép és érdekes is a fizikusok munkája.
A matematikai közelítésekkel sokkal egyszerűbb a helyzet. Legtöbbször elfeledkezhetünk a probléma fizikai hátteréről (bár néha nem árt, ha mégsem tesszük ezt), és az egyenletek megoldásának matematikai nehézségeire összpontosíthatjuk figyelmünket. Alkalmazhatjuk a matematikusok által kidolgozott összefüggéseket, amelyek ‐ az algebrai átalakítások vagy az egyenletrendezés "játékszabályaihoz'' hasonlóan ‐ mindig, minden körülmények között érvényesek. Matematikai közelítés például az, ha egy kicsiny szög szinuszát a szögnek ívmértékben mért nagyságával helyettesítjük,vagy ha 2,999972-t 9-nek vesszük.
Természetesen a kétféle közelítő eljárásnak egymással összhangban kell állnia. Nem érdemes egy durva, erősen leegyszerűsített fizikai modell egyenleteit 10 tizedesjegy pontossággal megoldanunk (pl. ha egy nagy magasságból eső test mozgását a légellenállás elhanyagolásával számoljuk). De akkor sincs sok értelme a nagyon pontos számításnak, ha ugyan az egyenleteink a legjobb tudásunk szerint tökéletesen pontosak (ilyen például az elektrosztatikában a Coulomb-törvény), de a szükséges adatok (a töltések nagysága és távolsága) csak 10% pontossággal mérhetők! A fordított eset is előfordulhat: hiába pontosítjuk a legfinomabb effektusok figyelembevételével egy jelenség leírását, ha a probléma matematikai része ezáltal annyira elbonyolódik, hogy teljesen kezelhetetlenné válik (ez lenne a helyzet akkor, ha egy gáz minden egyes molekulájára külön-külön felírnánk a Newton-féle mozgásegyenletet).
Az alábbiakban a matematikai jellegű közelítések játékszabályaival fogunk megismerkedni, majd a fizika különböző területeiről választott példákon keresztül mutatjuk be. hogyan működik mindez a gyakorlatban.

 

Közelítő számítás ‐ pontosan
 
Nézzünk először néhány egyszerű matematikai problémát, és próbáljunk meg ezeken keresztül megbarátkozni a közelítő számítások furcsa szabályaival! Hogyan lehetne például kiszámítani az
x=16,00000008+2
kifejezés számértékét? Egy átlagos pontosságú zsebszámológép csak 16-t tudja kiszámítani, de a tizedik jegyben a nyolcast már nem tudja figyelembe venni. Függvénytáblázatokkal sem boldogulunk, hiszen azok még pontatlanabbak. Közelítőleg azonban meg tudjuk mondani a keresett mennyiséget, hiszen 16,00000008≈16 (körülbelül egyenlő), tehát
x≈16+2x≈6.
Sajnos nem tudjuk, hogy a végeredményben a ≈ jel mit jelent. Úgy érezzük, hogy mivel a gyök alatt a 10. jegyben "csaltunk'', az eredmény is kb. 10 jegyre pontos, de 9 jegyre biztosan jó, tehát az "igazi'' és a közelítő végeredmény eltérése a kiszámított x-hez viszonyítva 10-9, vagy  10-10 nagyságrendű. Ha tehát az eredményt csupán 1%, vagy 1% pontossággal keressük, úgy nyugodtan vehetjük x-et 6-nak.
Vegyünk most egy kicsit bonyolultabb esetet, legyen a kiszámítandó mennyiség
x=16,0000000816,00000008-4,
amelynek számértékére 1% pontossággal lenne szükségünk. Ha ismét az előző közelítést alkalmazzuk, a nevezőbe nulla kerül, ami nyilván értelmetlen! Adjuk fel a kérdést egy különlegesen (mondjuk 12 jegyre) pontos számítógépnek. (A feladatot nemsokára mi is meg tudjuk oldani, ráadásul akár fejben is!) Válaszul
16,00000008=4,000000010000-t
kapunk, a nevezőbe tehát 0,000000010 kerül, így x értéke
4,0000000100,000000010=400000001,0≈4⋅108.
Az utolsó ≈ jel annak felel meg, mintha a számlálóban a gyököt 4-gyel közelitettük volna.
Miért alkalmazható ugyanaz a közelítés a kiszámítandó kifejezés egyik részében, ami értelmetlenségekre vezet máshol? Egy számítás során mit, mikor, hogyan és miért közelíthetünk? Ilyen jellegű kérdésekkel gyakran kerülünk szembe fizikai (és matematikai) feladatok megoldásánál. Sokszor úgy érezzük, nem jártunk el következetesen: egy kicsiny mennyiséget az egyik helyen elhanyagoltunk, máshol viszont figyelembe vettük ugyanazt. Az előző példában jó eredményt kaptunk, de hátba más esetben nem szabad ugyanígy eljárnunk. Hogyan lehetne kicsit precízebben nyomon követni, mit is csinálunk tulajdonképpen?
Rossz közérzetünket az = és a ≈ jelek közötti különbség okozta. Egyenletek megoldása során mindig egyenlőségjelet használunk, s azonos átalakítások sorozata után eljutunk a végeredményhez, ami azt mutatja, hogy x pontosan egyenlő egy bizonyos számmal. A valóságban azonban (a kezdeti adatok pontatlansága és a kerekítési hibák miatt) mindvégig körülbelül egyenlő jelet kellett volna írnunk, és ez a jel a végeredményben nem feltétlenül ugyanazt a pontatlanságot jelöli, mint a kiindulásnál szereplő ≈ jel.
Próbáljuk meg a ≈ jelet felcserélni a jól ismert és megszokott egyenlőségjellel, de oly módon, hogy közben ne mondjunk le a közelítés nyújtotta előnyökről!
 

16,00000008≈16 helyett írjunk 16,00000008=16+ "egy kicsiny számot''!
 
Ezzel természetesen csak akkor nyerünk valamit, ha azt is megmondjuk, hogy ez a "kicsiny szám'' mennyire kicsiny. Jelen esetben 0,00000008 egy 10-8 nagyságrendű (vagy esetleg 10-7 nagyságrendű) szám, nagysága "néhányszor'' 10-8. Nem szükséges megmondanunk, hogy éppen 8-szor 10-8, hiszen ha így tennénk, akkor visszatérnénk a "pontos'' számításhoz; ehelyett elegendő csupán a nagyságrendjét számon tartanunk. Erre a nagyságrendre a latin ordó (rend) szó alapján bevezették a következő jelölést:
16,00000008=16+O(10-8)
(ejtsd: ordó tíz a mínusz nyolcadikon). Ezzel pontosan megadtuk, hogy mennyire közelítő a számításunk, mennyire tér el egymástól a közel egyforma két mennyiség, mekkora az eltérés nagyságrendje.
Ezentúl
x≈yhelyett azt írjuk, hogyx=y+O(ε),
ahol ε egy kicsiny szám, nagysága a közelítés pontosságára utal. Az ordó szó helyett nyugodtan gondolhatjuk, sőt mondhatjuk is a "néhányszor'' szót. Azt, hogy a néhányszor mit jelent, azt ε kicsinysége dönti el. Általában a 0,1 és a 10 közötti számokra mondhatjuk, hogy néhány (vigyázat: a néhány itt most nem feltétlenül egész szám).
Milyen számolási szabályok érvényesek az ordó szimbólumra?
Általában érdektelen számunkra O(x) előjele, hiszen csak a hiba nagyságrendjét jelzi. Ezért -O(x) helyett +O(x)-et írhatunk, továbbá O(-x)=O(x).
Nyilván érvényes, hogy
y⋅O(x)=O(y⋅x).

Számolásaink során felhasználjuk, hogy
O(x)=O(2x),
hiszen néhányszor x= néhányszor 2x. Hasonlóan láthatjuk be, hogy
O(nx)=O(x),
ha O(n)=1, vagyis n se nem túl nagy, se nem túl kicsiny szám. Felhasználhatjuk továbbá, hogy
O(xy)=O(x)⋅O(y),
valamint
O(x+y)=max [O(x),  O(y)],
tehát O(x) és O(y) nagyobbika, feltéve, hogy x és y azonos előjelű.
Az utóbbi összefüggések csak addig érvényesek, amíg nem ismételjük őket túlságosan sokszor, hiszen ha O(2x)=O(x), akkor O(4x)=O(x) is igaz, és így tovább, de O(128x) már nem egyenlő O(x)-szel. Ezt a jelenséget hibahalmozódásnak nevezik, és a másodpercenként több százezer műveletet végző számítógépeknél komoly problémát jelenthet. Szerencsére nekünk, mivel csak rövidebb számításokat akarunk végezni, nem lesz gondunk vele.
Mielőtt rátérnénk a fizikai alkalmazásokra, ismerkedjünk meg egy hasznos matematikai összefüggéssel. Gyakran előfordul, hogy egy 1-hez közeli számnak valahányadik hatványát kell kiszámítanunk, tehát (1+ε)n-t keressük, ahol ε egy kicsiny szám. Első (legdurvább) közelítésben ez a kifejezés 1-gyel egyenlő, és az elkövetett hiba ε nagyságrendű, azaz
(1+ε)n=1+O(ε).
Általában ennél pontosabban kell számolnunk, azaz szükségünk van az ε rendig pontos eredményre, és csak O(ε2) hibát engedhetünk meg. Szorozzuk össze az alábbi n tényezőt:
(1+ε)⋅(1+ε)⋅...⋅(1+ε)=1+nε+O(ε2).
Érdekes, hogy ez az összefüggés nemcsak pozitív, hanem negatív, sőt még tört kitevőkre is igaz. Például
1(1+ε)2=(1+ε)-2=1-2ε+O(ε2),
hiszen ha mindkét oldalt megszorozzuk (1+ε)2-tel, az
1=[1+2ε+ε2][1-2ε+O(ε2)]=1+2ε-2ε+O(ε2)
összefüggést kapjuk, ami a megkövetelt ε2 nagyságrendű pontosságig valóban azonosság. Hasonlóan láthatjuk be a
1+ε=(1+ε)1/2=1+12ε+O(ε2)
összefüggés helyességét, négyzetre emelés után ugyanis
1+ε[1+12ε+O(ε2)]2=1+ε2+ε2+O(ε2)
adódik, ami valóban fennáll.
A fentiek segítségével most már könnyen ki tudjuk számítani a bevezetőben szereplő 16,00000008-4 kifejezés értékét, hiszen
16,00000008=16+8⋅10-8=41+1210-8==4[1+1410-8+O(10-16)]=4+1⋅10-8+O(10-16),


tehát
16,00000008-4=1⋅10-8+O(10-16).

A matematikai előkészítés után térjünk rá a fizikai alkalmazásokra! Olyan példákat választottunk, amelyeknél jól felhasználhatjuk a közelítések biztonságos kezeléséből adódó előnyöket. A feladatok nem olyan sorrendben követik egymást, ahogyan az egyes témakörökkel a középiskolában megismerkedünk, hanem inkább nehézségi sorrendben. Ha valamelyik példa fizikai háttere ismeretlen lenne az Olvasó előtt, nyugodtan ugorja át azt a feladatot és válasszon olyat, amelynek "fizikáját'' már ismeri.
 

1. példa: Két egyenlő nagyságú, de ellentétes előjelű elektromos töltés egymástól d távolságban helyezkedik el. Határozzuk meg az általuk keltett elektromos erőtér nagyságát a töltéseket összekötő egyenes mentén, de tőlük nagy távolságban!
 

Megoldás: Egy Q nagyságú töltés r távolságban a Coulomb-törvénynek megfelelően
E1=Qr2
nagyságú elektromos térerősséget hoz létre.
 
 
1. ábra
 

A -Q töltésű test tere r+d távolságban
E2=-kQ(r+d)2.
Használjuk ki, hogy r sokkal nagyobb d-nél! Nyilván E2 közelítőleg -kQr2-tel egyenlő, amennyiben a nevezőben r mellett elhanyagoljuk d-t. Az így elkövetett hiba d/r nagyságrendű, vagyis
E2=-kQr2[1+O(dr)],
az eredő elektromos tér pedig
E=E1+E2=-kQr2[1-1+O(dr)]=0+O(kQdr3).
Sajnos az eredménynek csak a nagyságrendjét kaptuk meg, mivel a pontosan kiszámított tagok éppen kiejtették egymást. Nyilván ennél többre vágyunk, szeretnénk az eredményt számszerűen is meghatározni, még ha ez a szám nem is egyezik meg tökéletesen pontosan az "igazi'' térerősséggel. Eljárásunkat úgy finomíthatjuk, ha E2-t egy kicsit pontosabban számítjuk ki, nem olyan durván, mint azt fentebb tettük. E2-t megadó képlet nevezőjéből r2-et kiemelve alkalmazhatjuk az 1-hez közeli számok hatványaira megismert összefüggést:
E2=-kQr2[1+dr]-2=-kQr2[1-2dr+O(d2r2)].
Ez a számítási pontosság már elegendően finomnak látszik, mert ha a legnagyobb tagok kiejtik egymást, még mindig marad egy pontosan (értsd: számszerűen) kiszámított mennyiség, és csak ezután következik a közelítés pontosságára utaló ordó-szimbólum. Az eredő térerősség:
E=E1+E2=kQr2[1-1+2⋅dr+O(d2r2)]=2kQdr3+O(kQd2r4),

amely ‐ mint látjuk ‐ a távolság köbével fordított arányban (tehát a ponttöltések Coulomb-terénél gyorsabb ütemben) csökken, a töltésrendszert pedig a dipólnyomatéknak nevezett Qd szorzat jellemzi. Nagy távolságban a ki nem számolt tag 2kQd/r3 mellett valóban elhanyagolható.
 

2. példa: Határozzuk meg egy R sugarú gömbtükör fókusztávolságát, vagyis annak a pontnak a helyzetét, ahová a tükör a tengelyével párhuzamosan érkező sugarakat összegyűjti! Teljesül-e a képalkotás feltétele?
 
 
2. ábra
 

Megoldás: Nézzük meg, hol metszi az optikai tengelyt az a fénysugár, amely eredetileg a tengelytől h távolságban haladt! Amennyiben az így kapott f távolság minden h-ra ugyanakkora, úgy a leképezés tökéletes. Nagy nyílásszögű, pl. félgömb tükörre ez nem teljesül, hiszen például a h≈0 és a h≈R esetek élesen elkülönülnek. Szorítkozzunk ezért kicsiny nyílásszögű tükrökre, vagyis legyen h≪R! Ilyenkor az f(h) függvény is körülbelül állandó, f értékei alig változnak. Mit jelent a "körülbelül'', illetve az "alig'' kifejezés ebben az esetben? Egy girbegörbe tükörnél is kicsiny (tehát a nullától és emiatt egymástól is alig különböző) h értékekre f(h) sem változhat sokat, f értéke O(h) pontosságig állandó. A képalkotáshoz ez még kevés! Ennél pontosabban, legalább O(h2), precízebben fogalmazva (hiszen f hosszúság dimenziójú kell legyen) O(h2/R) hibahatáron belül állandó (h-tól független) kell legyen f(h). Vajon teljesül- e ez a jelen esetben? Az ábráról leolvasható, hogy
x=R-f,h=Rsinα,h=xsin2α.
Ezeket összevetve
h=(R-f)⋅2⋅h2R21-h2R2,
vagyis
1=2R(R-f)[1+O(h2R2)]
adódik, ahonnan
f(h)=R2+O(h2R).
Mivel ez a függvény nem tartalmaz h-val arányos, vagyis O(h)-s tagot, a képalkotás feltétele teljesül, és a tükör fókusztávolsága R/2-nek vehető.
 

3. példa: Egy elejtett testet a sebességének négyzetével arányos közegellenállási erő fékez: Fk=-εv2. Mennyi idő alatt esik le a test H magasságból? (A közegellenállási erő az esés során végig nagyon kicsiny a súlyerőhöz képest, ezért elegendő ε-ban első rendig, azaz ε első hatványának figyelembe vételéig számolni.)
 

Megoldás: A test mozgásegyenlete a Newton-féle törvény szerint
mg-εv2=ma.
Első közelítésben ε-t, pontosabban az ε-nal arányos tagot elhanyagolhatjuk, ekkor a szabadesés összefüggései alkalmazhatók:
s=g2t2,v=gt,
az esés ideje pedig
T=2Hg.
Az elkövetett hiba minden tagban O(ε). (A rövidebb írásmód kedvéért csak ε hatványait tartjuk számon a közelítések pontosságának becslésénél, az ε mellett álló és többnyire dimenziós mennyiségeket nem írjuk ki.)
Próbáljuk meg most ε első hatványának pontosságáig valamennyi mennyiséget precízen kiszámítani, s csak az O(ε2)-et hanyagoljuk el!
s=g2t2+εf(t)+O(ε2),v=gt+εvf(t)+O(ε2),a=g+εaf(t)+O(ε2).
ahol f(t) egyelőre ismeretlen függvény, vf=ΔfΔtésaf=ΔvfΔt pedig az ennek megfelelő sebesség, illetve gyorsulás. A fenti kifejezéseket visszahelyettesítve a mozgásegyenletbe
mg-ε[g2t2+O(ε)]=mg+ε⋅maf+O(ε2)
adódik. (Figyeljük meg, hogy a fékezőerő képletében a sebességet elegendő az első ‐ a szabadesésnek megfelelő ‐ közelítésből adódó gt-vel helyettesítenünk, hiszen a v2-et szorzó kicsiny ε miatt a valódi sebesség és gt eltéréséből adódó hiba csak ε2 rendben rontja el az egyenletet.)
A közegellenállásból adódó gyorsulás tehát
af=-g2mt2+O(ε2),
ahonnan visszakövetkeztethetünk vf , abból pedig f(t) alakjára. Mivel általánosan igaz, hogy egy  y=xn alakú függvény változási sebessége (deriváltja)
ΔyΔx=(x+Δx)n-xnΔx=xnΔx=[(1+Δxx)n-1]==xnΔx[1+nΔxx2+O(Δx2x2)-1]=nxn-1+O(Δx),


az idő négyzetével arányos gyorsulás esetén a sebesség t33 -mal, az f(t) függvény pedig t412-vel kell hogy arányos legyen. Így végül az
s(t)=g2t2-ε⋅g2t412m+O(ε2)
út‐idő függvényt kapjuk, ahonnan az esés T idejére a
H=g2T2-ε⋅g212mT4
összefüggést kapjuk. Nem szükséges azonban ezt a (T2 -re nézve másodfokú) egyenletet pontosan megoldanunk, hanem csupán ε pontosságig. Hogyan tehetjük ezt meg? Alkalmazzuk az előbb már bevált "trükköt'', írjuk fel, hogy az esés ideje durván
T2=2Hg+O(ε),
majd rendezzük át a precízebb számolásból adódott egyenletet
T2=2Hg+εg6mT4+O(ε2),
alakra. Ezzel még ‐ a hagyományos értelemben ‐ nem oldottuk meg az egyenletet, hiszen annak mindkét oldalán előfordul a T ismeretlen. Ha azonban figyelembe vesszük, hogy T2 -et  ε pontosságig már ismerjük, és hogy T4 előtt úgyis van már egy kicsiny szorzótényező, akkor máris előttünk áll a megoldás:
T2=2Hg+εg6m[2Hg+O(ε)]2=2Hg+23εH2mg+O(ε2),
ahonnan
T=2Hg1+ε2H3m=2Hg[1+εH6m+O(ε2)].

Az itt bemutatott eljárást perturbációszámításnak nevezik. Segítségével módszeresen finomíthatjuk eljárásunkat, és az egyes lépéseknél mindig csak az előző, durvább közelítés eredményére van csak szükségünk.
 

A közelítések és a differenciálszámítás kapcsolata
 

Befejezésül röviden megemlítjük, hogy miként használható fel a differenciálszámítás a közelítő számításoknál. Általában ott jutunk nehéz helyzetbe, ahol két majdnem pontosan azonos mennyiség különbségét szeretnénk meghatározni. Ilyen esettel találkoztunk az 1. példában is, ahol a keresett mennyiség az
1(r+d)2-1r2
volt. Ezt a különbséget felfoghatjuk úgy is, mint az f(x)=1x2 függvénynek két közeli pontjában felvett függvényértékek különbségét.
 
 
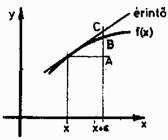3. ábra
 

Általában az
f(x+ε)-f(x)
megváltozás felírható
f(x+ε)-f(x)ε⋅ε
alakban is. A tört (ha ε elegendően kicsiny) jól közelíthető az f(x) függvény deriváltjával:
f(x+ε)-f(x)ε≈f'(x),

precízebben:
f(x+ε)-f(x)ε=f'(x)+O(ε),
így tehát a keresett különbség
f(x+ε)-f(x)=ε⋅f'(x)+O(ε2).
Geometriailag ez a közelítés annak felel meg, hogy a 3. ábrán az AB szakasz hosszát AC-vel helyettesítjük.
Ennek felhasználásával
1(r+d)2-1r2=(1r2)'⋅d+O(d2)=-2r3d+O(d2).
Hasonlóan adódik, hogy kicsiny szögek szinusza
sinε=sin(0+ε)-sin0=εcos0+O(ε2)=ε+O(ε2).
(Ráadásul, mivel sinx páratlan függvény, a hibatag nem is ε2, hanem ε3 nagyságrendű csupán). A kapott összefüggés természetesen nem tekinthető a sinx≈x közelítő képlet "levezetésének'', hiszen felhasználtuk, hogy (sinx)'=cosx. Általában éppen fordítva járunk el, a közelítés helyességének belátása vezet el a derivált függvény meghatározásához. Itt most csupán arra kívántunk rámutatni, hogy ha valahonnan (mondjuk táblázatból) ismerjük egy függvény deriváltját, akkor ennek segítségével könnyen tudunk közelítő számításokat végezni ezzel a függvénnyel.
Mint láttuk, a közelítő számításoknak éppen olyan jól definiált, pontosan megfogalmazható szabályai vannak, mint például az algebrai átalakításoknak, vagy a geometriai szerkesztéseknek. Ne tekintsük tehát a közelítő számításokat a precíz matematika mostohagyermekének, ne szégyelljünk élni a közelítések adta lehetőségekkel, de mindig legyen előttünk, hogy milyen nagyságrendű tagokat hanyagoltunk el, vagyis hogy mit, miért és mennyire közelítettünk!
 

Feladat: Határozzuk meg egy lövedék röppályáját a közegellenállás figyelembevételével! Számítsuk ki, hogy egy 30∘-os szögben kilőtt lövedék hány méterrel messzebb repülne, ha nem fékezné a levegő! (A hiányzó adatokat vegyük fel tetszés szerinti, de reálisan elképzelhető nagyságúnak!)