Kezdőlap


Cím:	1984. évi Eötvös Loránd Fizikaverseny
Szerző(k):	Vermes Miklós
Füzet:	1985/február, 81 - 84. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat 1984. október 27-én rendezte 61. versenyét Budapesten és 12 vidéki városban az abban az évben érettségizettek és középiskolai tanulók részére. A versenyzők 5 órai munkaidő alatt oldhatták meg a három feladatot. Bármely segédeszközt használhattak, beleértve a zsebszámítógépet is. A versenyen 180 dolgozatot adtak. be. Ismertetjük a feladatokat és a verseny eredményét.

1. Vízszintes síkhoz törésmentesen csatlakozó lejtőről kisméretű,

m

tömegű testet csúsztatunk le egy

M

tömegű kocsira, amelyre középen félhengerpalást van erősítve (1. ábra). A kis test felcsúszik a félhengeren és éppen a félhenger tetején csökken a test és a pálya közötti erő zérusra. A kis test ezután függőlegesen, szabad eséssel éppen a kocsi szélére esik.

A súrlódás elhanyagolható.
a) Milyen hosszú a kocsi?
b) Milyen

h

magasságból csúszott le a test?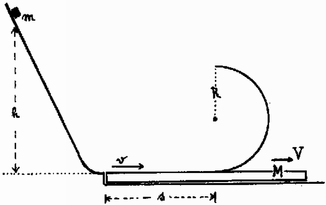

1. ábra

(Holics László)

Megoldás. Először azt határozzuk meg, hogy mekkora

v

sebességgel kell az

m

tömegű kis testet a kocsira csúsztatni, hogy felülről függőlegesen, szabadeséssel essen le. Azután kérdezzük: hol esik a test a kocsira?
Amíg a kocsira csúszott test a kocsi vízszintes részén fut, addig a kocsi nem mozdul meg, hiszen nincs súrlódás. Amikor a körlejtőn fut, akkor nyomja a kocsit.
A körpálya tetején az

m

tömegű kis testnek nincs sebessége a talajhoz viszonyítva, viszont a kocsi

V

sebességgel fut. A kis test impulzusát megkapja a kocsi:

\begin{matrix} m v = M V, vagyis V = (m / M) \cdot v . \end{matrix}

A kis test akkor hagyja el éppen a félkörpálya tetején a pályát, ha a centripetális gyorsulás épp a

g

nehézségi gyorsulással egyenlő. (A centripetális gyorsulás értékét a kis test kocsihoz viszonyított

V

sebességéből kell meghatározni):

\begin{matrix} g = V^{2} / R . \end{matrix}

V

-nek az impulzustörvényből adódó értékét felhasználva és az egyenletet rendezve:

\begin{matrix} v^{2} = R g {(M / m)}^{2} . \end{matrix}

Ez az összefüggés tartalmazza az impulzus megmaradását és azt a körülményt, hogy a felső pontban az

m

tömegű test szabadesést végez.
Az energiatörvény értelmében

v

-nek olyan nagynak kell lennie, hogy a kis test

m v^{2} / 2

mozgási energiája épp fedezni tudja a felemelkedéshez szükséges munkavégzést és a kocsi mozgási energiáját.

\begin{matrix} \frac{m v^{2}}{2} = m g \cdot 2 R + \frac{M V^{2}}{2} . \end{matrix}

V

-nek a felső pontbeli szabadesésből következő értékét felhasználva és az egyenletet rendezve

\begin{matrix} v^{2} = R g (M / m) + 4 R g . \end{matrix}

A kocsira érkezés

v

sebességének az előzőekben kapott két feltételnek kell eleget tennie.

v^{2}

kifejezéseit egyenlővé téve:

\begin{matrix} R g {(M / m)}^{2} = R g \cdot (M / m) + 4 R g . \end{matrix}

Innen a

M / m

tömegviszonyra az alábbi egyenletet kapjuk:

\begin{matrix} {(M / m)}^{2} - M / m - 4 = 0. \end{matrix}

Az egyenlet számunkra használható megoldása:

\begin{matrix} \frac{M}{m} = \frac{1 + \sqrt[]{17}}{2} = 2, 562. \end{matrix}

A feladat lényeges és érdekes eredménye: a kísérlet csak akkor sikerülhet, ha a kis test és a kocsi tömegének aránya ennyi, függetlenül a félkörpálya sugarától (és

g

-től).
A tömegviszony értékét felhasználva

\begin{matrix} v^{2} = \frac{9 + \sqrt[]{17}}{2} \cdot R g . \end{matrix}

h

indítási magasságra nézve

m g h = m v^{2} / 2

, tehát

\begin{matrix} h = \frac{9 + \sqrt[]{17}}{4} \cdot R = 3, 281 R . \end{matrix}

2 R

magasságból történő esés ideje

2 \sqrt[]{R / g}

, így a kocsi útja az esés ideje alatt:

\begin{matrix} s = 2 \sqrt[]{R / g} \cdot V = 2 \sqrt[]{R / g} \cdot \sqrt[]{R g} = 2 R, \end{matrix}

a kocsi teljes hossza ennek kétszerese, tehát

4 R

. A kocsi hosszát a tömegviszony ismerete nélkül is ki lehet számítani. Igazolható, hogy ha a

M / m

arányra kapott feltétel teljesül, akkor a számított adatok mellett a kísérlet valóban végrehajtható.

2. A henger fala és a dugattyú rúdja tökéletesen hőszigetelő (2. ábra). A dugattyú anyaga valamelyest hővezető. Kezdő állapotban mindegyik térfélben

1

‐

1 mol

hélium van,

237 K

hőmérsékleten. El lehet-e érni a dugattyú mozgatásával, hogy valamelyik térrészben

120 K

-re csökkenjen a hőmérséklet?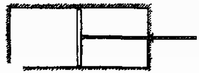

2. ábra

(Károlyházy Frigyes)

Megoldás. Adiabatikus változásokra kell gondolnunk. Erre nézve Poisson törvénye érvényes:

p_{1} V_{1}^{κ} = p_{2} V_{2}^{κ}

, illetőleg a gáztörvény felhasználásával:

\begin{matrix} T_{1} V_{1}^{κ - 1} = T_{2} V_{2}^{κ - 1} . \end{matrix}

Hélium esetében

κ = 5 / 3

és

κ - 1 = 2 / 3

.
A henger két részének térfogatát

V_{1}

-gyel és

V_{2}

-vel jelölve, a dugattyú balra mozgatásával az elgondolható legszélső esetben

V_{2}

az eredeti

V

-nek kétszerese lesz. Ekkor a kiterjesztett jobb oldali térrészben a hőmérséklet

273 : 2^{2 / 3} = 172 K

lenne, ami nem elég nagy lehűlés. De ez a lépés sem hajtható végre, hiszen a bal oldali térrész térfogata nem lehet nulla.
Két lépésre van szükség. Először vigyük a dugattyút gyorsan a bal oldali térrész negyedébe. Ekkor a két térrészben

\begin{matrix} a térfogatok: & 0, 25 V, & 1, 75 V, \\ a hőmérsékletek: & 688K, & 188K, \\ a nyomások: & 10, 1atm, & 0, 39atm. \end{matrix}

Ezután várjuk meg a hőmérséklet kiegyenlítődését, ami lehetséges, hiszen a dugattyú anyaga kissé hővezető. A létrejövő közös hőmérséklet a számtani középérték, mert a gázok tömege egyenlő. A hőmérséklet mindegyik térrészben

438 K

lesz. Ezután átlökjük a dugattyút a jobb oldali térfél negyedébe, ekkor

\begin{matrix} a térfogatok: & 1, 75 V, & 0, 25 V, \\ a hőmérsékletek: & 120K, & 1602K, \\ a nyomások: & 0, 25atm, & 23, 5atm. \end{matrix}

Ezzel elértük a kívánt lehűtést. Amennyiben nagyobb térfogatváltozásokat hozunk létre, a lehűlés még nagyobb. Ismételt dugattyúmozgatással az eredmény mindig rosszabb lesz, mert minden mozgatással munkát végzünk, ami emeli az átlaghőmérsékletet.

3. Egy párhuzamosan elhelyezett lemezekből álló kondenzátor fel van töltve (3. ábra). A lemezek alsó széle alatt kis iránytű áll. Ezután a lemezek tetejére helyezett pálcával a kondenzátort kisütjük. Hogyan viselkedik a kisülés közben az iránytű?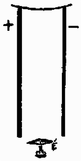

3. ábra

(Radnai Gyula)

Megoldás. A pálcában haladó kisütő áram a jobbkéz-szabály szerint az északi pólust a papír síkjára merőlegesen befelé nyomja mágneses erejénél fogva. A feladat lényege azonban az ún. eltolási áram szerepének tisztázása.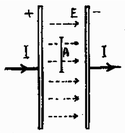

4. ábra

Maxwell a múlt század második felében feltételezte, hogy az elektromos térerő időbeli változása a közönséges elektromos áramhoz hasonlóan mágneses erőket okoz a környezetében. Vizsgáljunk egy kondenzátort, amelyet

I

áram folyamatosan feltölt (4. ábra)! Ezen

I

áram a környezetében mágneses erőket hoz létre. Közben a kondenzátor terében az

E

elektromos térerő időben folyamatosan növekszik. Maxwell feltételezte, hogy az

A

felszínű felületre merőleges, időben változó elektromos térerő olyan mágneses teret hoz létre környezetében, mint az

ε_{0} A \cdot (d E / d t)

amper erősségű áram, amely esetünkben megegyezik a kondenzátort töltő vagy kisütő áram erősségével. Az állítás helyességét a kísérleti nehézségek miatt nem lehet közvetlenül megvizsgálni. Azonban az eltolási áram feltételezésével levezethető az elektromágneses hullámok tulajdonsága, és ezeket a tapasztalat igazolja. Így az időben változó elektromos térerő áramszerű viselkedésének létezése bizonyított.
Feladatunkban a balról jobbra mutató elektromos térerő időben csökken, az ún. eltolási áram a lemezek közötti térben jobbról balra mutat. Ennek mágneses ereje az északi pólust a jobbkéz-szabály szerint a papír síkjából ki akarja emelni, ellentétesen a pálca áramának hatásával. Kérdés, melyik hatás erősebb. Ha például feltételezzük, hogy a kondenzátor lemezei kör alakúak, akkor az eltolási áram a tér minden részében közelebb van az iránytűhöz, mint a pálca, ezért hatása erősebb: az iránytű északi pólusa ki akar emelkedni a papír síkjából.

A verseny eredménye

I. díjat kapott Kós Géza, a budapesti Berzsenyi Dániel Gimnázium III. o. tanulója: Koltai Márta.

II. díjat hárman kaptak egyenlő helyezésben: Csillag Péter, a budapesti Műszaki Egyetem Villamosmérnöki Karának hallgatója, aki Budapesten a Landler Jenő Híradástechnikai Szakközépiskolában érettségizett; tanárai Darányi László és Szakács László voltak, Czigler Zoltán honvéd, aki a budapesti Radnóti Miklós Gyakorló Gimnáziumban érettségizett mint Stróbel Mária tanítványa és Fáth Gábor honvéd, aki a budapesti Fazekas Mihály Gyakorló Gimnáziumban érettségizett mint Horváth Gábor tanítványa.

III. díjat ketten kaptak egyenlő helyezésben: Fodor Gyula, a budapesti Eötvös Loránd Tudományegyetem Természettudományi Karának fizikus hallgatója, aki a budapesti Móricz Zsigmond Gimnáziumban érettségizett mint Tarnócziné Gedeon Melitta tanítványa, és Németh-Buhin Ákos, a budapesti Fazekas Mihály Gyakorló Gimnázium IV. osztályos tanulója, tanára Tóth László.

Dicséretet hárman kaptak egyenlő helyezésben: Frigó József honvéd, aki Pécsett a Nagy Lajos Gimnáziumban érettségizett mint Tornyos Tivadar tanítványa, Rácz Attila, a budapesti Semmelweis Orvostudományi Egyetem hallgatója, aki a soproni Berzsenyi Dániel Gimnáziumban érettségizett mint Nagy Márton tanítványa, és Szakállas Gyula honvéd, aki Zalaegerszegen a Zrínyi Miklós Gimnáziumban érettségizett mint Gádor Győzőné tanítványa.
Vermes Miklós

Az Eötvös verseny 2. feladatához kapcsolódik az alábbi feladat, amelynek megoldását a következő számban közöljük:

A henger fala (és a dugattyú rúdja) tökéletesen hőszigetelő, a dugattyú anyaga valamelyest hővezető. Kezdetben mindegyik térfélben

1

‐

1 mol

hélium van

T_{0} = 273 K

hőmérsékleten. A dugattyú igen lassú mozgatásával a henger bal oldali részének térfogatát

V_{0}

- ról

V'_{1}

-re csökkentjük. Mennyi ezután a hélium hőmérséklete a hengerben?
(Radnai Gyula)