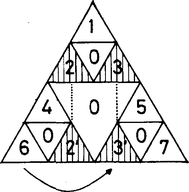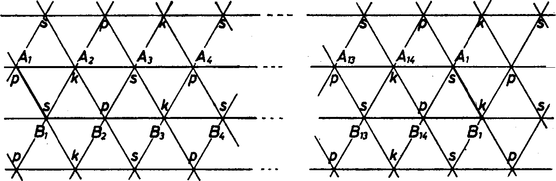|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Ha a Pascal-háromszög első négy sorát a szokásos módon felírjuk, majd az egymás alá kerülő számokat összeadjuk, akkor a következő hét számot kapjuk: , , , , , , .
Ha a Pascal-háromszög első 1024 sorát írjuk fel és az egymás alatt álló számokat összeadjuk, akkor az így adódó 2047 szám között hány páratlan lesz?
I. megoldás. a) Írjunk a Pascal-háromszögben a páratlan számok helyébe 1-et, a párosak helyébe 0-t. Ekkor a képzési szabályt annyiban kell módosítani, hogy 1+1 helyett a következő sorban 0-t kell írnunk annak megfelelően, hogy két páratlan szám összege páros. A következőkben a módosított háromszöget a módosított képzési szabállyal fogjuk Pascal-háromszögnek nevezni.
Felírva valameddig a háromszöget, a következő szerkezetet vehetjük észre: ha 2n számú sort írunk fel, akkor az utolsó sor csupa 1-esből áll, és a következő 2n sorban két 2n sorból álló Pascal-háromszög keletkezik egymás mellett, közöttük pedig csupa 0 (1. ábra). Belátjuk teljes indukcióval, hogy ez minden n-re igaz.
 1. ábra
Világos, hogy n=1-re igaz az állítás (már n=0-ra is).
Tegyük fel, hogy n-nek valamilyen k értékére a 2k-adik sorban csupa 1-es áll, szám szerint 2k darab. Ekkor a következő sor két szélén 1-es áll, köztük pedig 2k-1 darab nulla. A további sorokban a 0-k száma egyesével csökken, a két szélén pedig egy-egy újabb Pascal-háromszög keletkezik egymástól függetlenül addig, míg a köztük levő 0-k el nem fogynak. Ez a 2k-adik lépésben következik be. Az ez alatt kialakult két Pascal-háromszög utolsó sora feltevésünk szerint csupa 1-esből áll, tehát a 2k+1 sorból álló Pascal-háromszög utolsó sora is csupa 1-esből áll. A tulajdonság tehát öröklődik. Ezzel beláttuk, hogy fennáll minden n-re.
b) Felírva n néhány kezdő értékére a 2n sorból álló háromszöget, az oszlopok szerinti összegzés a következő eredményeket adja (a fölső sorba a sorok számát, alá az oszlopösszegek páros vagy páratlan voltát jelző 0, 1-ek sorozatát írtuk):
2021222311,1,11,1,0,1,0,1,11,1,0,1,1,0,1,1,1,0,1,1,0,1,1
Azt látjuk, hogy középen mindig 1-es áll, odáig balról 1, 1, 0 ismétlődik periodikusan, jobbról 0, 1, 1; páros hatvány esetén nincs töredék hármas, páratlan hatványnál viszont a középső 1-es mellé még egy-egy hármas első, illetőleg utolsó 1-ese kerül.
Belátjuk teljes indukcióval, hogy az oszlopösszegek szerkezete, ha 2n sorú háromszög oszlopait összegezzük, minden n-re ilyen. Az első néhány n értékre már láttuk, hogy ez igaz.
Az is világos, hogy középen 1-nek kell állnia, akárhány sor után összegezünk is, hiszen a háromszögek a)-ban megállapított szerkezete szerint az első sor egyetlen 1-ese alá a továbbiak során mindig 0 kerül.
Tegyük fel, hogy n valamilyen k értékére igaz az állítás. Összegezzük a 2k+1 sorból álló háromszöget úgy, hogy külön összegezzük az első 2k sort és külön a többit, majd a két keletkező összegsort is összegezzük. Ezt kívántuk jelezni a 2. ábrán. Az a) rész szerint a második sorban kétszer ismétlődik az első sorbeli sorozat; a középső 1-esek az első sor első 1-ese előtti, ill. az utolsó 1-es utáni hely alá kerülnek.
 2. ábra
Ha most k páros, akkor az 1, 1, 0 hármasok alá 0, 1, 1 hármasok kerülnek, ill. a jobb oldalon megfordítva. Ezekből összegezve 1, 0, 1 lesz. Így a végeredmény a következő: 1, 1, 0 hármasok következnek az alsó sorban a bal oldali középső 1-esig, majd ez után 1, 0, 1 hármasok. De akkor az elsőhöz hozzácsatolva a középső1-est, továbbra is 1, 1, 0 hármasok következnek, míg a felső sor középső 1-ese előtt marad még külön egy 1-es. Hasonlóan a jobb oldalán is marad egy 1-es, majd 0, 1, 1 hármasok következnek. Ezzel épp a páratlan kitevőre vonatkozó szerkezetet kaptuk.
Ha viszont k páratlan, akkor a fölső sor szélső 1-eseit válasszuk külön. Ezek után 1, 0, 1 hármasok következnek mindkét oldalról egészen a középső 1-esig. A bal oldalon az első 1-es alatt az alsó sorozat középső 1, 1, 1 hármasának az utolsó 1-ese áll, utána pedig az 1, 0, 1 hármasok alatt 0, 1, 1 hármasok. Így összegzéskor csupa 1, 1, 0 hármasokat kapunk a középső 1-esig. Jobbról ennek a tükörképe áll, így ebben az esetben a páros kitevőnek megfelelő szerkezet adódott. Ezzel a bizonyítást befejeztük.
A feladat 210, tehát a páros hatvány számú sor utáni összegezés esetén kérdezi a páratlan oszlopösszegek számát. Ekkor 2046/3 összeghármas keletkezik 2‐2 páratlan összeggel, és ehhez járul még a középső páratlan összeg, ami együtt 1365 páratlan összeget ad.
Megjegyzés. Általában ha 2n sor leírása után összegezünk, akkor a keletkező 2n+1-1 összeg közt, ha n páros, eredményünk szerint páratlan szám van, míg páratlan n esetén a páratlan oszlopösszegek száma A két eredmény egybefoglalható a következő formulában:
II. megoldás. Az I. megoldás a) részét felhasználjuk. Legyen n≥2 és a 2n+1 számú sor utáni összegzést bontsuk két részre, mint az előző megoldásban, de a fellépő 3 Pascal-háromszög összegzését még bontsuk fel feleakkora háromszögek összegzésére, amint a 3. ábra mutatja.
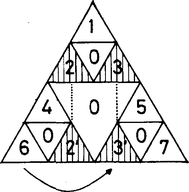 3. ábra
A 0-kból álló háromszögeket figyelmen kívül hagyhatjuk. Ugyancsak nem kell figyelembe venni a 2 és 2', továbbá a 3 és 3' jelű háromszögeket sem, mert ezekben azonos oszlopok állnak egymás alatt, így összegük mindig páros számot ad. A megmaradó háromszögek közül az 1 jelűnek, a 4 és 6 jelű párnak, továbbá az 5 és 7 jelűből állónak nincs közös oszlopa, így ezekre a részekre külön-külön végezhetjük az összegzést.
Módosítsunk ezen még annyit, hogy a 6 jelű háromszöget áthelyezzük a 3' jelű helyére. Ezzel azok az oszlopai, amelyek a 4 valamelyik oszlopa alatt álltak, az 5 azonos oszlopa alá kerülnek, így az oszlopösszegek nem változnak. Így végül két 2n-1 sorú és egy 2n sorú Pascal-háromszög oszlopait kell összegeznünk. Jelöljük f(n)-nel a 2n sorú Pascal-háromszög oszlopösszegei közt a páratlan számok számát, akkor meggondolásunk azt adta, hogy Tudva még, hogy f(0)=1, f(1)=3, sorra meghatározhatjuk az egymás utáni helyeken f értékeit. Úgynevezett rekurzív meghatározást nyertünk f értékeire. f(10)-re természetesen ismét 1365 adódik.
Megjegyezzük, hogy a közbenső függvényértékeket megfigyelve ebből is megsejthetjük, és a nyert összefüggés alapján teljes indukcióval bebizonyíthatjuk a fenti megjegyzésben nyert formulát f(n)-re.
III. megoldás. Meggondolásunkat kicsit egyszerűsíti az a megjegyzés, hogy a Pascal-háromszög sorait folytathatjuk mindkét irányban nullákkal. Ekkor az egy 1-est és kívüle csupa 0-t tartalmazó első sorból elindulva a továbbiak mind úgy keletkeznek, hogy az egyes helyekre a balra és jobbra fölöttük levő szám összegét írjuk.
Megvizsgáljuk, hogy ha valamelyik soránál megállva oszloponként összegezzük az egymás alatt álló számokat, milyen kapcsolat olvasható le ebből a képzési szabályból az egymás mellett álló összegekre. Nézzük először a középső oszlopot. Erre tükrös a Pascal-háromszög, hiszen ha tükrözünk rá, az első sor sem változik meg és a képzési szabály is érvényben marad. Ebben az oszlopban legfelül az első sor egyetlen 1-ese áll, alatta csupa páros szám, hiszen mindegyik két tükrös helyzetű, tehát egyenlő szám összege. A középső oszlop összege tehát akármelyik sorig páratlan szám.
Ha a középsőtől különböző olyan oszlopot nézünk, amelyiknek van eleme az utolsó sorban, akkor az oszlop minden eleme a két szomszédos oszlop egy-egy elemének az összege, és a szomszédos oszlopok minden eleme szerepel összeadandóként. Így a kérdéses oszlopösszeg a két szomszédos oszlopösszegnek az összegével egyenlő. Az olyan oszlopokra, amelyeknek az utolsó eleme az utolsó előtti sorban áll, megállapításunk akkor volna érvényes, ha még egy sor kiírása után végeznénk az összegezést. Az ilyen oszlopösszegek tehát a szomszédos oszlopösszegek összegénél kisebbek a következő sornak a kérdéses oszlopba eső elemével.
A Pascal-háromszög m-edik sorában a 0-tól különböző számok az (m-1k), 0≤k≤m-1 binomiális együtthatók. Ezekre fennáll a következő összefüggés (lásd az alábbi 1. megjegyzést):
Ha 2-hatvány sorszámú sor után végezzük az összegezést, akkor az összegekre talált összefüggés szerint a következő sor elemeinek a párosságát kell ismernünk. Belátjuk azonban, hogy ennek minden eleme páros a két szélen álló 1-es kivételével, s így levonása nem változtatja meg az összeg páros vagy páratlan voltát. Valóban, az (1) összefüggésből, ha m=2n, akkor a jobb oldalnak is oszthatónak kell lennie 2n-nel. Mivel pedig k a 2-nek csak n-nél alacsonyabb hatványával lehet osztható, mert 1≤k≤2n-1, így (2nk) is páros kell hogy legyen.
A középső oszlopra vonatkozó szimmetria miatt elég azt megállapítani, hogy az az előtti oszlopok összegei között hogyan oszlanak el a páros és páratlan összegek.
Az első nem csupa 0-ból álló oszlop utolsó eleme 1, afölött csupa 0 áll, így az összeg is 1, tehát páratlan. Mivel az előtte álló oszlopösszeg 0, az utána állónak páratlannak kell lennie, hogy az összegük 1 legyen. A következő oszlopösszeg páros, mert közte és az első oszlop között páratlan összegű oszlop áll. A levonandó következő sorbeli elem, mint láttuk, az összeg párosságát nem változtatja meg. Ez után viszont újra páratlan összeg következik, mert a kettővel előbbi páratlan összeghez adva, páros eredményt kell adnia. Ezzel a kiindulási helyzethez: páros összeg után páratlan, jutottunk vissza, s így ismétlődik, amit eddig találtunk: páratlan, páratlan, páros összegek következnek egészen a középső előtti oszlopig, a középsőben mindig páratlan az összeg, onnan pedig az odáig talált összegek következnek fordított sorrendben.
Ezzel az I. megoldás b) részében talált eredményre jutottunk, amiből az ott látott módon következtethetünk tovább.
Megjegyzések. 1. Az (1) összefüggés könnyen nyerhető számítással, de belátható kombinatorikus meggondolással is. Egy m-tagú társaság k-tagú küldöttséget akar kijelölni, köztük egy szószólóval. Ekkor kiválaszthatják a szószólót m-féleképpen és mellé a k-1 tagot a maradó m-1-ből (m-1k-1)-féleképpen. Így a bal oldali kifejezés adódik a lehetőségek számára. Eljárhatnak azonban úgy is, hogy kiválasztják a k embert (mk)-féleképpen, és azok maguk közül választanak egy szószólót, ami k-féleképpen lehetséges. Így a jobb oldal is ugyanezeknek a lehetőségeknek a számát adja.
2. A fentiekhez hasonlóan 2 helyett tetszés szerinti p prímszámra és pozitív egész n-re lehet látni (1)-ből, hogy (pnk) osztható p-vel, ha 1≤k≤pn-1. Ebből viszont a képzési szabály alapján következik, hogy az előző sor számai felváltva 1 és p-1 maradékot adnak p-vel osztva. Ennél valamivel több is igaz: ha 1≤a≤p-1, akkor (apn-1k) nem osztható p-vel. Ezt úgy látjuk be, mivel tudjuk, hogy egész számról van szó, hogy felírjuk olyan tört alakjában, amelyiknek a számlálója egyszerűsítés után nem osztható p-vel: | (apn-1k)=apn-11⋅apn-22⋅...⋅apn-kk. |
Itt a választása miatt a kivonandó p-nek legfeljebb akkora hatványával osztható, mint a kisebbítendő (ez lehet természetesen a 0-adik hatvány is), tehát a különbség akkora hatványával, mint a kivonandó, ami egyben a nevező is. Ekkor azonban egyszerűsítés után a szorzat számlálója valóban nem osztható p-vel (természetesen a nevező sem).
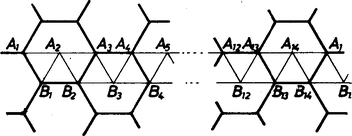
2. Az A1B1A2, B1A2B2, A2B2A3, ..., B13A14B14, A14B14A1, B14A1B1 egymáshoz csatlakozó merev szabályos háromszöglapok, melyek az A1B1, B1A2, ..., A14B14, B14A1 élek mentén hajtogathatók. Elvégezhető-e a hajtogatás úgy, hogy a 28 háromszöglap egy síkban legyen?
I. megoldás. Ha a feladatban leírt felület síkba hajtogatható, pl. az A1A2B1 háromszög síkjába, akkor a többi háromszög ezt a háromszöget tartalmazó háromszögrács egy-egy háromszögét fogja fedni. Ha a hajtogatás sikerült, akkor vágjuk fel az összehajtogatott felületet az A1B1 él mentén és hajtogassunk tovább, amíg az összes többszörös fedést meg nem szüntetjük. Így egy paralelogrammához jutunk. Ez utóbbi hajtogatások a síknak a rács egy-egy egyenesére való tükrözésével valósíthatók meg. Rajzoljuk meg azt a két szabályos hatszöget, amelyiknek egyik oldala A1B1 és az ehhez csatlakozó hatszögrácsot a síkban (4. ábra).
 4. ábra
Figyeljük meg, hogy bármelyik tükrözésnél ez a hatszögrács önmagába megy át, tehát a kiterítés után az A1B1 él másodszori képe is hatszögoldalra, sőt párhuzamos hatszögoldalra kellene hogy kerüljön. A sávba eső párhuzamos hatszögoldalak közt azonban 6-6 szabályos háromszög van, 28 pedig nem osztható 6-tal, tehát a keletkező felület nem lehet síkba hajtogatható.
II. megoldás. Az egyes háromszögek AiAi+1, ill. BiBi+1 oldallal párhuzamos középvonalai zárt törtvonalat alkotnak a térben. Síkba hajtogatva ezek továbbra is zárt törtvonalat alkotnak, tehát mint vektoroknak ‐ alkalmasan irányítva ‐ az összegük a nulla-vektor. Két egymás utáni vektornak az iránya vagy megegyezik, vagy, ha a köztük levő él mentén hajtogatás történt, egyik vagy másik irányban 120∘-ot zárnak be egymással (5. ábra). A zárt törtvonal egyes szakaszai tehát az egymással 120∘-ot bezáró és egyenlő hosszú a, b vagy c vektorral egyenlők. Legyen r az a vektorok száma, s a b-ké, t a c-ké, akkor tudjuk, hogy | a+b+c=0,ra+sb+tc=0,r+s+t=28. |
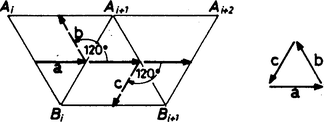 5. ábra
Az első két egyenletből pl. c-t kiküszöbölve és átrendezve az egyenlethez jutunk. Mivel a és b nem párhuzamos, ez csak úgy lehet, hogy
r-t=t-s=0,azazr=s=t,s így3r=28
a harmadik egyenletből. Ez azonban nem lehet, mert r' egész szám. A felület tehát nem hajtogatható egy síkba.
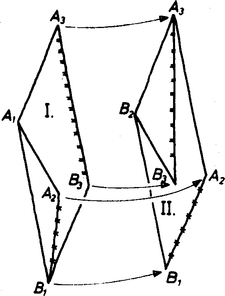
III. megoldás. Ha a feladatban szereplő felület síkba hajtogatható, akkor síkba kiterített hálója is (6. ábra) összehajtogatható úgy, hogy a két A1, ill. B1 pont egymásra kerüljön.
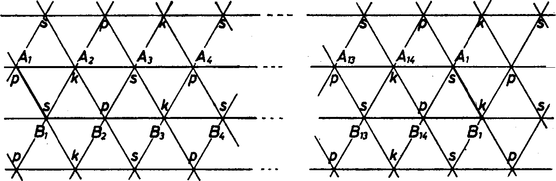 6. ábra
Minden hajtásnál a háló háromszögei a hálót tartalmazó háromszögrács egy-egy háromszögébe mennek át. Színezzük az A1, B1, A2 csúcsokat sorra pirosra, sárgára és kékre. Ekkor folytathatjuk a színezést a három színnel úgy, hogy az egész háló és az egész azt tartalmazó síksáv háromszögeinek a csúcsai különböző színűek legyenek. Az A1, A2, ... pontok sorozata periodikusan ismétlődve piros, kék, sárga színű lesz, a B1, B2, ... pontok pedig sárga, piros, kék színűek. Ezután tükrözve az A-k, ill. B-k egyenesére, majd sorra a keletkező újabb határvonalakra az egész háromszögrács összes csúcsainak olyan színezését kapjuk három színnel, amelynél minden háromszög csúcsai különböző színűek. Ha most a rács bármelyik egyenesére tükrözünk, minden csúcs ugyanolyan színű csúcsba megy át. Ahhoz tehát, hogy a kívánt hajtogatás lehetséges legyen, a két A1-gyel jelzett csúcsnak egyszínűnek kellene lennie, azonban az egyik piros, a másik sárga. A kívánt hajtogatás tehát nem lehetséges.
IV. megoldás. Vizsgáljuk az A1B1A2B2A3...A14B14A1 zárt törtvonalat. Ennek két-két szomszédos szakasza mindig egy háromszöglap két éle, tehát 60∘-ot zár be. A felület háromszögei a sík egy szabályos háromszögrácsának a háromszögeibe kerülhetnek csak.
 7. ábra
Jelöljünk meg egy csúcsot, ahová A1 kerül (7. ábra). Ekkor B1 annak a szabályos hatszögnek egyik csúcsába kerül, amelyiknek a megjelölt csúcs a középpontja, A2 pedig valamelyik szomszédos csúcsába, mert a szomszédos szakaszok 60∘-ot zárnak be. B2 ezután vagy újra a megjelölt csúcsba kerül, vagy annak a hatszög valamelyik oldalára vonatkozó tükörképébe. Jelöljük meg ezeket is. Az eljárás most már ismételhető. A következő két pont ismét egy megjelölt pont körüli szabályos hatszög két szomszédos csúcsába kerül, a harmadik vagy egy már megjelölt pontba kerül, vagy egy ilyennek a körülötte levő hatszög valamelyik oldalára vonatkozó tükörképébe. Jelöljük meg ezeket is. Ilyen módon minden harmadik szakasz végpontja kerül megjelölt pontba, tehát pl. a 27. szakasz végpontja. Ekkor azonban a 28. szakasz végpontja nem kerülhet A1-be. A kívánt hajtogatás tehát nem lehetséges.
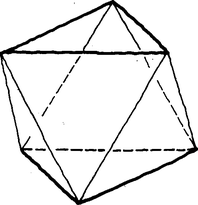
Megjegyzések. 1. Láttuk, hogy ahhoz, hogy, a keletkező felület síkba hajtogatható legyen, a háromszögek számának oszthatónak kell lennie 6-tal. Többen állították, hogy ez elegendő is. Ez így már csak azért sem igaz, mert a 6 háromszögből álló felület egy oktaéder, amelyiknek két szemközti lapját eltávolítottuk, és ez merev a két lap eltávolítása után is (8. ábra).
 8. ábra
Arra is gondolni kell, hogy a felületnek a feladatbeli leírása (most már 28 helyett 6k darab háromszöggel, ahol k legalább 2) nem egyértelmű, hiszen elkészítve a hálót, a két A1B1 él összeragasztása előtt még meg is csavarhatjuk, akár többször is. A 9. és 10. ábra egy-egy síkba hajtogatott, 6k háromszögből álló szalagot mutat, és alatta ‐ hajlékony anyagból képzelve el őket ‐ térben is szemléltettük alakjukat.
 9. ábra
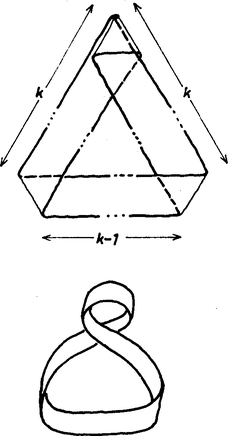 10. ábra
Az már kérdéses, hogy a síkbeli zárt karika 3-dimenziós felületté hajtogatható-e csak a megengedett élek menti hajtogatással. Az, hogy ez nem magától értetődő, látható abból is, hogy az oktaéder-felületnek megfelelő szalag is megvalósítható a síkban. A jobb elképzelés kedvéért két részben rajzoltuk meg a felületet. A 11. ábra két rombusza fölé kell hajtani a hozzájuk csatlakozó háromszöget, majd az I rombuszt a II-re helyezni és az egyformán jelölt (és betűzött) éleket összeragasztani. Ha ez 3-dimenziós felületté volna hajtogatható a háromszögek hajlítása nélkül, akkor megfordítva, az oktaéder-felület is síkba volna hajtogatható, de az, mint említettük, merev. Még meglepőbb eredményre jutunk, ha az I rombuszhoz csatlakozó háromszöget a rombusz alá hajtjuk, úgy helyezzük egymásra a két rombuszt és ragasztjuk össze az egymásnak megfelelő éleket. Így egy megcsavart szalagot kapunk síkba hajtogatva (12. ábra). Ennek megfelelő 3-dimenziós felület merev háromszögekből egyáltalán nem készíthető.
 11. ábra
 12. ábra
2. Többen állították, hogy a 3k háromszögből álló szalag is síkba hajtogatható, ha k≥2. Ez az állítás már azért is kétes értékű, mert a feladat szövege páros számú háromszögre utal. Megtehetjük azonban, hogy pl. eggyel kevesebb B pontot veszünk, mint A-t. Így már páratlan számú háromszög keletkezik. Ekkor azonban a IV. megoldásra gondolva az ott szereplő élsorozat kijelölt ponttól kijelölt pontig menő három-három éle egy A pontból egy B pontba vezet vagy fordítva. Ha tehát páratlan számú élhármasunk van, akkor az csak úgy zárulhat, ha A1-ből B1-be vezet. A szalagot tehát úgy kell zárnunk, hogy a kezdő A1B1 élet a záró B1A1 éllel ragasztjuk össze. Ilyen módon úgynevezett Möbius-szalagot kapunk, amelyiknek csak egy határvonala és egy oldala van. Ilyen síkba hajtogatott szalag 6k+3 háromszögből mindig készíthető, ha k≥1 (13. ábra). 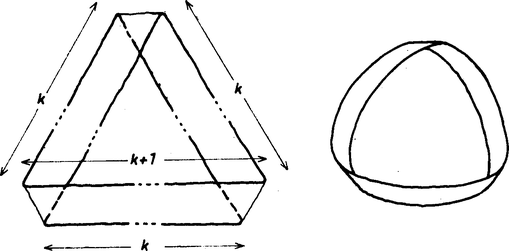 13. ábra
Megjegyzendő, hogy azok a versenyzők, akik akár az 1., akár a 2. megjegyzésben szereplő állítást megfogalmazták, igazolásukra nem tettek kísérletet.
3. Adott n darab, nem feltétlenül különböző egész szám, továbbá két pozitív egész szám p és q. Válasszunk ki az n egész szám közül két egyenlőt, és az egyiket növeljük meg p-vel, a másikból vonjunk le q-t. Ha továbbra is vannak egyenlők az n szám között, akkor ismételjük meg az eljárást. Bizonyítsuk be, hogy véges sok lépés után n különböző számot kapunk.
I. megoldás. Jegyezzük meg először, hogy a számhalmaz legkisebb eleme az eljárás folyamán nem nőhet, a legnagyobb pedig nem csökkenhet. Valóban, a legkisebb elem csak úgy változhat, vagy ha többször szerepel és ezek közül kettőt megváltoztatunk, vagy egy nála nagyobb, többször szereplő szám megváltoztatása során a kisebbített szám átlépi. Mindkét esetben keletkezik egy nála kisebb szám. Hasonló meggondolás érvényes a legnagyobb elemre is.
Vizsgáljuk a legközelebbi egészek közti távolságok változását az eljárás során. Ha egy kétszer szereplő n számot (n-q)-val és (n+p)-vet helyettesítünk, akkor a köztük levő 0 hosszúságú intervallum megszűnik és keletkezik (n-q)-tól a megelőző adott számig, ha van ilyen, egy korábbi intervallumnál nem hosszabb köz: (n-q)-tól a rákövetkezőig egy legfeljebb p+q hosszúságú; (n+p)-től a megelőzőig, ha ez nem n-q, és (n+p)-től a rákövetkezőig, ha van ilyen, egy-egy valamilyen korábbinál nem hosszabb intervallum.
Azt kaptuk tehát, hogy egész számaink közül a szomszédosak közti távolság sohasem nagyobb, mint p+q, vagy valamelyik kezdetbeni távolság.
Ezeket tudva a feladat állítását teljes indukcióval bizonyítjuk. Nyilvánvalóan igaz az állítás, ha 1 vagy 2 egész szám van adva. Tegyük fel, hogy igaz az állítás, ha k darab egész szám adott, és tekintsünk egy k+1 egész számból álló rendszert. A számokat nagyság szerint rendezve, a szomszédosak közti k számú távolság egyike sem nagyobb, semelyik lépés után sem, mint az eredetileg adott számok közti távolságok és p+q közt fellépő legnagyobb érték. Ezt d-vel jelölve a legkisebb és legnagyobb szám közti távolság eszerint nem lépheti túl a kd értéket. Mivel a legkisebb szám nem nő, a legnagyobb nem csökken és egész számokról van szó, ez csak úgy lehetséges, ha bizonyos számú lépés után a legnagyobb szám már nem változik (a legkisebb sem). Innen kezdve azonban elegendő a legnagyobb szám elhagyásával maradó k számot vizsgálni, ezek közt pedig indukciós feltevésünk szerint véges számú lépésben befejeződik az eljárás. Ez a tulajdonság tehát átöröklődik a k+1 egészből álló rendszerre is. Ezzel a bizonyítást befejeztük.
II. megoldás. Ismét használjuk az I. megoldásnak azt a megállapítását, hogy a legkisebb elem nem nő, a legnagyobb nem csökken. Megmutatjuk ezen kívül, hogy ha kerülnek is esetleg számok a változtatás során az eredeti számokat tartalmazó számközön kívül, a számköz hossza nem nőhet n(p+q)-nál többel. Ehhez figyeljük meg, hogy ha a c, c+p+q számközben, a határokat is beleértve, van valamelyik lépés után egy az n szám közül, mondjuk d: akkor d esetleges megváltoztatása esetén vagy d-q≥c és erre c≤d-q≤c+p+q, vagy ha d-q<c, akkor s így erre teljesül a fenti kettős egyenlőtlenség. Így a továbbiak során is mindig lesz legalább egy a számaink közül a c, c+p+q számközben.
Ha az eljárás során egy szám az eredeti számokat tartalmazó számközön kívül kerül, akkor attól legfeljebb p, ill. q távolságra kerülhet, tehát az első p+q hosszúságú intervallumon nem jut túl. Így ha mind az n egész szám kívül kerül is az eredetileg adott számokat tartalmazó számközön (pl. ha eredetileg az összes számok egyenlők voltak), akkor is le- és fölfelé összesen n darab p+q hosszúságú intervallum már biztosan tartalmazni fogja minden lépés után az összes számot.
Hozzárendelünk harmadrészt szám-n-esünkhöz egy olyan függvényt, amelyik minden határon túl nő, ha az eljárás nem fejeződik be, de ezt csak úgy érheti el, ha a számokat tartalmazó számköz is minden határon túl nő. Mivel láttuk, hogy ez nem lehetséges, ezzel bizonyítást nyer állításunk.
Ha p≠q, feltehetjük, hogy p>q, mert ellenkező esetben minden számot az ellentettjével helyettesítve az egyenlők egyikét q-val növelni, a másikat p-vel csökkenteni kell. Legyen a függvényünk ebben az esetben a számok összege. Ez minden lépésben (p-q)-val nő, tehát tetszés szerint nagy lesz, ha megfelelő sokszor ismételjük az eljárást. Ez azonban csak úgy következhetnék be, ha a legnagyobb szám is minden határon túl nőne. A legkisebb viszont nem nőhet, tehát a számainkat tartalmazó számköznek is minden határon túl kellene nőnie, és láttuk, hogy ez nem lehetséges.
Ha p=q, akkor vegyük a számaink közt levő n(n-1)/2 távolság összegét. Két egyenlő számot megváltoztatva csak ezeknek a többiektől való távolsága változik. Egymástól való távolságuk 0-ról 2p-re nő. Ezenkívül, ha az egyenlő számok értéke b, és egy c szám legalább p távolságra van b-től, akkor a változtatás után az egyik számtól való távolság p-vel csökken, a másiktól p-vel nő, összegük tehát nem változik. Ha viszont c a b-től p-nél kisebb távolságra van, akkor a 2|b-c| távolság 2p-re nő (14. ábra). A tekintett összeg tehát minden lépésnél legalább 2p-vel nő. Ez az összeg is csak úgy nőhetne minden határon túl, ha a legkisebb és legnagyobb szám közti távolság is minden határon túl nőne, ez pedig nem lehetséges, mint láttuk. Ezzel a feladat állításának bizonyítását befejeztük.
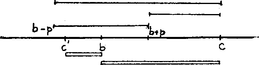 14. ábra
Megjegyzések. 1. Egy versenyző szellemes ötlettel rekurzív eljárást adott meg minden n-re olyan korlát meghatározására, aminél messzebb egyetlen szám sem juthat az eredeti számokat tartalmazó intervallumtól. Eljárása azonban bonyolultabb a fentinél és rosszabb korlátot is eredményez.
2. Az I. megoldásban egy lépésnél hivatkoztunk arra, hogy egész számokról van szó, a II. megoldásból azonban látható, hogy ennek semmi szerepe nincs az állítás helyességében. A megadott függvény mindkét esetben minden határon túl nő, akár egész számokról van szó, akár nem. A feladat állítása tehát igaz, bármilyen n valós szám van adva és bármilyen pozitív szám is p és q.
3. Volt versenyző, aki azt állította, hogy a végül keletkező szám-n-es ugyanaz lesz, akármilyen sorrendben végezzük el az egyenlő párok megváltoztatását, vagy eleve egy általa meghatározott sorrend esetében próbált bizonyítani. Az állítás helyes volta belátható, ha már tudjuk, hogy a feladat állítása igaz. Annak bizonyításához azonban így sem használható fel.
Azt fogjuk bebizonyítani teljes indukcióval, hogy bármilyen sorrendben végezzük is az egyenlő párok megváltoztatását, a végeredmény is, a végzett lépések száma is ugyanaz lesz, mintha először sorra az összes, kezdetben egyenlő számokat változtatjuk meg, majd az ezen változtatások során keletkező összes egyenlő párokat, és így tovább.
Ha van 0 lépésből álló eljárás, ez azt jelenti, hogy csupa különböző szám van adva, tehát más eljárás nem lehetséges, az állítás ebben az esetben igaz. (Ugyanígy egyértelmű az eljárás, és így a végeredmény is, ha van egyetlen lépésben befejeződő eljárás.)
Tegyük fel, hogy igaz a bizonyítandó állítás minden olyan számegyüttes esetére, amelyhez van k-nál kevesebb lépésben befejeződő lépéssorozat. Tekintsünk egy olyan számegyüttest, amelyiknél van egy, k lépésben befejeződő eljárás (k>0). Ha az eljárás azzal kezdődik, hogy először az összes, kezdetben egyenlő párokat változtatjuk meg, akkor a maradó, k-nál kevesebb lépésből álló eljárást helyettesíthetjük azzal az eljárással, amelyben először az összes meglevő, egyenlő számokból álló párt megváltoztatjuk, majd az összes így keletkezett egyenlő párokat és így tovább. Feltevés szerint ezzel a végeredmény nem változik, a lépésszám sem, tehát ugyanez igaz az eredeti eljárásra is.
Ha valamelyik, kezdetben meglevő, egyenlő számokból álló pár megváltoztatása előtt újonnan keletkezett párokat is változtat az eljárás, akkor menjünk el csak addig a lépésig, amelyikben a kérdéses párt változtatjuk meg. Ennek sorra kell kerülnie, mert az eljárás akkor fejeződik be, amikor az összes szám különböző (és tudjuk, hogy ez bekövetkezik). Változtassuk meg először a kérdéses párt, és utána végezzük el az ezen pár megváltoztatása előtti lépéseket. Ezzel az eljárás kérdéses részének az eredményét sem változtattuk meg, a lépések számát sem. Ha még maradt kezdetben egyenlő pár, amit csak újonnan keletkezett párok változtatása után változtattunk meg, azokra alkalmazzuk a leírt változtatást. Így véges számú lépésben az első esetre jutunk vissza anélkül, hogy közben akár az eljárás végeredményén, akár a lépésszámon változtatnánk.
Ezzel beláttuk, hogy az állítás helyessége öröklődik a k-nál kevesebb lépésből álló eljárásokról a k lépésből állókra, s így a bizonyítást befejeztük.
4. A feladattal kapcsolatban felmerül néhány probléma, amelyeknek a tisztázása talán nem lesz túlságosan nehéz. Adott n, p és q esetén maximálisan mennyivel növekedhet meg a számokat tartalmazó számköz hossza? Mi a lépések számának a maximuma? Igaz-e, hogy mindkettő akkor lesz a legnagyobb, ha p=q és az összes számok egyenlők, illetőleg páratlan n esetén egynek az értéke p-vel tér el a többiétől?
|
 PDF | MathML
PDF | MathML