Kezdőlap


Cím:	Fizikai mozgások
Szerző(k):	Simonovits Miklós
Füzet:	1985/január, 9 - 14. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fizikai mozgások ¹

Bevezető

A valóságot gyakran fizikai modellel írjuk le, amit viszont matematikai módszerrel tanulmányozunk. A fizikai modellek sokszor differenciál- vagy differencia-egyenletekre vezetnek. Az utóbbiak tulajdonképpen speciális hátterű rekurziók.^{$^{*}$} Így a fizikai folyamatok számítógépes leírásakor rekurzióval megadott sorozatokkal kell számolnunk. Ebben a fejezetben két fizikai feladatot "oldunk meg'' számítógéppel:
a) leírjuk a lövedék mozgását légellenállás esetén, azaz a ballisztikus görbét;
b) leírjuk a bolygók mozgását a Nap körül.
Azért választottuk éppen ezeket, mert középiskolai megoldásuk igen nehéz. Pontosabban fogalmazva, a Kepler törvények levezethetők középiskolai szakkörökön, de csak nehezen, a ballisztikus görbe középiskolai tárgyalása pedig lényegében értelmetlen lenne. Számítógépes megrajzoltatásuk viszont egyszerű.^{$^{*}$}

Fizikai mozgások leírása differencia-egyenletekkel

Választunk egy alap-időegységet: egy napot, egy órát, egy percet,

...

, és az időt felosztjuk ilyen egységekre:

t = 0

1

2

...

. Csak ezekben az időpillanatokban vizsgáljuk a mozgó pontot. Az erőtörvények alapján kiszámoljuk a gyorsulást, amelyet a síkban két adat jellemez: a vízszintes és függőleges gyorsulás:

A (t)

és

B (t)

. A testet még két adatpár jellemzi: a sebességkoordináták:

U (t)

és

W (t)

, továbbá a helykoordináták:

X (t)

és

Y (t)

.^{$^{*}$} Két időpont között a test mozgását egyenesvonalú egyenletes mozgással közelítjük. Így a következő rekurziókat használjuk:

\begin{matrix} (1) & U (t + h) = U (t) + A (t) \cdot h, \\ (2) & W (t + h) = W (t) + B (t) \cdot h, ahol h = 1. \\ (3) & X (t + h) = X (t) + U (t) \cdot h, \\ (4) & Y (t + h) = Y (t) + W (t) \cdot h . \end{matrix}

Gyakran (3)-ban és (4)-ben

U (t)

és

W (t)

helyett

U (t + 1)

-et és

W (t + 1)

-et használjuk.^{$^{*}$} Ha tehát egy olyan programot írunk, amely kiszámolja az

A (t)

B (t)

gyorsulás-komponenseket a pont helyének és sebességének ismeretében, és ezeket (egyszerűen csak) A, B jelöli, akkor a programunk így néz ki:

(A ferde hajítás esetén például a következő sort használjuk:

\begin{matrix} 1 \emptyset \emptyset A = \emptyset : B = - 9, 81.) \end{matrix}

Az előkészítő lépések után tehát a fenti néhány sor egy végtelen ciklusban kirajzolja a pont pályáját. A

1 \emptyset \emptyset - 12 \emptyset

sorok adják a program "lelkét''. Felhasználjuk, hogy egységnyi időközökben lépünk. A

13 \emptyset

sor arra való, hogy a mozgó pont képét a képernyőn tartsuk. A C konstans megkeresése több módon is történhet, például:
a) periodikus, vagy véges ideig tartó mozgásnál meghatározhatjuk ABS(X) és ABS(Y) időbeli maximumait, és ennek megfelelően kell X-et és Y-t leosztanunk.
b) Megtehetjük, hogy először a

14 \emptyset

sort kiiktatjuk, a

15 \emptyset

helyére pedig PRINT X, Y-t és egy lassító ciklust teszünk be, és úgy futtatjuk le a programot. Így azonnal látjuk, mennyit kell kicsinyítenünk.

Megjegyzés. A valóságos helyzetek leírása bonyolultabb. Figyelnünk kell például a kerekítési hibákra is, illetve az algoritmus hibájára, ami abból adódik, hogy két megfigyelt időpont között a mozgást egyenes vonalú egyenletes mozgással helyettesítjük.

Kepler törvények

Mit akarunk megfigyelni? Azt, hogy
a) a bolygó pályája ellipszis, melynek egyik fókusza a tömegvonzási centrum,
b) a centrumtól távolabb a bolygó mozgása lelassul: azonos időközökben a súrolt terület azonos.

Magyarázat. A program "lelke'' a

7 \emptyset - 8 \emptyset

sor. Ha

r

az origótól vett távolság, akkor

r = \sqrt[]{X^{2}+Y^{2}}

. A

C*(X, Y)=(C*X, C*Y)

vektor az origóból

(X, Y)

-ba mutat és

C*r

hosszúságú. Így az origótól mért távolság négyzetével fordítottan arányos hosszúságú vektor:

\begin{matrix} \frac{C}{r^{3}} * (X, Y)=(\frac{C}{r^{3}}*X, \frac{C}{r^{3}} * Y) \end{matrix}

Hogy gyorsítsuk a számolást,

R=r^{2}

-et használjuk, így kapjuk az

\begin{matrix} A=C*X/R:B=C*Y/R \end{matrix}

gyorsulás koordinátákat.
Ezután a program működése már világos.

5 \emptyset

-ig tart az INPUT egység,

7 \emptyset - 13 \emptyset

a pálya kiszámolása és kirajzolása képvédelemmel, ahogyan azt előzőleg elmagyaráztuk. Ilyen típusú programoknál érdemes az utolsó sorba feljegyezni azokat az adatokat, amelyekkel a program futása biztosított (nem fut ki a kép az ernyőről).

Feladatok

1. Gondoljuk át, mit csinál a

11 \emptyset

-es sor!
2. Keressünk olyan W és C értékeket, hogy a (40,0), (0,W), C indulással a program által kirajzolt görbe a képernyőn maradjon!
3. A bolygó energiája két részből áll: a mozgási energiája

\frac{1}{2} {m v}^{2}

(v^{2}= W^{2}++ U^{2})

, és a potenciális energiája:

- mC/SQR(X^{2} + Y^{2})

.^{$^{*}$} Nyomtassuk ki a teljes energiát

m=1

-re minden lépésben a jobb felső sarokban. Igaznak találjuk-e az energiamegmaradás törvényét?
4. Mit tapasztalunk, ha azt tesszük fel, hogy az erő minden pontban állandó nagyságú, és a centrumba mutató irányú ?
5. Ha C-t negatívnak választjuk (például azonos előjelű elektromos töltéseknél), az taszító erőtérnek felel meg. Ilyenkor hiperbola pályát kapunk. Keressünk megfelelő induló értékeket!
6. Egy párhuzamos fegyverzetű kondenzátor lemezei között egy elektront lövünk keresztül. A lemezek között homogén erőtér hat, mely arányos a fegyverzetekre kapcsolt feszültséggel és merőleges a fegyverzetekre. Írjunk programot, amely bemutatja az elektron mozgását a fegyverzetek között, majd amikor kikerült közülük.
7. Írjunk programot, amely az ingamozgást írja le. Vizsgáljuk meg, mennyire állandó a lengésidő különböző nyílásszögű kilengések esetén! ^{$^{*}$}
8. Készítsük el az "automatikus mozgásábrázolás'' programját: a gép T ideig számolgassa csak a pályát és X, Y maximumát, tegye el az adatokat, majd ebből rajzolja ki a görbe lenormált alakját. T legyen INPUT adat.
9. Ha a bolygómozgás programját többször, különböző adatokkal is kipróbáljuk, észrevehetjük, hogy amikor a bolygó közel kerül a vonzási centrumhoz, akkor a számolási hibák felnövekednek: a bolygó nem egy rögzített ellipszisen fut körbe, hanem egy lassan körbeforduló ellipszisen. Így az alábbi képet kapjuk: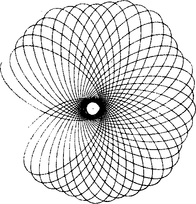

Az ilyen mozgásokat "precesszáló mozgásoknak'' nevezhetnénk. Növeljük meg a fenti induló adatok mellett a pontosságot a DEFDBL A, B, U, W, X, Y, R segítségével. Mit tapasztalunk?

A ballisztikus görbe

Tudjuk, hogy ha eltekintünk a Föld görbületétől és a légellenállástól, akkor egy ágyúgolyó parabola pályát ír le. Ennek a pályának az egyenletét tanuljuk is, így ezzel nem fogunk foglalkozni. Sokkal nehezebb a lövedék mozgását leírni a légellenállás tekintetbevételével ‐ főleg ha még arra is gondolunk, hogy a légellenállás a magassággal változik. Már Newton is foglalkozott a problémával, később Euler dolgozott ki megfelelő közelítő megoldásokat a ballisztikus röppálya leírására. A matematika még jónéhány kiemelkedő alakja tért vissza erre a kérdésre, köztük Clairaut, d'Alembert, Lagrange és Laplace is. A problémát egyebek között az is okozza, hogy a légellenállás csak nagy sebességek esetén közelíthető a sebesség négyzetével arányos erővel.^{$^{*}$} Hogy a probléma nem csak elméletileg érdekes, azt mutatja az is, hogy az I. világháború elején a német tengerészet kikísérletezett egy nagy kaliberű ágyút, amelyről kipróbálásakor derült csak ki, hogy kb. kétszer olyan messze hord, mint gondolták. Ez azon múlt, hogy nagyobb magasságokban a légellenállás kb. feleakkora, mint talajközelben.

Az alábbi program nem igényel túl sok magyarázatot. Feltesszük, hogy a légellenállási lassulás: (A, B) a sebesség négyzetével,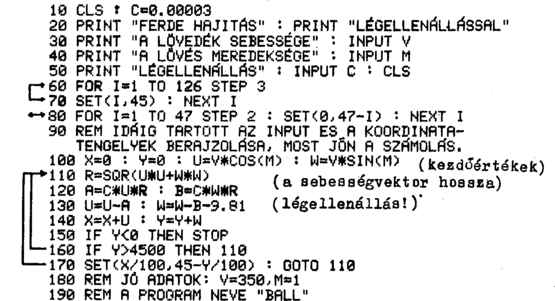

R^{2}=U^{2} +W^{2}

-tel arányos, és az arányossági tényező

C=0,00003

Magyarázat. Az

5 \emptyset

sor kihagyható, hiszen

C

-nek már adtunk értéket a

1 \emptyset

sorban. Így azonban lehetőségünk van a választásra: ha csak NL-t nyomjuk le, marad

C=0,00003

, de ha más adatot akarunk beütni, azt is megtehetjük. A

6 \emptyset - 7 \emptyset

sor az X-tengelyt, a

8 \emptyset

az Y tengelyt nyomtatja.

1 \emptyset \emptyset

adja meg a kiinduló adatokat.

11 \emptyset

és

12 \emptyset

biztosítja, hogy a légellenállás a sebesség négyzetével legyen arányos. Valóban, (U, W) a sebességvektor, R a hossza. Így (

R*U

R*W

) ugyanilyen irányú, de a sebesség négyzetével arányos hosszúságú.

13 \emptyset

-ban a sor végén a gravitációs gyorsulást látjuk.

15 \emptyset

leállítja a programot, mikor a lövedék a földbe csapódik,

16 \emptyset

képvédelem.

Feladatok

1. Módosítsuk a programot úgy, hogy egyetlen koordináta-rendszerben adja meg a lövedék pályáját

C=0

-ra,

C=0,00003

-ra,

C=0,00006

-ra,

C=0,00009

-re és

C=0,00012

-re. Mit tapasztalunk? Lényegesen befolyásolja-e a lövés hatósugarát a légellenállás növekedése?

2. Módosítsuk a fenti programot úgy, hogy
a) a légellenállás

C(Y)=0,00003/Y

legyen: a magassággal fordítottan arányos.
b) C(Y) a talaj mentén

0,00003

legyen,

10000 m

magasságban

0

, és közben lineárisan változzon.
3. Az előző feladat megoldása után még "intézzük el'' azt is, hogy a gép egyszerre rajzolja ki azt a lövedéket, amely konstans

C=0,00003

légellenállás hatására mozog, és azt, amely

0,00003

-től

0

-ig lineárisan csökkenő C(Y) hatása alatt mozog, ahogyan azt az előző feladat b) pontjában leírtuk.
4. Hogyan módosul a lövedék röppályája, ha a légellenállási tényezőt a sebesség

1,71

-edik hatványával vesszük arányosnak a sebesség négyzete helyett? Rajzoltassuk ki mind a két pályát egyszerre!
5. A képernyő közepéről adott sebességgel lövedékeket indítunk különböző irányokba. Rajzoltassuk ki a nyomvonalakat abban az esetben, ha a légellenállástól eltekintünk! A nyomvonalak egy parabola alatti területet töltenek ki, a parabolát burkológörbének nevezzük.

¹Részlet Simonovits Miklós: Számítástechnika c. most készülő tankönyvéből.

^{$^{*}$}A tankönyvben a rekurziók fogalmát egy korábbi fejezet tárgyalja, itt nem ismertetjük azokat. Elég annyit tudnunk, hogy a továbbiakban megadandó (1)‐(4) összefüggések is rekurziók, és hogy a rekurziók különösen alkalmasak számítógépes kezelésre.

^{$^{*}$}Példáink történetileg is nagyon fontosak. Éppen ezek a csillagászati, ballisztikai számítások "követelték ki'' a számítógépet. Megoldásukon a matematika és a fizika legnagyobbjai dolgoztak.

^{$^{*}$}Itt kellemesebb lenne az U és V betűk használata, de V-t már lekötöttük az indulósebességre.

^{$^{*}$}Ha a t időköz elég kicsi, a megfelelő értékek annyira közel esnek egymáshoz, hogy ebben a közelítésben egyenlőnek vehetjük őket.

^{$^{*}$}Ha egy tömegvonzási centrum $c / R^{2}$ erővel vonz egy testet, akkor ahhoz, hogy a testet "kivigyük a végtelenbe'', $c / R$ munkát kell végeznünk (ezt integrálással lehet bizonyítani). Mivel a helyzeti energia csak konstans erejéig van meghatározva, megállapodhatunk abban, hogy azt a végtelenben $0$ -nak vesszük. Ha persze az energia a végtelenben $0$ , akkor (esetünkben) a végesben negatív lesz.

^{$^{*}$}Szokás az inga mozgásának leírásakor a $sin x \approx x$ közelítést használni. Így az ingamozgást harmonikus rezgőmozgással közelíthetjük. Itt most nem ez a célunk. A periódusidőt mérhetjük stopperral is, de írhatunk olyan programot is, amely számolja, hány lépésben érünk egyik végpontból a másikba.

^{$^{*}$}Pólya György "Matematikai módszerek a természettudományban'' című könyvében bővebben ír erről a kérdésről. Megemlíti azt is, hogy a tapasztalattal leginkább az van összhangban, ha a légellenállást $v^{1,71}$ -gyel vesszük arányosnak, ahol $v$ a test sebessége.