|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. Arra kérem az olvasót, vegyen elő papírt, ceruzát és készítsen maga is ábrákat, többfélét is, mint amennyit itt a szöveg mellett lát. Saját tapasztalatai alapján mélyebben beleláthat abba, amiről a következőkben szó lesz.
Rajzoljunk egy kört és bele egy húrnégyszöget, majd húzzuk meg a csúcsaiban a kör érintőit! Húzzuk meg a húrnégyszög és a keletkező érintőnégyszög átlóit (1. ábra).
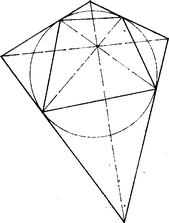 1. ábra
 2. ábra
Készítsünk többféle ábrát is! Most jelöljünk ki 4 pontot a körön úgy, hogy az , pontpár válassza el -t és -t, és legyenek ezekben a pontokban az érintők , , és (2. ábra). Húzzuk meg az , a egyenest, továbbá az és metszéspontját és metszéspontjával összekötő egyenest, végül a és metszéspontját és metszéspontjával összekötő egyenest. Mit sejtünk a húr és érintőnégyszög átlóinak metszéspontjáról?
Négy pont a körön egy konvex és két "hurkolt'' négyszöget határoz meg, és az ezekhez tartozó érintőnégyszögek még aszerint is különbözők lesznek, hogy van-e a körnek olyan félköre, amelyik tartalmazza mind a 4 pontot, vagy nincs. Az ábrák azonban az összes esetben azt sugallják, hogy a húr- és az érintőnégyszög átlóinak a metszéspontja egybeesik. Az, hogy ez mindig így van, könnyen következik a projektív geometria nevezetes eredményeiből.
A "projekció'' szó vetületet jelent, és a projektív geometria valóban olyan geometriai kapcsolatokkal foglalkozik, amelyek vetítésnél sem változnak meg. Ha egy síkot egy másikra vetítünk, párhuzamos vagy egy pontból induló sugarakkal, akkor a síkon levő ábrák rendkívül eltorzulhatnak. Szögek, távolságok, távolságarányok megváltozhatnak, mégis vannak olyan összefüggések, amelyek megmaradnak. Pl. pont vetülete pont, egyenesé egyenes (esetleg egyetlen pont), metszéspont vetülete általában metszéspont stb.
2. Fontos szerepet játszanak a geometria ezen ágában a kúpszeletek. Így nevezik közös néven a hiperbolát, parabolát, ellipszist, kört, sőt hozzájuk véve esetenként még a két egyenesből álló alakzatokat is, mint "elfajult'' kúpszeletet. Ezeknek a vetülete is kúpszelet (elfajulté elfajult).
A kúpszeletekre vonatkozik a következő, Pascaltól, illetőleg Brianchontól származó tételpár.
PASCAL TÉTELE. Ha , , , , , egy kúpszelet pontja, akkor a szemközti oldalpárok metszéspontja egy egyenesen van, azaz az és , a és , továbbá a és egyenesek metszéspontjai. Ha ezek közül egy egyenespár párhuzamos, akkor a további két metszéspontot összekötő egyenes is párhuzamos velük, ha pedig két egyenespár párhuzamos, akkor párhuzamos a harmadik pár egyenes is (3. ábra).
 3. ábra
Brianchon tételében a kúpszelet pontjai helyébe az érintői lépnek, és pont és egyenes szerepe felcserélődik.
BRIANCHON TÉTELE. Ha , , , , , egy kúpszelet érintője, akkor az és metszéspontját és metszéspontjával, a és metszéspontját az és metszéspontjával, végül a és metszéspontját és metszéspontjával összekötő egyenesek egy ponton mennek keresztül (4. ábra).
 4. ábra
Nem fogalmazom meg a tétel kiegészítő részét arra az esetre, ha a felsorolt érintőpárok közül egyesek párhuzamosak.
3. A tételek akkor is érvényesek, ha a felsorolt pontpárok, ill. érintőpárok közül egyesek egybeesnek. Ekkor a pontpár összekötő egyeneseként a pontban húzott érintőt kell venni, egybeeső érintőpár metszéspontjaként pedig az érintési pontot. Ha pl. Pascal tételét 3, egyenként két pontnak számító kúpszeletpontra alkalmazzuk, ill. Brianchon tételét 3 kétszer számító érintőre, akkor a következő tételeket kapjuk:
Egy kúpszeletbe írt háromszög oldalainak a szemközti csúcsban húzott érintővel való metszéspontjai egy egyenesen vannak (5. ábra).
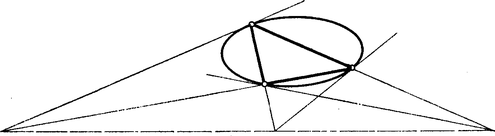 5. ábra
Ha egy háromszög oldalai egy kúpszeletet érintenek, akkor a csúcsokat a szemközti oldalon levő érintési ponttal összekötő egyenesek egy ponton mennek keresztül (6. ábra).
 6. ábra
Igen egyszerű tételeket kaptunk. Próbáljuk meg bebizonyítani abban az esetben, ha a kúpszelet kör (a háromszög köré írt kör, ill. a beírt kör vagy az egyik ún. hozzáírt kör). Bizony nem könnyű!
4. Az 1. pontban megfigyelt összefüggésre Brianchon tételéből következtethetünk, ha azt arra az esetre alkalmazzuk, amelyben egybeesik az és , továbbá a és érintő (7. ábra). Az , , , érintők érintési pontjai legyenek , , , , az és , és , és , és érintők metszéspontja rendre , , , .
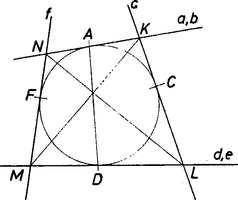 7. ábra
Ekkor a Brianchon tétel azt adja, hogy az , és egyenesek egy ponton mennek keresztül, vagyis a húrnégyszög egyik átlója átmegy az érintőnégyszög átlóinak a metszéspontján. Hasonlóan látható, hogy a húrnégyszög másik átlója is átmegy az érintőnégyszög átlóinak a metszéspontján. A bevezetőben megfigyelt összefüggés tehát bármely kúpszelet húr- és érintőnégyszögére érvényes.
Akiknek esetleg sikerült felkeltenem az érdeklődését a projektív geometria iránt, azok közelebbről megismerkedhetnek vele például Vigassy Lajos: Projektív geometria című középiskolai szakköri füzetéből, amelyik a Tankönyvkiadónál jelent meg 1970-ben.
Várható, hogy az általános tétel kör esetére vonatkozó speciális esete bizonyítható legyen anélkül, hogy túl kellene lépni a középiskolás ismereteken. Az alábbiakban ilyen bizonyításokról lesz szó.
5. A következőt bizonyítjuk tehát be: Legyen , , , egy kör négy pontja; az -ban és -ben, a -ben és -ben, a -ben és -ben, továbbá a -ben és -ban húzott érintők messék egymást sorra a , , , pontokban. Ekkor az , , és egyenesek vagy egy ponton mennek keresztül, vagy párhuzamosak. A tétel Newtontól származik.
 8. ábra
Bizonyítás. Ha és párhuzamos (8. ábra), akkor az ábra szimmetrikus az ezekre az egyenesekre merőleges átmérő egyenesére, így és is merőleges rá, vagyis párhuzamos -vel és -vel. ( itt hurkolt húrnégyszög, és az érintőnégyszög.)
 9. ábra
 10. ábra
Tegyük most fel, hogy és metszi egymást; jelöljük a metszéspontot -vel. A 9. és 10. ábra a pont különböző elhelyezkedései mellett mutatja a viszonyokat. Azt fogjuk belátni, hogy az érintőnégyszög egyik átlója is átmegy -n. Kiindulásul az az észrevétel szolgál, hogy a és érintőszakaszok egyenlők, és könnyen találhatunk ezekkel egyenlő szöget bezáró körsugarakat, tehát ugyancsak egyenlő szakaszokat. Messe -nak az -n túli meghosszabbítása a kört -ben. Az szög az szögre merőleges szárú, és azzal egyező irányú, tehát a két szög egyenlő. Eszerint az és háromszögek hasonlók és egymáshoz képest -kal vannak elforgatva körül.
Most már meg tudunk szerkeszteni egy négyszöghöz hasonló és ahhoz képest -kal elforgatott négyszöget. Ehhez csak merőlegest kell állítani -n át -re, -en át pedig -re.
A keresett merőlegesek közül az utóbbi a egyenes, hiszen ez Thalész tétele szerint valóban merőleges -re. Hasonlóan a keresett -re merőleges egyenest úgy kapjuk meg, hogy -t a kör -vel átellenes pontjával kötjük össze. Jelöljük a két merőleges metszéspontját -fel.
Azt nyertük tehát, hogy az négyszöget körül -kal elforgatva és közben alkalmas arányban nagyítva vagy kicsinyítve, az négyszögbe vihető át. Eközben a átló az szakaszba megy át, tehát merőleges -re.
Ugyanígy szerkeszthetünk meg egy, a -hez hasonló és körül (az előbbivel ellenkező irányban) derékszöggel elforgatott négyszöget. Ennek egyenlő oldalai a és sugarak lesznek, a másik két oldala pedig a -n át, -re, illetve -en át -re merőleges egyenesen fekszik. Ez a két merőleges azonban újra csak a és az egyenes lesz, tehát a négyszög negyedik csúcsa ismét , a keresett négyszög . Ennél a forgatva nyújtásnál tehát az átló ugyancsak -be megy át, vagyis is merőleges -re. Ez azonban azt jelenti, hogy és egy egyenesen van, azaz a egyenes átmegy és metszéspontján, -n. Állításunkat ezzel bebizonyítottuk.
Ugyanígy látható be a és négyszögek alkalmas forgatva nyújtásával, hogy az egyenes is átmegy -n. Ajánljuk az olvasónak, hogy az alaposabb megértés érdekében végezze el a részletes bizonyítást.
6. A bizonyításban sehol sem használtuk ki azt, hogy a pontok milyen sorrendben követik egymást a körön. A két ábrával is azt akartuk hangsúlyozni, hogy ennek nincs szerepe. Ez azt is jelenti, hogy ha rögzítünk pontot a körön, mondjuk az , , , pontokat ebben a sorrendben, akkor azokra több különböző sorrendben is alkalmazhatjuk a kapott eredményt. Az olvasóra hagyom annak az átgondolását, hogy csak lényegesen különböző sorrend adódik, ezek például az , az és az sorrend (11. ábra).
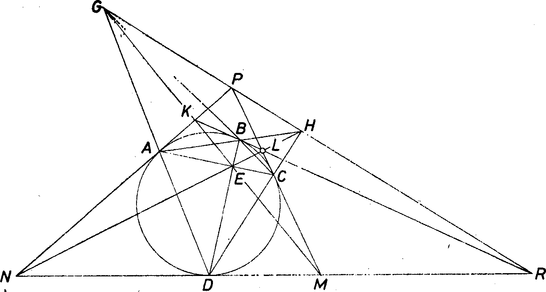 11. ábra
Továbbra is használva az eddigi jelöléseket, az első sorrendnél az adódik, hogy a húr- és az érintőnégyszög átlói, az , , és egyenesek egy ponton keresztül mennek.
A második sorrendnek a 11. ábrán hurkolt húrnégyszög felel meg. Ha az és pontban húzott érintők metszéspontját -vel, a -ben és -ben húzott érintőkét -rel jelöljük, akkor az érintőnégyszög az ábrán a hurkolt négyszög lesz. Az "átlók'' ez esetben az , , illetőleg a és egyenesek. Azt nyerjük tehát, hogy a és a egyenes is átmegy és metszéspontján. Jelöljük ezt -vel.
A harmadik sorrendnél a húrnégyszög ismét hurkolt, csak az eredeti egyszerű négyszög másik szemben fekvő oldalpárja szerepel benne. Az érintőnégyszög viszont az konkáv négyszög. Most tehát azt nyerjük, hogy az , , és egyenesek is egy ponton mennek keresztül. Jelöljük ezt -val.
Az utolsó két eredmény együtt azt adja, ha ismét az és konvex húr-, illetőleg érintőnégyszöget nézzük, hogy az egyikben és a másikban a szemközti oldalpárok metszéspontjai, tehát a , , és pontok egy egyenesen vannak. (Feltéve természetesen, hogy mindegyik metszéspont létrejön. Arra az esetre ismét nem térek ki, ha a szóban forgó egyenespárok közül egyesek párhuzamosak.) Kiegészítésül azt is kaptuk, hogy az érintőnégyszög átlója a húrnégyszög átlóinak metszéspontján kívül az és szemben fekvő oldalak metszéspontján is átmegy, az átló pedig a másik szemben fekvő oldalpár metszéspontján.
7. Térjünk most vissza Pascal említett tételéhez, amely eddig látszólag csak a párhuzam kedvéért szerepelt. Alkalmazzuk ezt arra a hatszögre, amelyik húrnégyszögünkből úgy keletkezik, hogy az és pontot két-két egybeeső és , ill. és pontnak tekintjük. Ekkor a tétel azt adja, hogy az és egyenes metszéspontja ‐ ami itt az -ban, ill. -ben húzott érintő metszéspontját jelenti ‐ az és , azaz és metszéspontja, végül a és metszéspontja egy egyenesen van. Azt kapjuk tehát, hogy a egyenesen van. -t és -t tekintve kétszer számító pontnak, azt kapjuk, hogy is rajta van -n. Így a , , és pont egy egyenesen van. Ezt a tételt is kiadta az előzőekben projektív geometriát nem használó bizonyításunk.
8. Nemrégen értesültem, hogy a bizonyított összefüggésre a múlt évszázadban egy érdekes, a fentitől egészen különböző, a középiskolában szereplőkön túlmenő ismereteket szintén nem igénylő bizonyítást adott Léon Anne. Álljon itt ez a bizonyítás is.
Azt fogjuk bebizonyítani, hogy az érintőnégyszög egy átlóját a húrnégyszög átlói ugyanolyan arányban osztják. A bizonyítást arra az esetre részletezem, amikor egy konvex négyszög oldalszakaszait érinti egy benne levő kör (12. ábra, a 9., 10. ábráénak megfelelő jelöléseket használunk). Legyen és metszéspontja . Ez mindkét szakasznak belső pontja az érintőnégyszög konvex volta miatt.
 12. ábra
Az és háromszög bizonyos oldalait fogjuk összehasonlítani. A két háromszög -nél levő szögei csúcsszögek, tehát egyenlők. Az -nál és -nél levő szögek a kör egy húrjának a két végpontjában húzott érintőkkel alkotott szögei. Az egyenes egy oldalán levő szögek ‐ esetünkben a és szög ‐ egyenlők. Ez következik az szakaszra merőleges átmérőre vonatkozó szimmetriából. Az szög azonban az egyenes ellenkező oldalára esik, s így -ra egészíti ki a szöget.
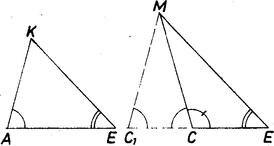 13. ábra
A 13. ábrán újra lerajzoltuk a két háromszöget. Ha pl. a szög nem tompaszög, akkor messük el meghosszabbítását az körüli sugarú körrel, a második metszéspont legyen . (Ha , akkor . ) Ekkor | |
A és háromszög két megfelelő szöge így megegyezik, tehát megfelelő oldalaik aránya egyenlő:
Ugyanilyen meggondolással adódik a és szakaszok metszéspontjára, hogy Azonban és , ill. és egy-egy pontból a körhöz húzott két-két érintőszakasz, tehát egyenlők, így az és pont egyenlő arányú részekre osztja a szakaszt, és mindkettő a szakasz belsejében van. Ez csak úgy lehet, ha egybeesnek. Eszerint , és egy ponton megy keresztül. Ugyanígy látható, hogy , és is egy ponton megy keresztül, tehát mind a négy szakasz egy pontban találkozik. Ezzel beláttuk állításunkat konvex érintőnégyszögre.
Az olvasóra bízom a további (nagy számú) lehetséges eset végigvizsgálását. Minden esetben a fent szereplő háromszögpárokat kell vizsgálni, és azok egyik megfelelő szögpárja két egyenlő szögből fog állni, a másik egymást -ra kiegészítő szögekből, de hol a metszéspontnál, hol a húr végpontjainál lesznek az egyenlő szögek, és az előbbi esetben hol csúcsszögek lesznek, hol közös szárú szögek.
Az elemzés így új gondolatot nem igényel, de annál több figyelmet. Az első bizonyítás annyiban mindenesetre előnyösebb, hogy általános érvényű, ilyen elemző munkát nem igényel.
9. A bizonyítás egy önmagában is érdekes segédtételen alapult. Befejezésül fogalmazzuk meg ezt:
Ha az és háromszög -nál és -nél fekvő szögei egyenlők, a -nél és -nél levő szögek pedig egymást -ra egészítik ki, akkor a és -ből induló megfelelő oldalak aránya megegyezik.
Lásd Nouvelles Annales 1842., 186. o., 1844., 28 és 465. o. |
 PDF | MathML
PDF | MathML