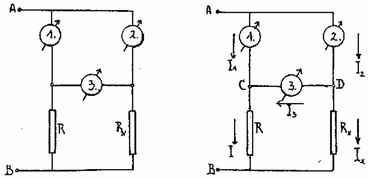Cím:	1984. évi fizika OKTV II. és III. kategóriájának feladatai
Szerző(k):	Vermes Miklós
Füzet:	1984/október, 321 - 326. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. forduló feladatai   1. Egy ismeretlen hosszúságú vízszintes pálya $r$ sugarú félkör alakú pályával folytatódik függőleges síkban (1. ábra). Egy testet megfelelő nagyságú $v$ sebességgel úgy akarunk a pálya elejéről elindítani, hogy az végighaladva a félkörön, ugyanoda érkezzék vissza.Legalább milyen hosszúnak kell lennie a pálya vízszintes részének? A súrlódás elhanyagolható.     1. ábra   (Vermes Miklós)   Megoldás. A tetőponton legalább akkora $v_0$ sebesség szükséges, hogy $m{v}_0^2/r=mg$ alapján a test le ne essék; ez a sebesség $v_0=\sqrt[]{rg}$. A tetőpontról, $2r$ magasságból történő leesés ideje $\sqrt[]{4r/g}$. Ezalatt a $v_0$ sebességgel megtett út $x=v_0\sqrt[]{4r/g}$, $v_0$ értékét felhasználva $x=2r$. Ez a legrövidebb távolság, mert nagyobb $v_0$ esetén messzebb esik le a test. (Az esés ideje ugyanannyi.)   2. Egy fonálingát $45$$°$-os helyzetből elengedünk. Mozgás közben mely helyzetben lesz a legkisebb a gyorsulása? (Vermes Miklós) Megoldás. Az $\alpha$ szöghöz tartozó helyzetben a gyorsulás érintőleges összetevője $g\text{sin}\alpha$, a centrum felé mutató összetevője $v^2/r$ (2. ábra). Az $\alpha$ helyzethez tartozó sebesség az energiamegmaradás törvényével számítható:     2. ábra   Ennek alapján a gyorsulás centrum felé mutató összetevője $2g\left(\text{cos}\alpha -\sqrt[]{2}/2\right)$. A teljes gyorsulás: ${\displaystyle \begin{array}{c}\hfill {\displaystyle a=g\sqrt[]{\text{sin}{}^2\alpha +4{\left(\text{cos}\alpha -\sqrt[]{2}/2\right)}^2}=g\sqrt[]{3\text{cos}{}^2\alpha -4\sqrt[]{2}\text{cos}\alpha +3}\mathrm{.}}\hfill \end{array}}$ A gyorsulás akkor a legkisebb, amikor a gyökjel alatti mennyiség a legkisebb. A gyökjel alatti mennyiség $\text{cos}\alpha$-nak másodfokú függvénye. Mivel $a{x}^2+bx+c$ az $x=-b/2a$ helyen minimális, így a gyorsulás akkor a legkisebb, ha $\begin{array}{c}{\displaystyle \text{cos}{\alpha }_m=\frac{4\sqrt[]{2}}{6}=\frac{2\sqrt[]{2}}{3}=0\mathrm{,}\mathrm{9428,}{\alpha }_m=19\mathrm{,}{47}^{\circ }\mathrm{.}}\end{array}$ Ha az indítási szög $\left({\alpha }_0\right)$ a függőlegestől mérve kisebb vagy egyenlő, mint $\mathrm{41,41}$$°$=arc $\text{cos}$ 0,75, akkora gyorsulás $\alpha =0$ esetén minimális. Vízszintes helyzetből történő indítás esetében a gyorsulás az indításkor a legkisebb. A különböző esetekről áttekintést nyújt a 3. ábra.     3. ábra   3. A fonálon lógó dugattyú tömege $25$ $\text{kg}$ és a héliumgázt tartalmazó hengeres edény tömege szintén $25$ $\text{kg}$ ($4$. ábra). A henger alapterülete $0\mathrm{,}4{\text{dm}}^2$ és a dugattyú távolsága a henger fenekétől $8\mathrm{,}96\text{dm}$. A fonál egy $0\mathrm{,}2$ $\text{m}$ sugarú, $3\text{kg}\cdot {\text{m}}^2$ tehetetlenségi nyomatékú hengerre van felcsévélve. A gázt tartalmazó henger és a dugattyú állandó gyorsulással esnek.     4. ábra   Mennyi a hengerbe zárt héliumgáz tömege? A súrlódás mindenütt elhanyagolható. A külső légköri levegő nyomása $p_0=10{\text{N/cm}}^2$, a hőmérséklet $0{\text{C}}^{\circ }\mathrm{,}g=10{\text{m/s}}^2$. (Vermes Miklós)   Megoldás. Jelöljük a fonálban fellépő erőt $F$-fel! A dugattyú és a henger között semmiféle erőhatás nincs. A hengert a belső $p$ és a külső $p_0$ nyomásokból származó erő mozgatja $a$ gyorsulással (természetesen a gázzal együtt, de a gáz tömegét most elhanyagolhatjuk): $\begin{array}{c}{\displaystyle 25\text{ kg}\cdot a=250\text{ N}-\left(10{\text{ N/cm}}^2-p\right)\cdot 40{\text{ cm}}^2\mathrm{.}}\end{array}$ A dugattyút a súlyból és nyomáskülönbségből származó erő viszi lefelé, a fonálerő húzza felfelé: $\begin{array}{c}{\displaystyle 25\text{kg}\cdot a=250\text{N}+\left(10{\text{N/cm}}^2-p\right)\cdot 40{\text{cm}}^2-F\mathrm{.}}\end{array}$ A csapágyazott hengert az $F$ fonálerő $0\mathrm{,}2\text{m}\cdot F$ forgatónyomatékkal forgatja, a létrejövő szöggyorsulás $a/0\mathrm{,}2\text{m}$, így a forgás törvénye szerint $\begin{array}{c}{\displaystyle 0\mathrm{,}2\text{m}\cdot F=\left(a/0\mathrm{,}2\text{m}\right)\cdot 3\text{kg}\cdot {\text{m}}^2\mathrm{.}}\end{array}$ A háromismeretlenes egyenletrendszer megoldása: $\begin{array}{c}{\displaystyle F=300\text{N}a=4{\text{m/s}}^2\mathrm{,}p=6\mathrm{,}25{\text{N/cm}}^2\mathrm{.}}\end{array}$ Ismerve a hengerbe zárt héliumgáz nyomását és térfogatát $\left(0\mathrm{,}4{\text{dm}}^2\cdot 8\mathrm{,}96\text{dm}=3\mathrm{,}584{\text{dm}}^3\right)$, kiszámíthatjuk a $10{\text{N/cm}}^2$ nyomás melletti $V_0$ normáltérfogatát: $\begin{array}{c}{\displaystyle V_0=\frac{6\mathrm{,}25\left({\text{N/cm}}^2\right)\cdot 3\mathrm{,}584{\text{dm}}^3}{10{\text{N/cm}}^2}=2\mathrm{,}24{\text{dm}}^3}\end{array}$ Ez éppen a moltérfogat tizede, tehát a héliumgáz tömege 0,4 g.   4. Egy vitorláshajó hátszéllel halad a tavon (5. ábra). A szél sebessége $v=10\text{m/s}$. A vitorlára ható közegellenállási erő arányos a sebesség négyzetével; az arányossági tényező $k_1=64\text{N}/{\text{(m/s)}}^2$. A víz alatti részre ható közegellenállási erő szintén arányos a hajó $u$-val jelölt sebességének négyzetével, az arányossági tényező $k_2=4\text{N}/\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>m</mi><mo stretchy="false">/</mo><mi>s</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$. Mennyi a hajó sebessége?     5. ábra   (Lugosi Erzsébet)   Megoldás. A $v-u$ sebességű légáramlat a vitorlát $k_1{\left(v-u\right)}^2$ erővel nyomja. Ez az erő egyenlő a víz alatti részre ható $k_2{u}^2$ közegellenállási erővel: $\begin{array}{c}{\displaystyle k_1{\left(v-u\right)}^2=k_2{u}^2\mathrm{.}}\end{array}$ Rendezve: $\begin{array}{c}{\displaystyle \left(k_1-k_2\right)u^2-2k_{1}vu+k_1{v}^2=0.}\end{array}$ Ennek megoldása: $\begin{array}{c}{\displaystyle u=\frac{k_1/k_2\pm \sqrt[]{k_1/k_2}}{k_1/k_2-1}v\mathrm{.}}\end{array}$ Az első gyök 1,33$v$, a szélnél nagyobb sebességet jelent, így értelmetlen. A második gyök adja meg a helyes eredményt: $u=0\mathrm{,}8v=8\text{m/s}$.   A II. forduló feladatai   1. Egy $r=0\mathrm{,}3\text{m}$ sugarú tömör hengerre papírszalagot csévéltünk, és ennek a végét az $A$ pontban rögzítettük egy $\alpha =36\mathrm{,}{87}^{\circ }$ hajlásszögű lejtőn (6.ábra). A hengert a lejtő végétől $s=0\mathrm{,}16\text{m}$ távolságból elengedjük. Mekkora és milyen irányú a henger középpontjának a sebessége, amikor a henger elhagyja a lejtőt? $g=10{\text{m/s}}^2$.     6. ábra   (Vermes Miklós)   Megoldás. A henger középpontja $c$ sebességgel érkezik a lejtő széléhez (7. ábra). 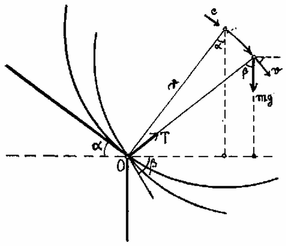    7. ábra   Ez a sebesség az energiamegmaradás törvényével számítható: $\begin{array}{c}{\displaystyle mgs\cdot \text{sin}\alpha =\frac{1}{2}\cdot m{c}^2+\frac{1}{2}\cdot \frac{m{c}^2}{2}=\frac{3m{c}^2}{4}\mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle c=\sqrt[]{\frac{4gs\cdot \text{sin}\alpha }{3}}=1\mathrm{,}131\text{m/s}\mathrm{.}}\end{array}$ Ezután a henger lebillen $O$ körül forogva. Egy bizonyos $\beta$ szögű helyzetben a középpont sebessége legyen $v$, amelynek nagysága ismét az energiamegmaradás törvényével számítható: $\begin{array}{c}{\displaystyle \frac{m{c}^2}{2}+\frac{1}{2}\cdot \frac{m{c}^2}{2}+mgr\left(\text{cos}\alpha -\text{cos}\beta \right)=\frac{m{v}^2}{2}+\frac{1}{2}\cdot \frac{m{v}^2}{2}\mathrm{.}}\end{array}$ Innen $c$ előbbi értékének felhasználásával: A körmozgáshoz szükséges $mr{\omega }^2=m{v}^2/r$ nagyságú erőt a súlyerő $mg\text{cos}\beta$ összetevőjének és a $T$ támaszerőnek a különbsége szolgáltatja: $\begin{array}{c}{\displaystyle \frac{m{v}^2}{r}=mg\text{cos}\beta -T\mathrm{.}}\end{array}$ Az elválás abban a ${\beta }_0$ szögű helyzetben történik, amikor a $T$ támaszerő nulla, vagyis $\begin{array}{c}{\displaystyle mg\text{cos}{\beta }_0=\frac{m{v}^2}{r}\mathrm{.}}\end{array}$ A megcsúszást megakadályozza a papírszalag. Felhasználva $v^2$ értékét: $\begin{array}{c}{\displaystyle g\text{cos}{\beta }_0=\frac{4g\left(s\text{sin}\alpha +r\text{cos}\alpha -r\text{cos}{\beta }_0\right)}{3r}\mathrm{.}}\end{array}$ Innen $\text{cos}{\beta }_0$ (függetlenül $g$-től): $\begin{array}{c}{\displaystyle \text{cos}{\beta }_0=\frac{4g\left(s\text{sin}\alpha +r\text{cos}\alpha \right)}{7r}=0\mathrm{,}\mathrm{64,}{\beta }_0=50\mathrm{,}{21}^{\circ }\mathrm{.}}\end{array}$ A sebesség nagysága: $v_0=\sqrt[]{rg\text{cos}{\beta }_0}=1\mathrm{,}386\text{m/s}$. A sebesség iránya ${\beta }_0=50\mathrm{,}{21}^{\circ }$-kal lefelé irányul a vízszinteshez képest. Ezzel meghatároztuk a sebesség nagyságát és irányát a lejtő elhagyásának pillanatában.   2. Egy $20{\text{cm}}^2$ alapterületű hengerben $7\mathrm{,}2\text{kg}$ tömegű, súrlódásmentes dugattyú zár el $33\text{cm}$ magas, $0{}^{\circ }\text{C}$ hőmérsékletű légoszlopot. A hengerben a dugattyú felett még $7\text{cm}$ magas üres rész van. A külső légnyomás $10{\text{N/cm}}^2$, a higany sűrűsége $13\mathrm{,}6{\text{g/cm}}^3$, a bezárt levegő kezdeti sűrűsége $1\mathrm{,}8{\text{g/dm}}^3$, állandó térfogat melletti fajhője $0\mathrm{,}7\text{J/gK}$, $g=10{\text{m/s}}^2$(8. ábra.)     8. ábra   a) Mekkora az a legnagyobb higanymennyiség, amit a dugattyú fölé tölthetünk (állandó hőmérséklet mellett)?   b) A maximális higanymennyiség betöltése után a levegőt lassan felmelegítjük, amíg az összes higany ki nem csurog. E kísérlet elvégzése közben mennyi hőt kellett a bezárt levegővel közölnünk? (Vermes Miklós)   Megoldás. a) A dugattyú súlya által okozott nyomás $72{\text{N/20 cm}}^2=3\mathrm{,}6{\text{N/cm}}^2$. A levegő térfogata kezdetben $20{\text{cm}}^2\cdot 33\text{cm}=660{\text{cm}}^3$, nyomása $10{\text{N/cm}}^3+3\mathrm{,}6{\text{N/cm}}^2=13\mathrm{,}6{\text{N/cm}}^2$. Ha $x$ magasságú higanyoszlop kerül a dugattyú fölé, akkor a levegő térfogata $\left(33\text{cm}+7\text{cm}-x\right)\cdot 20{\text{cm}}^2$, a levegő nyomása $\left[10{\text{N/cm}}^2+3\mathrm{,}6{\text{N/cm}}^2+0\mathrm{,}136\left({\text{N/cm}}^3\right)\cdot x\right]$. Boyle‐Mariotte törvénye alapján ${\displaystyle \begin{array}{c}\hfill {\displaystyle 13\mathrm{,}6\left({\text{N/cm}}^2\right)\cdot 660{\text{cm}}^3=\left[10{\text{N/cm}}^2+3\mathrm{,}6{\text{N/cm}}^2+0\mathrm{,}136\left({\text{N/cm}}^3\right)\cdot x\right]\cdot (33\text{cm}+}\hfill \\ \hfill {\displaystyle +7\text{cm}-x)\cdot 20{\text{cm}}^2\mathrm{.}}\hfill \end{array}}$ Az egyenlet fizikailag értelmes megoldása $x=10\text{cm}$. Tehát a higany térfogata $200{\text{cm}}^3$, tömege 2720 g. b) Ha ebben a folyamatban a kezdeti és végső állapotot összehasonlítjuk, változatlan nyomás mellett növekedett a levegő térfogata $\left(33\cdot 20\right){\text{cm}}^3$-ről $\left(40\cdot 20\right){\text{cm}}^3$-re. Így az utóbbi állapothoz tartozó hőmérséklet: $\begin{array}{c}{\displaystyle T=\frac{\left(40\cdot 20\right){\text{cm}}^3}{\left(33\cdot 20\right){\text{cm}}^3}\cdot 273\text{K}=331\text{K}\mathrm{,}t=58{}^{\circ }\text{C}\mathrm{.}}\end{array}$ A levegő tömegét megadja kezdeti térfogatának és sűrűségének szorzata: 0,66 dm${}^3\cdot$1,8 g/dm${}^3$ = 1,188 g. A belső energia növeléséhez szükséges hő $\begin{array}{c}{\displaystyle 0\mathrm{,}7\text{J/gK}\cdot 1\mathrm{,}188\text{g}\cdot 58\text{K}=48\mathrm{,}23\text{J}\mathrm{.}}\end{array}$ A melegítés közben a gáz nyomása $\begin{array}{c}{\displaystyle 10{\text{N/cm}}^2+3\mathrm{,}6{\text{N/cm}}^2+0\mathrm{,}136{\text{N/cm}}^3\cdot 10\text{cm}=14\mathrm{,}96{\text{N/cm}}^2}\end{array}$ értékről lineárisan csökken $13\mathrm{,}6{\text{ N/cm}}^2$-re, az átlagos nyomás $14\mathrm{,}28{\text{N/cm}}^2$, a térfogatváltozás $200{\text{cm}}^3$, így a munkavégzés 28,56 J. Hő formájában a belső energia növelésére és a munkavégzés pótlására $48\mathrm{,}23\text{J}+28\mathrm{,}56\text{J}=76\mathrm{,}79\text{J}$ szükséges.   3. A 9. ábrán látható kapcsolásban a három árammérő teljesen egyforma, ellenállása $R_0=2\Omega$. Az $A$ és $B$ pontok között a potenciálkülönbség állandóan $19\text{V}$. Az 1. árammérő $I_1=2\mathrm{,}5\text{A}$-t, a 2. árammérő $I_2=1\mathrm{,}5\t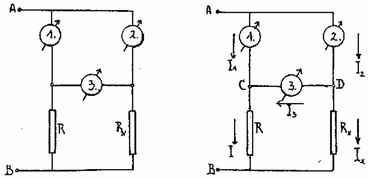ext{A}$-t jelez.     9. ábra   a) Mekkora áramot jelez a 3. árammérő?   b) Vizsgáljuk meg, hogyan változik az $I_3$ áramerősség, ha az $R_x$ ellenállást változtatjuk? (Nagy László)   Megoldás. $a)$ Felírjuk a feszültségesést az $A$ és $C$ pontok között az 1., illetve a 2. és a 3. ampermérőkön keresztül: $\begin{array}{c}{\displaystyle I_1{R}_0=I_2{R}_0+I_3{R}_0\mathrm{,}\text{ innen}}\end{array}$ $\begin{array}{c}{\displaystyle I_3=1\text{A}\mathrm{.}}\end{array}$ $b)$ Az áramelágazás törvénye szerint a $D$ pontban $\begin{array}{c}{\displaystyle I_2=I_2+I_x\mathrm{,}}\end{array}$ a $C$ pontban $\begin{array}{c}{\displaystyle I=I_1+I_3\mathrm{.}}\end{array}$ A feszültségesés $A$ és $C$ között, az 1., illetve a 2. és a 3. ampermérőn keresztül: $\begin{array}{c}{\displaystyle I_1{R}_0=I_2{R}_0+I_3{R}_0\mathrm{.}}\end{array}$ A feszültségesés $D$ és $B$ között, az $R_x$ ellenálláson, illetve az $R$ ellenálláson és a 3. ampermérőn keresztül: $\begin{array}{c}{\displaystyle I_x{R}_x=I_3{R}_0+IR\mathrm{.}}\end{array}$ $R$ értéke az eredeti állapotból meghatározható. Ekkor $AC$ között $R_0{I}_1=5\text{V}$ a feszültség, így $C$ és $B$ között $19\text{V}-5\text{V}=14\text{V}$ a feszültség. Az $R$-en keresztül folyó áramerősség pedig $I_1+I_3=3\mathrm{,}5\text{A}$, tehát $R=14\text{V/3,5}\text{A}=4\Omega$. A teljes 19 V feszültség az ACB úton: $\begin{array}{c}{\displaystyle 19\text{V}=I_1{R}_0+IR\mathrm{.}}\end{array}$ Ezt a kiegyensúlyozatlan Wheatstone-hídra jellemző egyenletrendszert megoldva kapjuk $I_3$ függését $R_x$ től: $\begin{array}{c}{\displaystyle I_3=\frac{19\text{V}\cdot \left(R_x-R\right)}{\left(2R_0+3R\right)R_x+R_0\left(R_0+2R\right)}=\frac{19R_x-76}{16R_x+20}\mathrm{.}}\end{array}$ A függvény grafikonja hiperbola (10. ábra). $R_x=0$-nál $I_3=-3\mathrm{,}8\text{A}$; $R_x=4\Omega$-nál $I_3=0$; $R_x=32\Omega$-nál $I_3=1\text{A}$; $R_x\to \infty$ esetén, $I_3$ értéke 1,1875 A-hez tart. 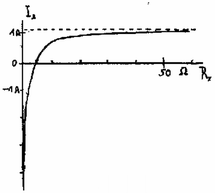    10. ábra   4. Egy 0,5 m sugarú szigetelő anyagból álló, vékonyfalú gömbhéj középpontjában egy kicsiny, pozitív töltésű fémgolyó van, amely a gömbhéj felszínén $+1600\text{<span style="font-weight: normal;font-style: normal;">V</span>}$ potenciált hoz létre. E gömbhéj tetejéről lecsúszik egy 4 kg tömegű kis test, amelynek valamilyen előjelű elektromos töltése van. A lecsúszó test akkor hagyja el a gömböt, amikor sebessége 2 m/s. A súrlódás elhanyagolható, $g=10{\text{m/s}}^2$ . Mekkora a lecsúszó test töltése? (Légrádi Imre)   Megoldás. A lecsúszó test sebességét nem befolyásolja a töltés, mert az elektromos erő merőleges a pályára. Az energiamegmaradás törvényével kiszámítjuk, hogy mely szöghelyzetben hagyta el a kis test a gömböt (11. ábra): 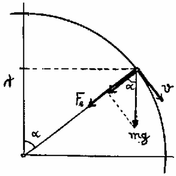    11. ábra   $\begin{array}{c}{\displaystyle \frac{m{v}^2}{2}=mgr\left(1-\text{cos}\alpha \right)\mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle \text{cos}\alpha =1-\frac{v^2}{2gr}=0\mathrm{,}\mathrm{6,}\alpha =53\mathrm{,}{13}^{\circ }\mathrm{.}}\end{array}$ Ebben a helyzetben volt az