Kezdőlap


Cím:	1983. évi Eötvös Loránd Fizikaverseny
Szerző(k):	Károlyházy Frigyes , Nagy László , Vermes Miklós
Füzet:	1984/február, 81 - 85. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat október 29-én rendezte 60. versenyét Budapesten és 11 vidéki városban az abban az évben érettségizettek és középiskolások részére. A versenyzők 5 órai munkaidő alatt oldhatták meg a három feladatot. Bármely segédeszköz használata meg volt engedve, beleértve a zsebszámítógépet is. A versenyen 240 dolgozatot adtak be. Ismertetjük a feladatokat és a verseny eredményét.

1. Egy

L = 1, 528

méter hosszú pálcát vízszintes helyzetből,

h_{1} = 2, 164

méter magasságból elejtünk (1. ábra). Esés közben a pálca baloldali vége rugalmasan ütközik egy

h_{2} = 1, 364

méter magasságban levő szegbe. Az ütközéstől számítva mennyi idő múlva éri el a pálca jobboldali vége a talajt?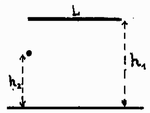

g = 10 {m/s}^{2}

1. ábra

(Vermes Miklós)

Megoldás: Az esés törvénye szerint a szeghez érkezéskor a sebesség: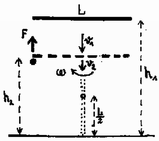

\begin{matrix} v_{1} = \sqrt[]{2 g (h_{1} - h_{2})} = 4 m/s . \end{matrix}

2. ábra

Következik a nem centrális ütközés (2. ábra). A szeghez ütődéskor igen rövid

Δ t

ideig

F

erő ébred. A pálca középpontja egy új

v_{2}

sebességgel megy tovább és

ω

szögsebességgel forogni kezd középpontja körül. Az erőt megadja az impulzus (lendület) időegységre jutó változása:

\begin{matrix} F = \frac{m (v_{1} - v_{2})}{Δ t} . \end{matrix}

A forgás törvénye szerint a forgatónyomaték egyenlő a szöggyorsulás és tehetetlenségi nyomaték szorzatával. A szöggyorsulást

ω / Δ t

adja meg, a közepe körül forgó rúd tehetetlenségi nyomatéka pedig

m L^{2} / 12

\begin{matrix} F \cdot \frac{L}{2} = \frac{ω}{Δ t} \cdot \frac{1}{12} \cdot m L^{2} . \end{matrix}

A két egyenletből

F \cdot Δ t

kiküszöbölésével kapjuk:

\begin{matrix} v_{1} - v_{2} = \frac{ω L}{6} . \end{matrix}

Most figyelembe kell vennünk azt a körülményt, hogy az ütközés rugalmas, tehát a mechanikai energiák összege változatlan marad:

\begin{matrix} \frac{m v_{1}^{2}}{2} = \frac{m v_{2}^{2}}{2} + \frac{ω^{2}}{2} \cdot \frac{1}{12} \cdot m L^{2} . \end{matrix}

Az előző és a mostani egyenletből álló egyenletrendszer megoldása megadja a középpont haladó mozgásának sebességét az ütközés után és a forgás szögsebességét:

\begin{matrix} v_{2} = \frac{v_{1}}{2} = 2 m/s, ω = \frac{3 v_{1}}{L} = 7, 854 s^{- 1} . \end{matrix}

Ezután a pálca tömegközéppontja függőleges lefelé hajítást végez

v_{2}

kezdősebességgel, és állandó

ω

szögsebességgel forog középpontja körül. A legkorábban akkor érheti el a pálca jobboldali vége a talajt, amikor középpontja

L / 2

magasságba ér. A lefelé hajítás útja ekkor

h_{2} - L / 2

. A hajítás úttörvényével:

\begin{matrix} h_{2} - \frac{L}{2} = v_{1} t + \frac{g}{2} \cdot t^{2}, \end{matrix}

számadatainkkal, rendezve:

5 t^{2} + 2 t - 0, 6 = 0

. Ennek megoldása

t = 0, 2 s

. Ez az a legrövidebb időtartam, amelynek végén a pálca jobboldali vége a szeg elhagyása után a talajjal érintkezésbe kerülhet. Ezalatt az elforgás szöge

ω t = 7, 854 \cdot 0, 2 = 1, 57 = 90^{\circ}

. Tehát a pálca épp

0, 2 s

múlva, függőleges helyzetben kerül érintkezésbe a talajjal. A 3. ábra tizedmásodpercenként ábrázolja a pálca helyzetét.

3. ábra

2. Egy csigán átvetett fonál végeire

m_{1} = 8 kg

és

m_{2} = 6 kg

tömegű testeket erősítettünk (4. ábra). A csiga magassága az asztal felett

h = 4

méter, a súrlódás elhanyagolható,

g = 10 {m/s}^{2}

. Az

m_{1}

tömegű testet

α_{0} = 30^{\circ}

-hoz tartozó szöghelyzetből elengedjük.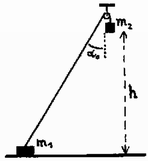

4. ábra

a) Mekkora gyorsulásokkal indulnak el a testek?
b) Mekkorák a testek sebességei és gyorsulásai, amikor az

m_{1}

tömegű test éppen az

m_{2}

tömegű test alatt halad át?
(Nagy László)

Megoldás. Keressük, hogy egy

α

szög által meghatározott helyzetben mekkorák a testek

v_{1}

és

v_{2}

sebességei, valamint

a_{1}

és

a_{2}

gyorsulásai. Az

m_{1}

tömegű test

Δ s

útjához a fonál

Δ s \cdot sin α

rövidülése tartozik, ezért a sebességek összefüggése (5. ábra):

\begin{matrix} v_{2} = v_{1} sin α . \end{matrix}

5. ábra

Az energiamegmaradás törvénye szerint, ha az indítás

α_{0}

fonálhelyzetből történt:

\begin{matrix} m_{2} g (h / cos α_{0} - h / cos α) = \frac{m_{1} v_{1}^{2}}{2} + \frac{m_{2} v_{2}^{2}}{2} . \end{matrix}

Az egyenletrendszer megoldása szolgáltatja a sebességeket:

\begin{matrix} v_{1} = \sqrt[]{\frac{2 m_{2} g h (1 / cos α_{0} - 1 / cos α)}{m_{1} + m_{2} sin^{2} α}}, \\ v_{2} = sin α \sqrt[]{\frac{2 m_{2} g h (1 / cos α_{0} - 1 / cos α)}{m_{1} + m_{2} sin^{2} α}} . \end{matrix}

Az indítás pillanatában természetesen mindkét sebesség nulla. A

0^{\circ}

-os helyzethez tartozóan

v_{20} = 0

és

\begin{matrix} v_{10} = \sqrt[]{2 g h \cdot \frac{m_{2}}{m_{1}} (1 / cos α_{0} - 1)} = 3, 047 m/s . \end{matrix}

A gyorsulások levezetéséhez szükségesek a következő geometriai összefüggések:

\begin{matrix} sin α = \frac{s}{\sqrt[]{s^{2} + h^{2}}}, v_{2} = \frac{s}{\sqrt[]{s^{2} + h^{2}}} \cdot v_{1}, L = \sqrt[]{s^{2} + h^{2}} . \end{matrix}

Differenciáljuk az idő szerint

v_{2}

-t:

\begin{matrix} \frac{d v_{2}}{d t} & = \frac{1}{s^{2} + h^{2}} [\frac{d s}{d t} \sqrt[]{s^{2} + h^{2}} - s \cdot \frac{2 s}{2 \sqrt[]{s^{2} + h^{2}}} \cdot \frac{d s}{d t}] v_{1} + \frac{s}{\sqrt[]{s^{2} + h^{2}}} \cdot \frac{d v_{1}}{d t}, \\ \frac{d v_{2}}{d t} & = \frac{d s}{d t} (\frac{L}{L^{2}} - \frac{s^{2}}{L^{3}}) v_{1} + \frac{s}{L} \cdot \frac{d v_{1}}{d t} . \end{matrix}

Figyelembe véve, hogy

d s / d t = - v_{1}

, valamint tekintettel a geometriai összefüggésekre kapjuk a gyorsulások közti kapcsolatot: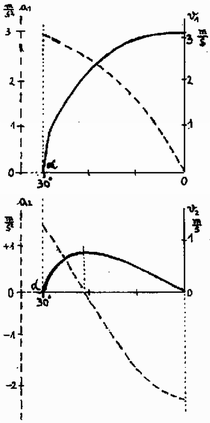

\begin{matrix} a_{2} = - \frac{cos^{3} α}{h} \cdot v_{1}^{2} + a_{1} sin α . \end{matrix}

Szükségünk van a fonálerőre is. Ez

m_{1}

tömeg esetében

F sin α = m_{1} a_{1}

, az

m_{2}

tömeg esetében

F = m_{2} (g - a_{2})

. A fonálerőket egyenlővé téve:

\begin{matrix} m_{1} a_{1} + m_{2} a_{2} sin α = m_{2} g sin α . \end{matrix}

A legutóbbi két egyenletünkből álló egyenletrendszert megoldva megkapjuk a gyorsulásokat. Felhasználva

v_{1}

és

v_{2}

előbb kiszámított értékeit is, az eredmények:

\begin{matrix} a_{1} & = \frac{m_{2} g sin α}{{(m_{1} + m_{2} sin^{2} α)}^{2}} \cdot [(m_{1} + m_{2} sin^{2} α) + 2 m_{2} cos^{3} α (1 / cos α_{0} - 1 / cos α)], \\ a_{2} & = \frac{m_{2} g}{{(m_{1} + m_{2} sin^{2} α)}^{2}} [(m_{1} + m_{2} sin^{2} α) sin^{2} α - 2 m_{1} cos^{3} α (1 / cos α_{0} - 1 / cos α)] . \end{matrix}

Az indulás pillanatában a gyorsulások:

\begin{matrix} a_{1 i} & = g \cdot \frac{m_{2} sin α_{0}}{m_{1} + m_{2} sin^{2} α_{0}} = 3, 158 {m/s}^{2}, \\ a_{2 i} & = g \cdot \frac{m_{2} sin^{2} α_{0}}{m_{1} + m_{2} sin^{2} α_{0}} = 1, 579 {m/s}^{2} . \end{matrix}

α = 0^{\circ}

-hoz tartozó gyorsulások:

\begin{matrix} a_{10} = 0, a_{20} = - g \cdot \frac{2 m_{2}}{m_{1}} (1 / cos α_{0} - 1) = - 2, 321 {m/s}^{2} . \end{matrix}

A 6. ábra a sebességek és gyorsulások

α

szögtől való függését mutatja.

6. ábra

Ha csak a feladott kérdésekben szereplő speciális értékekre van szükség, akkor sokkal rövidebben járhatunk el úgy, hogy egyenleteinkben már kezdettől fogva

α_{0} = 30^{\circ}

, illetve

0^{\circ}

-ot használunk.
Speciális közelítő eljárások is vannak

α_{20}

kiszámítására (7. ábra). Lássunk ezek közül kettőt!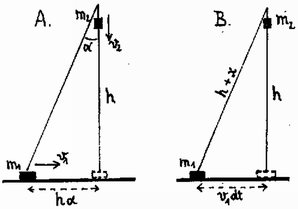

7. ábra

A. A fonál

ω

szögsebességgel közeledik a függőleges helyzethez. Az

m_{1}

tömegű test utolsó útdarabja egyrészt

h α

, másrészt

ω d t \cdot h

h α = ω d t \cdot h

, vagyis

d t = α / ω

. Ezalatt csökken a sebesség

v_{1} sin α

-ról 0-ra, tehát a sebességváltozás

d v_{2} = - v_{1} sin α

. A keresett gyorsulás:

\begin{matrix} a_{20} = \frac{d v_{2}}{d t} = \frac{- v_{1} sin α}{α / ω} = - \frac{v_{1}^{2}}{h} \cdot \frac{sin α}{α} = - \frac{v_{1}^{2}}{h} . \end{matrix}

B. A függőleges fonálhelyzethez közel, amikor az

m_{1}

tömegű test egyenletesen mozog

v_{1}

sebességgel, Pitagorasz‐tétellel:

\begin{matrix} {(h + x)}^{2} = h^{2} + {(v_{1} d t)}^{2}, ebből x = \frac{v_{1}^{2} {(d t)}^{2}}{2 h} . \end{matrix}

m_{2}

tömegű test közelítően egyenletesen lassulva mozog a megállásig, ezért

x = - a_{20} {(d t)}^{2} / 2

. A két

x

-re kapott értéket egyenlővé téve

a_{20} = - v_{1}^{2} / h

3. A világűrben elektromosan semleges, belül üres, zárt vezető gömbhéj lebeg. Közepében kicsiny, pozitív töltésű fémgolyó nyugszik szabadon. Távoli kondenzátorlemezek segítségével a gömb alakú "Faraday-kalitka'' körül homogén elektromos teret hozunk létre. Mozgásba jön-e a kicsiny fémgolyó, illetőleg a gömbhéj és ha igen, miképpen?
(Károlyházy Frigyes)

Megoldás. A külső tér nélkül a kis fémgolyó a gömbhéj középpontjában (labilis) egyensúlyi helyzetben van (8. a ábra).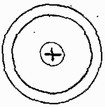

8. a ábra

A külső tér létrehozásának pillanatában a gömbhéjon megosztott töltések mutatkoznak. Így a kis fémgolyót a gömbhéj árnyékoló hatásával védi a külső tértől. Ezért a külső tér bekapcsolásának pillanatában a kis fémgolyó gyorsulása még nulla. A gömbhéjnak az ábra szerinti bal oldalán a fémgolyó által létrehozott tér és a külső tér ellentétes irányú, a jobb oldalon pedig azonos irányú. A gömbhéjon a töltésmegosztásból származó negatív töltésekre ható eredő erő ezért kisebb lesz, mint a pozitív töltésekre ható eredő erő. A gömbhéj ezért a külső tér bekapcsolásának pillanatában jobbra indul el.(8. b ábra). Amikor a gömbhéj már elmozdult, a fémgolyó már nem lesz a középpontban. Ekkor a fémgolyón levő pozitív töltés is töltésmegosztást hoz létre a gömbhéjon. E töltések hatására a fémgolyó a hozzá közelebb eső oldalon levő negatív töltések irányába, tehát balra indul el (8. c ábra). Amint a golyó és a gömbhéj összeér, az egész fémtárgy pozitív töltésű lesz, és a tér által megszabott irányban (az ábra szerint jobbra) gyorsulva mozog (8. d ábra).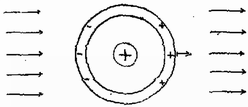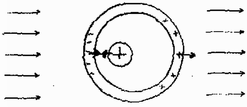

8. b ábra

8. c ábra

8. d ábra

A verseny eredménye

I. díjat ketten kaptak egyenlő helyezésben: Árkossy Ottó, a budapesti Semmelweis Orvostudományi Egyetem hallgatója, aki Esztergomban a Dobó Katalin Gimnáziumban érettségizett mint Sipos Imre tanítványa és Erdős László a budapesti Berzsenyi Dániel Gimnázium IV. o. tanulója, tanára Koltai Mária.

II. díjat kapott Fodor Gyula, a budapesti Móricz Zsigmond Gimnázium IV. o. tanulója, tanára Tarnócziné Gedeon Melitta.

III. díjat ketten kaptak egyenlő helyezésben: Csillag Péter, a budapesti Landler Jenő Gépészeti és Híradástechnikai Szakközépiskola IV. o. tanulója és Frei Zsolt, a budapesti Eötvös Loránd Tudományegyetem Természettudományi Karának fizikus hallgatója, aki Pécsett a Nagy Lajos Gimnáziumban érettségizett mint Kállai Miklósné és Tornyos Tivadar tanítványa.
Dicséretet hárman kaptak egyenlő helyezésben: Kovács Tamás, a debreceni Kossuth Lajos Gimnázium IV. o. tanulója, tanára Szegedi Ervin, továbbá Náray Miklós honvéd, aki Budapesten érettségizett az I. István Gimnáziumban mint Moór Ágnes tanítványa és Sczigel Gábor honvéd, aki Budapesten az Apáczai Csere János Gimnáziumban érettségizett, mint Holics László tanítványa.
Az 1. feladatot a felsoroltakon kívül teljesen megoldották még a következő versenyzők: Drobni András (Bp. I. István G. IV. o. t.: Cseh Géza), Mandzsu Zoltán (Bp. Fazekas M. G. IV. o. t.: Horváth Gábor), Rácz Attila (Sopron, Berzsenyi D. G. IV. o. t.: Nagy Márton), Szakállas Gyula (Zalaegerszeg, Zrínyi M. G. IV. o. t.: Gódor Győzőné), Törőcsik Jenő honvéd (érettségizett Bp. Fazekas M. G. t.: Horváth Gábor).
A 2. feladatot a nyerteseken kívül teljesen megoldották még a következő versenyzők: Beke Sándor honvéd (érettségizett Miskolc, Földes F. G. t.: Zámborszky Ferenc), Fáth Gábor (Bp. Fazekas M. G. IV. o. t.: Horváth Gábor), Gaál Péter (Bp. Apáczai Cs. J. G. o. t.: Zsigri Ferenc), Megyesi Gábor (Szeged, Ságvári E. G. III. o. t.: Juhászné Mészáros Mária), Pfeil Tamás (Dunaújváros, Münnich F. G. III. o. t.: Székelyi Sándorné).