| Cím: | Ki miben tudós? - matematikai vetélkedő | ||
| Szerző(k): | Reiman István | ||
| Füzet: | 1984/május, 199 - 206. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Egyéb (KöMaL pontverseny is) | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A Magyar Televízió első ízben 1964-ben rendezte meg a ,,Ki miben tudós?'' vetélkedőt matematikából: Azóta 1966-ban, 1968-ban, majd hosszabb szünet után 1984-ben került sor ismét a nyilvános vetélkedőre.  Az elődöntőből 4-en minden párból a több pontot elérő versenyző jutott tovább a középdöntőbe. Végül a középdöntő két győztese vetélkedett az első és második helyért.  Megyesi Gábor és Erdős László Az elő-; közép- és döntők során minden versenyzőpárnak 4‐4 feladatot kellett megoldania. Egy feladat megoldására perc gondolkodási idő és a megoldás elmondására legfeljebb perc jutott. A verseny első helyezettje Megyesi Gábor (Szeged, Ságvári E. Gyak. Gimn., III. o. t.) a második Erdős László (Budapest, Berzsenyi D. Gimn., IV. o. t.). Olvasóink közül is bizonyára sokan izgulták végig a versenyt a televízió képernyői előtt, esetleg maguk is megpróbálták a feladatokat megoldani. Sokszor talán úgy érezték, hogy a perc gondolkodási idő még a feladat megértésére sem elegendő. Valóban, ez a verseny nemcsak azt kívánta a versenyzőktől, hogy jó gyakorlatuk legyen feladatmegoldásban, széles körű matematikai ismeretekkel rendelkezzenek, hanem azt is, hogy igen gyorsan ,,kapcsoljanak'', és képesek legyenek röviden megfogalmazni a megoldásokat.  A diákok teljesítményét háromtagú zsűri bírálta el: Császár Ákos akadémikus (elnök), Lovász László akadémikus és Pelikán József egy. adjunktus (a két utóbbi maga is Ki miben tudós? verseny győztese volt). A feladatokat egy bizottság állította össze, és a kérdéseket Reiman István egy. docens tette fel. A területi (megyei, fővárosi) versenyek írásbeli feladatai 1. Legyenek és 1-től különböző pozitív valós számok ! Tudjuk, hogy minden valós -re 2. Oldjuk meg a 3. Négy egységsugarú gömb mindegyike érinti a többi hármat. Mekkora annak a gömbnek a sugara, amely érinti mind a négy előbbi gömböt és közülük egyiket sem tartalmazza a belsejében ? 4. Van-e megoldása a pozitív egészek körében a 5. Egy háromszög oldalainak hossza legyen , szögfelezőinek hossza pedig . Bizonyítsuk be, hogy 6. Adott a síkon véges sok piros pont és véges sok fekete pont úgy, hogy semelyik három nincs egy egyenesen, és bármely négy pont közül a pirosak elválaszthatók egy egyenessel a feketéktől. Bizonyítsuk be, hogy van olyan egyenes a síkon, amely az összes piros pontot elválasztja az összes fekete ponttól ! 7. Hány olyan téglatest van (az egybevágókat azonosnak tekintve), amelynek legkisebb éle egységnyi hosszúságú, további élhosszúságai és testátlójának hossza egy mértani sorozat négy egymást követő eleme ? 8. Bizonyítandó, hogy ha minden valós Az országos döntő írásbeli feladatai 1. Bizonyítsuk be, hogy ha pozitív egész és nem negatív egész, akkor 2. Hányféle sorrendben érhet célba öt futó, ha közöttük holtversenyek is lehetségesek ? 3. Egy körbe írt konvex tizenkétszög hat oldalának hossza , hat oldaláé pedig . Mekkora a tizenkétszög köré írt kör sugara ? 4. Egy tagú társaságban mindenki legfeljebb négy másikat ismer. Bizonyítsuk be, hogy van a társaságban öt ember, akik közül egyik sem ismeri a másikat. 5. Egy számsorozat -adik eleme 6. Legyen egy pozitív egészekből álló mértani sorozat első eleme, a sorozat hányadosa -nél nagyobb egész szám. Bizonyítsuk be, hogy nem létezik olyan különböző számokból álló mértani sorozat, amelyben az első elem mindegyike két különböző -beli elem összege. Az országos döntő szóbeli részének a feladatai 1. Van-e az 2. Az és a sík egybevágó szabályos háromszögei. Milyen ponthármast alkotnak az szakaszok felezőpontjai ? 3. Állapítsuk meg az 4. Bizonyítsuk be, hogy egy tetraéder bármely belső pontjából legalább egy él tompaszög alatt látszik. 5. Elhelyezhető-e hét egyenes a síkon úgy, hogy legalább hat metszésponton három egyenes haladjon át, legalább négy pontban pedig két egyenes messe egymást ? 6. Hányféleképpen lehet a kocka lapjait piros és kék színnel kiszínezni, ha nem tekintünk különbözőnek két olyan színezést, amelyek a kocka alkalmas elforgatásával egymásba átvihetők ? (Minden lap vagy piros vagy kék színű; mindegyik szín előfordul legalább egyszer.) 7. Egy 2 élhosszúságú szabályos tetraédert megpörgetünk egyik éle körül. Mekkora a tetraéder által súrolt térrész térfogata ? 8. Legyen -nél nagyobb pozitív egész. Bizonyítsuk be, hogy 9. Egy négyzetrács két rácspontját összekötjük egy egyenessel. Bizonyítsuk be, hogy megadható olyan pozitív szám, amelyre igaz, hogy minden rácspont, amely nincs az egyenesen, az egyenestől -nél nagyobb távolságra van. 10. Adjunk meg olyan szakaszokat, amelyek az alábbi derékszögű háromszög kerületén levő pontokat kötnek össze, és a háromszög minden belső- és határpontja pontosan egy szakaszhoz tartozik hozzá. (A szakaszok zártak.) 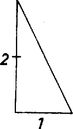 11. Kornél két egyforma nagyságú korongot talált, mindkét korong oldalpalástja egyforma részre van felosztva. Mindkét korongon rész sárgára, pedig zöldre van festve. Egymásra helyezhetők-e a korongok úgy, hogy az oldalpalást osztóvonalai a két korongnál egy egyenesbe essenek, és az egymás fölé kerülő oldalrészek legalább esetben azonos színűek legyenek?  12. Léteznek-e olyan egész számok, amelyek kielégítik az Az elődöntők feladatai 1. Egy társasjátékban az, aki először hibázik, 10 fillért fizet a kasszába, majd minden további hibázó a kasszában éppen levő összeg kétszeresét. Mennyit fizet az, aki nyolcadszorra hibázik? 2. A pont az hegyesszögű háromszög olyan belső pontja, amelynek az és oldalakra vonatkozó tükörképe a háromszög köré írt körön van. Mindig igaz-e, hogy -nek a oldalra vonatkozó tükörképe is a körön van? 3. Egy 5 elemű halmaznak legfeljebb hány részhalmazát lehet megadni úgy, hogy bármely kettőnek legyen közös eleme? 4. Egy klubesten lány és fiú vett részt. Egy játék során mindenki felírta egy cédulára, hogy az est folyamán hány különböző partnerrel táncolt. A cédulákon rendre a Bizonyítsuk be, hogy valaki tévedett. 1. Melyek azok a prímszámok, amelyekre négyzetszám ? 2. Mutassuk meg, hogy egy konvex ötszög oldalainak összhossza mindig kisebb az átlók összhosszánál. 3. Legyen -nél kisebb pozitív szám. Bizonyítsuk be, hogy 4. Legfeljebb hány huszár helyezhető el a sakktáblán úgy, hogy egyik se üsse a másikat? 1. Az természetes számokat be akarjuk osztani valahány osztályba úgy, hogy egyik osztályban se forduljon elő egy számmal együtt a kétszerese is. Legalább hány osztályra van szükség? 2. Egy kocka minden csúcsából vektort indítunk a szemközti csúcsból kiinduló három él felezőpontjába. Bizonyítsuk be, hogy az így kapott vektor összege . (Egy csúccsal szemközti a tőle legtávolabb eső csúcs.) 3. valós szám közül bármelyik összege nagyobb a többi szám összegénél. Bizonyítsuk be, hogy mindegyik szám pozitív. 4. Kovács úr elégedetten nézegeti a tapétát a falon. Éppen most fejezte be szokásos ellenőrző körútját, amelynek során minden ajtón pontosan egyszer halad át. Hol van most? 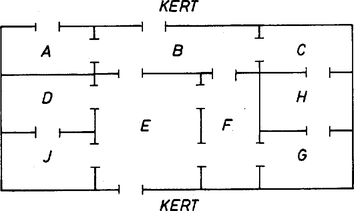 1. Tizenhat ember pénzt tesz egy dobozba. Az első egy forintot tesz be és minden következő kétszer annyit, mint az előző. Bizonyítsuk be, hogy az összegyűlt forintok száma osztható -tel és -tel. 2. Bizonyítsuk be, hogy minden olyan szabályos sokszög, amelynek kerülete és területe számértékben megegyezik, lefedhető egy legfeljebb egység sugarú körrel. 3. András és Béla a következő játékot játsszák: Egy papíron számú mínusz jel van egy sorban. Aki lépésre következik, egy mínuszt pluszra változtathat, vagy két, közvetlenül egymás mellett álló mínuszt pluszra változtathat. András kezd, majd felváltva lépnek, és az nyer, aki az utolsó mínuszt változtatja pluszra. Feltéve, hogy mind a ketten a legjobban játszanak, ki nyer ? András vagy Béla ? 4. Egy kilenc soros és tíz oszlopos táblázat első oszlopának első helyén az egyes, az első oszlop utolsó helyén pedig a kilencvenes szám áll. Beírható-e a táblázatba az összes és közötti egész szám úgy, hogy szomszédos számok csak egymás mellé vagy egymás alá kerüljenek ? A középdöntő feladatai 1. Bizonyítsuk be, hogy háromjegyű szám közül mindig kiválasztható kettő úgy, hogy egymás mellé írva őket, a kapott hatjegyű szám osztható -tel. 2. Egy könyvespolcon könyv van egymás mellett. Egy ,,lépésen'' azt értjük, hogy két szomszédos könyvet felcserélünk (a többit változatlanul hagyjuk). Minimálisan hány lépéssel érhető el az, hogy a két szélső könyv helyet cseréljen? 3. Az ábrán látható három egységsugarú kör középpontja . János és József azon vitatkoznak, hogy a három kör közös részének (a vonalkázott résznek) a területe nagyobb vagy kisebb egy kör területének a negyedrészénél! Döntsük el a vitát!  4. Van egy ,,három karú mérlegünk''. Ez csak azt tudja jelezni, hogy a három serpenyőjében egyforma súly van-e vagy sem. pénzdarabunk közül az egyik hamis (más súlyú, mint a többiek). Hány méréssel lehet biztosan kiválasztani a hamisat, ha ? És ha ? 1. Mutassuk meg, hogy bármely konvex sokszögnek van két olyan csúcsa, amelyek összekötő szakasza a többi csúcsból legalább -os szög alatt látszik. 2. Az expedíció útra készen áll, néhány csomagot azonban még el kellene helyezniük az útiládákban. Sokat bajlódnak, mert a parancsnok nem engedi, hogy az előző napokban ládákba rakott dolgokhoz hozzányúljanak. A próbálkozások során kiderül, hogy bármely csomag bármely ládában elfér egy láda kivételével; továbbá bármely ládában elhelyezhető valamelyik csomag. Sikerült-e minden csomagot magukkal vinniük, ha a ládák és a csomagok száma egyenlő ? 3. Egy legalább fős munkahelyen bármely két ember vagy jóban vagy rosszban van egymással, vagy pedig nem ismeri egymást, és minden eset elő is fordul. Bizonyítsuk be, hogy van négy ember, akik között már mindhárom viszony előfordul. 4. Egy háromszöget szétvágunk kisebb háromszögekre úgy, hogy a kis háromszögek egyetlen csúcsa se essék a másik kis háromszög vagy az eredeti háromszög oldalának belső pontjára. Lehetséges-e, hogy így háromszöget kapjunk ? A döntő feladatai 1. A tapasztalat szerint egy adott időszakban fiú és leány születésének a valószínűsége nem teljesen egyforma. Azoknál a két gyermekes családoknál, akiknek a gyermekei ebben az időszakban születtek, mi a valószínűbb: egynemű vagy különböző nemű testvérpár ? (Ikerszüléseket nem veszünk figyelembe.) 2. Valaki úgy vélekedik, hogy az hoz szerencsét, ha lottószelvényét ,,összevissza'' tölti ki. Ezen azt érti, hogy ne forduljon elő, hogy egy megjelölt szám után valamikor később egy nagyobbat és azután valamikor egy még nagyobbat jelöl meg, sem pedig az, hogy egy megjelölt szám után később egy kisebbet és még később egy még kisebbet jelöl meg. Bizonyítsuk be, hogy lehetetlen így kitölteni egy lottószelvényt. 3. Egy kukac talált egy milliméter sugarú, tökéletesen gömb alakú almát. Azonnal belerágta magát, majd milliméteres út megtétele után jóllakottan távozott belőle. Két egyenlő részre lehet-e vágni egy vágással az almát, úgy, hogy az egyik fél almában ne legyen nyoma a kukacnak ? 4. Egy asztalon egy sorban tányér van. Ubul mindkét kezével megragad egy-egy tetszőleges tányért a hat közül, és mindkettőt egy hellyel jobbra vagy balra odébb helyezi (ha már van ott tányér, akkor annak a tetejére). Ezt ismételve el tudja-e érni, hogy az összes tányér egy oszlopba kerüljön ? |