| Cím: | 1983. évi Kürschák József matematikai tanulóverseny feladatainak megoldása | ||
| Szerző(k): | Surányi János | ||
| Füzet: | 1984/február, 51 - 60. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Kürschák József (korábban Eötvös Loránd) | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. Bizonyítsuk be, hogy ha az , , racionális számokra I. megoldás. Az értékhármas nyilvánvalóan megoldása az egyenletnek. Ha van ettől különböző megoldás, ahhoz található olyan, -tól különböző racionális szám, amelyikre
Válasszunk egy olyan egész számokból álló megoldást, amelyikre a lehető legkisebb. Ilyen van, mert egy megoldáshoz összesen csak véges sok olyan, egész számokból álló hármas van, amelyikre az abszolút értékek összege nem nagyobb, mint az adott megoldásban. Ezek közül tartsuk meg azokat, amelyeket , , ill. helyébe helyettesítve (1) teljesül. Ezek közül kiválasztható egy olyan hármas, amelyikben az abszolút értékek összege minimális. Ha ebben a megoldásban , akkor Ha , akkor Megjegyzések. 1. Többen abból az észrevételből indultak ki, hogy 2. Az I. megoldáshoz hasonló utat követő versenyzők vagy azt bizonyították, hogy -nek, -nak és -nek 3 akármilyen magas hatványával oszthatónak kell lennie, és ez 0-tól különböző egész számra nem lehetséges, vagy belátták, hogy egy, az -tól különböző megoldásról feltehető, hogy relatív prím számokból áll, viszont másrészről mindegyiknek oszthatónak kellene lennie 3-mal, ilyen megoldás tehát nem létezik. Csak kevesen hivatkoztak a törzsszámhatványokra történő felbontás egyértelműségére, de ennek hiányát a bizottság nem tekintette hibának. 3. A bizonyítás egy érdekes befejezése volt a következő: Ha 3 kitevője , és felbontásában , , ill. , akkor (1) egymás utáni tagjaiban 3 kitevője Ez a meggondolás felhívja a figyelmet arra, hogy az állítás az II. megoldás. Ismeretes és könnyen igazolható a következő azonosság-pár: Az utolsó tényező csak úgy lehet 0, ha benne mind a 3 tag 0, tehát többek közt Marad még az a lehetőség, hogy
A két egyenletből küszöböljük ki a tartalmazó tagokat, az első egyenlet bal oldalának -szorosából a másodikénak -szeresét levonva: Megjegyzés. Ugyanígy látható, hogy ha olyan racionális szám, amelyik nem köbe racionális számnak, akkor az 2. feladat. Az polinom együtthatói nem negatívak és az egyenletnek valós gyöke van. Bizonyítsuk be, hogy . I. megoldás. A polinomnak valós 0-helye csak negatív szám lehet, mert nem negatív helyen egy tag sem negatív és az állandó tag 1, és így Feltétel szerint valós gyök van, jelöljük ezeket -nel. Itt tehát az -k pozitív számok. Az egyenlet gyökei és együtthatói közti összefüggések szerint -re
Alkalmazzuk az összegre a számtani és mértani közép közti egyenlőtlenséget. A tagok szorzatában minden , szerepelni fog, éspedig ugyanazon az hatványon ( ahányféleképpen a maradó gyök közül -et kiválaszthatunk mellé, azaz , tehát ez a szorzat, felhasználva (1)-et Ezt minden együtthatóra alkalmazva, azt kapjuk, hogy Megjegyzés. A megoldás azt is adja, hogy ha nem negatív szám, akkor II. megoldás. Ismeretes, hogy ha egy Megjegyzés. Ez az eljárás az előző megoldáshoz fűzött megjegyzés általánosítását közvetlenül csak pozitív egész -re adja. Érvényes azonban a felhasznált egyenlőtlenség következő általánosítása, ún. súlyozott alakja: Ha és pozitív számok(súlyok), és , pozitív számok, akkor
A (2) alatti egyenlőtlenség ‐ és általánosítása is ‐ racionális súlyok esetén egyszerűen visszavezethető a súlyok nélküli egyenlőtlenségre; ha pedig a súlyok közt van irracionális szám is, akkor a bizonyítás úgy történik, hogy az irracionális súlyokat megközelítjük racionális számokkal, és vizsgáljuk, mi történik, ha a megközelítést minden határon túl finomítjuk. III. megoldás. Általánosan azt bizonyítjuk, hogy tetszés szerinti pozitív -re Ha az -k közt vannak különbözők, akkor van 1-nél kisebb is, nagyobb is. A számok sorrendjét megváltoztatva, ha kell, feltehetjük, hogy . Hasonlítsuk össze ekkor -t az , ha , , szám -eshez tartozó Itt feltétel szerint mind a 3 tényező pozitív és pozitívak az kifejezésében szereplő további tényezők is, tehát Ha az számok nem mind egyenlők, az eljárást ismételhetjük, mert a szorzat közben mindig 1 marad. Legkésőbb lépés után minden 1 lesz. Mivel közben a fellépő értékek növekednek, azt kapjuk, hogy 3. feladat. Adott a síkon pont, és , amelyek közül semelyik három nincs egy egyenesen. Tudjuk, hogy bármelyik két különböző , ponthoz található olyan pont, hogy a háromszög belsejében van. Mutassuk meg, hogy páratlan szám. 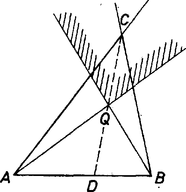 Valóban, ha a háromszög belsejében van, akkor az egyenesnek a -t nem tartalmazó partján van, a egyenesnek pedig az -t nem tartalmazó partján. Így a két félsík közös részében, tehát az állításban szereplő szögtartományban van. A konvex szögtartományról van szó, tehát arról, amelyik bármely két pontjával azok összekötő szakaszát is tartalmazza, miután a félsík konvex tartomány és konvex tartományok közös része is konvex. Fordítva, ha a mondott szögtartományban van, akkor a egyenes -n túli meghosszabbítása metszi az szakaszt egy belső pontjában. A szakasz az háromszögben van, tehát annak belső pontja a háromszög belső pontja. A feladatra térve a egyenes egyik, mondjuk jobb partján levő pontok számát (-et nem számítva) jelöljük -rel, a bal parton levőket -sel. A jelölést, ha kell, változtassuk meg úgy, hogy a jobb parton a pontok legyenek, mégpedig úgy, hogy A és félegyenes -n túli félegyenesei közti szögtartományok a bal parton vannak és a különböző -khez tartozóknak nincs közös pontjuk. Minden ilyen tartományban van legalább egy a bal parti pontok közül, mert a , -hez megfelelő pontoknak segédtételünk szerint itt kell lenniük. A szögtartományok száma , így Megjegyzések. 1. A versenyzők túlnyomó része a megoldásban szereplő lemmát sok más, általában nem ilyen ügyes módon használta fel. Sokan egy egyenest forgattak a pont körül és annak két félegyenesét pirosra, ill. zöldre festettnek gondolva megállapították, hogy forgatás közben felváltva egyszer a piros, legközelebb a zöld félegyenes halad át egy-egy ponton. -os elforgatás után ér vissza az egyenes először egy már érintett ponthoz, de ezen most az egyenes másik félegyenese halad át, mint a kiindulásnál, ezért ezzel a másodszor érintett ponttal együtt összesen páros számú ponton halad át az egyenes, másrészt -en, tehát páratlan. Mások azt vették észre, hogy a feladat feltételei nem változnak, ha a pontokat a -ból induló, rajtuk átmenő félegyenesen elmozdítjuk, hiszen ha és , és , és egy-egy -ból induló félegyenesen van, akkor az és háromszöget nézve, vagy mindkettő belsejében tartalmazza -t, vagy egyik sem (2. ábra). Ennek alapján egy középpontú körre helyezték át a pontokat. Ha a kör -vel átellenes pontját -vel jelöljük, akkor megállapították, hogy a kör mentén haladva felváltva következik egy és egy pont. A pontok száma helyett az átmérőket számolták össze egy félkörre eső végpontjaik szerint. Ha a ponttal kezdjük a megszámlálást, akkor egy ponttal is fejezzük be, mert az első pont, amit már nem számolunk. Ebből ismét következik páratlan volta. 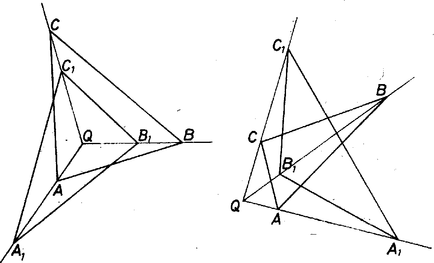 2. A versenyzők a segédtételt általában szemlélet alapján mondták ki. Ezt a bizottság nem tekintette hibának. 3. Többen megjegyezték, hogy a bizonyításban csak annyit használtunk ki, hogy egy , egy pont és nincs egy egyenesen, elég lett volna tehát ennyit feltételezni. Azt azonban már nem vették észre, hogy ezt meg nem kell külön feltenni, hiszen ha valamilyen -re és -re ez volna a helyzet, akkor semmilyen -ra nem tartalmazhatná a háromszög belsejében a -t, tehát nem teljesülhetne a feladat másik feltétele. 4. Sokan megjegyezték, hogy minden páratlan -re van a feltételeket kielégítő pontrendszer, pl. egy szabályos -szög csúcsait választjuk pontoknak és a középpontját -nak. Többen felvetették azt a kérdést, hogy ha megadunk tetszés szerint páratlan számú pontot a síkban, van-e hozzájuk olyan pont, amivel teljesülnek a feladat feltételei. A közölt megoldás felhasználásával megmutatjuk, hogy a kérdésre tagadó a válasz. A bizonyítás azt adta, hogy a egyenes egyik és másik partján ugyanannyi pontnak kell lennie. Itt helyett bármelyik pontot vehettük volna. Azt bizonyítottuk tehát, hogy ha a feladat feltételei teljesülnek, akkor mindegyik egyenes egyik és másik partján ugyanannyi pont van. Ha most 3 nem egy egyenesen levő pont van adva, akkor az általuk meghatározott háromszög minden belső pontja választható -nak. Nem nehéz belátni azt sem, hogy ha 5 pont van a síkban, azokhoz is található megfelelő pont. Ha azonban 7 pontot pl. a 3. ábrán látható módon adunk meg, akkor nem található hozzájuk megfelelő pont.  Valóban, a feladat feltételeinek fent megfogalmazott következménye szerint olyan kell hogy legyen, hogy pl. a egyenes mindkét partján 3‐3 pont legyen. Ez csak a szögtartomány belsejében levő pontokra teljesül. Hasonlóan benne kell lennie -nak a és a szögtartomány belsejében is. A 3 szögtartománynak azonban egyetlen közös pontja , és az is határpontja mindegyiknek, tehát nincs megfelelő pont. 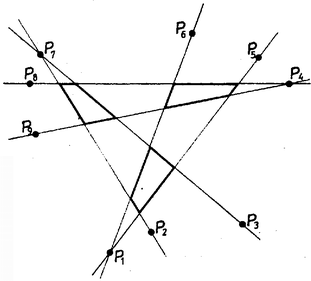 A 4. ábra 9 pontja közt 3 olyan szögtartományt jelöltünk meg, amelyeknek még közös határpontjuk sincs, viszont ha volna alkalmas pont, annak mindegyik belsejében kellene lennie. A következő megoldás a pontok megszámlálása helyett visszavezeti a problémát egy 2-vel kevesebb pontból álló rendszer esetére. II. megoldás. Megmutatjuk, hogy ha egy , pontrendszerre teljesülnek a feladat feltételei, akkor minden ponthoz található olyan pont, hogy az e két pont elhagyása után visszamaradó pontrendszerre is teljesülnek. Ebből már következik, hogy csak páratlan lehet, hiszen ha , pont közül pontpárok elhagyásával eljuthatunk páratlan számú pont esetén 3, páros számú esetén 2 pontból álló rendszerhez, amelyre szintén teljesülnek a feladat feltételei. De 2 pont, és esetén nem teljesülhetnek, hiszen egyáltalán nem választható hozzájuk egy harmadik pont, így semmilyen páros -re sem teljesülhetnek a feltételek. tehát csak páratlan lehet. Teljesüljenek a , pontokra a feladat feltételei. Kiválasztva tetszés szerint egy pontot, forgassuk a egyenest körül valamelyik irányban, míg egy újabb ponthoz nem ér. Nevezzük a pontokból és elhagyásával visszamaradó pontrendszert -nek. Mivel volt az első pont, amibe a forgatott egyenes elhagyása után beleütközött, a és egyenesek közti 4 szögtartomány közül egy csúcsszögeket alkotó párban nincs további pont. Az I. megoldásban bizonyított segédtétel szerint a , -hez megfelelő pontok a és szakaszok -n túli meghosszabbításai közti konvex szögtartomány belsejében vannak. Így ez és a szögtartomány tartalmazza -t. 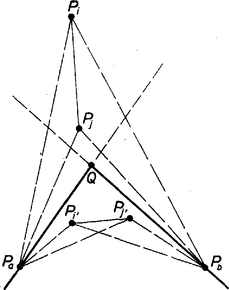 Legyen és -nek két pontja. Ha ugyanabban a szögtartományban vannak, akkor sem a , sem a háromszög nem tartalmazza -t (5. ábra), tehát a , -hez megfelelő pontok -hez tartoznak. Ha a szögtartományban van, a csúcsszög-tartományban, akkor feltehetjük, hogy a szakasz a félegyenest metszi egy pontban. Legyen olyan pont, amelyre tartalmazza -t (6. ábra). 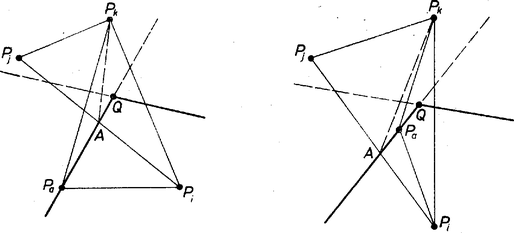 Mivel a -ból induló félegyenesen van, a háromszög is tartalmazza -t. Az utóbbi háromszög része a háromszögnek, így ez is tartalmazza -t, tehát a , pontpárhoz is megfelelő harmadik pont. a pontrendszer pontja, hiszen mint és -hoz megfelelő pont, az I. megoldás segédtétele szerint a szögtartomány csúcsszög‐tartományában van, és így a szögtartományon kívül; tehát különbözik -tól és -től. Ezzel beláttuk a megoldás elején megfogalmazott állítást és így a feladat állítását is. |