Cím: Hány nevezetes pontja van a háromszögnek?
Szerző(k):  Csirmaz László 
Füzet: 1984/december, 433 - 439. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltehetően mindenki egyetért azzal, hogy a súlypont, a magasságpont, a háromszög köré és a háromszögbe írt kör középpontja egyaránt nevezetes pontja a háromszögnek. Legutóbbi két számunkban Surányi László újabb nevezetes pontokkal ismertette meg olvasóinkat. * Felmerül a kérdés: tulajdonképpen hány nevezetes pontja is van egy háromszögnek ? Az alábbiakban egy paradox állítást bizonyítunk be, ami rámutat arra, hogy a ,,nevezetes'' és a ,,nem nevezetes'' pontok közti határvonalat mennyire nehéz meghúzni.

 

Nem lehet a háromszög összes belső pontja nevezetes, hiszen akkor a ,,nevezetes'' megkülönböztető jelző nem különböztetne meg egyetlen pontot sem a többitől. Az sem lehet, hogy csak egyetlen nemnevezetes pont legyen, hiszen ekkor ez a pont is nevezetes volna: nevezetesen arról, hogy ő az egyetlen nem nevezetes pont. Hasonlóan több, sőt nagyon sok nem nevezetes pontnak is kell lennie.
Másik oldalról az alábbi két, nevezetes pontokról szóló állítást feltehetően mindenki elfogadja:
 

(i) Egy háromszög csúcspontjai nevezetes pontok.
(ii) Ha az ABC háromszögben N1,N2 és N3 nevezetes pontok, akkor az N1N2N3 háromszög súlypontja is nevezetes.
 

Azt persze nem állítjuk, hogy csak ezek volnának a nevezetes pontok, de hogy ezek nevezetesek, az biztos.
(i) és (ii) meglehetősen egyszerűnek, sőt igaznak látszó feltételek. Az ártatlan külső alatt azonban ott lapul az alábbi meglepő következmény:
 

Tétel. Akárhogyan is veszünk fel az ABC háromszög belsejében egy kört, lesz a háromszögnek olyan nevezetes pontja, ami a kör belsejébe esik.
 

Más szavakkal: nincs egyetlen ,,tisztás'' sem a nevezetes pontok erdejében, a nevezetes pontok a háromszögben sűrűn helyezekednek el.
 

A bizonyítás egyszerűsítése érdekében bevezetünk egy új elnevezést. Egy P pontról azt mondjuk, hogy az mindegegy, * ha tetszőleges P középpontú körben található P-től különböző nevezetes pontja a háromszögnek. Könnyű belátni, hogy a bizonyítandó állítás ekvivalens a következővel:
 

(*) Az ABC háromszög minden belső és határpontja mindegegy.
 

A tétel bizonyítását egy önmagában is érdekes segédtétel, egy lemma * kimondásával és igazolásával kezdjük.
 

Lemma. Tegyük fel, hogy az ABC és az A'B'C' (esetleg elfajult) háromszögek olyanok, hogy az AA',BB', valamint CC' távolságok mindegyike kisebb ε-nál. Ekkor az ABC háromszög S súlypontjának és az A'B'C' háromszög S' súlypontjának a távolsága is kisebb ε-nál.
 

Bizonyítás. Mutassanak a közös kezdőpontból kiinduló a, b, c vektorok az ABC háromszög csúcsaiba, az a', b', c' vektorok pedig az A'B'C' csúcsaiba. Ekkor S-be az 13(a+b+c), S'-be pedig az 13(a'+b'+c') vektor mutat.
Az S és S' közötti távolság e két vektor különbségével, vagyis az
13(a+b+c)-13(a'+b'+c')=13[(a-a')+(b-b')+(c-c')],
vektor hosszával egyezik meg. Az a-a', b-b', valamint a c-c' vektor hossza az A és A', a B és B', illetve C és C' közti távolsággal egyenlő, tehát mindhárom vektor rövidebb ε-nál. Összegük, vagyis (a-a')+(b-b')+(c-c'), a háromszög-egyenlőtlenség miatt rövidebb 3ε-nál, tehát az összeg harmada, vagyis az S'-ből S-be mutató vektor hossza is rövidebb ε-nál. Ezt akartuk bizonyítani.
 

Most rátérünk a tétel, pontosabban a (*) alatti állítás bizonyítására.
 

1. Elsőként azt igazoljuk, hogy a háromszög oldalfelező pontjai ,,mindegegyek''. Legyen tehát F például az AB oldal felező pontja, és definiáljuk az S,S1,... pontokat a következőképpen. S az ABC háromszög súlypontja, S1 az ABS súlypontja, S2 az ABS1 súlypontja és így tovább (1. ábra).
 
 
1. ábra
 

Világos, hogy ezek mind nevezetes pontok, mind rajta vannak az ABC háromszög CF súlyvonalán, valamint hogy FS=FC/3,FS1=FS/3=FC/9, FS2=FS1/3=FC/27, és általában
FSn=FC3n+1.
Mivel n növekedtével 3n+1 minden határon túl nő, azért akárhogyan is veszünk fel egy F középpontú kört, abba az Sn pontok véges sok kivételével mind beleesnek. Így F valóban mindegegy.
 

2. Másodszorra azt mutatjuk meg, hogy a háromszög mindhárom csúcsa mindegegy. Ez nem következik abból, hogy a csúcsok nevezetes pontok, hiszen például egy A körüli tetszőleges körben A-tól különböző nevezetes pontot kell találnunk. Célunkat kerülővel érjük el: egy sor ,,segédpontról'' mutatjuk meg, hogy mindegegy, majd ebből következtetünk arra, hogy A is az.
Az előbb láttuk, hogy S,S1... mind nevezetes pontok. Az ASiSi+1 háromszögek Ti súlypontjai ugyancsak nevezetesek, és ezek mindannyian egy CF-fel párhuzamos egyenesen helyezkednek el. Messe ez az egyenes az AB szakaszt F1-ben, F1 az AF-nek F-hez közelebbi harmadolópontja lesz. Az ASS1 háromszög AT0 súlyvonala felezi az SS1 szakaszt, ezért F1T0<FS (egészen pontosan F1T0=49FS). Hasonlóan
F1Tn<FSn=FG3n+1.
A Tn pontok mind nevezetesek, és bármely F1 körüli körbe véges sok kivételével valamennyi beleesik, ezért F1 is mindegegy.
Következőként az ATiTi+1 háromszögek Ui súlypontjait vizsgáljuk. Ezek ugyancsak egy CF-fel párhuzamos egyenesen helyezkednek el, és ennek az AB-vel való F2 metszéspontjára
AF2=23AF1=(23)2AF.
Mivel F2Un<F1Tn<FSn, ezért az Un pontok egyre közelebb kerülnek F2-höz: F2 is mindegegy.
Hasonlóan F3 is mindegegy, ahol F3 az AF2 szakasz F2-höz közelebbi harmadolópontja, azaz
AF3=23AF2=(23)3AF.
Általában az AF szakasznak az az Fn pontja is mindegegy, amire
AFn=(23)nAF.

Innen már könnyen következik, hogy az ABC háromszög A csúcsa is mindegegy. Vegyünk fel A körül egy tetszőleges k kört. Állítjuk, hogy van k-ban A-tól különböző nevezetes pont. Tudjuk, hogy (2/3)n az n növekedtével tart a nullához, tehát az Fn pontok véges sok kivételével, mind k belsejébe esnek; legyen Fi ezek közül egy (2. ábra). Rajzoljunk Fi körül olyan k1 kört, ami teljes egészében k belsejében van, és nem tartalmazza A-t. Az Fi-ről tudjuk, hogy mindegegy, ezért van k1 belsejében (Fi-től különböző) nevezetes pont, legyen az egyik ilyen N. Az N különbözik A-tól és belső pontja k-nak: a keresett pontot megtaláltuk. Így A valóban mindegegy, ahogyan állítottuk.
 
 
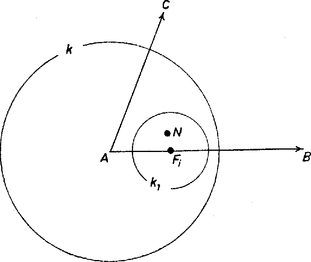2. ábra
 

 

3. A csúcsokról már tudjuk, hogy mindegegyek, most a háromszög kerületének összes pontjáról igazoljuk ugyanezt. Újfent kerülő útra kényszerülünk: első nekifutásra csak azt mutatjuk meg, hogy az AB szakasz pontjai közül ,,elég sok'' mindegegy.
Legyen tehát M1 és M2 az AB szakasz két olyan pontja, melyekről már tudjuk, hogy mindegegyek. (Például kezdetben legyen M1=A és M2=B.) Állítjuk, hogy az M1M2 szakasz mindkét harmadolópontja is mindegegy. Legyen H az M2-höz közelebbi harmadolópont (a másik eset hasonlóan kezelhető), és rajzoljunk H körül egy ε sugarú k kört (3. ábra).
 
 
3. ábra
 

Azt kell megmutatnunk, hogy k-ba esik nevezetes pont. Rajzoljunk M1 és M2 köré is egy-egy ε sugarú kört, az előbbi legyen k1, az utóbbi k2. Feltevésünk szerint M1 és M2 is mindegegy, ezért k1-nek és k2-nek is van nevezetes belső pontja: N1 illetve N2. Az M2 középpontú, M2N2 sugarú körben is van nevezetes pont, mondjuk N3. Az N1,N2,N3 három különböző nevezetes pont, tehát N súlypontjuk is nevezetes. Állítjuk, hogy N belső pontja a k körnek és így megtaláltuk, amit kerestünk.
Ez utóbbi állítás igazolására a lemmát használjuk az N1N2N3, valamint az M1M2M2 (elfajult) háromszögekre. Az N1,N2 és N3 pontok választása alapján az N1M1,N2M2 és N3M2 távolságok mindegyike kisebb ε-nál. Az N1N2N3 háromszög súlypontja N, az M1M2M2 ,,háromszögé'' pedig H. A lemma alapján tehát az NH távolság is kisebb ε-nál: N valóban belső pontja k-nak. (Az olvasóra hagyjuk annak belátását, hogy az N1,N2,N3 pontokat lehet választani úgy is, hogy valódi háromszöget alkossanak, vagyis N1,N2 és N3 ne essen egy egyenesre.)
Ennek alapján az AB szakasz mindkét harmadolópontja mindegegy, azután az így előálló három szakasz mindegyikének harmadolópontjai is mindegegy, az azokat harmadoló pontok is stb. (4. ábra). Vagyis ha valamilyen pozitív egész n-re az AB szakaszt 3n egyenlő részre osztjuk, az összes osztópont mindegegy lesz.
 
 
4. ábra
 

Most már bizonyítani tudjuk, hogy az AB szakasz összes pontja is mindegegy. A szakasz tetszőleges P pontja köré tetszőleges k kört rajzolva a kör belsejébe esik osztópont, ha n-et úgy választjuk, hogy 3n nagyobb legyen a kör átmérőjének reciprokánál. Erről az M osztópontról tudjuk, hogy mindegegy. Így M körül bármekkora k1 kört rajzolva találunk k1-ben nevezetes pontot. De k1-et tudjuk úgy választani, hogy teljes egészében k-ban legyen ‐ tehát k-ban is van (P-től különböző) nevezetes pont (5. ábra).
 
 
5. ábra
 

4. Az eddigiek alapján a háromszög kerületének minden pontja mindegegy. Az, hogy a háromszög minden belső- és határpontja is mindegegy ‐, vagyis a bizonyítandó (*) állítás ‐ innen az alábbiak alapján azonnal adódik:
 

1) Mindegegy pontokból álló háromszög súlypontja is mindegegy.
2) Ha P az ABC háromszög belső pontja, akkor találhatók a háromszög kerületén olyan (nem egy egyenesre eső) U,V,W pontok, hogy P súlypontja az UVW háromszögnek.
 

A cikk elején kimondott tétel bizonyítását (és ezzel magát a cikket is) befejeztük, mihelyst ezt a két állítást igazoltuk.
(1)-hez legyenek M1,M2 és M3 mindegegy pontok, M pedig az M1M2M3 háromszög súlypontja. Válasszunk egy pozitív ε számot, azt kell belátnunk, hogy van olyan nevezetes pont, melynek M-től mért távolsága kisebb ε-nál. Mivel M1,M2 és M3 mindegegy pontok, azért vannak olyan N1,N2 és N3 nevezetes pontok, melyekre az M1N1,M2N2 és M3N3 távolságok mindegyike kisebb ε-nál. Az N1N2N3 háromszög N súlypontja is nevezetes pont, távolsága M-től a lemma alapján kisebb ε-nál, amivel készen vagyunk.
 
 
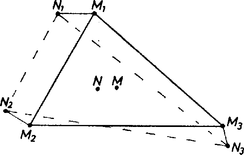6. ábra
 

Vagy mégsem ? Nem bizony ! Meg kell mutatnunk, hogy N1,N2 és N3 választható úgy, hogy valódi háromszöget alkossanak ‐ ez megtehető, ha M1M2M3 is valódi háromszög volt. Hogy hogyan, annak meggondolását az olvasóra bízzuk. Végül előfordulhat, hogy N és M egybeesik, noha nekünk M-től különböző nevezetes pontra van szükségünk. Ebben az esetben N1-et és N2-t megtartva, N3 helyett olyan N'3 nevezetes pontot válasszunk, mely M3-hoz N3-nál is közelebb van. Az N1N2N3 és az N1N2N'3 súlypontja nem esik egybe (a két súlypontot összekötő vektor éppen az N3N'3 vektor harmadrésze), így ez most már különbözik M-től. (1)-et valóban bizonyítottuk.
 
 
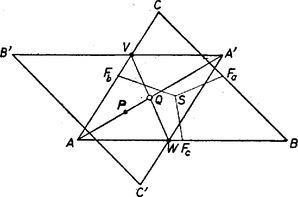7. ábra
 

(2) bizonyítására kössük össze az ABC háromszög S súlypontját az FA,FB, FC oldalfelező pontokkal. Ezzel a háromszög belsejét három négyszögre osztottuk fel, ezek egyikébe (vagy annak határára) esik a P pont, mondjuk abba, amelyiknek az A is csúcsa (7. ábra). A keresett UVW háromszög U csúcsa legyen A, súlypontja pedig P. Így a másik két, V és W csúcsokat összekötő szakasz Q felezőpontját megkaphatjuk úgy, hogy az AP félegyenesre felmérjük az AQ=32AP távolságot. Ez a Q pont továbbra is belső pontja az ABC háromszögnek ‐ kivéve ha P éppen egybeesik S-sel, de akkor Q a kerületre esik és a (2) állítás automatikusan teljesül. Így feltehetjük, hogy Q belső pont. A V és W pontokat úgy kaphatjuk, hogy az ABC háromszöget tükrözzük Q-ra. Az így adódó A'B'C' háromszög kerületének, valamint az ABC háromszög kerületének közös pontjai közül bármelyik A-tól és A'-től különböző jó V-nek, annak Q-ra való tükörképe pedig W-nek.
Valóban, ekkor A,V és W az ABC háromszög kerületének pontjai; súlypontjuk pedig P. Végül A,V és W nem eshetnek egy egyenesbe, hiszen akkor P-nek is ugyanerre az egyenesre kellene esnie, és így nem lehetne az AFCSFB négyszög pontja.
Azt kell még meggondolnunk, hogy az ABC és A'B'C' háromszögeknek van a csúcsoktól különböző közös kerületi pontjuk. Ez pedig azért van így, mert Q belső pontja mindkét háromszögnek. Egy háromszöget és 180∘-os elforgatottját pedig nem lehet úgy elhelyezni a síkon, hogy közös belső pontjuk ugyan legyen, de csúcstól különböző közös határpontjuk ne.
Ezzel igazoltuk a cikk elején kimondott tételt: egy háromszög nevezetes pontjai a háromszög belsejét sűrűn töltik ki. No persze ezek mindegyike nem annyira nevezetes, mint mondjuk a magasságpont vagy a beírt kör középpontja, de nevezetes annak értelmében, amit a ,,nevezetességről'' állítottunk.
Ez a paradox ‐ első pillanatban hihetetlen, ám mégis igaz ‐ tétel, ha kicsit mesterkélten is, de rámutat a matematika alkalmazásakor lépten-nyomon előforduló jelenségre. Vizsgálunk valamit ‐ jelen esetben a háromszög nevezetes pontjait. Megfogalmazzuk a matematikai modellt ‐ most a nevezetes pontokról szóló (i) és (ii) feltételt ‐, majd magáról a modellről (és nem a vizsgált jelenségről !) állításokat bizonyítunk. Ezek ellentmondhatnak annak, amit józan ésszel elvárunk ‐ túl sok nevezetes pont lett. Mi a teendő ? Vagy a matematikai modell volt hibásan felállítva (tehát a nevezetes pontok a rájuk szabott két feltétel közül valamelyiket mégsem elégítik ki), vagy pedig szemléletünk adott hibás képet a jelenségről: a nevezetes pontok várakozásunkkal ellentétben tényleg sokan vannak.
A dilemmának nincs megoldása: az olvasónak magának kell döntenie, melyik változatot fogadja el. S bár itt választásának lényegében nincs tétje, hasonló, de már vérre menő dilemma merül fel a modern fizika matematikai modelljeinél: vajon a (mikro-) fizikai valóságot modelleztük hibásan, vagy az a fizikai világ más-e egészen, mint amit megszoktunk ?
*Surányi László: A háromszög kevésbé ismert nevezetes pontjairól (KÖMAL 34. évfolyam 7-8-9. szám).

*A ,,mindegegy'' jelző Karinthy Frigyes egyik halandzsaverséből való. A szonett ‐ sajnos csak töredékes formában ‐ Karinthy Mint vélgaban című glosszájában olvasható (a glossza pedig A Tükör és a maszk antológiában):

 

Fájdala
 
A pő, ha engemély kimár ‐
De mindegegy ha vildagár...
      ... Mert engemély minder bagul,
Mint vélgaban a bégahúr !   

*A Természettudományi Lexikon szerint ,, lemma görögül 'feltevés' segédtétel. A régebbi dialektikában (különösen Arisztotelésznél) bármilyen kevésbé fontos bizonyított vagy akár bizonyítás nélkül elfogadott tétel, amelyből valamely nála fontosabb állítást levezetünk. Archimedesznél hol feltevés, hol meg segédtétel jelentésű. Később a szó utóbbi jelentése vált általánossá.'' A Matematikai Kislexikon pedig a következőket írja: ,,valamely tétel bizonyítása során gyakran célszerű bizonyos olyan részállításokat megfogalmazni, melyek önmagukban is érdekesek, vagy pedig a bizonyítás során többször felhasználásra kerülnek. Ezeket az ún. segédtételeket lemmának is szokták nevezni.''