Cím: A háromszög kevésbé ismert nevezetes pontjairól II. rész
Szerző(k):  Surányi László 
Füzet: 1984/november, 337 - 351. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy téglalapot az ABC háromszög AB oldala fölé írt téglalapnak nevezünk, ha két csúcsa az AB oldalegyenesen, másik két csúcsa pedig a BC, illetve CA oldalegyenesen van. Hasonlóan definiáljuk az AC, valamint BC oldalak fölé írt téglalapokat is.
Nevezetes probléma a következő: adott háromszöghöz található-e mindig három olyan téglalap, amelyeknek középpontja közös, és a háromszög egy-egy oldala fölé vannak írva? A kérdés megválaszolásának egy lehetséges módja, hogy megkeressük az egyik oldal fölé írt téglalapok középpontjainak mértani helyét*.

 

11. tétel. A háromszög egyik oldala fölé írt téglalapok középpontjainak mértani helye az oldal felezőpontját a hozzá tartozó magasságszakasz felezőpontjával összekötő egyenes. (Az egyenesnek az oldallal és a magassággal való metszéspontjaihoz elfajuló téglalapok tartoznak.)
 
 
1. ábra
 

A tételt az AB oldalra igazoljuk. Legyen PQRS az AB fölé írt téglalap (1. ábra). A QR szakasz felezőpontja rajta van a CFab súlyvonal egyenesén. Vetítsük merőlegesen C-t és a QR szakasz Fqr felezőpontját az AB oldalra. A kapott T és U pontokra CT párhuzamos FqrU-val. A PQRS téglalap K középpontja ez utóbbi szakasz felezőpontja. Mivel Fqr rajta van a CFab egyenesen, K rajta van a CFabT háromszög Fab csúcsból induló súlyvonalegyenesén. Ez az egyenes az Fab oldalfelezőpontot a CT magasságszakasz Fcf felezőpontjával köti össze. A gondolatmenet megfordítható, segítségével az egyenes minden K pontjához szerkeszthető AB fölé írt, K középpontú téglalap, kivéve ha K az AB vagy a CT egyenesre esik. Ha AC=CB, a mértani hely a C-ből induló magasság (az Fab és Fct pontok kivételével).
Ahhoz tehát, hogy létezzenek az oldalak fölé írt, közös középpontú téglalapok, pontosan arra van szükség, hogy a 11. tételben definiált három egyenes egy ponton menjen keresztül. De vajon igaz-e ez? Belátjuk, hogy a válasz igenlő:
 

12. tétel. A magasságszakasz felezőpontját a szemközti oldal felezőpontjával összekötő három egyenes egy ponton megy keresztül. Ez a pont a háromszög Lemoine‐Grebe-féle pontja, és L-lel fogjuk jelölni.
 
 
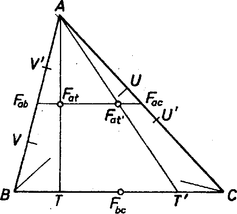2. ábra
 

Legyen az A-ból, B-ből és C-ből induló magasság talppontja rendre T, U, V, a talppontok tükörképe a megfelelő oldal felezőpontjára T', U', V' (2. ábra). A 4. tétel szerint az AT', BU', CV' Ceva-szakaszok egy pontban találkoznak. Másrészt pl. BT=CT',ígyFabFat=Fat'Fac=12T'C. Ha S-ből -1/2 arányú kicsinyítést hajtunk végre, A képe Fbc , C képe Fab és T' képe Fat lesz, tehát AT' képe FbcFat. Ugyanígy BU' és CV' képe FacFbu, ill. FabFcv. Egy ponton átmenő egyenesek tükörképei is egy pontban találkoznak, tehát így az oldalfelezőpontokat a megfelelő magasság felezőpontjával összekötő szakaszok valóban egy pontban találkoznak.
A bizonyítás során az AT, BU, CV Ceva-szakaszokról annyit használtunk ki, hogy egy pontban találkoznak. Beláttuk tehát a következő tételt:
 

13. tétel. Ha az AT, BU, CV Ceva-szakaszok egy pontban találkoznak, akkor (és csak akkor) e Ceva-szakaszok felezőpontját a szemközti oldal felezőpontjával összekötő három egyenes, FabFcv,FacFbuésFbcFat is egy ponton megy keresztül.
 

A 11. és 12. tétel alapján a fejezet elején felvetett kérdésre tehát igenlő választ adhatunk. Pontosan egy olyan L pont van, amely egyszerre középpontja a három oldal fölé írt egy-egy téglalapnak: Sőt: L-en kívül nincs olyan pont, amely akár két oldal fölé írt téglalapnak közepe lenne.
A felvetett kérdést látszólag teljesen elintéztük. Valójában a három oldal fölé írt, L közepű téglalapoknak sok érdekes tulajdonsága van, s ez az L pont számos tulajdonságára is fényt vet.
 
 
3. ábra
 

Tükrözzük L-re a BC oldalt, messe a tükörkép az AB egyenest Q-ban, AC-t R-ben. Legyen Q és R merőleges vetülete a BC oldalon P és S (3. ábra), PQRS téglalap lesz. Ha L középpontja  egy BC fölé írt téglalapnak, ez a téglalap középpontosan szimmetrikus L-re, tehát csakis ez a PQRS téglalap lehet. De ekkor R és Q tükörképe éppen P és S. Tükrözzük most L-re az AC egyenest. AC-n rajta van R, ezért P rajta van a tükörképén, vagyis a tükörkép-egyenes a BC oldalt P-ben metszi, messe az AB oldalt U-ban. Tudjuk, hogy van AC fölé írt, L középpontú téglalap. Ez a téglalap tükrös L-re, tehát három csúcsa csakis P, U, R lehet. Negyedik csúcsa pedig U-nak L-re vonatkozó tükörképe, V. Vegyük észre, hogy ekkor QVSU szintén téglalap, hiszen tükrös L-re, átlói metszéspontjára, továbbá QS=RP=UV, tehát átlói egyenlőek. Vagyis QVSU az AB fölé írt téglalap! Ismét beláttuk tehát, hogy ha van L középpontú BC és AC fölé írt téglalap, akkor van L középpontú AB fölé írt téglalap is.
 

14. tétel. Egyetlen olyan pont van a síkon, amely egyszerre középpontja egy-egy BC és AC fölé írt téglalapnak, ez a pont a háromszög Lemoine‐Grebe-féle pontja. A két téglalapnak egy szemben fekvő csúcspára közös. A másik két csúcspár az AB fölé írt, L közepű téglalapot határozza meg. A három téglalap hat csúcsa egy L közepű körön van.
 

Az URS∢ és ACB∢ merőleges szárú szögek, tehát URS∢=γ. Ugyanígy RUS∢=α és USR∢=β, ezért az USR és ABC hasonló háromszögek:
SR:RU:US=BC:CA:AB.
Másrészt L távolsága a BC, CA, AB oldalaktól rendre 12SR, 12RU és 12US, amiből az alábbi tételt kaptuk:
 

15. tétel. Az L pontnak az AB, BC, CA oldalaktól mért távolságai úgy aránylanak egymáshoz, mint e három oldal hossza.
 

Látni fogjuk, hogy ez a tulajdonság egyértelműen jellemzi a Lemoine‐Grebe-pontot. Tekintsük az UQRS húrnégyszöget! Láttuk, hogy URS∢=ACB∢. Másrészt a kerületi szögek tétele szerint URS∢=UQS∢, tehát BQS∢=γ, hasonlóan BSQ∢=α. Ha egy QS szakasz végpontjai AB-n, ill. BC-n vannak, továbbá AB-vel γ, BC-vel α szöget zár be, akkor a QS-t AC-vel antiparalelnek nevezzük. A háromszög oldalaival antiparalel például a magasságpont talpponti háromszögének oldalai. Láttuk, hogy QS antiparalel AC-vel. Természetesen PR antiparalel AB-vel és UVBC-vel. Valamely oldallal antiparalel szakaszok párhuzamosak egymással, tehát L-en keresztül minden oldallal csak egy antiparalel húzható. A következő tételhez jutunk:
 

16. tétel. Ha L-en keresztül a három oldallal antiparalel szakaszokat fektetünk, a szakaszok egyenlő hosszúak és L felezi őket (tehát végpontjaik egy L közepű körön vannak). Bármely két szakasz végpontjai ‐ valamelyik oldal fölé írt ‐ L közepű téglalapot alkotnak.
 

*

 

5. feladat. Igazoljuk, hogy L távolsága az ABC háromszög oldalaitól rendre
2ta2+b2+c2⋅a,2ta2+b2+c2⋅bés2ta2+b2+c2⋅c,
ahol t az ABC háromszög területét jelöli.
 

*

 
 
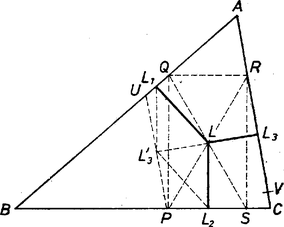4. ábra
 

Jelöljük L vetületét az UQ, PS és UP szakaszon rendre L1,L2,L'3-mal (4. ábra). L1 felezi az UQ szakaszt, L2 a PS szakaszt és L'3 az UP szakaszt. Tehát LL1L'3L2 négyszög paralelogramma, hiszen az SQUP négyszög oldalainak felezőpontjaiból alkotott négyszög, és bármely négyszög felezőpontjaiból alkotott négyszög paralelogramma (1. pl. Geometriai feladatok gyűjteménye I. 558. feladat). Tehát LL'3 és L1L2 felezi egymást. Legyen L vetülete az RV szakaszon L3. RV||UP, ezért L3,L,L'3 egy egyenesen van. Ezért az LL3 egyenes felezi az L1L2 szakaszt, vagyis LL3 egyenes az L1L2L3 háromszög L1L2 oldalához tartozó súlyvonal. Az okoskodás az L1L2L3 háromszög másik két oldalára is elmondható, tehát L az L1L2L3 háromszög súlyvonalainak metszéspontja, vagyis az L1L2L3 háromszög súlypontja.
Az X pont talpponti háromszögének nevezzük ‐ egy adott háromszögre vonatkozóan ‐ azt az X1X2X3 háromszöget, amelynek három csúcsa X merőleges vetülete a három oldalon. (A szokásos értelemben vett talpponti háromszög tehát a magasságpont talpponti háromszöge.) Ezzel az elnevezéssel eredményünk következőképp fogalmazható:
 

17. tétel. A Lemoine‐Grebe-pont súlypontja a saját talpponti háromszögének.
Igaz ennek megfordítása is:
 

17'. tétel. A Lemoine‐Grebe-pont az egyetlen olyan pont, amely súlypontja saját talpponti háromszögének.
 

Ennek bizonyításához szükségünk lesz a következő, önmagában is szép tételre, amely bizonyos értelemben a 14. és 16. tételek "megfordítása''.
 

18. tétel. Tükrözzük az XYZ háromszöget S súlypontjára, jelöljük a tükörképet X'Y'Z'-vel. X-ben, X'-ben XX'-re; Y-ban, Y'-ben YY'-re; Z-ben, Z'-ben ZZ'-re merőlegest állítva egy hatszöget kapunk. E köré kör írható, melynek középpontja S, továbbá a hatszög szemközti oldalai téglalapokat alkotnak.
 
 
5. ábra
 

Legyen a kapott hatszög hat csúcsa az 5. ábra szerinti sorrendben P1P2P3P4P5P6 (ez hurkolt hatszög is lehet). A hatszög tükrös S-re, tehát két-két szemben fekvő csúcspár paralelogrammát alkot. Ha belátjuk, hogy XX', YY', ZZ' e paralelogrammák középvonala, akkor pl. P1P3 párhuzamos XX'-vel, következésképp P1P3 merőleges P3P4-re és P6P1-re, tehát P1P3P4P6 valóban téglalap. Hasonlóan P1P2P4P5 és P2P3P5P6 is téglalap, tehát a hatszög köré írható kör, és annak középpontja S.
Elég tehát belátni, hogy pl. a P1P6P4P3 paralelogrammának XX' középvonala, és ehhez elég annyit belátni, hogy X felezi a P1P6 szakaszt. Tükrözzük P1-et XZ' felezőpontjára, legyen a tükörkép Q. XQ→=P1Z'→ és P1Z'→ merőleges az SZ' egyenesre, tehát XQ is merőleges SZ'-re. Ugyanígy QZ'→=XP1→ és XP1→ merőleges az SX egyenesre. XQ és Z'Q tehát az SXZ' háromszög magasságai, Q pedig e háromszög magasságpontja. Az okoskodás megismétlésével azt kapjuk, hogy ha P6-ot az XY' felezőpontjára tükrözzük, a kapott R tükörkép az SXY' háromszög magasságpontja. S súlypontja az XYZ és X'Y'Z' háromszögeknek, ezért S-et az Y'Z' szakasz U felezőpontjára tükrözve X-et kapjuk (ugyanis 2SU=SX'=SX). Következésképp az SXZ' háromszöget U-ra tükrözve az XSY' háromszög adódik, a Q magasságpont tükörképe pedig R. Ebből Y'R→=QZ'→. De Y'R→=P6X→ és QZ'→=XP1→, tehát P6X→=XP1→, X valóban felezi a P6P1 szakaszt. Ezzel a 18. tételt bebizonyítottuk.
 
 
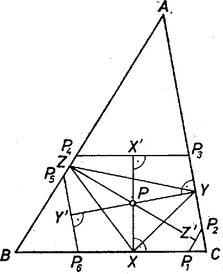6. ábra
 

Most rátérünk a 17'. tétel bizonyítására. Legyen P olyan pont, amely súlypontja saját talpponti háromszögének. Belátjuk, hogy, mindhárom oldal fölé írható egy-egy P közepű téglalap. Legyen P merőleges vetülete a BC,CA,AB oldalakon rendre X, Y, Z (6. ábra). Feltevésünk szerint P súlypontja az XYZ háromszögnek. Tükrözzük X,Y,Z-t P-re, a tükörképek legyenek X', Y', Z'. Állítsunk merőlegest X-ben és X'-ben XX'-re, Y-ban és Y'-ben YY'-re és Z-ben, Z'-ben ZZ'-re, az X, Y, Z-ben állított merőlegesek éppen a háromszög oldalai lesznek. A hat merőleges által alkotott hatszög hat csúcsa tehát a háromszög oldalain van. Legyen a hat csúcs a 6. ábra szerint P1P2P3P4P5P6. A 18. tétel alapján P1P3P4P6,P1P2P4P5 és P2P3P5P6 téglalap, és mindháromnak P a középpontja. E három téglalap rendre a BC, AB, CA oldal fölé írt P közepű téglalap. P tehát a 14. tétel pontjának tulajdonságaival rendelkezik, így köteles a háromszög Lemoine‐Grebe-pontja lenni. Ezzel a bizonyítást befejeztük.
A 17'. tétel segítségével egy szélsőérték problémát is megoldhatunk. Nevezzük a PQR háromszöget az ABC háromszög beírt háromszögének, ha három csúcsa az ABC háromszög három oldalának egy-egy pontja. Ismeretes, hogy a beírt háromszögek közül a magasságpont talpponti háromszögének legkisebb a kerülete. Most belátjuk, hogy egy beírt háromszög oldalainak négyzetösszege akkor minimális, ha az a Lemoine‐Grebe-pont talpponti háromszöge. Legyen ugyanis PQR olyan beírt háromszög, amire ez a négyzetösszeg minimális, és legyen a P, R pontok vetülete az AC oldalon P', R' (7. ábra). Jelölje F a P'R' szakasz felezőpontját. Legyen az AC szakasz egy tetszőleges pontja X, és x az XF szakasz előjeles hossza.
 
 
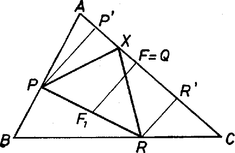7. ábra
 

A PP'X és RR'X derékszögű háromszögekre felírjuk a Pitagorasz-tételt, és felhasználjuk, hogy P'F=FR'.
PX2+XR2=PP'2+(P'F-x)2+RR'2++(x+FR')2=PP'2+RR'2+2P'F2+2x2.




Ez pedig akkor minimális, ha x=0 azaz X=F. Következésképp ha PQR háromszög oldalainak négyzetösszege minimális, akkor Q=F. Állítsunk F-ben merőlegest AC-re, s messe ez PR-t F1-ben. FF1, vagy ami ugyanaz, QF1 középvonala a PP'R'R derékszögű trapéznak, tehát F1 felezi PR-t, QF1 súlyvonala a PQR háromszögnek. Ezért PQR súlypontjának AC-re eső talppontja éppen Q. Hasonló igaz a PésR pontokra is, tehát az alábbi tételt kaptuk:
 

19. tétel. Ha a beírt PQR háromszög oldalainak négyzetösszege minimális, akkor a PQR háromszög saját súlypontjának talpponti háromszöge.
 

Összehasonlításul érdemes megjegyezni, hogy a háromszög magasságai szögfelezők a magasságpont talpponti háromszögében. Következésképp az ABC háromszögbe írt minimális kerületű háromszög saját beírt köre közepének talpponti háromszöge (l. pl. Coxeter‐Greitzer: Az újra felfedezett geometria, 37. oldal).
Végül a 19. és 18. tételből következik a
 

20. tétel. Ha a PQR beírt háromszög oldalainak négyzetösszege minimális, akkor a PQR háromszög a Lemoine‐Grebe-féle pont talpponti háromszöge.
 

*

 

6. feladat. Az eddig elmondottakból még nem következik, hogy a Lemoine‐Grebe pont talpponti háromszöge az a beírt háromszög, amelyben minimális az oldalak négyzetösszege. Miért nem?
 

7. feladat. Bizonyítsuk be, hogy ha a PQR beírt háromszögben az oldalak negyedik (általában 2k-adik pozitív egész) hatványának összege minimális, akkor PQR az L pont talpponti háromszöge.
Érdekes volna tudni, hogy akármilyen l természetes számra igaz-e, hogy ha a PQR beírt háromszögben az oldalak l-edik hatványának összege minimális, akkor a PQR háromszög valamely pont talpponti háromszöge. l=1-re ez igaz és páros l-re a 7. feladat szerint szintén igaz.
 

*

 

Most visszatérünk a 16. tételhez, s annak segítségével az L Lemoine‐Grebe-pont újabb tulajdonságait igazoljuk. Nyilvánvaló, hogy egy oldallal antiparalel szakaszok mind párhuzamosak, így e szakaszok felezőpontjai egy egyenest alkotnak, amely átmegy az oldallal szemközti csúcson, de maga a csúcs nem tartozik a mértani helyhez. Az is nyilvánvaló, hogy ha egy antiparalel szakaszt tükrözünk a szemközti csúcs belső szögfelezőjére, a tükörkép az oldallal párhuzamos szakasz, aminek végpontjai a szemközti csúcsból induló két oldalon vannak. Az ilyen szakaszok felezőpontjainak mértani helye a súlyvonal. A következő tételhez jutottunk:
 

21. tétel. Az AB oldallal antiparalel szakaszok felezőpontjainak mértani helye egy C-n átmenő egyenes, melynek a C-ből induló belső szögfelezőre való tükörképe a súlyvonal. Ezt az egyenest a C-ből induló szimmediánnak nevezik, tc-vel fogjuk jelölni.
 

A szimmediánok a háromszög kevéssé ismert, de fontos transzverzálisai. Látni fogjuk, hogy tulajdonságai szervesen illeszkednek a háromszög nevezetes pontjai és szakaszai közé (vö. a 20. tétel után mondottakkal).
 

*

 

8. feladat. Legyen az ABC háromszög A-ból és B-ből induló magasságainak talppontja T és U. Igazoljuk, hogy a tc szimmedián felezi az UT szakaszt.
 

*

A 16. tétel szerint az L pont felezi a rajta átmenő, a háromszög oldalaival antiparalel szakaszokat. Ekkor a 21. tétel szerint L rajta van mindhárom csúcsból induló szimmediánon. Igaz tehát az alábbi tétel:
 

22. tétel. A háromszög három szimmediánja egy pontban találkozik, a háromszög Lemoine‐Grebe-féle pontjában.
 

Az L pont következő tulajdonságának igazolásához egy egyszerű definícióra és egy segédtételre van szükségünk. Az ABC háromszög síkjában levő P pontnak egy oldaltól vett előjeles távolsága pozitív, ha P az oldalegyenesnek arra az oldalára esik, ahol a háromszög szemközti csúcsa van. Ha P a másik félsíkba esik, a távolság negatív, magán a oldalegyenesen persze 0.
 

Segédtétel. Azoknak a pontoknak a mértani helye, amelyek távolsága a BC és CA oldalegyenestől adott x:y arányú, egy, a C csúcson átmenő egyenes. Ha ezt az egyenest a C csúcsból induló belső szögfelezőre tükrözzük, akkor az új egyenes pontjainak távolsága a BC és CA oldalaktól y:x=1x:1y arányú. (Feltesszük, hogy xy≠0, egyébként x, y tetszőleges.)
A segédtétel első fele közismert. Második fele következik abból, hogy ha a C-ből induló szögfelelzőre tükrözünk, BC és CA helyet cserél.
 

*

 

9. feladat. Hogyan módosul a segédtétel állítása, ha a C-ből induló külső szögfelezőre tükrözünk?
 

*

 
 
8. ábra
 

Legyen az AB oldal Fab felezőpontjának távolsága BC-től p, CA-tól q (8. ábra). A CBFab és a CAFab háromszögek BFab és AFab oldala, valamint az ezekhez tartozó (közös) mc magasság egyenlő, tehát a háromszögek területe egyenlő. Következésképp CB⋅p=AC⋅q, tehát pq=ACCB. Fab rajta van a C-ből induló súlyvonalon, így a segédtételt felhasználva a következő tételhez jutunk:
 

23. tétel. A C-ből induló súlyvonal azoknak a pontoknak a mértani helye, amelyek távolsága a BC, CA oldaltól CA:CB arányú. A C-ből induló szimmedián azoknak a pontoknak a mértani helye, amelyek távolsága a BC, CA oldaltól CB:CA arányú.
 

A szimmediánnak most bizonyított tulajdonsága módot ad annak igazolására, hogy a 15. tétel állítása az ABC háromszög belső pontjai közül csakis a Lemoine‐Grebe pontra áll. Az ABC háromszög belső pontjának a három oldaltól vett távolsága nyilván pozitív. Ha a BC és CA oldaltól vett távolságok aránya BC:CA, akkor a fenti tétel szerint a pont rajta van a C-ből induló szimmediánon. Hasonlóan ha a BC, CA, AB oldalaktól vett távolságok (ilyen sorrendben) BC:CA:AB arányúak, akkor a pontnak mindhárom szimmediánon rajta kell lennie. Következésképp csak egy ilyen pont van, s ez a Lemoine‐Grebe pont. Beláttuk az alábbi tételt:
 

24. tétel. Egyetlen olyan pont van a háromszög belsejében, amelynek a BC, CA és AB oldalaktól vett távolsága (ilyen sorrendben) BC:CA:AB arányú. Ez a pont a háromszög Lemoine‐Grebe-pontja.
 

Az imént bizonyított tétellel kapcsolatban két dolgot érdemes megjegyezni. Egyrészt új bizonyítást kaptunk a 22. tételre, amely egyszerűbb is, mert nem használja az antiparalel szakaszok tulajdonságait, bár nem mutat rá közvetlenül a Lemoine‐Grebe-pont többi tulajdonságának és a szimmediánok kapcsolatára. A 27. tételben még egyszer igazoljuk, hogy a szimmediánok egy pontban találkoznak, ez az L pont újabb tulajdonságára fog fényt vetni.
Másrészt a most bizonyított tétel egy lényegesen általánosabb tétel bizonyítását is adja.
 

24'. tétel. Ha x, y, z pozitív számok, akkor a háromszög síkjában egyetlen olyan X(x:y:z) pont van, amelynek a BC, CA, AB oldalaktól vett távolsága (ilyen sorrendben) x:y:z arányú. Ez a pont találkozási pontja azoknak az e, f, g egyeneseknek, ahol e azoknak a pontoknak a mértani helye, amelyeknek az AB és AC oldaltól mért távolsága z:y arányú, s hasonlóan definiáljuk f-et és g-t.
Ha e-t az A-ból, f-et a B-ből, g-t a C-ből induló belső szögfelezőre tükrözzük, a tükörképek ismét egy ponton mennek át, az X'(1x:1y:1z) ponton, aminek távolsága a BC,CA,AB oldaltól (ilyen sorrendben) 1x:1y:1z arányú.
 

A bizonyításhoz elég a következőket meggondolni. A 23. tétel előtti segédtétel szerint az e, f, g mértani helyek valóban egyenesek. Ha x, y és z pozitív, e három egyenes áthalad a háromszög belsején és egy-egy csúcsán. Következésképp az e, f, g egyenesek páronként metszik egymást a háromszög belsejében. Bármely kettő metszéspontján át kell haladnia a harmadiknak, hiszen pl. e és f metszéspontjának a CA és AB oldalaktól vett távolsága (y:z):(x:z)=y:x arányú. A három egyenes közös pontjának az oldalaktól vett távolsága x:y:z arányú. Más ilyen pont nincs, hiszen az ilyen pontnak az e, f, g egyenesek mindegyikén rajta kell lennie.
A tétel második része következik abból, hogy az említett segédtétel szerint e-t a belső szögfelezőre tükrözve olyan e' egyenest kapunk, amely pontjainak távolsága az AB, AC oldaltól 1x:1y arányú. Hasonló állítás igaz az f' és g' egyenesekre is, e', f' és g' tehát éppen az X'(1x:1y:1z) pontban találkozik.
Marad a kérdés, hogy hogyan módosul a 24'. tétel, ha x, y, z-ről nem kötjük ki, hogy pozitívak, hanem csak annyit, hogy egyikük sem nulla. Az e, f, g mértani helyek ekkor is egyenesek, s ha közülük kettő metszi egymást, metszéspontjukon a harmadik is átmegy. Általában tehát e, f, g vagy egy pontban találkozik, vagy páronként párhuzamosak. Utóbbi esetben célszerű felvenni egy "végtelen távoli pontot'', ahol e, f, g és a velük párhuzamos egyenesek "metszik egymást'', és ezt a "pontot'' X(x:y:z)-vel jelölni. Ha ezekkel a "végtelen távoli pontokkal'' bővítjük a síkot (minden irányhoz egy-egy ilyen pont tartozik), akkor a 24'. tétel minden megszorítás nélkül érvényben marad. A tétel második részét azonban érdemes külön is megfogalmazni:
 

Következmény. Ha e, f, g az ABC háromszög három, egy ponton átmenő transzverzálisa, s mindegyiket tükrözzük a vele egy csúcsból induló belső szögfelezőre, akkor a kapott három tükörkép is vagy egy ponton megy át, vagy párhuzamosak.
 

Ha például e, f, g a három súlyvonal, ezek az S(ma:mb:mc) pontban találkoznak. Tükörképeik éppen a szimmediánok, metszéspontjuk az
L(1ma:1mb:1mc)=L(a:b:c) Lemoine‐Grebe-pont. Ha e, f, g a három magasság, ezek az M pontban találkoznak. A magasság tükörképe a megfelelő szögfelezőre a csúcsot a körülírt kör K közepével összekötő egyenes.
 
 
9. ábra
 

(A bizonyítás leolvasható a 9. ábráról: KFab merőleges AB-re, tehát párhuzamos a CV magassággal. KFab a körülírt kört az AB ív F felezőpontjában metszi, FC tehát a C-nél levő szög belső szögfelezője. De a párhuzamosság miatt VCF∢=CFK∢, másrészt CFK háromszög egyenlő szárú, tehát CFK∢=FCK∢. Ebből azt kapjuk, hogy a CF szögfelező valóban felezi a VCK szöget: a CV magasságegyenes tükörképe a CF belső szögfelezőre valóban a CK egyenes.) K távolsága a BC, CA, AB oldaltól rendre rcosα, rcosβ, rcosγ, ahol r a körülírt kör sugara. Tehát K(cosα:cosβ:cosγ) a körülírt kör középpontja. A 24'. tétel szerint tehát a magasságpont M(cosβcosγ:cosγcosα:cosαcosβ).
 

*

 

10. feladat. Bizonyítsuk be közvetlenül a magasságpontról szóló fenti állítást! Igazoljuk, hogy az M magasságpont távolsága a BC oldaltól 2rcosβcosγ.
 

11. feladat. Igazoljuk, hogy a Feuerbach-kör középpontjának távolsága a három oldaltól úgy aránylik egymáshoz, mint cos(β-γ), cos(α-γ), cos(β-α). Adjunk a szögek segítségével szükséges és elégséges feltételt arra, hogy a Feuerbach-kör közepe valamelyik oldal egyenesére essen!
 

12. feladat. Hogyan módosul a 24'. tétel állítása, ha pl. e-t (g-t és f-t) a háromszög megfelelő külső szögfelezőjére tükrözzük?
 

13. feladat. Jelölje kab azt a kört, amely keresztül megy az A,B pontokon, s amelynek a CA oldalegyenes érintője, kba pedig azt a kört, amely keresztülmegy az A, B pontokon és a CB egyenes az érintője. Hasonlóan definiáljuk a kac, kca, kbc, kcb köröket. Igazoljuk, hogy kab, kbc, kca körök egy X ponton mennek keresztül, kba, kcb, kac körök pedig egy X' ponton. (X és X' a háromszög ún. Brocard-pontjai.) Igazoljuk, hogy AX-nek az A-ból induló, BX-nek a B-ből, CX-nek a C-ből induló belső szögfelezőre vonatkozó tükörképe rendre az AX', BX', CX' egyenes.
 

14. feladat. Igazoljuk, hogy a két Brocard-pont talpponti háromszöge hasonló az ABC háromszöghöz.
 

15. feladat. Igazoljuk, hogy a két Brocard-pont éppen az X(bc:ca:ab) és az X'(cb:ac:bc).
 

16. feladat. A 4. tételben egy transzformációt adtunk meg, amely minden X ponthoz, ha az nem illeszkedik a háromszög oldalegyeneseire, egy X0 pontot rendel. Igazoljuk, hogy ha X az X(x:y:z) pont, akkor X0 az X0(1a2x:1b2y:1c2z) pont!
 

*

 

Ez után a kitérő után az L pontnak egy újabb tulajdonságát mutatjuk be. Láttuk, hogy a súlypont és az L pont között szoros összefüggés van (vö. a 17. és a 22. tételt). A mostani tétel az L pontot a Gergonne-ponttal hozza kapcsolatba.
 

25. tétel. Tegyük fel, hogy az ABC háromszög nem derékszögű. Körülírt körének az A, B, C pontban húzott érintői egy olyan PQR háromszöget alkotnak, amelynek Gergonne-pontja megegyezik az ABC háromszög Lemoine‐Grebe-pontjával.
 
 
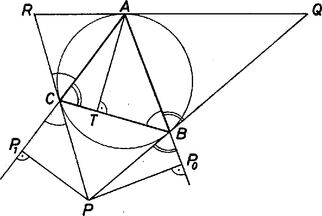10. ábra
 

A bizonyításban egyelőre feltesszük, hogy az ABC háromszög hegyesszögű. Legyen a B-ben és C-ben húzott érintő metszéspontja P, a C-ben és A-ban húzott érintőké R, az A-ban és B-ben húzottaké Q (10. ábra). A PQR háromszög Gergonne-pontja a PA, RB, QC egyenesek metszéspontja. A tétel bizonyításához tehát azt kell belátni, hogy PA, RB, QC az ABC háromszög szimmediánjai, hiszen ezek metszéspontja éppen az ABC háromszög Lemoine‐Grebe-pontja. Nyilván elég ezt a PA egyenesről belátni. A 23. tétel szerint pedig ehhez elég, hogy valamely A-tól különböző pontjának távolsága az AB és AC oldaltól AB:AC arányú. Válasszuk ezt a pontot P-nek. Azt kell igazolnunk, hogy PP0:PP1=AB:AC, ahol P0 és P1 a P vetülete az AB, ill. az AC oldalon.
Tudjuk, hogy PCP1∢=RCA∢=ABC∢ (a kerületi és érintőszög egyenlősége alapján), s hasonlóan PBP0∢=ABQ∢=ACB∢. Legyen A vetülete BC-n a T pont. Ekkor CAT és BPP0 valamint BAT és CPP1 hasonló háromszögek, mert két-két szögük megegyezik. Az előbbiből CA:AT=BP:PP0, az utóbbiból BA:AT=CP:PP1. Ezek hányadosa
CA:BA=(BP:CP):(PP1:PP0).
Itt BP és CP közös pontból húzott érintő szakaszok, tehát CA:BA=PP1:PP0, amiből a kívánt állítás átrendezéssel következik.
 

*

 

17. feladat. Igazoljuk, hogy ha A-nál derékszög van, akkor az A-n átmenő szimmedián párhuzamos a B és C-ben húzott érintőkkel!
 

18. feladat. Döntsük el, hogy jó-e a fenti bizonyítás, ha A-nál tompaszög van. Hogyan módosul a bizonyítás, ha B-nél (vagy C-nél) van tompaszög?
 

19. feladat. A k körhöz a külső P pontból meghúzzuk az érintőket, az érintési pontok X és Y. A k kör egy további pontja Z. Igazoljuk, hogy a PZ egyenes az XY szakaszt XZ2:YZ2 arányban osztja.
 

*

 

A Gergonne-pont és a Lemoine-pont között van még egy érdekes összefüggés. Legyen a hegyesszögű ABC háromszög A-ból, B-ből, C-ből induló magasságának talppontja a szemben levő oldalon rendre T, U, V. Az UV szakasz antiparalel BC-vel, tehát az A-ból induló ta szimmedián felezi UV-t (21. tétel).
 
 
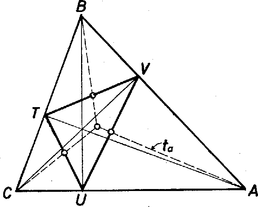11. ábra
 

Ismert, hogy a TUV háromszög hozzáírt köreinek középpontja rendre A,B és C, hiszen a magasságok felezik az UVT háromszög szögeit, ezért az AB, BC, CA egyenesek az UVT háromszög külső szögfelezői (11. ábra). Az ABC háromszög ta szimmediánja tehát azonos a TUV háromszög UV oldalához írt kör középpontját az UV oldal felezőpontjával összekötő egyenessel. A 10. tétel szerint ez az egyenes átmegy a TUV háromszög középvonal háromszögének Gergonne-pontján. Beláttuk tehát az alábbi tételt:
 

26. tétel. A hegyesszögű ABC háromszög szimmediánjai átmennek a magaságponthoz tartozó talpponti háromszög középvonalháromszögének Gergonne-pontján. Az ABC háromszög Lemoine‐Grebe-pontja tehát a magasságponthoz tartozó talpponti háromszög középvonalháromszögének Gergonne-pontja.
 

Érdekes eredményre jutunk, ha a 25. és 26. tételt összevetjük. Ha XYZ nem derékszögű háromszög, akkor a 25. tétel szerint beírt körének érintési pontjai olyan X'Y'Z' háromszöget alkotnak, amelynek Lemoine-pontja az XYZ háromszög Gergonne-pontjával egyezik meg. Másrészt az X'Y'Z' háromszög talpponti háromszögének középvonal-háromszöge olyan, hogy Gergonne-pontja megint csak megegyezik az X'Y'Z' háromszög Lemoine-pontjával. Ha ebből az utoljára kapott háromszögből megint képezzük a beírt körének érintési pontjai által alkotott háromszöget, ennek a háromszögnek a Lemoine‐Grebe-pontja azonos lesz az X'Y'Z' háromszög Lemoine‐Grebe-pontjával.
Hogy kapott eredményünket egyszerűbben kifejezhessük, bevezetjük a következő jelöléseket. Az XYZ háromszög beírt körének érintési pontjai által alkotott háromszöget eXYZ jelöli, az XYZ háromszög középvonalháromszögét kXYZ, az XYZ háromszög magasságtalppontjai alkotta háromszögét pedig tXYZ. A magasságtalppontok alkotta háromszög középvonalháromszöge tehát ktXYZ. A 26. tétel ezzel a jelöléssel így fogalmazható: ktXYZ háromszög Gergonne-pontja azonos XYZ háromszög Lemoine-pontjával. A fentebb megfogalmazott követelmények pedig így szólnak: a kteXYZ és XYZ háromszögek Gergonne-pontja, valamint az ektXYZ és az XYZ háromszögek Lemoine-pontja azonos.
Megjegyezzük, hogy ektXYZ és kteXYZ oldalai párhuzamosak az XYZ háromszög megfelelő oldalaival, és XYZ-t egy-egy L, ill. G középpontú tükrözve kicsinyítés viszi át az ektXYZ, ill. kteXYZ háromszögbe.
 

*

 

20. feladat. Bizonyítsuk be ezt az utóbbi állítást! Igazoljuk, hogy a kicsinyítés aránya az előbbi esetben 2cosαcosβcosγ, az utóbbi esetben ϱ/4r.
 

21. feladat. Bizonyítsuk be, hogy az XYZ háromszöget az etkXYZ, tkeXYZ, ketXYZ háromszögbe rendre egy-egy K, O, M közepű tükrözve kicsinyítés viszi. A kicsinyítés aránya rendre 2cosαcosβcosγ, ϱ/4r, 2cosαcosβcosγ.
 

22. feladat. Nevezzük az XYZ háromszög kotangens-pontjának (ctg-pontjának) azt a pontot, melynek az YZ, ZX, XY oldalaktól vett távolsága úgy aránylik egymáshoz, mint ctgα2:ctgβ2:ctgγ2. Igazoljuk, hogy az XYZ háromszöget a tekXYZ háromszögbe a ctg-pontra vonatkozó ϱ/4r arányú tükrözve kicsinyítés viszi.
A 20‐22. feladatok állításai természetesen csak akkor igazak, ha a háromszögek hegyesszögűek!
 

23. feladat. Fogalmazzuk meg a 26. tétel megfelelőjét arra az esetre, mikor az ABC háromszög tompaszögű!

*


A 20. feladat szerint az ektABC háromszög az ABC háromszögből L középpontú, ‐ 2cosαcosβcosγ arányú kicsinyítéssel jön létre. A Lemoine‐Grebe -pontnak egy további szép tulajdonsága, hogy könnyen jellemezhetők azok a háromszögek, amelyek az ABC háromszögből L középpontú, nyújtással, kicsinyítéssel jönnek létre.
 

27. tétel. Írjunk az ABC háromszög oldalaira olyan, egymáshoz hasonló ABB0A0, BCC1B1, CAA2C2 téglalapot, amelyben AB:BB0=BC:CC1==CA:AA2=1:λ. (Ha λ>0, akkor a téglalapok "kifelé'', ha λ<0, akkor a téglalapok "befelé'' állnak. |λ|=1 esetén a téglalapok négyzetek.) Tekintsük az A0B0, B1C1, C2A2 egyenesek határolta (az ABC háromszöghöz hasonló) háromszöget. Ez a háromszög az ABC háromszögnek L-ből nyújtott (kicsinyített) képe.
 
 
12. ábra
 

A bizonyításhoz legyen C2A2 és A0B0 egyenesek metszéspontja P, A0B0 és B1C1 metszéspontja Q, B1C1 és A2C2 metszéspontja R (12. ábra). Legyen továbbá P vetülete az AB, AC egyenesen P0 és P1. PP0BB0 téglalap, tehát PP0=BB0=λ⋅AB. Ugyanígy PP1=λ⋅AC, tehát PP0:PP1=AB:AC. A 23. tétel szerint tehát P rajta van az ABC háromszög ta szimmediánján, vagyis PA egybeesik ta-val. Hasonlóan QB a tb, RC pedig a tc szimmedián, s mivel az ABC háromszög a PQR háromszög nagyított (kicsinyített) képe, ez a három egyenes egy pontban, a hasonlósági centrumban metszi egymást. (Ezzel újabb bizonyítást is adtunk arra, hogy a három szimmedián egy pontban metszi egymást.) A hasonlóság centruma tehát valóban az L pont.
 

*

 

24. feladat. Igazoljuk, hogy a PQR háromszögből az ABC háromszög
λ+12(ctgα+ctgβ+ctgγ)


arányú kicsinyítéssel (nyújtással) jön létre!
 

25. feladat. Igazoljuk, hogy minden, az ABC háromszögből L közepű nyújtással vagy kicsinyítéssel keletkező háromszög megkapható a 27. tétel eljárásával!
 

*

Befejezésül az L pontnak két további tulajdonságát mutatjuk be. Az első egy szélsőérték problémával kapcsolatos. Legyen X az ABC háromszög síkjának tetszőleges pontja, legyen X távolsága a BC, CA, AB oldalaktól rendre x, y, z. Nyilvánvaló, hogy x+y+z akármilyen nagy negatív értéket felvehet, viszont |x|+|y|+|z| a háromszögnek a leghosszabb oldallal szemközti csúcsában minimális.
 

*

 

26. feladat. Igazoljuk ezeket az állításokat!
 

*

 

Nehezebb feladat annak az X pontnak a meghatározása, amelyre x2+y2+z2 minimális.
 

28. tétel. Ha az X pont távolsága az ABC háromszög három oldalától x, y, z, akkor
x2+y2+z2≥4t2a2+b2+c2.


Egyenlőség akkor és csak akkor áll, ha X=L.
 

A bizonyításhoz gondoljuk meg, hogy ax+by+cz=2t (a távolságok előjelesek, ezért ez a sík minden X pontjára igaz). Másrészt
(a2+b2+c2)(x2+y2+z2)=(ax+by+cz)2++(ay-bx)2+(az-cx)2+(bz-cy)2(≥ax+by+cz)2=4t2.


Egyenlőség akkor és csak akkor áll, ha ay=bx, az=cx, bz=cy, azaz x:y:z=a:b:c, tehát X a Lemoine‐Grebe-pont.
 

*

Hasonló ötlettel oldható meg az alábbi feladat:
 

27. feladat. A BC oldalegyenes tetszőleges X pontjának távolsága az AB és az AC oldalaktól y és z. Igazoljuk, hogy y2+z2 arra a pontra minimális, amelyben a ta szimmedián metszi a BC oldalt.
 

*

 

Megjegyezzük, hogy sok az x, y, z távolságokkal kapcsolatos érdekes egyenlőtlenség található Sklarszkij-Csencov-Jaglom: Válogatott feladatok és tételek az elemi matematika köréből 2/2. Geometriai egyenlőtlenségek és szélsőértékek. 107‐117. feladatai között.
 

Kanyarodjunk vissza a 16. tételhez. Ott beláttuk, hogy az L ponton keresztül húzott három antiparalel az oldalakból egy kör hat pontját metszi ki. Belátjuk, hogy ugyanez a párhuzamosokra is igaz:
 

29. tétel. Az a hat pont, amit az L ponton keresztül az oldalakkal húzott párhuzamosak metszenek ki a másik két oldalból, egy körön van.
 
 
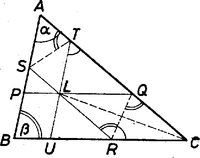13. ábra
 

Legyen a három párhuzamos a 13. ábra jelölésével PQ, RS és TU. Az LQCR paralelogramma átlói felezik egymást, tehát CL felezi a QR szakaszt. A CL szimmediánról tudjuk, hogy felezi az AB oldallal antiparalel szakaszokat, így a Q-ból induló QR' antiparalelt is. Belátjuk, hogy R=R'. Ha ugyanis R≠R' volna, a QR és QR' szakaszok felezőpontjait összekötő szakasz párhuzamos volna RR'-vel, tehát BC-vel, és nem lehetne mindkét felezőpont a CL egyenesen. Ezért R=R', és a QR szakasz antiparalel az AB oldallal. Hasonlóan TS antiparalel a BC oldallal. Ezért CRQ∢=CAB∢=α és CQR∢=β=ATS∢. Másrészt a párhuzamosságok miatt QTU∢=α és SRQ∢=RQC∢=β.
Azt kaptuk, hogy a TQRS négyszög R-nél fekvő szöge egyenlő a T-nél fekvő külső szöggel, valamint hogy a TURQ négyszög T-nél fekvő belső szöge egyenlő az R-nél levő külső szögével. Ezért mindkét négyszög húrnégyszög, vagyis a QRT háromszög köré írt körön rajta van S is, U is. Ugyanezért az URQ háromszög köré írt körön (amely ugyanez a kör) rajta van a P pont is, a hat pont tehát valóban egy körön van.
 

*

 

28. feladat. Igazoljuk, hogy a QRL és az ABC háromszögek hasonlók.
 

29. feladat. Igazoljuk, hogy a ta szimmedián a BC oldalt b2:c2 arányban osztja.
 

30. feladat. Igazoljuk, hogy UR:RC:BU=a2:b2:c2.
 

31. feladat. Legyen az ABC háromszög A csúcsából induló magasságának talppontja T, a B-ből induló magasságáé U. Igazoljuk, hogy a C-ből induló súlyvonal a TU szakaszt a2:b2 arányban osztja.
 

32. feladat. Az ABC háromszög C csúcsánál derékszög van. A C-ből induló magasság F felezőpontját tükrözzük az A-ból induló belső szögfelezőre. A kapott F' pontot összekötjük A-val. Igazoljuk, hogy az AF' egyenes felezi a BC szakaszt!
 

33. feladat. Igazoljuk, hogy az ABC háromszög Lemoine‐Grebe-féle pontjának talpponti háromszögében az oldalak úgy aránylanak egymáshoz, mint az ABC háromszög súlyvonalai!
 

*

 

Ha visszapillantva áttekintjük az egy csúcsból, pl. A-ból induló transzverzálisokat, azt találjuk, hogy az AB oldalegyenes, az ma magasság egyenese, a ta szimmedián, az fα szögfelező, az sa súlyvonal, a köré írt K közepét A-val összekötő ra(=AK) sugár egyenese és végül az AC oldal hét olyan egyenes, amelyek ebben a sorrendben tükrösen helyezkednek el a szögfelezőre (az első az utolsónak tükörképe stb.). Az oldalakhoz tartozó "nevezetes pontok'' a háromszög csúcsai; a magasságok metszéspontja az M magasságpont; a szimmediánoké az L Lemoine-pont; a szögfelezőké a beírt kör O közepe; a súlyvonalaké az S súlypont; a sugaraké a körülírt kör K közepe. Látjuk tehát, hogy L természetesen illeszkedik bele az M, O, S, K nevezetes pontok közé ötödikként, s "szimmetrikussá'' teszi azokat.
A Lemoine‐Grebe-pontnak valóban számos szép tulajdonságát sikerült felfedeznünk. Ezeket most mind összefoglaljuk.
 

A magasságok felezőpontját a szemközti oldal felezőpontjával összekötő három szakasz egy L pontban találkozik (12. tétel).
 

Egyetlen olyan L pont van az ABC háromszög síkjában, amely egyszerre közepe a három oldal fölé írt egy-egy téglalapnak. A sík bármely más pontja legföljebb egy oldal fölé írt téglalapnak lehet középpontja (14. tétel).
 

Egyetlen olyan L pont van ABC síkjában, amely felezi mindhárom, rajta átmenő antiparalel szakaszt. E három szakasz egyenlő hosszú, s végpontjai egy L közepű körön vannak. Bármely két szakasz négy végpontja valamelyik oldal fölé írt téglalapot alkot (16. tétel).
 

Az ABC háromszög síkjában pontosan egy olyan L pont van, amely súlypontja a saját talpponti háromszögének (17. tétel).
 

Ha az ABC háromszögbe beírt PQR háromszög oldalainak négyzetösszege minimális, akkor a PQR háromszög egy L pont talpponti háromszöge (20. tétel).
 

A háromszög szimmediánjai egy L pontban találkoznak (22. tétel).
 

Az ABC háromszög síkjának egyetlen olyan L pontja van, amelynek a BC, CA, AB oldalaktól vett távolsága BC:CA:AB arányú (24. tétel).
 

Legyen az X pont előjeles távolsága a három oldaltól x, y, z. Az x2+y2+z2 négyzetösszeg a sík egyetlen L pontjára minimális, x2+y2+z2≥4t2/(a2+b2+c2), és egyenlőség csak erre az L pontra áll (28. tétel).
 

Ha az ABC háromszög oldalaira egymással hasonló (és azonos) körüljárású ABB0A0, BCC1B1, CAA2C2 téglalapokat írunk, akkor a B0A0, C1B1, A2C2 egyenesek által alkotott háromszög (mely hasonló az ABC háromszöghöz ) az ABC háromszögnek mindig ugyanabból az L pontból nagyított (kicsinyített) képe (27. tétel).
 

E kilenc tulajdonság bármelyike ugyanezt a pontot, a háromszög Lemoine‐Grebe-féle pontját definiálja. Ennek a pontnak további nevezetes tulajdonságai:
 

L-en keresztül a három oldallal húzott párhuzamos az oldalakat hat pontban metszi, ez a hat pont egy körön van (29. tétel).
 

Ha az ABC nem derékszögű háromszög, akkor van olyan PQR háromszög, amelynek beírt vagy valamelyik hozzáírt köre a QR, RP, PQ oldalakat rendre A, B, C-ben metszi. A PQR háromszög Gergonne-pontja az ABC háromszög Lemoine-pontja (25. tétel).
 

Ha az ABC háromszög hegyesszögű, akkor Lemoine-pontja megegyezik a magasság talpponti háromszögének középvonal-háromszögében a Gergonne-ponttal. Ha ennek a középvonalháromszögnek a beírt köre az oldalait A', B', C' pontokban metszi, akkor az A'B'C' háromszög Lemoine‐Grebe-pontja azonos az ABC háromszög Lemoine‐Grebe-pontjával, s az A'B'C' háromszög egy L középpontú, tükrözve kicsinyítéssel kapható az ABC háromszögből (26. tétel).
*Ezzel a kérdéssel foglalkozott az 1955. évi Országos Középiskolai Tanulmányi Verseny II. 3. feladata. Lásd: Molnár Emil: Matematikai Versenyfeladatok Gyűjteménye, 74. oldal, 182. feladat.