Kezdőlap


Cím:	A háromszög kevésbé ismert nevezetes pontjairól I. rész
Szerző(k):	Surányi László
Füzet:	1984/október, 289 - 294. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Nagel-pont

A címet elolvasva rögtön felmerül a kérdés: a háromszög mely pontjait nevezzük nevezetes pontnak? Nemrégiben a KÖMAL-ban (64. kötet, 4. szám, 1982. ápr.) is megjelent egy érdekes cikk, amely ezt a kérdést tárgyalta (Hermann Bauer: Hány nevezetes pontja legyen a háromszögnek ?). Eszerint a háromszög négy nevezetes pontja a magasságpont, a súlypont, továbbá a háromszög beírható és köré írható körének közepe. Megmutatja, hogy az oldalfelező pontokból alkotott középvonal-háromszög beírt körének közepe szintén sok szép tulajdonsággal rendelkezik, és bizonyos szempontból természetesen egészíti ki tulajdonságaival az említett négy pontot.
Nyilván részben ízlés kérdése, hogy melyik pontot nevezzük "nevezetes pontnak''. Német (és magyar) geométerek általában az elsőnek felsorolt négy pontot tekintik nevezetesnek. Ennek részben fizikai, részben történeti okai vannak: vizsgálatukat ókori görög matematikusok kezdték el.
Jelen cikkben főleg francia geométerek (Lemoine és Gergonne) nyomán kevésbé ismert nevezetes pontokra szeretnénk felhívni a figyelmet. Ezek nem definiálhatók olyan egyszerűen, mint pl. a beírt kör középpontja, ám olyan sok meglepő és szép tulajdonságuk van, hogy nem csoda, ha egy matematikus az egyik ilyen pontot a magasságpont, a súlypont és beírt kör középpontja mellett a háromszög negyedik legfontosabb pontjának nevezte.

\begin{matrix} * \end{matrix}

1. A beírt kör közepe a szögfelezők találkozási pontja, a magasságpont a magasságoké, a súlypont pedig a súlyvonalaké. Definiálásukhoz mindhárom esetben előbb be kell bizonyítani, hogy a megfelelő egyenesek valóban egy pontban találkoznak. (A köré írt kör közepe ‐ s az említett cikk által javasolt ötödik nevezetes pont, a középvonal háromszög beírt körének közepe ‐ ebből a szempontból kicsit rendhagyó: a középvonal-háromszög magasságainak, ill. szögfelezőinek metszéspontja. Ezek is három-három egyenesnek a metszéspontjai.)
Az

A B C

háromszög Ceva-szakaszának vagy a háromszög transzverzálisának azt a szakaszt (egyenest) nevezzük, ami a háromszög egyik csúcsát a szemközti oldal valamely pontjával köti össze. A nevezetes pontok vizsgálata az alábbi, G. Ceva (1678‐1734) olasz matematikustól származó tétellel kezdődik:

1. tétel (Ceva tétele) Legyen

D

E

F

B C

C A

A B

oldalak egy-egy pontja. Az

A D

B E

C F

Ceva-szakaszok pontosan akkor találkoznak egy pontban, ha

\begin{matrix} B D \cdot C E \cdot A F = D C \cdot E A \cdot F B . \end{matrix}

(A tétel bizonyítása megtalálható pl. Coxeter és Greitzer: Az újra felfedezett geometria c. könyvének 19‐20. oldalán; egy másik bizonyítás található Horvay és Reiman: Geometriai feladatok gyűjteménye I. kötetében, az 1263‐64. feladat megoldásában.)

Ez a tétel máris módot ad két újabb nevezetes pont definiálására:

2. tétel. Érintse az

A B C

háromszög beírt köre a

B C

C A

A B

oldalakat rendre a

D

E

F

pontban. Az

A D

B E

C F

Ceva-szakaszok egy pontban találkoznak. Ezt a pontot nevezzük a háromszög Gergonne-pontjának (1. ábra).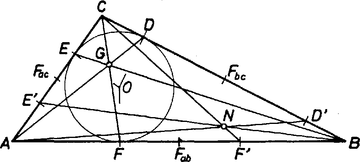

1. ábra

3. tétel. Ha az

A B C

háromszög

A B

B C

C A

oldalához irt kör a megfelelő oldalt rendre az

F'

D'

E'

pontban érinti, akkor az

A D'

B E'

C F'

Ceva-szakaszok egy pontban találkoznak. Ez a pont a háromszög Nagel-pontja.

A 2. tétel bizonyításához elég emlékeztetnünk arra, hogy egy pontból a körhöz húzott érintőszakaszok egyenlőek, ezért

B D = B F

A F = A E

és

C E = C D

. Következésképp

B D \cdot C E \cdot A F = D C \cdot E A \cdot F B

, és így Ceva tétele szerint

A D

B E

C F

valóban egy pontban találkozik.
A továbbiakban az

A B

B C

C A

oldalak felezőpontját

F_{a b}

F_{b c}

F_{c a}

-val fogjuk jelölni, s általában az

X Y

szakasz felezőpontját

F_{x y}

nal. A 3. tétel bizonyításához elég azt meggondolni, hogy

D

-nek

F_{b c}

-re vonatkozó tükörképe éppen

D'

, s ugyanígy

E'

E

-nek

F_{a c}

-re,

F'

pedig

F

-nek

F_{a b}

-re vonatkozó tükörképe. Következésképp

B D' = C D

C D' = B D

C E' = A E

A E' = C E

A F' = B F

és

B F' = A F

, tehát

\begin{matrix} B D' \cdot C E' \cdot A F' = C D \cdot A E \cdot B F, \end{matrix}

\begin{matrix} C D' \cdot A E' \cdot B F' = B D \cdot C E \cdot A F . \end{matrix}

A jobb oldalon álló szakaszok páronként egyenlők, egyenlők tehát a bal oldalon álló szorzatok értékei is, ezért Ceva tétele szerint az

A D'

B E'

C F'

Ceva-szakaszok valóban egy pontban találkoznak.

A 3. tétel. bizonyításánál tulajdonképpen csak annyit használtunk fel, hogy a jobb oldali szorzatok egyenlők, vagyis az

A D

B E

C F

szakaszok egy pontban találkoznak.

Így tehát a következő tételt igazoltuk.

4. tétel. Legyen

D

E

F

B C

C A

A B

oldal egy-egy pontja, e három pontnak a megfelelő oldal felezőpontjára vonatkozó tükörképe pedig

D'

E'

F'

. Az

A D

B E

C F

szakaszok akkor és csak akkor találkoznak egy

K

pontban, ha az

A D'

B E'

C F'

is egy

K'

pontban találkoznak.
A 4. tétel tehát a háromszög minden "nevezetes pontjához'' hozzárendel egy másikat. A súlyponthoz önmagát rendeli, a Gergonne-ponthoz a Nagel-pontot és viszont. Általában ha

K

-hoz

K'

-t rendeli, akkor

K'

-hoz

K

-t. Érdemes elgondolkozni azon, mit rendel a magasságponthoz, a körülírt és a beírt kör közepéhez!

Mind a régi, mind az új nevezetes pontokat úgy definiáltuk, hogy előbb létezésüket bizonyítottuk. A matematika nem leíró tudomány, már legegyszerűbb definíciói mögött is sokszor mély, észre sem vett gondolati munka van. Problémák, feladatok megoldása sokszor egy gondosan megadott definíción múlik, ezt a jelen cikkben is látni fogjuk.

\begin{matrix} * \end{matrix}

2. Most rátérünk a Nagel-pont vizsgálatára.
A továbbiakban rögzítünk egy (tetszőleges)

A B C

háromszöget. Ennek Gergonne-pontját

G

-vel, Nagel-pontját

N

-nel, a beírt kör és a

B C

C A

A B

oldalak érintési pontját rendre

D

E

F

-fel, ezek

F_{b c}

F_{c a}

, ill.

F_{a b}

-re való tükörképét rendre

D'

E'

F'

-vel jelöljük. (

G

tehát az

A D

B E

C F

N

pedig az

A D'

B E'

C F'

szakaszok közös pontja.) A szokásos jelöléssel

B C = a

C A = b

A B = c

, a velük szemben fekvő szögek a háromszögben

α

β

γ

s = \frac{a + b + c}{2}

ϱ

A B C

háromszög beírt körének sugara,

r

a körülírt körnek;

ϱ_{a}

ϱ_{b}

ϱ_{c}

pedig az

a

b

, ill.

c

oldalhoz hozzáírt körök sugara.

5. tétel. Az

A B C

háromszög

S

súlypontja,

N

Nagel-pontja és beírt körének

O

közepe egy egyenesen van és

O S : S N = 1 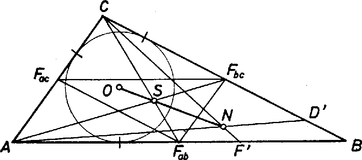: 2

(2. ábra).

2. ábra

Az 5. tétel (melyet érdemes összevetni a bevezetőben idézett cikk 3. tételével) az alábbi tétellel egyenértékű:

6. tétel.Az

A B C

háromszög beírt körének közepe az oldalfelező pontokból alkotott középvonal-háromszög Nagel-pontja.

Ismeretes, hogy az

A B C

háromszög oldalfelező pontjai által alkotott háromszöget az

A B C

háromszög

S

súlypontjából

(- 2) : 1

arányú nagyítás éppen az

A B C

háromszögbe viszi át, hiszen a súlyvonalak harmadolják egymást. Az 5. tétel azt mondja ki, hogy ennél a transzformációnál az

A B C

háromszög beírt körének

O

középpontja a Nagel-pontba megy át. A hasonlósági transzformáció a középvonal-háromszög Nagel-pontját az

A B C

háromszög Nagel-pontjába viszi, amivel a két tétel ekvivalenciáját beláttuk.
Elég tehát a 6. tételt bizonyítani. Erre többfajta számolásos bizonyítás ismeretes. Az alábbi, ha nem is a leggyorsabb, de a háromszög több geometriai tulajdonságára mutat rá.

3. ábra

Érintse az

A F_{a b} F_{a c}

háromszög beírt köre az

F_{a b} F_{a c}

oldalt (3. ábra) a

D_{0}

pontban. Az

A F_{a b} F_{a c}

háromszög az

A B C

háromszögnek

A

-ból 1/2 arányban zsugorított képe, tehát az

A D_{0}

egyenes éppen

D

-ben metszi a

B C

oldalt és

D_{0}

felezi az

A D

szakaszt, továbbá

F_{a b} D_{0} = B D / 2

és

F_{a c} D_{0} = C D / 2

.
Érintse az

F_{a b} F_{a c} F_{b c}

háromszög beírt köre az

F_{a c} F_{a b}

oldalt

D_{1}

-ben. Az

F_{a b} F_{a c} F_{b c}

háromszög az

A B C

-nek az

S

súlypontból

- 1 / 2

arányban zsugorított képe (

B

-nek

F_{a c}

C

-nek

F_{a b}

felel meg). Ezért

F_{a c} D_{1} = B D / 2

. Azt kaptuk, hogy

F_{a b} D_{0} = F_{a c} D_{1}

, tehát

D_{0}

és

D_{1}

szimmetrikusak az

F_{a b} F_{a c}

oldal felezőpontjára. Minthogy

D

és

D'

tükrösek

B C

felezőpontjára, és az

S

súlypontból 1/2 arányban kicsinyítve

B

D

C

rendre

F_{a c}

D_{1}

F_{a b}

-be megy, ezért

D'

képe

D_{0}

lesz,

A D'

képe pedig

F_{b c} D_{0}

.
Jelölje a

B F_{b c} F_{a b}

háromszögbe beírt kör és az

F_{b c} F_{a b}

oldalnak az érintési pontját

E_{0}

, a

C F_{b c} F_{a c}

háromszögbe beírt kör és az

F_{b c} F_{a c}

oldal érintési pontját

F_{0}

. A fenti gondolatmenet elismétlésével azt kapjuk, hogy ha

S

-ből az

A B C

háromszöget

- 1 / 2

arányban kicsinyítjük,

B E'

képe

F_{a c} E_{0}

C F'

képe

F_{a b} F_{0}

lesz. A középvonal-háromszög Nagel-pontja tehát az

F_{b c} D_{0}

F_{a c} E_{0}

F_{a b} F_{0}

szakaszok közös pontja. Ha belátjuk, hogy az

A B C

háromszög beírt körének közepe mindhárom szakaszon rajta van, akkor a 6. tételt bizonyítottuk.
Nyilván elég azt belátni, hogy például az

A B C

háromszög beírt körének

O

közepe az

F_{b c} D_{0}

szakaszon van.

D_{0}

felezőpontja

A D

-nek, tehát

2 \vec{O D_{0}} = \vec{O A} + \vec{O D}

. Ugyanígy

2 \vec{O F_{b c}} = \vec{O B} + \vec{O C}

. Azt kell belátni, hogy

\vec{O D_{0}}

és

\vec{O F_{b c}}

párhuzamos. Ez akkor és csak akkor teljesül, ha a két vektor vektoriális szorzata nulla. Fejtsük ki a vektoriális szorzatukat!

\begin{matrix} (\vec{O A} + \vec{O D}) \times (\vec{O B} + \vec{O C}) = \vec{O A} \times \vec{O B} + \vec{O A} \times \vec{O C} + \vec{O D} \times \vec{O B} + \vec{O D} \times \vec{O C} . \end{matrix}

A jobb oldalon az

A B C

síkra merőleges vektorok állnak, hosszuk megegyezik az

O A B

O A C

O D B

O D C

háromszögek (előjeles) területével, közülük az első és az utolsó a sík egyik oldalára, a másik kettő a sík másik oldalára mutat a háromszögek körüljárási irányának megfelelően. A négy vektor összege tehát akkor nulla, ha

\begin{matrix} t_{O A B} + t_{O D C} = t_{O A C} + t_{O D B} . \end{matrix}

Nyilvánvaló, hogy

\begin{matrix} t_{O A B} + t_{O D C} = \frac{1}{2} (A B + D C) ϱ és t_{O A C} + t_{O D B} = \frac{1}{2} (A C + D B) ϱ . \end{matrix}

A B + D C = s = A C + D B

, a kívánt egyenlőség tehát fennáll. Ezzel az 5. és 6. tétel bizonyítását befejeztük.
Az az állítás, hogy

D_{0}

O

F_{b c}

egy egyenesbe esik, speciális esete Newton alábbi nevezetes tételének:

7. tétel. A

P Q R S

érintőnégyszög átlóinak felezőpontját összekötő egyenes átmegy a beírt kör középpontján.

A mi esetünkben a

P Q R S

négyszög szerepét az

A B C D

"érintőnégyszög'' játszotta, melynek

B

D

C

csúcsai egy egyenesbe esnek. Az általános eset pontosan ugyanígy bizonyítható, a bizonyítás végén azt kell kihasználni, hogy érintőnégyszög két-két szemben levő oldalának összege egyenlő. [A Sklarszkij‐Csencov‐Jaglom: Válogatott feladatok az elemi matematika köréből Geometria/1 kötetének 135. a) feladata egy másik bizonyítást ad Newton tételére, pusztán területátalakításokkal. A fenti bizonyítás is elmondható volna területátalakításokkal, de vektorokkal lényegesen rövidebb és elegánsabb.]

8. tétel. Az

N

Nagel-pontra

A N : A D' = a : s

A 6. tétel bizonyításánál használt jelölésekkel

A N : A D' = F_{b c} O : F_{b c} D_{0}

, mert

S

-ből

- 1 / 2

arányban kicsinyítve

A

N

D'

képe rendre

F_{b c}

O

és

D_{0}

. Másrészt

F_{b c} O : F_{b c} D_{0} = ϱ : \frac{m_{a}}{2}

, hiszen

O

távolsága a

B C

oldaltól

ϱ

D_{0}

távolsága pedig

\frac{m_{a}}{2}

. De

ϱ : \frac{m_{a}}{2} = 2 ϱ : m_{a} = a : s

, hiszen

2 ϱ s = 2 t_{A B C} = a m_{a}

9. tétel. A Nagel-pont távolsága a

B C

C A

A B

oldaltól rendre

2 ϱ \frac{s - a}{a}

2 ϱ \frac{s - b}{b}

2 ϱ \frac{s - c}{c}

vagy másképp

ϱ \frac{m_{a}}{ϱ_{a}}

ϱ \frac{m_{b}}{ϱ_{b}}

ϱ \frac{m_{c}}{ϱ_{c}}

F_{a b} F_{a c} F_{b c}

háromszög Nagel-pontja

O

O

távolsága

F_{a b} F_{a c}

-tól

\frac{m_{a}}{2} - ϱ

N

távolsága

B C

-től (az

S

-ből történő

- 2 : 1

arányú nagyítás miatt) ennek kétszerese, vagyis

m_{a} - 2 ϱ

. De

a m_{a} = 2 ϱ s

, tehát

m_{a} = \frac{2 ϱ s}{a}

, ezért

m_{a} - 2 ϱ = 2 ϱ \frac{s - a}{a}

, ahogy állítottuk.
Végül

a m_{a} = 2 t_{A B C} = 2 ϱ_{a} (s - a)

, ahonnan

2 ϱ \frac{s - a}{a} = ϱ \frac{m_{a}}{ϱ a}

\begin{matrix} * \end{matrix}

1. feladat. Igazoljuk, hogy a Nagel-pontnak a

B C

C A

A B

oldaltól mért távolságai úgy aránylanak egymáshoz, mint

\frac{1}{1 - cos α} : \frac{1}{1 - cos β} : \frac{1}{1 - cos γ}

2. feladat. Igazoljuk, hogy a Gergonne-pontnak a

B C

C A

A B

oldaltól mért távolságai úgy aránylanak egymáshoz, mint

\frac{1}{1 + cos α} : \frac{1}{1 + cos β} : \frac{1}{1 + cos γ}

3. feladat. Az

A B C

háromszög

A B

oldalához írt kör érintse az

A B

oldalt

F'

-ben, az

A C

oldalt

E_{2}

-ben. Az

A C

oldalhoz írt kör érintse az

A C

oldalt

E'

-ben.

B E'

és

C F'

egyenesek metszéspontján keresztül húzzunk párhuzamost

A C

-vel, az

A

csúcson keresztül pedig

B E'

-vel. Bizonyítsuk be, hogy ez a két egyenes az

F' E_{2}

egyenesen metszi egymást.

\begin{matrix} * \end{matrix}

Befejezésül térjünk még vissza egy rövid időre a 7. tételre, és alkalmazzuk azt pl. az

A B D' C

"érintőnégyszögre''. Valóban, ez is érintőnégyszög, ahogy az

A B D C

négyszög az

A B C

háromszög beírt köre köré írt érintőnégyszög, ugyanígy az

A B D' C

B C

oldalhoz hozzáírt kör érintőnégyszöge. Jelölje most

O_{1}

a hozzá írt körnek középpontját. Azt állítjuk, hogy

B C

oldalfelező pontját

A D'

szakasz felezőpontjával összekötő egyenes átmegy

O_{1}

-en. A 6. tétel bizonyítása során használt gondolatmenet szerint ehhez megint csak annyit kell belátni, hogy az

\begin{matrix} (\vec{O_{1} A} + \vec{O_{1} D'}) \times (\vec{O_{1} B} + \vec{O_{1} C}) = \vec{O_{1} A} \times \vec{O_{1} B} + \vec{O_{1} D'} \times \vec{O_{1} B} + \vec{O_{1} A} \times \vec{O_{1} C} + \\ + \vec{O_{1} D} \times \vec{O_{1} C} . \end{matrix}

kifejezés értéke a nullavektor. A jobb oldalon az

A B C

háromszög síkjára merőleges vektorok állnak, hosszuk rendre

t_{O_{1} A B}

t_{O_{1} D' B}

t_{O_{1} A C}

t_{O_{1} D' C}

. A háromszögek körüljárásának megfelelően az első két vektor azonos féltérbe, a másik kettő a másik féltérbe mutat. Annyit kell tehát belátni, hogy

t_{O_{1} A B} + t_{O_{1} D' B} = t_{O_{1} A C} + t_{O_{1} D' C}

. De ez igaz, hiszen

\begin{matrix} t_{O_{1} A B} + t_{O_{1} D' B} = (A B + D' B) ϱ_{a} = s \cdot ϱ_{a} = (A C + D' C) ϱ_{a} = t_{O_{1} A C} + t_{O_{1} D' C} . \end{matrix}

Azt kaptuk, hogy az

A D'

szakasz felezőpontját

B C

oldalfelezőpontjával (

F_{b c}

-vel) összekötő egyenes átmegy a

B C

oldalhoz hozzáírt kör középpontján. A 6. tétel bizonyítása során láttuk, hogy

A D'

felezőpontja éppen

D_{1}

, vagyis a középponti háromszög beírt körének érintési pontja (l. 3. ábra). Az

A D'

felezőpontját

F_{b c}

-vel összekötő szakaszon tehát rajta van a középponti háromszög Gergonne-pontja! A következő tételhez jutottunk tehát:

10. tétel. Az

A B C

háromszög oldalaihoz írt körök középpontját a megfelelő oldal felezőpontjával összekötő egyenesek a középvonalháromszög Gergonne-pontjában találkoznak.

Ennek a tételnek ‐ amelyet a 6. tétellel való rokonsága miatt bizonyítottunk ‐ teljes jelentősége csak a következő részben fog kiderülni (l. a 26. tételt).

\begin{matrix} * \end{matrix}

4. feladat. Szerkesszünk háromszöget, ha ismerjük két oldalának különbségét, a harmadik oldalhoz tartozó magasságát, s az ehhez az oldalhoz írt kör sugarát!