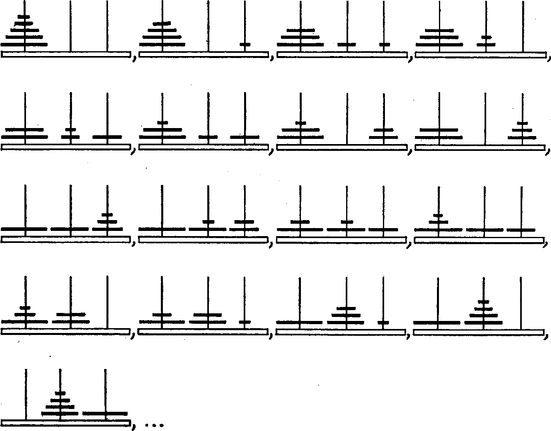Cím: Egy sorozat és a "Hanoi tornyai"
Szerző(k):  Fried Kati 
Füzet: 1984/április, 151 - 155. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bináris (2-es számrendszerbeli) számláláskor úgy növelünk 1-gyel, hogy jobbról indulva az 1-eseket 0-ra váltjuk egészen addig, amíg 0-hoz nem érünk, amit átírunk 1-esre. Pl.

10111+1=11000,101+1=110,10+1=11.

Kezdjük a számlálást 0-tól és minden szám mellé írjuk fel, hogy hátulról számítva hányadik értéken cseréltünk 0-t 1-esre (an), illetve azt, hogy ez a helyi érték 2 hányadik hatványát jelöli (bn):
 
n  0)  1    10   11  100  101  110  111 1000...an  1  2131214)bn  0  1020103)
 


Látható, hogy a bn sorozat elemei 1-gyel kisebbek, mint az an-ek. Az an sorozat képzési szabályát így fogalmazhatjuk meg:
 

MMMM   az első elemtől kezdve minden második  1-es,MMMM   a második elemtől kezdve minden negyedik  2-es,  MMMM   a negyedik elemtől kezdve, minden nyolcadik  3-as,

MMMMMMMMMMMMMMMMMMM.MMMMMMMMMMMMMMMMMMM.MMMMMMMMMMMMMMMMMMM.a  2k-adik elemtől kezdve minden  2k+1-edik (k+1)-es.  

 

A bn sorozatnál tehát a 2k-adik elemtől kezdve minden 2k+l-edik k-as.
A hatványok sorozata egyúttal azt az információt is megadja, hogy n kettes számrendszerbeli alakja hány 0-ra végződik. Ez oszthatóságra átfogalmazva azzal egyenértékű, hogy 2bn|n, de 2bn+1∤n; Ezt úgy mondják, hogy 2bn pontos osztója n-nek és így jelölik: 2bn∥n; (Ezzel analóg a 10-es számrendszerben az, hogy egy számnak 10 annyiadik hatványa a pontos osztója, ahány nullára végződik a szám.)
Ha 2a∥n és 2b∥m, akkor 2a+b∥n⋅m (gondoljunk arra, hogy hány 0-ra végződik n, m és n⋅m). Ebből a bn sorozat egy érdekes tulajdonsága adódik:
bn⋅m=bn+bm.
Ezt a tulajdonságot additivitásnak nevezik. Ilyen tulajdonságú pl. a logaritmus függvény is:
lg(n⋅m)=lgn+lgm.
Az 1, 2, 1, 3, 1, 2, 1, 4, ... sorozatnak sok érdekes tulajdonsága van.
Előfordulhat, hogy végtelen sok sorozatot akarunk "összefésülni'', azaz az elemeket egy sorozatba egyesíteni. Jelöljük az elemeket xi,j-vel, ahol az első index arra utal, hogy hányadik sorozatban van az elem, a második pedig arra, hogy ezen belül hányadik helyen; xi,j az i-edik sorozat j-edik eleme.
 

x1,1x1,2→x1,3x1,4→...↓↗↙↗↙x2,1x2,2x2,3x2,4...↙↗↙x3,1x3,2x3,3x3,4...↓↗↙↗x4,1x4,2x4,3x4,4...⋮↙

 


Az
x1,1,x2,1,x1,2,x1,3,x2,2,x3,1,x4,1,...
fölsorolást háromszögszerűnek nevezhetnénk, az
x1,1,x2,1,x2,2,x1,2,x1,3,x2,3,x3,3,x3,2,x3,1,...
fölsorolást négyszögszerűnek.
 

x1,1x1,2→x1,3x1,4→...↓↑↓↑x2,1→x2,2x2,3x2,4...↓↑x3,1↤x3,2↤x3,3x3,4...↓↑x4,1→x4,2→x4,3→x4,4...⋮

 

Azt a felsorolást pedig, amelynek n-edik tagja az an-edik sor legkisebb, a felsorolásban még nem szereplő tagja, nevezhetjük például logaritmikusnak:
x1,1,x2,1,x1,2,x3,1,x1,3,x2,2,x1,4,x4,1,...
Egy másik érdekes tulajdonsága a sorozatunknak, hogy kapcsolatba hozható a Hanoi tornyai néven ismert játékkal, amely a következő. Egy rúdon egyre kisebbedő korongok vannak. Úgy kell a korongokat egy másik rúd segítségével egyesével egy harmadikra átrakni, hogy egyszer se kerüljön kisebb korongra nagyobb. A megoldások közül természetesen a lehető legrövidebb érdekel minket. Ezt legkönnyebben rekurzióval lehet elmondani. Egy korong esetén világos, hogy mi a teendő, n≥2 korong esetén (n-1)-et áthelyezünk a második rúdra, az n-ediket a harmadik rúdra, majd az (n-1)-et a második rúdról átrakjuk a harmadikra.
Ebből két dolgot láthatunk:
1.n korong áthelyezéséhez 2n-1 lépés elegendő;
2.páratlan számú koronggal indulva elsőként a harmadik rúdra, páros számú koronggal indulva elsőként a második rúdra kell tennünk.
A rekurziót és a két állítást az alábbi ábra illusztrálja n=5 korong esetén. A korongokat felülről lefelé számozzuk meg. Ha fölírjuk, hogy hányadik korongot mozgatjuk, akkor újra az an sorozatot kapjuk: 1, 2, 1, 3, 1, 2, 1, 4, ...
 
 

Rendeljük hozzá a korongokhoz a megfelelő (bináris) helyiértéket, a lépésszámhoz annak bináris alakját. Az alábbi táblázat az ábra alapján készült, a felső ötjegyű szám a lépésszámot mutatja kettes számrendszerben (megfelelő számú nullát eléírva), alatta pedig az egyes helyiértékeken aszerint áll 1, 2 vagy 3, hogy az ötödik, negyedik stb. korong melyik oszlopon áll.
 


Lépésszám)0000000001000100001100100001010011000111Korongok)1111111113111231112211322113211133111333

 


Lépésszám)0100001001010100101101100011010111001111Korongok)1233312332123121231112211122131222312222
 

Megfigyelhetjük, hogy ha az egymás alatt levő ötjegyű számokat egyforma számjegyekből álló blokkokra bontjuk, azok határai egybeesnek; továbbá ha egy, a korongok elhelyezkedését leíró számot veszünk ki, ott egy blokkot átölelő blokkban egyforma számjegyek állnak, ha középen páros sok jegy van (pl. amikor a lépésszám 01100, a "22''-es blokkot "1'', illetve "11'' blokk veszi körül); és ezek a számjegyek különbözők, ha a blokkban páratlan sok számjegy van.
Ezek a törvényszerűségek nemcsak itt, hanem általában is igazak. Ahhoz tehát, hogy a lépésszámból meghatározhassuk, hol is helyezkednek el a korongok, mindössze az első két blokkról kell tudnunk, hogy 1, 2, 3 közül melyik áll benne.
Az első blokk csak 1-es és 3-as lehet ‐ hiszen a legnagyobb korong más rúdra nem kerül: amíg a lépésszám bináris alakja 0-val kezdődik, addig az első, utána pedig a harmadik rúdon van. A második blokk pedig kettesekből áll, ha az első blokkban páratlan sok elem volt, egyébként pedig 3-as vagy 1-es.
Nem kell külön "kiokoskodnunk'' ezeket a számokat, ha a következőket csináljuk:
 

1. felírjuk k bináris alakját n jegyűre kiegészítve, majd elé 011-et írunk;
2. a számban az első 0 alá 1-et, az ezt követő 1-esek alá 3-at írunk, egészen addig, míg a számban egy 0-hoz nem érünk;
3. ha egy egyező számjegyekből álló blokk alá már odaírtuk az 1, 2, 3 valamelyikét, akkor az ezután következő blokk jegyei alá aszerint kerül az a szám, amely a megelőző blokk előtt szerepelt vagy az 1, 2, 3 közül a harmadik, hogy az előző blokkban páros sok vagy páratlan sok számjegy van-e.
 

Így például ha 20 korongot teszünk át az elsőről a harmadik rúdra, ekkor a leírtak alapján 220-1= 1048575 lépés kell. A 275419-edik lépésben a korongok elhelyezkedése
 

  0    1 1    0 1 0 0 0 0    1 1 0 0    1 1 1 1 0 1 1    0    1 1    1    3 3    1 2 3 3 3 3    2 2 3 3    2 2 2 2 3 1 1    3    2 2  

 


ugyanez a félmilliomodik lépésben (500000=11110100001001000002)
 

  0 1 1    0 1 1 1 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0    1 3 3    1 2 2 2 2 1 3 2 2 2 2 3 1 1 3 2 2 2 2 2  

 


és az egymilliomodikban:
 

  0 1 1    1 1 1 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0    1 3 3    3 3 3 3 1 2 3 3 3 3 2 1 1 2 3 3 3 3 3 3  

 

Próbáljuk meghatározni, hogy az itt látható két ábra a 20 korong átrakásának hányadik lépéseit ábrázolja.
 
 
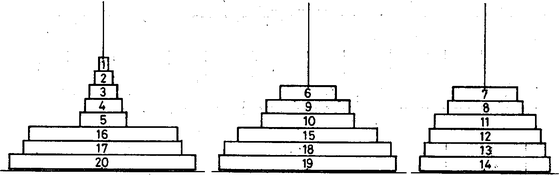1. ábra
 

 
 
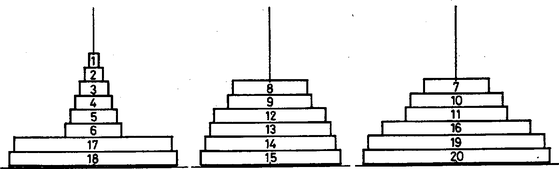2. ábra
 

(Megoldás: a 154. oldal 1. ábráján a 410400. lépés, a második ábrán annak kétszerese látható.)