Cím: Paraboláról, hiperboláról elemi geometriai eszközökkel I. rész
Szerző(k):  Rácz János 
Füzet: 1984/április, 145 - 150. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész

 

Néhány bevezető tétel

 

1. TÉTEL. Ha van négy egyenes, amely négy háromszöget alkot, akkor a háromszögek körülírt köreinek van közös pontja.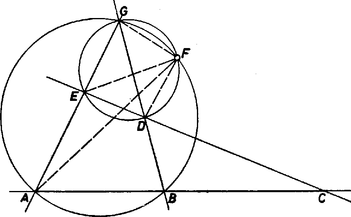
 
 
1. ábra
 

Bizonyítás. Az 1. ábra 4 egyenese az ABG, EDG, AEC, BDC háromszögeket határozza meg. Először megrajzoltuk az ABG és DEG háromszögek körülírt köreit. E két körnek G közös pontja. Ha G volna az egyetlen közös pont, akkor a két kör egymást G-ben érintené, így G lenne e két kör külső hasonlósági pontja, tehát ED és AB párhuzamos lenne, ellentétben a feltétellel. Így a két körnek G-n kívül van még egy közös pontja, F. Megmutatjuk, hogy F rajta van az AEC és BDC háromszögek körülírt körén is: FEC∢=FED∢=FGD∢=FGB∢=FAB∢=FAC∢. Így A rajta van FC szakasz FEC szögű látókörén. FDC szög az FGED húrnégyszög külső szöge, FBC szög pedig az FGAB húrnégyszög külső szöge, tehát FGE∢=FGA∢=FDC∢=FBC∢; így D és B rajta van az FC szakasz FGE szögű látókörén.
⋆

 

Adott az ABC háromszög és síkjában a P pont. Legyen A1 a BC, B1 az AC, C1 az AB egyenesnek az a pontja, amelyre PB1C∢=PA1C∢=PC1A∢=φ (2. ábra).
 
 
2. ábra
 

2. TÉTEL. A B1, C1, A1 pontok akkor és csakis akkor kollineárisak, ha P rajta van ABC háromszög körülírt körén.
 

Bizonyítás. A feltétel miatt PCB1A1 és PBA1C1 is húrnégyszög. Ezért B1CP∢+PA1B1∢=180∘; PA1C1∢=PBC1∢. Ha B1A1C1∢=180∘, akkor
PCA∢=PA1C1∢=PBC1∢, tehát PCAB húrnégyszög. ‐ Ha viszont PCAB húrnégyszög, akkor PCB1∢=PBC1∢=PA1C1∢, tehát PA1B1∢+C1A1P∢=180∘, tehát B1, A1, C1 kollineáris.
⋆

A 3. ábrán egy tetszőleges ABC hegyesszögű háromszög látható és egy ugyancsak tetszőleges g egyenes, amelyik a háromszög mindhárom oldalegyenesét metszi. A g egyenesnek a BC, CA, AB oldalegyenesekre vonatkozó tengelyes tükörképei rendre a ga, gb, gc egyenesek. Legyen A¯ a gb és gc, továbbá B¯ a gc és ga, végül C¯ a ga és gb metszéspontja. Az ábrával kapcsolatban néhány tételt mondunk ki és bizonyítunk be.
 
 
3. ábra
 

3. TÉTEL. Az ABC¯ háromszög hasonló az ABC háromszög talpponti háromszögéhez és vele ellentétes körül járású.
 

Bizonyítás. A gc tekinthető a ga egyenesnek először a BC, majd a BA egyenesre vonatkozó tengelyes tükörképének. De két tengelyes tükrözés szorzata a metszéspont körüli, a tengelyek szögének kétszeresével történő forgatást jelent, tehát QaBA¯∢=2CBA∢ (ahol Qa a g és ga egyenesek metszéspontja), tehát ABC¯∢=180∘-2β. Innen a tétel könnyen adódik.
 

4. TÉTEL. A BB¯, CC¯, AA¯ egyenesek az ABC¯ háromszög belső szögfelezői.
 

Bizonyítás. Ha a B pontot mint a ga egyenes pontját tekintjük, akkor a fenti két tengelyes tükrözés szorzata B¯-t az E pontba viszi, így B¯BE∢=2β; vagyis ‐ ha BD merőleges gc-re ‐, akkor B¯BD∢=β. Így DB¯B∢=90∘-β; tehát BB¯ valóban szögfelezője az ABC¯ szögnek.
 

5. TÉTEL. Az ABC¯ háromszög beírt körének O¯ középpontja rajta van az ABC háromszög körülírt körén.
 

Bizonyítás. A CO¯A szög kiegészítő szöge a CBO¯∢=90∘-β-nak, ezért CO¯A∢=β; így az ABO¯C négyszög valóban húrnégyszög.
Ha egy a g-vel párhuzamos h egyenesnek tekintjük a BC, CA, AB oldal-egyenesre vonatkozó tengelyes tükörképeit, akkor e tükörképek párhuzamosak lesznek g megfelelő tükörképeivel, így a BhChAh háromszög középpontosan hasonló a BAC¯ háromszöghöz. A BD egyenes hc-re is merőleges lesz, ezért a BBh és BB¯ egyenesek egybeesnek. A párhuzamos egyenesek által létrehozott háromszögek közös beírt középpontja 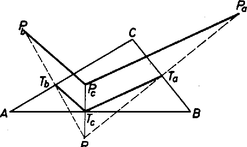O¯.
 
 
4. ábra
 

Kézenfekvő a kérdés: vannak-e olyan egyenesek, amelyeknek egy háromszög oldalegyeneseire vonatkozó tengelyes tükörképei egy ponton mennek keresztül? A 4. ábrán látható P pont akkor lehet a három tüköregyenes metszéspontja, ha P-nek a három oldalegyenesre vonatkozó tengelyes tükörképei: Pa, Pb, Pc kollineárisak. De Pa, Pb, Pc akkor és csak akkor kollineáris, ha Ta, Tb, Tc is az, ahol Ta, Tb, Tc a PPa, PPb, ill. PPc egyeneseknek a megfelelő oldalakkal való metszéspontjai, hiszen PbPa∥TbTa, PaPc∥TaTc. De a Ta, Tb, Tc pontok a 2. tétel alapján akkor és csakis akkor kollineárisak, ha P rajta van ABC háromszög körülírt körén (most φ=90∘).
 

6. TÉTEL. A körülírt kör minden P pontjához tartozik pontosan egy olyan g egyenes, amelynek az oldalakra vonatkozó tengelyes tükörképei: ga, gb, gc átmennek a P ponton.
 

Bizonyítás. P-nek az oldalegyenesekre vonatkozó Pa, Pb, Pc, tükörképei egyértelműen meghatározottak, így pontosan egy ilyen egyenes létezik.
 

7. TÉTEL. A P körülírt köri ponthoz a 6. tételben megjelölt g egyenes átmegy a háromszög M magasságpontján.
 

Bizonyítás. Elég megmutatni, hogy Qb, M és Qc kollineárisak. AMQbMb deltoid, tehát QbMbA∢=AMQb∢; MAMcQc szintén deltoid, tehát AMcQc∢=QcMA∢; de MbAMcP a feltétel szerint húrnégyszög, így QbMbA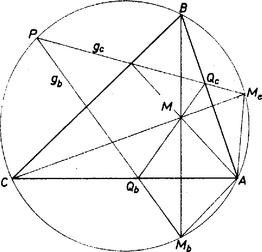∢+AMcQc∢=180∘=AMQb∢+QcMA∢ (5. ábra).
 
 
5. ábra
 

8. TÉTEL. Minden a magasságponton átmenő h egyeneshez tartozik a körülírt körnek pontosan egy pontja úgy, hogy h-nak az oldalegyenesekre vonatkozó tengelyes tükörképei átmennek ezen a ponton (6. ábra).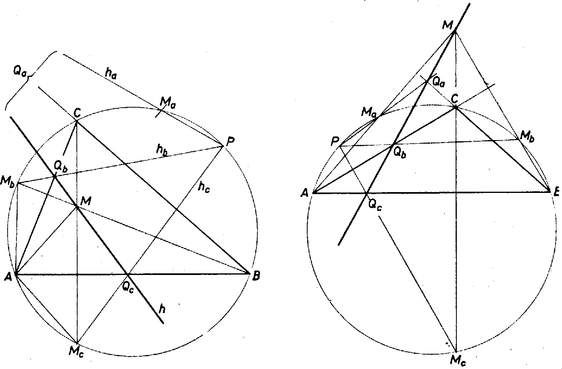
 
 
6. ábra
 

Bizonyítás. Az előbbi deltoidok most is megvannak, most AMQb∢+QcMA∢=180∘=QbMbA∢+AMcQc∢; így MbAMcP valóban húrnégyszög.
 

9. TÉTEL. Ha négy egyenes négy háromszöget alkot, akkor a négy magasságpont egy egyenesen van.
 

Bizonyítás. Legyen az 1. ábra GED háromszögének magasságpontja M1, a GAB háromszögé M2, a CAE háromszögé M3, a DBC háromszögé M4. Tekintsük az M1M2 egyenest. Legyen a 8. tétel alapján az M1M2 egyeneshez tartozó körülírt köri pont F. De az M1M3, illetve M1M4 egyenesekhez is F tartozik. A 6. tétel alapján azonban F-hez pontosan egy egyenes tartozhat, így a négy magasságpont egy egyenesen van.
⋆

Az 1. ábra AE szakaszát át akarjuk vinni ugyanezen ábra BD szakaszába, úgy, hogy az A pont B-be, az E pedig D helyére kerüljön. Legyen M a sík tetszőleges pontja. Forgassuk el M körül AGB szöggel az AE szakaszt. Elforgatottja az A1E1 szakasz. Ez ugyanolyan hosszú, mint AE és párhuzamos BD-vel. Legyen N az A1B és E1D egyenesek metszéspontja. Ekkor az N középpontú, BD:AE arányú középpontos hasonlóság A1E1-et BD-be viszi. ‐ Természetesen lehet először a középpontos hasonlóságot alkalmazni: M hasonlósági középpont és BD:AE arány az AE szakaszt a vele párhuzamos A2E2 szakaszba viszi úgy, hogy A2E2 és BD egyenlő hosszúságú szakaszok. Legyen L az A2B felező merőlegesének és E2D felező merőlegesének metszéspontja. Most L körüli, AGB szögű forgatás A2-t B-be, E2-t D-be viszi. Nyilván L és N két különböző pont. Így tehát minden (M) forgásközépponthoz szerkeszthető egy (N) hasonlósági középpont; és minden (M) hasonlósági középponthoz szerkeszthető egy (L) forgásközéppont úgy, hogy az első esetben egy AGB szögű forgatás és egy BD:AE arányú középpontos hasonlóság, a második esetben egy BD:AE arányú középpontos hasonlóság és egy AGB szögű forgatás szorzataként az AE szakasz a BD szakaszba megy át.
Kézenfekvő a kérdés: van-e a síkon olyan Q pont, amelyik nemcsak forgásközéppont, hanem hasonlósági középpont is, illetve olyan R pont, amely nemcsak hasonlósági középpont, hanem forgásközéppont is.
 

10. TÉTEL. Egy hasonlósági transzformációnak legfeljebb egy fix pontja lehet.
 

Bizonyítás. Tegyük fel, hogy van két fix pont: Q és R. Ekkor a QR szakasz képe is QR, így ebben az esetben az arány 1 és nem az előre megállapított.
Ha tehát sikerül olyan pontot találni, amely egyszerre forgásközéppont és hasonlósági középpont mindkét sorrendben, akkor megtaláltuk a keresett Q, illetve R pontot.
 

11. TÉTEL. Az 1. ábra F pontja egyszerre forgásközéppont és hasonlósági középpont mindkét sorrendben.
 

Bizonyítás. a) AGD∢=EFD∢=AFB∢. Tehát az F körüli, AGD szögű forgatás az E pontot az FD egyenesre, E3 pontjába viszi, az A pontot pedig az FB egyenesére az A3 pontba. Így a forgatás után A3E3=AE és A3E3∥BD. Az A3B és E3D egyenesek metszéspontja éppen F, így az F középpontú, BD:A3E3=BD:AE arányú középpontos hasonlóság AE-t BD-be viszi.
b) Alkalmazzunk először egy F középpontú, BD:AE arányú középpontos hasonlóságot AE-re. Ez az A pontot az FA egyenes A4 pontjába, az E pontot az FE egyenes E4 pontjába viszi úgy, hogy A4E4=BD és A4E4∥AE. Így az F körüli, AGD szögű forgás E4-et a D, az A4-et pedig a B pontba viszi.
F tehát annak a forgatva-nyújtásnak a középpontja, amely az AE szakaszt a BD szakaszba viszi.
 

1. feladat. Mutassuk meg, hogy F annak a forgatva-nyújtásnak is középpontja, amelyik az AB szakaszt az ED szakaszba viszi.
 

2. feladat. Mutassuk meg, hogy ha AB párhuzamos ED-vel, akkor G annak a forgatva-nyújtásnak a középpontja, amelyik AE-t BD-be viszi.
 

3. feladat. Szerkesztendő négyszög, ha adott négy oldala és két szemben fekvő szögének összege.
 

4. feladat. Igazoljuk, hogy egy négyszögben a szemben fekvő oldalak szorzatának összege nem kisebb, mint az átlók szorzata. Igazoljuk, hogy egyenlőség akkor és csakis akkor áll fenn, ha a négyszög húrnégyszög.
⋆

Osztóviszony, ideális elemek

 

Legyen A, B, C három, egy egyenesen levő pont, ekkor az (ABC) osztóviszony az AC→:CB→ arányt jelenti. Vektorok osztását általában nem értelmezhetjük, de egyállású vektorok arányát igen, hiszen ezek egymásnak számszorosai. Az osztóviszony értelmezéséből következik, hogy az osztóviszony pozitív, ha C az AB szakaszon van, mégpedig az osztóviszony szigorúan monoton nő, ha C tart B felé. Az osztóviszony a B-n túli félegyenesen negatív, B környezetében alulról nem korlátos, a félegyenes minden pontjában (-1)-nél kisebb. Az A-n túli félegyenesen mindenütt -1 és 0 között van. Ha C bármelyik félegyenesen "elég távol'' van, akkor a -1 előre meghatározott környezetébe esik az osztóviszony. Ezért célszerű az egyenest egy i d e á l i s  p o n t t a l kiegészíteni úgy, hogy az egyenes ideális pontjára legyen az osztóviszony értéke -1. Párhuzamos egyenesekhez közös ideális pontot célszerű rendelni, és így a sík bármilyen két egyenesének lesz pontosan egy közös pontja. Különböző állású egyenesekhez különböző ideális pontot rendelünk. (Ellenkező esetben ugyanis két különböző állású egyenesnek két közös pontja lenne: metszéspontjuk és ideális pontjuk.)
Két különböző ideális ponthoz az őket összekötő egyenest kell rendelnünk. Ennek az egyenesnek közönséges pontja nem lehet, mert egy közönséges pont és egy ideális pont meghatároz egy közönséges egyenest, közönséges egyeneshez pedig pontosan egy ideális pontot rendeltünk. Két ideális pontot összekötő egyenesnek minden pontja ideális pont, így ez az egyenes i d e á l i s  e g y e n e s.
A síkhoz egyetlen ideális egyenest célszerű rendelni. Ha ugyanis volna olyan ideális pont, amelyik nincs rajta az ideális egyenesen, akkor ez a pont és az ideális egyenes egy rögzített pontja meghatározna egy második ideális egyenest, és ekkor volna olyan közönséges egyenes, amelyik mindkét ideális egyenest metszené, tehát volna közönséges egyenes két ideális ponttal.