Cím: Egy olimpiai feladat általánosítása (1984. március)
Szerző(k):  Hetyei Gábor 
Füzet: 1984/március, 102 - 107. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1983. évi diákolimpia negyedik feladata a következő volt.

 
Legyen ABC egyenlő oldalú háromszög! Álljon az E halmaz az AB, BC és CA zárt szakaszok összes pontjából! Igaz-e, hogy bármilyen módon osztjuk is fel E-t két diszjunkt részhalmazra, ezeknek a részhalmazoknak legalább egyikében mindig van három olyan pont, amelyek egy derékszögű háromszög csúcspontjai?
 
A továbbiakban ennek a feladatnak néhány általánosításáról lesz szó. Megvizsgáljuk, hogy milyen háromszögek kerületére létezik a feladat feltételeinek megfelelő két részhalmazra osztás, majd foglalkozunk néhány olyan esettel, amikor E nem egy háromszög, hanem valamilyen más síkidom kerületének pontjaiból áll. Az említett két részhalmazra osztás színezéssel tehető szemléletessé: az egyik részhalmaz pontjait fessük piros, a másik részhalmaz pontjait pedig kék színűre. Nevezzük az E halmaz egy színezését jónak, ha nincs olyan derékszögű háromszög, melynek csúcsai egyszínű E-beli pontok lennének.
 
1. Tétel: Hegyesszögű háromszög kerületének nincsen jó színezése.
 
Elsőként megmutatjuk, hogy ha az ABC háromszög kerületét sikerült jól színezni, akkor az AB oldalra legalább két piros pont esik. Állításunkat indirekt módon láthatjuk be. Tegyük fel ugyanis, hogy az AB szakasz pontjai a P pont kivételével kékek. A P pontról nem tudjuk, hogy kék vagy piros. Ekkor az AC és BC szakaszok bármely pontjának AB-n vett merőleges vetülete - ABC hegyesszögű lévén - az AB szakasz belsejébe vagy határára esik. Vegyük az AC vagy BC szakasz egy tetszőleges, A-tól és B-től különböző R pontját. Ha R' ennek a pontnak az AB-re eső merőleges vetülete, és R' nem azonos P-vel, akkor R csak piros lehet, mert ellenkező esetben R, R' és az AB szakasz még egy tetszőleges kék pontja egy egyszínű derékszögű háromszög csúcsai lennének. Tehát ekkor AC és CB pirosak, kivéve esetleg azt az egyetlen Q pontot, melynek merőleges vetülete P. (Q színét szintén nem ismerjük.) Feltehető, hogy Q pl. a BC oldalra illeszkedik (lehet Q=C is), BC egy tetszőleges, Q-tól különböző X belső pontját véve, X piros; AC-re eső merőleges vetülete, amit Y-nal jelölünk, szintén piros, Y az AC oldal belső pontja és AC egy tetszőleges, Y-tól különböző Z belső pontja szintén piros, ugyanakkor YXZ háromszög derékszögű. Ellentmondásra jutottunk, tehát az AB oldalon csakugyan van legalább két piros pont.
 
 

Hasonló módon bármely oldalról beláthatjuk, hogy van rajta legalább két piros, ill. legalább két kék pont. Ebből könnyen adódik, hogy jó színezés esetén a kerület egy pontja, és valamely oldalra eső merőleges vetülete különböző színűek.
 
 

Tegyük fel ugyanis, hogy pl. mind P, mind az AB-re eső Q merőleges vetülete piros. Az előbb bizonyítottak szerint AB-n legalább két piros pont van, létezik tehát Q-tól különböző R piros pont is, ugyanakkor PQR derékszögű háromszög, és így ellentmondásra jutottunk.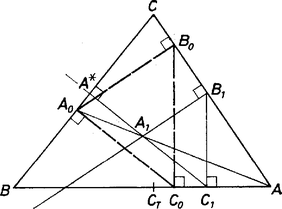
 
 

Ezután megmutatjuk, hogyan lehet olyan A0B0C0 háromszöget szerkeszteni, melyre A0, B0, C0 az ABC háromszög kerületének pontjai, A0B0⊥AC, B0C0⊥AB és A0C0⊥BC. Legyen CT a C-hez tartozó magasságtalppont, és vegyük az ACT szakasz tetszőleges C1 belső pontját. A C1-ben az AB-re állított merőleges messe AC-t a B1-ben, C1 merőleges vetülete BC-n legyen A*, B1-ben AC-re állított merőleges messe a C1A* egyenest A1-ben. Az A1B1C1 háromszög rendelkezik a megkívánt merőlegességi tulajdonságokkal, csak A1 nem feltétlenül illeszkedik BC-re. Legyen AA1 és BC metszéspontja A0. Az A középpontú, AA0AA1 arányú nagyítás A1B1C1 háromszöget éppen a kívánt tulajdonságú A0B0C0 háromszögbe viszi.
Tegyük fel, hogy ABC hegyesszögű háromszög kerületének van jó színezése. Tekintsük az így meghatározott A0, B0, C0 pontokat. A fentiek szerint A0, B0 és C0 színe páronként különböző, hiszen e pontok egymás merőleges vetületei. Ugyanakkor csak két színünk van, így A0, B0 és C0 színe közül legalább kettő megegyezik. Ellentmondásra jutottunk, tehát csakugyan nem létezhet jó színezés.
Mivel a szabályos háromszög is hegyesszögű, így az említett diákolimpiai feladat kérdésére adott válasz nemleges.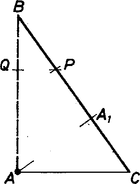
 
2. Tétel: Derékszögű háromszög kerületének nincs jó színezése.
 
Legyen az ABC háromszögben a derékszög A-nál, és tegyük fel, hogy a háromszögnek mégis van jó színezése.
 
 


Feltehető, hogy A kék. Ha mindkét befogón lenne A-tól különböző kék pont, akkor ezek A-val együtt egy derékszögű háromszög egyszínű csúcsai lennének. Tehát a két befogó egyikén ‐ mondjuk AB-n ‐ nincs több kék pont, minden A-tól különböző pont piros. Ha BC átfogó valamely P belső pontja piros lenne, akkor AB-re eső Q merőleges vetülete és a B csúcs három olyan piros pont lenne, ami egyszínű derékszögű háromszöget határoz meg. Tehát BC minden belső pontja kék. Ekkor azonban A merőleges vetülete BC-n, A1 és BC még egy tetszőleges belső pontja egy derékszögű háromszög csúcsai, kékek. Ismét ellentmondásra jutottunk, a tételt bebizonyítottuk.
 

3. Tétel: Tompaszőgű háromszögnek van jó színezése.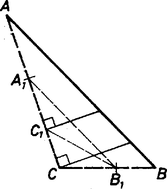
 
Színezzük például a leghosszabb oldalt kékre, a másik kettőt pirosra. Mivel az összes kék pont egy egyenesre esik, így kék csúcsú derékszögű háromszög szóba sem jöhet.
 
 


Válasszunk ki a piros pontok közül tetszőlegesen hármat, A1,B1,C1-et. Feltehető, hogy közülük kettő: A1 és C1 az AC oldalra esik és C1 van közelebb C-hez. Ha A1B1C1 derékszögű háromszög lenne, akkor B1 nem eshetne AC-re, így csak BC belső pontja lehetne. Mivel C-ben az AC-re állított merőleges az ACB szög belsejében halad, így B1 és A1C1 ennek az egyenesnek különböző oldalaira esnek. Emiatt A1 és B1 a C1-ben AC-re álltott merőlegesnek is különböző oldalaira esnek, azaz A1C1B1>90∘, így A1B1C1 háromszög nem lehet derékszögű. Tehát csakugyan jó a megadott színezés.
 

Most néhány más síkidom kerületének színezésével foglalkozunk.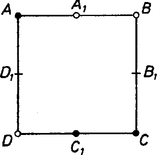
 
4. Tétel: Négyzet kerületének nincsen jó színezése.
 
Jelöljük a négyzet csúcsait A, B, C, D-vel. Ha ezek közül három egyszínű, akkor a színezés máris "rossz''. Tehát két piros és két kék pont van köztük. Ha a két piros és a két kék pont egy-egy oldal két végpontja, pl. A és D kék, B és C piros, akkor a DC oldal egy tetszőleges P pontja nem lehet sem kék (ADP háromszög miatt), sem piros (a BCP háromszög miatt). Tehát egy jó színezésben a két-két egyszínű csúcs csak átlósan helyezkedhet el.
 
 

 
 

Tekintsük az A1, B1, C1, D1 oldalfelező pontokat. A1 és C1 közül legalább az egyik piros, másképp A1C1C derékszögű háromszög csúcsai kékek lennének. Feltehető, hogy például A1 piros, ekkor az A1BC1 háromszögből C1 kék. Ekkor azonban B1 sem piros (A1BB1 háromszög miatt), sem kék (C1CB1 háromszög miatt) nem lehet. Ellentmondásra jutottunk, tehát a négyzetnek nincsen jó színezése.
 
5. Tétel: Kör kerületének van jó színezése.
 

Legyen például az AB átmérő A végpontja kék, B végpontja piros, az egyik AB félkör belső pontjai pirosak, a másik AB félköré kékek. Ekkor bármely átmérő egyik végpontja kék, a másik piros. Tetszőleges P, Q, R pontokat kiválasztva, ha PQR háromszög derékszögű, akkor Thalész tétele szerint valamelyik kettő, pl. P és Q, egy átmérő két végpontja, így különböző színű.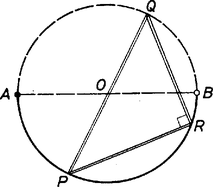
 
 

Érdekes módon ez a tétel szolgáltat alapötletet a következő tételhez:
 
6. Tétel: A szabályos 2n-szög kerületének nincs jó színezése.
 
n=2-re az állítást a 4. tétel mondja ki. n≧3 esetén megrajzoljuk a 2n-szög körülírt körét. Először belátjuk, hogy jó színezés esetén bármely kettő, egy átmérőn fekvő csúcsnak különböző színűnek kell lennie.
Tegyük fel ugyanis, hogy két egy átmérőn levő csúcs pl. piros. Thalesz tétele szerint bármely más csúcsot hozzávéve e két csúcshoz, derékszögű háromszöget kapunk. Így az összes többi csúcs kék, és így van olyan átmérő, melynek mindkét végpontja kék csúcs, továbbá ezen kívül is van kék csúcs (a kék csúcsok száma 2n-2≧2⋅3-2=4), így van olyan derékszögű háromszög, melynek mindhárom csúcsa kék, ami lehetetlen. Tehát csakugyan az egy átmérőn levő csúcsok különböző színűek. Mivel eszerint nem minden csúcs egyszínű, így van két szomszédos különböző színű csúcs, pl. A kék és B piros szomszédos csúcsok. Legyen A' az A tükörképe a körülírt kör O középpontjára, és B tükörképe O-ra B'. Ekkor A' piros és B' kék. Így az AB oldal tetszőleges P belső pontja nem lehet sem kék (PAB' háromszög miatt), sem piros (PA'B háromszög miatt). Tehát csakugyan nincsen jó színezés.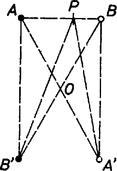
 
 

Végül bebizonyítjuk, hogy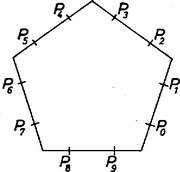
 
7. Tétel: Szabályos n-szög kerületének nincsen jó színezése.
 
Ha n páros, akkor állításunk a 6. tétel szerint igaz. Ha n páratlan, akkor vegyünk fel egy szabályos 2n-szöget, melynek csúcsai valamelyik körüljárási irány szerint P0, P1,...,P2n-1. A P0P1, P2P3,P4P5,...,P2n-2P2n-1 egyenesek egy szabályos n-szög oldalegyenesei, ezt a szabályos n-szöget megfelelő nagyítással átvihetjük bármely szabályos n-szögbe, így a színezhetőséget vizsgálhatjuk ezen a szabályos n-szögön is.
 
 

A konstrukció szerint a P2k és P2k+1 pontok (k=0,1,...,n-1) egy oldalon vannak. Az előbbi tételből látott módon - P0P1...P2n-1 körülírt körének megrajzolásával - belátható, hogy a Pk és Pk+n pontok különböző színűek (k+n>2n esetén Pk+n helyett Pk+n-2n értendő). Mivel eszerint az összes Pi pont nem lehet mind egyszínű, így van olyan i, hogy Pi és Pi+1 különböző színűek, mondjuk Pi piros, Pi+1 kék. Ekkor Pn+i kék és Pn+i+1 piros. Ha i páros, akkor Pi és Pi+1 egy oldalon vannak, ha i páratlan, akkor n+i páros, és így Pn+i és Pn+i+1 vannak egy oldalon. A szimmetria miatt feltehető, hogy i páros. Ekkor a PiPi+1 szakasz része az n-szög egy oldalának és tetszőleges Q belső pontja nem lehet sem kék (Pi+1QPn+i háromszög miatt), sem piros (PiQPn+i+1 háromszög miatt). Tehát a szabályos n-szög kerülete ez esetben sem lesz jól színezhető.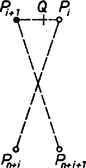
 
 

Megjegyezzük, hogy a 6. és 7. tételből egy újabb megoldás olvasható ki az eredeti olimpiai feladatra. A 4., 6. és 7. tételek bizonyításában lényegében egy erősebb állítást láttunk be: a 4. és a 6. tétel szerint már egy tetszőleges 2n-szög csúcsaiból és oldalfelező pontjaiból álló pont 4n-esnek sincs jó színezése (a bizonyításban belső pont az oldal felezőpontja is). A 7. tételben pedig beláttuk, hogy a páratlan oldalú szabályos n-szög kerületén felvehető 2n szög csúcsainak és az oldalfelező pontoknak sincsen jó színezése. n=3-ra ez azt jelenti, hogy már a szabályos háromszög oldalharmadoló és oldalfelező pontjaiból álló 9 elemű ponthalmaznak sincsen jó színezése. Ez általában is így van: egy alakzatnak akkor és csak akkor nincs jó színezése, ha van olyan véges része, amit nem lehet jól színezni.