Kezdőlap


Cím:	1982. évi Nemzetközi Matematikai Diákolimpia két feladatának megoldása
Szerző(k):	Csirmaz László , Megyesi Gábor
Füzet:	1984/január, 8 - 11. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feladat: Egy $A_{1} A_{2} A_{3}$ háromszög nem egyenlő szárú, oldalait jelöljük $a_{1}$ , $a_{2}$ , $a_{3}$ -mal ( $a_{1}$ fekszik $A_{1}$ -vel szemben). Minden $i$ -re $(i = 1,2,3)$ $M_{i}$ az $a_{i}$ oldal felezőpontja, $T_{i}$ az a pont, amelyben a beírt kör érinti $a_{i}$ -t és $S_{i}$ a $T_{i}$ pont tükörképe az $A_{i}$ -hez tartozó belső szögfelezőre nézve. Bizonyitsuk be, hogy az $M_{1} S_{1}$ , $M_{2} S_{2}$ , $M_{3} S_{3}$ egyenesek egy ponton mennek át.

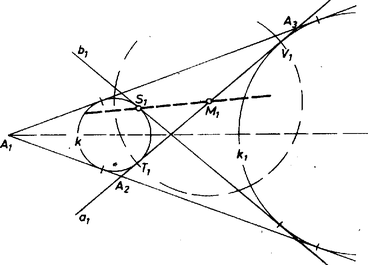
Megoldás. Az a feltétel, hogy a

A_{1} A_{2} A_{3}

háromszög nem egyenlő szárú, biztosítja, hogy a kérdéses egyenesek léteznek és különbözők. Tükrözzük a háromszög

a_{1}

oldalegyenesét az

A_{1}

csúcsból induló belső szögfelezőre. A kapott

b_{1}

egyenes érinti a

k

beírt kört, mégpedig

T_{1}

pont tükörképében, azaz

S_{1}

-ben, továbbá érinti a háromszög

a_{1}

-hez hozzáírt

k_{1}

körét is (1. ábra).

1. ábra

Tekintsük az

M_{1}

középpontú,

M_{1} T_{1} = M_{1} V_{1}

sugarú körre vonatkozó inverziót. Ez az inverzió helyben hagyja a

k

és

k_{1}

köröket, hiszen mindkettő merőleges az inverzió alapkörére: a

T_{1}

, illetve

V_{1}

metszéspontokból a középpontokba mutató sugarak merőlegesek egymásra. Állítjuk, hogy a

b_{1}

egyenes inverze éppen a háromszög Feuerbach-köre. Ebből a feladat állítása következik. Mivel

b_{1}

érinti

k

-t és

k_{1}

-et is, azért

b_{1}

inverze érinti

k

-nak, valamint

k_{1}

-nek inverzét, következésképp egy háromszög Feuerbach-köre érinti a háromszög beírt körét, továbbá a három hozzáírt kört is.
A beírt kör és a Feuerbach-kör érintési pontja inverz képe annak a pontnak, ahol

b_{1}

és

k

érinti egymást, vagyis az

S_{1}

pontnak, és így rajta van az

M_{1} S_{1}

egyenesen. Ugyanez az érintési pont rajta van az

M_{2} S_{2}

M_{3} S_{3}

egyeneseken is, s így

M_{1} S_{1}

M_{2} S_{2}

M_{3} S_{3}

valóban egy ponton mennek át, ahogyan a feladat állította.
Annak igazolása maradt még hátra, hogy

b_{1}

inverz képe a háromszög Feuerbach-köre. Mivel

b_{1}

nem megy át az inverzió középpontján,

M_{1}

-en (

a_{2} \neq a_{3}

miatt),

b_{1}

inverze egy

M_{1}

-en átmenő kör. S mivel az

A_{1} A_{2} A_{3}

háromszög Feuerbach-köre az

M_{1} M_{2} M_{3}

középháromszög körülírt köre, elegendő megmutatnunk, hogy

M_{2}

és

M_{3}

is rajta van

b_{1}

inverz képén, azaz

\begin{matrix} M_{1} X \cdot M_{1} M_{2} = M_{1} Y \cdot M_{1} M_{3} = M_{1} T_{1}^{2}, \end{matrix}

ahol

X

, ill.

Y

M_{1} M_{2}

, ill.

M_{1} M_{3}

félegyenesnek és a

b_{1}

-nek metszéspontjai (2. ábra). Mivel

A_{2} T_{1} = s - a_{2} = (a_{1} + a_{3} - a_{2}) / 2

és

M_{1} A_{2} = a_{1} / 2

, azért

\begin{matrix} M_{1} T_{1}^{2} = {(M_{1} A_{2} - A_{2} T_{1})}^{2} = \frac{{(a_{2} - a_{3})}^{2}}{4} . \end{matrix}

P

A_{1}

-ből induló belső szögfelezőnek és

a_{1}

-nek a metszéspontja, tehát

\begin{matrix} P A_{2} = \frac{a_{1} a_{3}}{a_{2} + a_{3}}, P A_{3} = \frac{a_{1} a_{2}}{a_{2} + a_{3}}, \\ P M_{1} = | M_{1} A_{2} - P A_{2} | = \frac{a_{1} | a_{2} - a_{3} |}{2 (a_{2} + a_{3})} . \end{matrix}

2. ábra

Végül a

P X M_{1}

és

P Q A_{2}

hasonló háromszögekből

\begin{matrix} M_{1} X : A_{2} Q = P M_{1} : P A_{2} = \frac{a_{1} | a_{2} - a_{3} |}{2 (a_{2} + a_{3})} \cdot \frac{a_{2} + a_{3}}{a_{1} a_{3}} = \frac{| a_{2} - a_{3} |}{2 a_{3}}, \end{matrix}

vagyis

\begin{matrix} M_{1} X \cdot M_{1} M_{2} = \frac{| a_{2} - a_{3} |}{2 a_{3}} \cdot A_{2} Q \cdot M_{1} M_{2} = \frac{{(a_{2} - a_{3})}^{2}}{2 a_{3}} \cdot \frac{a_{3}}{2} = M_{1} T_{1}^{2} . \end{matrix}

P Y M_{1}

és

P R A_{3}

hasonló háromszögekből pedig

\begin{matrix} M_{1} Y : A_{3} R = P M_{1} : P A_{3} = \frac{| a_{2} - a_{3} |}{2 a_{2}}, \end{matrix}

vagyis

\begin{matrix} M_{1} Y \cdot M_{1} M_{3} = \frac{| a_{2} - a_{3} |}{2 a_{2}} \cdot | a_{2} - a_{3} | \cdot \frac{a_{2}}{2} = M_{1} T_{1}^{2} . \end{matrix}

Ezzel a feladat állítását beláttuk, s azt is, hogy ez a közös pont éppen a beírt kör és a Feuerbach-kör érintési pontja.

Feladat: Tekintsük a következő tulajdonságú valós

(x_{n})

számsorozatokat:

x_{0} = 1

, és

i \geq 0

esetén

0 < x_{i + 1} < x_{i}

.
(a) Bizonyítandó, hogy minden ilyen sorozathoz van olyan

n \geq 1

, amelyre

\begin{matrix} \frac{x_{0}^{2}}{x_{1}} + \frac{x_{1}^{2}}{x_{2}} + ... + \frac{x_{n - 1}^{2}}{x_{n}} \geq 3, 999. \end{matrix}

(b) Adjunk meg egy ilyen sorozatot, amelyre minden

n

esetén

\begin{matrix} \frac{x_{0}^{2}}{x_{1}} + \frac{x_{1}^{2}}{x_{2}} + ... + \frac{x_{n - 1}^{2}}{x_{n}} < 4. \end{matrix}

Megoldás. Legyen

s = {x_{0}, x_{1}, ...}

egy megfelelő számsorozat, és legyen

\begin{matrix} S_{n} = \frac{x_{0}^{2}}{x_{1}} + \frac{x_{1}^{2}}{x_{2}} + ... + \frac{x_{n - 1}^{2}}{x_{n}} . \end{matrix}

Minden ilyen

s

sorozatra tekintsük azt az

s^{(1)} = {y_{0}, y_{1}, ...}

sorozatot, amelyet az

\begin{matrix} y_{i} = \frac{x_{i + 1}}{x_{1}}, i = 0,1,2, ... \end{matrix}

összefüggés definiál. Nyilvánvalóan

s^{(1)}

is megfelelő sorozat, azaz

y_{0} = 1

és

0 < y_{i + 1} < y_{i}

i \geq 0

esetén, továbbá

\begin{matrix} S_{n}^{(1)} & = \frac{y_{0}^{2}}{y_{1}} + \frac{y_{1}^{2}}{y_{2}} + ... + \frac{y_{n - 1}^{2}}{y_{n}} = \frac{1}{x_{1}} (\frac{x_{1}^{2}}{x_{2}} + \frac{x_{2}^{2}}{x_{3}} + ... + \frac{x_{n}^{2}}{x_{n + 1}}) = \\ = \frac{1}{x_{1}} (S_{n + 1} - \frac{x_{0}^{2}}{x_{1}}) = \frac{1}{x_{1}} (S_{n + 1} - \frac{1}{x_{1}}), \end{matrix}

hiszen

x_{0} = 1

.
Belátjuk, hogy a feladat (a) állítása nemcsak

3, 999

-re, hanem minden

4

-nél kisebb pozitív

a

számra teljesül. Valóban, tegyük fel, hogy mégis volna olyan megfelelő

s

számsorozat, melyre minden

n

-re

S_{n} < a

teljesül. Ekkor a fent definiált

s^{(1)}

sorozat olyan, hogy minden

n

-re

\begin{matrix} S_{n}^{(1)} = \frac{1}{x_{1}} (S_{n + 1} - \frac{1}{x_{1}}) < \frac{1}{x_{1}} (a - \frac{1}{x_{1}}) = \frac{a^{2}}{4} - {(\frac{a}{2} - \frac{1}{x_{1}})}^{2} ≦ 4 \cdot {(\frac{a}{4})}^{2} . \end{matrix}

s^{(1)}

-ből ugyanilyen módon képzett

s^{(2)}

sorozatra

\begin{matrix} S_{n}^{(2)} < \frac{{(a^{2} / 4)}^{2}}{4} = 4 \cdot {(\frac{a}{4})}^{4}, \end{matrix}

s általában ha az

s^{(k + 1)}

sorozatot a fenti mintára kapjuk az

s^{(k)}

sorozatból, akkor minden

n

-re

\begin{matrix} S_{n}^{(k + 1)} < \frac{1}{4} {(4 \cdot {(\frac{a}{4})}^{2^{k}})}^{2} = 4 \cdot {(\frac{a}{4})}^{2^{k + 1}} . \end{matrix}

Indirekt feltevésünk szerint

a < 4

, tehát

a / 4 < 1

, így a jobb oldal elég nagy

k

-ra kisebb

1

-nél. De ez lehetetlen, hiszen ha

s^{(k + 1)} = {z_{0}, z_{1}, ...}

, akkor például

\begin{matrix} S_{0}^{k + 1} = \frac{z_{0}^{2}}{z_{1}} = \frac{1}{z_{1}} > 1. \end{matrix}

Ezzel a feladat (a) állítását bebizonyítottuk.

Legyen most

s = {x_{0}, x_{1}, ...}

olyan megfelelő sorozat, melyre

S_{n} < 4

minden

n

-re. Az előbbieket

a = 4

-re alkalmazva kapjuk, hogy az

s^{(1)}

sorozatra

\begin{matrix} S_{n}^{(1)} < \frac{a^{2}}{4} - {(\frac{a}{2} - \frac{1}{x_{1}})}^{2} = 4 - {(2 - \frac{1}{x_{1}})}^{2} \end{matrix}

minden

n

-re. Az előbb láttuk, hogy

4 - {(2 - \frac{1}{x_{1}})}^{2} < 4

nem lehetséges, így

x_{1}

csak

1 / 2

lehet. Ekkor az

s^{(1)}

sorozat tagjai rendre

1

2 x_{2}

2 x_{3}

...

. Mivel az

s^{(1)}

sorozatra is igaz, hogy

S_{n}^{(1)} < 4

minden

n

-re, azért az

s^{(1)}

sorozat második tagja,

2 x_{2}

, csak

1 / 2

lehet. Ezért

x_{2} = 1 / 4

, és az

s^{(2)}

sorozatra, melynek tagjai így

1

4 x_{3}

4 x_{4}

...

S_{n}^{(2)} < 4

teljesül minden

n

-re. Ezt folytatva kapjuk, hogy ha van olyan megfelelő sorozat, mely teljesíti a feladat (b) részének feltételeit, akkor az csak az

1

1 / 2

1 / 4

...

1 / 2^{n}

...

sorozat lehet, ez pedig könnyen láthatóan jó. Így nemcsak megadtunk ilyen sorozatot, hanem azt is bizonyítottuk, hogy csak egy ilyen van.