Kezdőlap


Cím:	Szélsőértékek a körben
Szerző(k):	Kallós Károly
Füzet:	1984/január, 3 - 6. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vessünk fel egy igen egyszerű kérdést: a körvonal két pontját összekötő egyenes szakaszok közül melyik a leghosszabb? ‐ A kérdés olyan szorosan kötődik a szemlélethez, hogy a kisiskolás is tud rá válaszolni (1.ábra). Rajzoljunk most derékszögű töröttvonalakat a körbe; ezek közül melyik a leghosszabb? A két merőleges sugár együttes hossza (2. ábra) még nem ad maximumot, erről könnyen meggyőződhetünk (3. ábra). Amikor az $A C B$ töröttvonal hossza maximális, az $A B$ távolság a lehető legnagyobb (4. ábra). Ekkor a $C$ pont a kerületen van.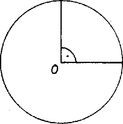

1. ábra

2. ábra

3. ábra

A C B

töröttvonal hossza egy derékszögű háromszög két befogójának az összege. Az 5. ábra jelölésével futtassuk

C

-nek az

A B

átmérőre eső (merőleges) vetületi pontját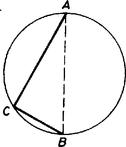

A

-ból

B

-be.

4. ábra

5. ábra

A középérték-tételek alapján

\begin{matrix} a + b = \sqrt[]{C' B \cdot A B} + \sqrt[]{C' A \cdot A B} = \sqrt[]{A B} (\sqrt[]{C' A} + \sqrt[]{C' B}) . \end{matrix}

Ez a kifejezés csak az

A C'

távolság függvénye, ha

r

adott. Mivel

A B

‐ és ezzel együtt

\sqrt[]{A B}

is ‐ állandó, az

a + b

és a

\sqrt[]{C' A} + \sqrt[]{C' B}

együtt növekszik, majd fogy, közben a maximumot

C' A - \frac{1}{2} A B

-nél éri el. A tételt ismerjük: adott átfogójú derékszögű háromszögek közül annak a kerülete maximális, amelynek egyenlők a befogói. Ekkor egyúttal a terület is maximális.
Nézzünk összetettebb problémákat is! Vegyünk fel a kör

A B

átmérőjén egy tetszőleges

C

pontot, majd az

A C

szakaszra

C

-ből mérjünk fel mindkét irányban

1 - 1 120^{\circ}

-os szöget. Ez a két szögszár a körvonalon kijelöli a

P

és

Q

pontot.

C

mely helyzetéhez tartozik az

A C + C P + C Q

szakaszösszeg legnagyobb értéke? (6. ábra.)

Miközben

C

az átmérőn vándorol, a kérdezett összeg eleinte növekszik, majd fogy. Máshogyan megfogalmazva: az

A C

növekedési üteme először felülmúlja a másik két szakasz együttes fogyási ütemét, majd ez megfordul. Előzetes vizsgálódás során legyen

C \equiv A

, ekkor a fenti összeg

2 r \sqrt[]{2}

. Ha pedig

C \equiv B

, akkor az összeg

2 r

. Több módon is igazolható, hogy a keresett szélső érték

A C = r

esetén alakul ki.
Lássunk egy változatot!

6. ábra

Legyen az ábra szerint

u

P

pont

P'

-vel j elölt vetületének távolsága a kör középpontjától. Pitagorasz tételéből kiindulva, a

60^{\circ}

-os derékszögű háromszögre támaszkodva felírjuk a

C P

szakaszt, majd kivonással az

A C

szakaszt is

u

függvényeként:

\begin{matrix} C P = \frac{2}{\sqrt[]{3}} \sqrt[]{r^{2} - u^{2}}; A C = r + u - \frac{\sqrt[]{r^{2} - u^{2}}}{\sqrt[]{3}}, 0 \leq u \leq r . \end{matrix}

Ebből

\begin{matrix} A C + C P + C Q = r + u - \frac{\sqrt[]{r^{2} - u^{2}}}{\sqrt[]{3}} + \frac{4 \sqrt[]{r^{2} - u^{2}}}{\sqrt[]{3}} . \end{matrix}

Ennek a szélsőértékhelye deriválással:

\begin{matrix} u = \frac{r}{2} (maximum) . \end{matrix}

A keresett összeg:

3 r

7. ábra

Legyen a következő feladatban

A C P ∢ = A C Q ∢ = 135^{\circ}

(7. ábra). Most

C

mely helyzetében lesz az előbbi

3

szakasz összege a legnagyobb? ‐ A számítás az előzőhöz hasonló. Jelöljük a szakaszösszeg-függvényt,

f

-fel:

\begin{matrix} f = r + u - \sqrt[]{r^{2} - u^{2}} + 2 \sqrt[]{2} \sqrt[]{r^{2} - u^{2}} = r + u + \sqrt[]{r^{2} - u^{2}} (2 \sqrt[]{2} - 1) . \end{matrix}

Ennek az

u

szerinti első differenciálhányadosát egyenlővé tesszük

0

-val, és az egyenletet

u

-ra megoldjuk. Az eredmény:

\begin{matrix} u = \frac{r}{\sqrt[]{10 - 4 \sqrt[]{2}}} \approx 0, 4798 r . \end{matrix}

Az eredményről leolvasható, hogy a

V

alakban terpeszkedő

2

egyenlő szakasz visszaszorítja az

A C

-t, így áll elő a maximum. Most

A C \approx 0, 6 r

.
Ennek ellenkezője következik be, ha

A C P ∢ = A C Q ∢ = 90^{\circ}

. Ekkor

u \approx 0, 4472 r

, vagyis

u

csökkent. Ha az

A C P ∢ = A C Q ∢

-et változtatjuk az értelmezési tartományban, az

u

értéke is változik. Érdekes feladat ennek a függvénykapcsolatnak a feltárása, megadása.
A problémasort elindító feladat többféleképpen általánosítható síkban és térben is. Tekintsünk csupán egy ilyen általánosított feladatot! ‐ Egy pontból kiinduló, párosával egyenlő szöget bezáró

4

félegyenes rendszerét hogyan helyezzük el egy gömbben, hogy a gömbbe eső szakaszok összege maximális legyen?
A megoldás logikai rendje a tárgyaltakéhoz hasonló. Az eredmény ‐ mint a szimmetriaviszonyok alapján várható ‐ a gömb középpontjából kiinduló

4

olyan sugár, melyben kettő-kettő mindig ugyanakkora szöget zár be egymással. Mekkora ez a szög? ‐ A szabályos tetraéder magasságpontjából a csúcsokba futó szakaszok hajlásszögéről van szó. Ez a szög kerekített értékben

109^{\circ} 28'

, pontosabban:

109, 4712^{\circ} ...

. A tárgyalt szögnek a természetben kitüntetett szerepe van, példaként említsük csupán a germánium-kristály rácsszerkezetét és a metán molekula térszerkezetét. (8. ábra).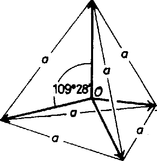

8. ábra

Vessük fel a következő kérdést: egy síkban fekvő, azonos pontból kiinduló félegyenesek közül a

2 - 2

szomszédos elem által bezárt szög legyen egyenlő. Hol, helyezzük el ezt a sugársort egy körben, ha azt akarjuk, hogy a körbe eső szakaszok összege maximális vagy éppen minimális legyen?
Az eredmény ismerős. Érdemes még egy percig itt időznünk, mert a feladat rokon egy alapvetően fontos tétellel: a körbe rajzolható

n

oldalú konvex sokszögek közül a szabályosnak a legnagyobb a kerülete, a körülírhatók közül pedig a szabályosé a legkisebb. A gömb szélsőérték tulajdonsága adja a választ arra a tréfás kérdésre, hogy miért nem szögletes a szappanbuborék. Az ismert tétel változatai a tankönyvekben és a versenyeken is helyet kapnak.